铜/铝磁脉冲半固态辅助钎焊界面扩散过程
2023-06-02余章钦胡建华杨正黄尚宇
余章钦,胡建华,杨正,黄尚宇
(武汉理工大学,武汉,430000)
0 序言
铜和铝具有良好的导电性和导热性,在电气和电子工业中应用广泛.将铜/铝及其合金连接形成可靠的复合结构,既可以实现结构轻量化,又能降低成本.铝和铜的熔点、线膨胀系数等性能存在差异,使其焊接较为困难.有学者研究铜铝异种金属的熔化焊、固相焊及超声焊接,发现存在金属间化合物和氧化颗粒残留等缺陷[1-4].磁脉冲半固态辅助钎焊工艺[5]结合电磁成形、半固态成形和钎焊的优点,利用洛伦兹力驱动母材挤压半固态钎料使其产生强烈的剪切流动,破坏并去除氧化膜,细化钎缝组织[6],提高焊接接头的综合性能.王振东等人[7]研究了Zn-15Al 钎料的固相率对钎焊接头的影响,结果发现,固相率为60%的界面结合情况较好.黄海川等人[8]研究了放电电压对钎焊的影响,研究表明,第二次放电电压为7 kV 时能实现良好的冶金结合,且铝侧形成α-Al 和CuZn5金属间化合物,钎料层出现α-Al、富锌相及CuZn5,铜侧形成锯齿状扩散层.高远等人[6]研究温度条件对铜/铝磁脉冲半固态钎焊的影响,结果发现,温度升高会导致α相形状变得不规则,并且会有粗大树枝状组织产生的倾向,同时钎缝中铜含量升高.邓凌波等人[9]研究了铜/铝管磁脉冲半固态钎焊钎料的流变行为,发现带锥角集磁器能有效细化铜/铝接头搭接区域中部钎缝组织,并最终提高钎焊接头的抗剪强度.
目前关于铜/铝磁脉冲钎焊的研究侧重于工艺优化、钎料优化、钎缝组织及连接强度的研究,而分子动力学(molecular dynamics,MD)在研究结构演化和微观扩散机制方面有一定优势[10].Zhang 等人[11]借助MD 分别研究了6061 铝合金与AZ31B 镁合金爆炸焊中冲击速度和冲击角度对扩散系数的影响,结果表明,碰撞角保持不变时,扩散系数随着碰撞速度的增大呈线性增大;碰撞速度保持440 m/s不变时,扩散系数随着碰撞角的减小呈线性减小.Chen 等人[12]利用MD 研究铜/铝爆炸焊,结果表明,当未加横向速度时,扩散系数与纵向速度成正比.当纵向速度固定时,扩散系数与横向速度的平方成正比.Zhang 等人[13]利用MD 研究不锈钢和纯镍的扩散焊过程中原子的扩散行为,结果表明,表面粗糙度对扩散行为有显著影响,并且扩散焊的压力效应小于温度效应.Mao 等人[14]利用MD 研究铜/铝固液界面原子的扩散行为,研究表明,Cu 原子的扩散深度与体系温度呈线性关系,扩散层厚度与扩散焊时间呈抛物线关系.Yang,Ma 和Samanta等人[10,15-16]利用MD 研究铜/铝超声波焊接中焊缝的动态演变,以及温度、压力和超声波速度对铜/铝扩散的影响,结果表明,在超声波焊接中铜/铝出现了不对称扩散,扩散层厚度随焊接时间的延长而增加.袁晓静等人[17]采用MD 对微弧等离子增材制造NiCr 合金构件生长过程中温度场变化及等轴晶生长过程进行模拟,研究表明,冷却速率为3.38 K/ps 和0.675 K/ps 时,Ni-Cr 体系呈现非晶凝固,冷却速率0.077 5 K/ps 下,Ni-Cr 体系自发形核长大.
通过建立的铜-钎料-铝体系的MD 模型,模拟铜/铝磁脉冲半固态钎焊过程原子的扩散行为,研究了不同冲击速度对冶金结合扩散层厚度的影响,找到了模拟扩散层厚度与试验扩散层厚度之间的关系.
1 试验和模拟方法
1.1 试验方法
采用的试验材料为T2 紫铜、Zn15Al 和1060铝合金,其中1060 铝合金为退火态,试验材料化学成分如表1 所示.Zn-15Al 钎料在固相率为60%时可以实现较好的焊接效果[7],故焊接试验在410 ℃(对应固相率为60%)下进行.

表1 试验材料的化学成分(质量分数,%)Table 1 Chemical compositions of experimental materials
放电设备使用WG-IV60kJ 型磁脉冲成形机,最大充电电压为11 kV,试验电容为550 μF.试验工装主要由磁脉冲成形线圈、集磁器、感应加热线圈、热电偶、外管、钎料和内管组成,如图1 所示.工艺过程有两次放电过程(图2),一是初装定位管件后,在常温条件下通过脉冲放电产生的电磁力对内、外管和钎料进行装夹;二是设备充电后再通过感应线圈加热,当钎料温度达到410 ℃时,停止加热并放电,在室温下冷却,获得铜/铝管接头试样.

图1 工装示意图Fig.1 Tooling diagram.(a) tooling model;(b) actual tooling
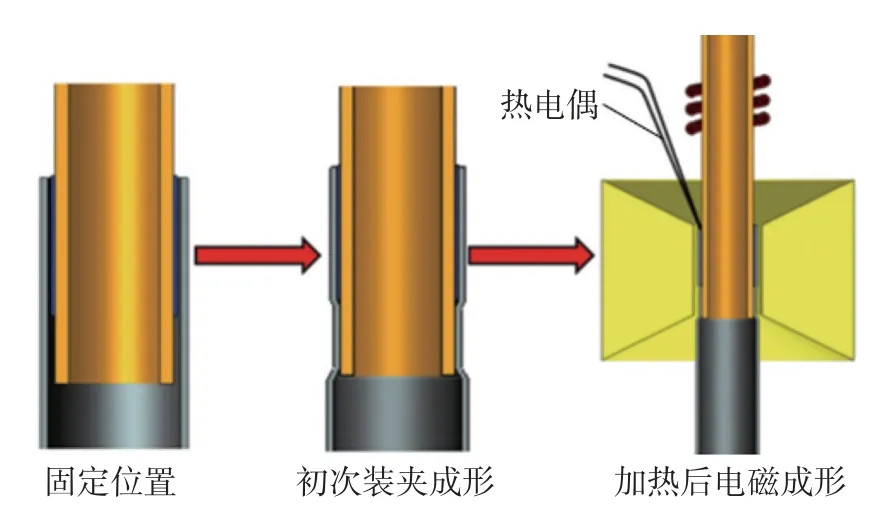
图2 工艺过程Fig.2 Technological process
1.2 模拟过程
MD 模型使用LAMMPS 软件进行模拟.模拟模型由铝基体、Zn15Al 钎料和铜基体组成,如图3 所示.构建3 个不同的区域,左中右3 层(z方向)分别放置铝原子、钎料原子和铜原子.铝和铜都是体心立方晶格,铝和铜的晶格常数分别为4.05 Å和3.67 Å;钎料层以锌的密排六方构型为基础随机将33%的Zn 原子替换成Al 原子,晶格常数为2.67 Å,模拟Zn15Al 钎料.模拟体系x,y和z方向分别对应[100],[010]和[001]晶向,尺寸为2.2 nm × 2.2 nm × 34 nm,其中铝、钎料和铜区域的长度均为10 nm,铝、钎料和铜区域创建的原子数分别为3 025,4 725 个和4 725 个.3 个区域放在同一个模拟盒子,其中铝和钎料、钎料和铜的冲击接触面之间距离均为2 nm.x和y方向设置为周期边界条件;在冲击方向(z方向)上,铝区域的最左端和铜区域的最右端各取10 Å 距离的原子作为固定边界,固定边界原子在整个模拟过程中不受力的作用.模拟选用的势函数是采用Dickel 等人[18]拟合的MgAlZn 的meam 势函数、Liu 等人[19]开发的CuAl 的EAM 势函数和苏文辉等人[20]开发拟合的CuZn 的Morse 势函数参数.系统温度为300 K,时间为30 ps 的NVT 系综进行弛豫,使模拟体系初始化.整个模拟体系是金属体系,所以选择0.001 ps作为体系的时间步长.升温后在模拟冲击钎焊过程中,铜侧边界固定以防止模拟中体系发生移动,在铝侧边界向右施加不同的速度,模拟不同电压下的冲击钎焊.

图3 分子动力学模拟初始模型(nm)Fig.3 Initial model of molecular dynamics simulation
初始化后使用NPT 系综,将x和y方向上的压强设置为1.01 × 105Pa,压力调节阻尼系数(pdamp 系数)设置为0.1,可以更快的稳定体系压强.将体系的温度从300 K 升高至770 K(此时钎料模拟体系的固相率为60%),对铝侧边界原子施加不同的冲击速度,使用NVE 系综来计算体系的运动,冲击时间为100 ps,去除铝侧边界原子的运动速度,并继续使用NVE 系综模拟冲击后的钎焊扩散混合过程.当NVE 系综的温度达到稳定则表示混合过程结束,混合模拟时间为1 000 ps.钎焊过程中各原子的运动情况均可在OVITO 软件中观察到,从而揭示了钎焊界面各原子混合的机理,为在试验中得到更好的钎焊接头提供理论指导.
2 模拟结果与分析
2.1 无冲击时原子分布
图4 为无冲击速度情况下铝基体/钎料界面扩散过程中运动最远的原子位置变化曲线.在没有冲击的情况下,扩散界面中Al,Zn 和Cu 原子的移动驱动力理论上差距不大,但实际上各个原子的移动表现并不同.从图4 可以看出,初始阶段原子移动很快,随着体系逐渐平衡,移动速度降低,最后在一个位置震动.图中铝基体原子运动的最远距离为0.6 nm,而钎料中Al 原子和Zn 原子运动最远距离分别为1.6 和1.4 nm.钎料中Zn 原子和Al 原子的运动距离远大于铝基体中的Al 原子,铝基体和钎料中的Zn 原子和Al 原子随着边界上原子排列无序区域的增加而扩散混合,说明钎料的无序化程度比铝基体无序化程度更大.
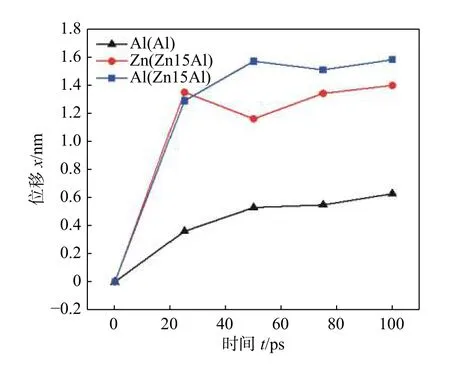
图4 铝基体和钎料中位移最远原子的位移变化Fig.4 Displacement variation of the furthest displaced atom in aluminum matrix and solder
2.2 不同冲击速度原子分布
2.2.1 界面原子位形
图5 为不同冲击速度下在NVE 系综仿真进行到100 ps 时原子位形图.从图5a 可以看出,铝基体与钎料的结合界面有明显的相互扩散混合,而铜基体与钎料的结合界面未发现明显的原子相互扩散.随着冲击速度的增加,钎料和铝基体原子进一步相互扩散,铝基体和钎料之间的扩散层厚度也随之增加;铜基体与钎料之间也发生轻微的相互扩散,在冲击速度100 m/s 下,模拟扩散层最厚为0.6 nm 左右.同时发现,铝基体原子与钎料原子发生混合时,钎料中的Zn 原子和Al 原子向无序排列的铝基体中的运动趋势更加明显.而铝基体原子进入扩散层后向钎料中的扩散较为困难,铝基体原子的运动的最远位置离平衡位置不到1 nm,运动距离非常短.
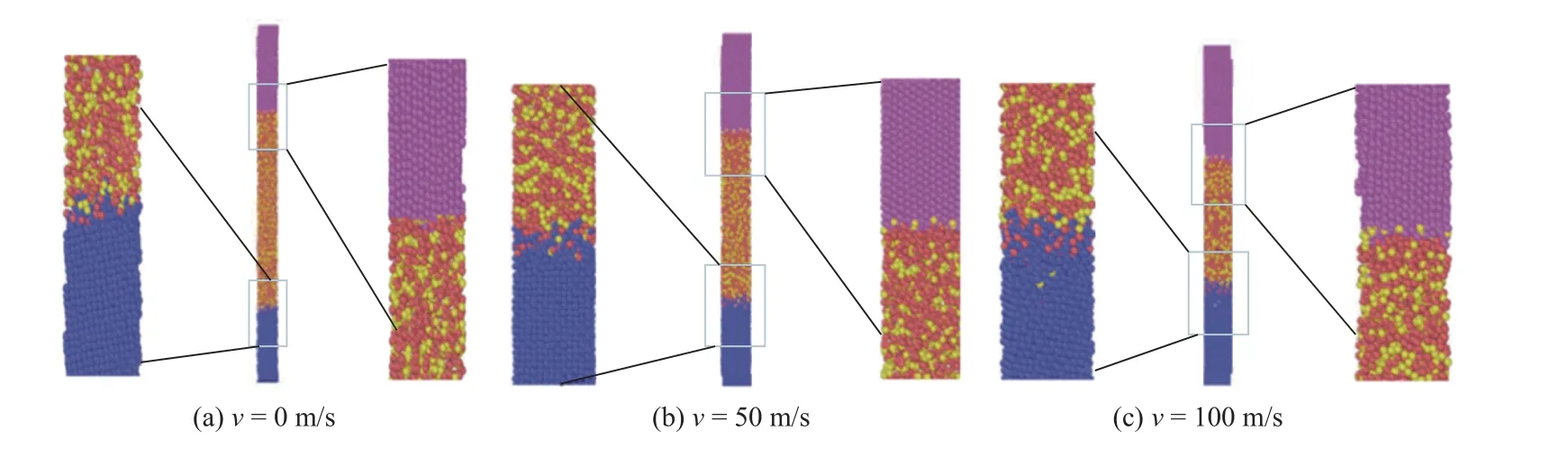
图5 不同冲击速度下原子位形图Fig.5 Shape and position of atoms under different impact velocity.(a) v=0 m/s;(b) v=50 m/s;(c) v=100 m/s
为了更清楚地了解界面扩散行为,采用NVE系综模拟了冲击速度100 m/s 下模拟体系中各原子随时间的位形变化.图6 为模拟体系各原子在0,500 ps 和1 000 ps 时刻的原子位形图.开始阶段,钎料中仅有少量的Zn 和Al 原子向铝基体和铜基体扩散;随着扩散过程的进行,更多的Zn 原子和Al 原子从钎料中扩散至铜基体和铝基体.在NVE 系综模拟的最终时刻,铝基体和钎料界面形成了Zn 和Al 元素相互混合且较厚的扩散层,铜基体和钎料的界面处形成较薄的扩散层.
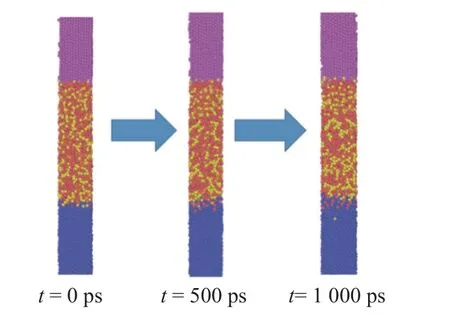
图6 不同时刻的原子位形Fig.6 Shape and position of atoms at different moment
2.2.2 界面原子含量
利用NVE 系综分别模拟冲击速度分别为0,50,60,70,80 m/s 和100 m/s,冲击时间为100 ps时,铝基体侧界面附近的原子含量情况,模拟计算到1 000 ps 时的分布曲线如图7 所示.随着冲击速度的增大,界面处原子含量变化趋势逐渐缓和过渡,界面扩散层厚度也不断增加.
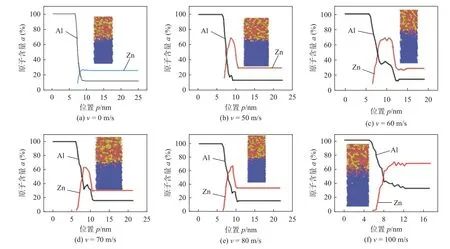
图7 从铝基体至钎料界面扩散层原子含量分布Fig.7 Atom content distribution in the diffusion layer from aluminum matrix to solder interface.(a) v=0 m/s;(b) v=50 m/s;(c) v=60 m/s;(d) v=70 m/s;(e)v=80 m/s;(f) v=100 m/s
图7 中Zn 原子和Al 原子的含量分布曲线的交点更靠近钎料侧,说明铝基体原子和钎料含有的锌原子铝原子的相互混合主要发生在铝基体侧.为了研究其原因,利用NVE 系综模拟冲击速度80 m/s下不同时刻下原子含量分布,如图8 所示.开始时,交点靠近钎料一侧,进一步验证了钎料原子向铝基体扩散速度大于铝原子向钎料扩散速度.但随着时间增加,交点位置向铝基体侧移动,直至达到中间位置附近,这是铝基体原子向钎料扩散比例不断提高的结果.从图8a 和图8b 可以看出,Zn 和Al 含量变化的区间宽度有明显增大,而从图8b~图8e 可以发现,Zn 和Al 原子扩散层厚度基本没有变化,这说明原子在模拟初期时扩散较快,随后达到稳定,扩散速度降低.而铜侧则是陡变的曲线,可以判断出在冲击速度为80 m/s、冲击时间为100 ps 和模拟时间为1 000 ps 时,铜侧未形成稳定的界面扩散层.
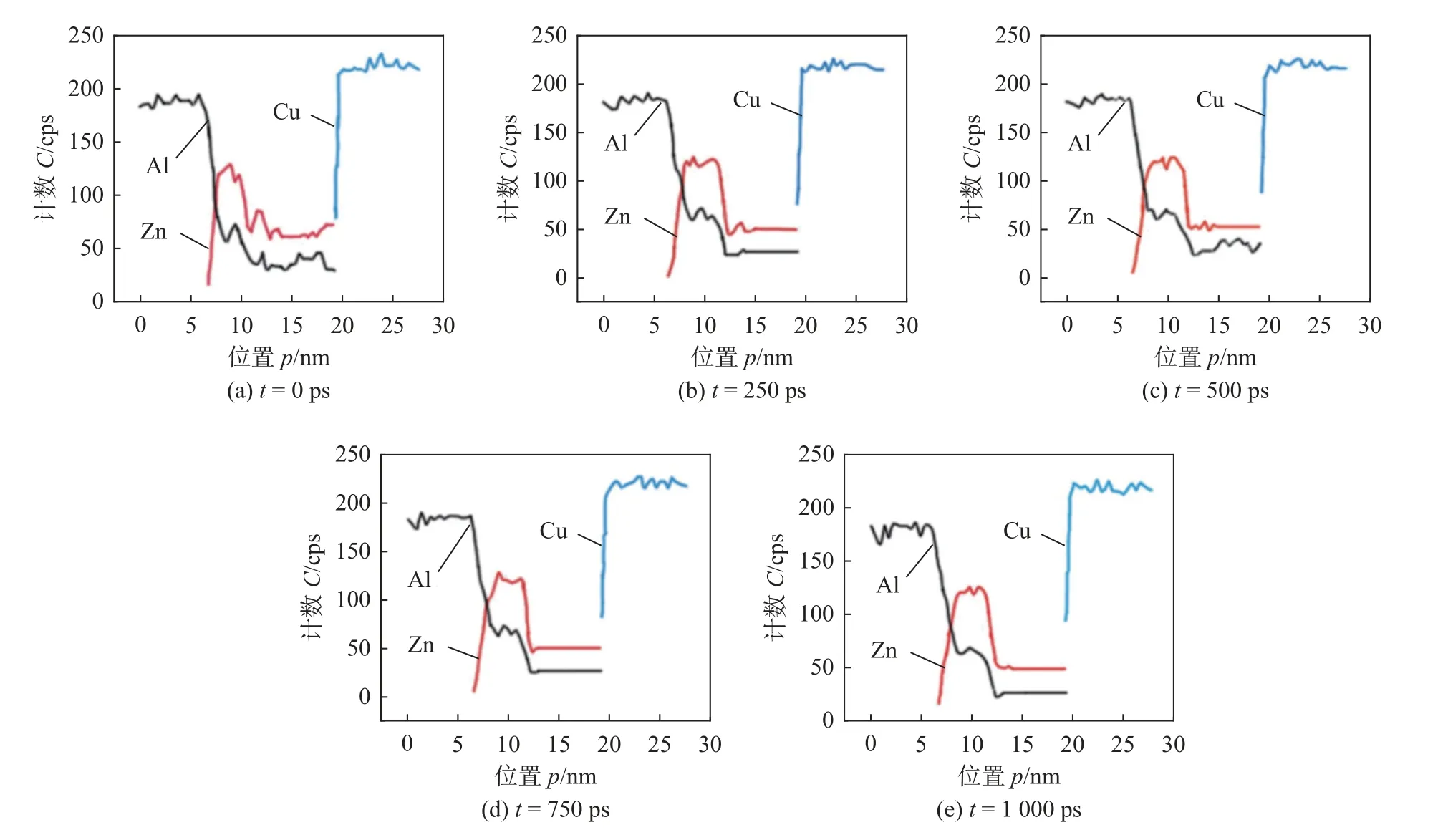
图8 冲击速度80 m/s 下不同时刻的原子含量分布Fig.8 Atomic content distribution at different times when the impact speed of 80 m/s.(a) t=0 ps;(b) t=250 ps;(c) t=500 ps;(d) t=750 ps;(e) t=1 000 ps
3 试验结果与分析
图9 和图10 分别为冲击速度分别为57,61,67,71 m/s 和75 m/s 焊接接头的微观形貌和能谱分析图.能谱扫描点从钎料开始逐渐进入界面层和铝基体.进入界面过渡层后,Al 元素含量单调增加直到100%(即完全进入铝基体),而Zn 元素含量单调递减直到0.不同冲击速度57,61,67,71 m/s 和75 m/s 下原子含量梯度变化的扩散层厚度分别为3.5,3.8,4.5,5.1 μm 和5.6 μm,说明随着冲击速度增加,扩散层厚度随之增加.
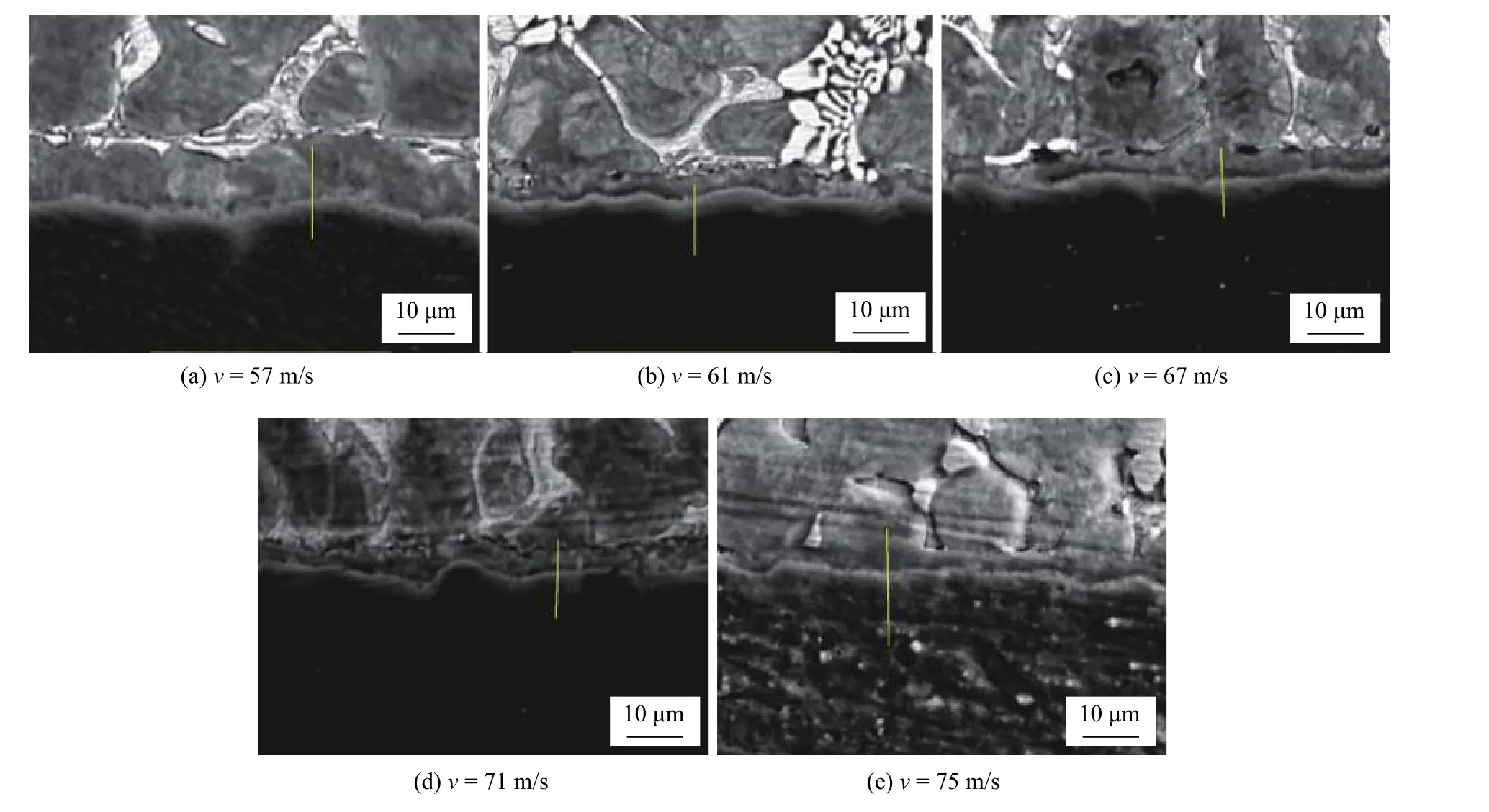
图9 不同冲击速度下铝侧界面微观组织Fig.9 Microstructure of aluminum side interface at different impact speeds.(a) v=57 m/s;(b) v=61 m/s;(c) v=67 m/s;(d) v=71 m/s;(e) v=75 m/s
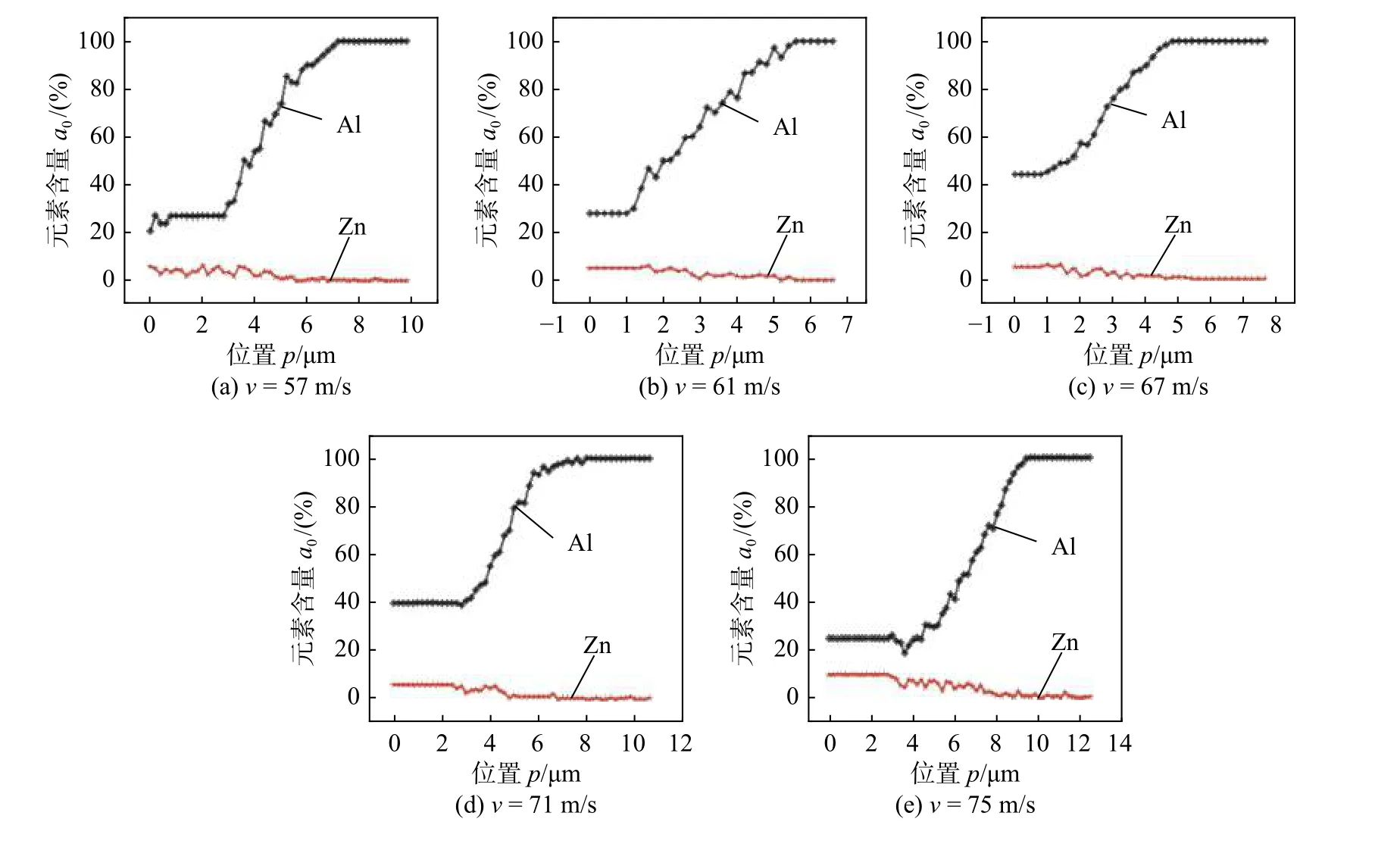
图10 不同冲击速度下铝侧界面EDS 曲线Fig.10 EDS curves of aluminum side interface at different impact speeds.(a) v=57 m/s;(b) v=61 m/s;(c) v=67 m/s;(d) v=71 m/s;(e) v=75 m/s
图11 和图12 分别为不同放电电压下钎焊时铜基体与钎料结合界面处的微观形貌和EDS 曲线,能谱扫描点从铜基体开始逐渐进入界面层和钎料.Cu 元素含量从100%降到60%左右,Zn 元素从0 增加到20%左右,Al 元素含量从0 增加到30%左右.不同放电电压0,4.5,5.0,5.5 kV 和6.0 kV 下扩散层厚度分别为1.9,1.8,2.0 μm 和2.5 μm.在一定的速度范围内,钎料和铜基体之间的相互扩散受冲击速度影响不大.从EDS 曲线可以看到,在界面扩散层中,铜含量的分布规律与铝、锌有区别,这与铜、锌在扩散混合过程中形成了铜锌化合物有关.

图11 不同放电电压下铜侧界面微观形貌Fig.11 Microstructure of the aluminum side interface at different discharge voltages.(a) U=4.0 kV;(b) U=4.5 kV;(c)U=5.0 kV;(d) U=5.5 kV;(e) U=6.0 kV
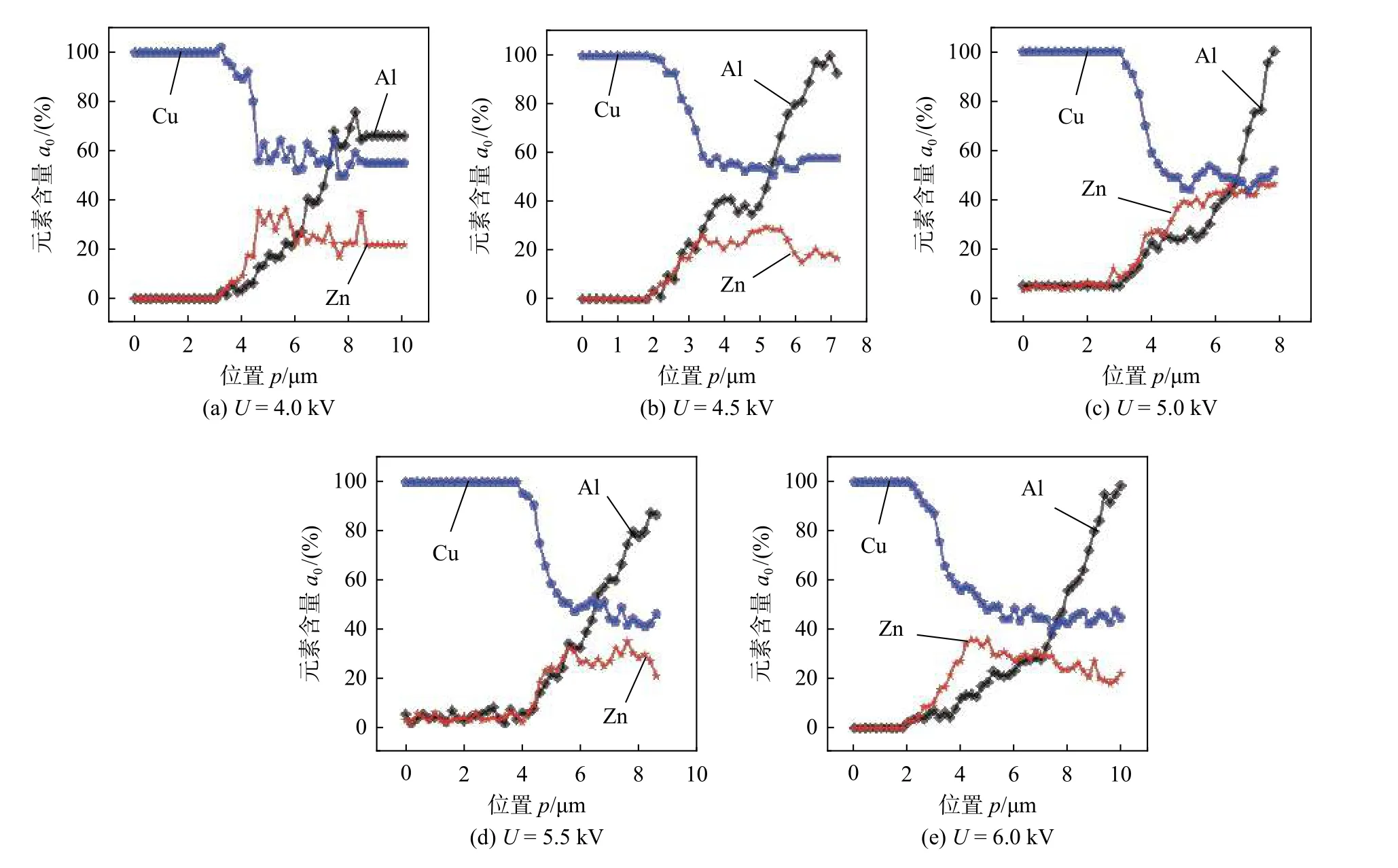
图12 不同放电电压下铜侧界面EDS 曲线Fig.12 EDS curves of copper side interface at different discharge voltages.(a) U=4.0 kV;(b) U=4.5 kV;(c) U=5.0 kV;(d) U=5.5 kV;(e) U=6.0 kV
为了获得模拟结果与试验结果之间的关系,对模拟得到的界面扩散层厚度和试验得到的界面扩散层厚度一一对应.由于模拟时铜侧未形成明显的界面扩散层,这里主要分析钎料和铝基体侧的界面扩散层厚度变化.图13 为铝侧界面扩散层厚度和冲击速度的关系.图13 中显示扩散层厚度随冲击速度的变化接近一条直线,说明界面扩散层厚度与冲击速度成线性关系,在冲击速度为57,61,67,71 m/s 和75 m/s 下模拟所得的界面扩散层厚度分别为1.475,1.575,1.725,1.825 μm 和1.925 μm.用上述模拟计算出的铝基体侧界面扩散层厚度与在相同冲击速度下试验得到的铝基体侧界面扩散层厚度作出对应的关系.从图14 可以看出,模拟的铝侧界面扩散层厚度与试验得到的铝侧界面扩散层厚度可拟合成线性关系.若将不同冲击速度下模拟得到的界面扩散层厚度代入此曲线即可预测试验扩散层厚度,如表2 所示,试验与模拟预测结果最大误差为2.8%,说明用模拟方法能较好地预测试验扩散层厚度.
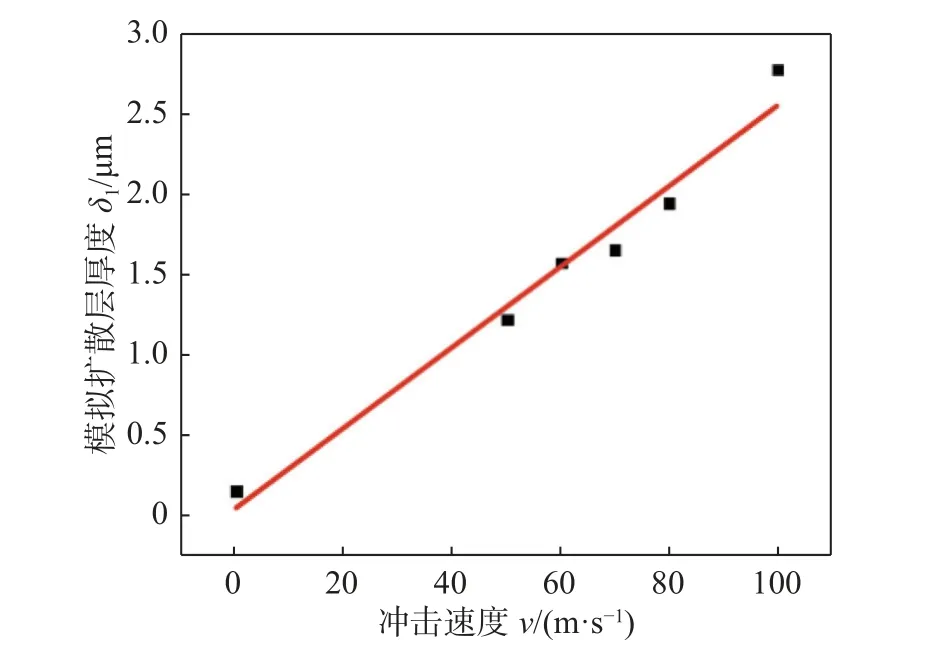
图13 不同冲击速度下铝侧界面模拟扩散层厚度Fig.13 Simulated diffusion layer thickness of interface at aluminum side under different impact speeds
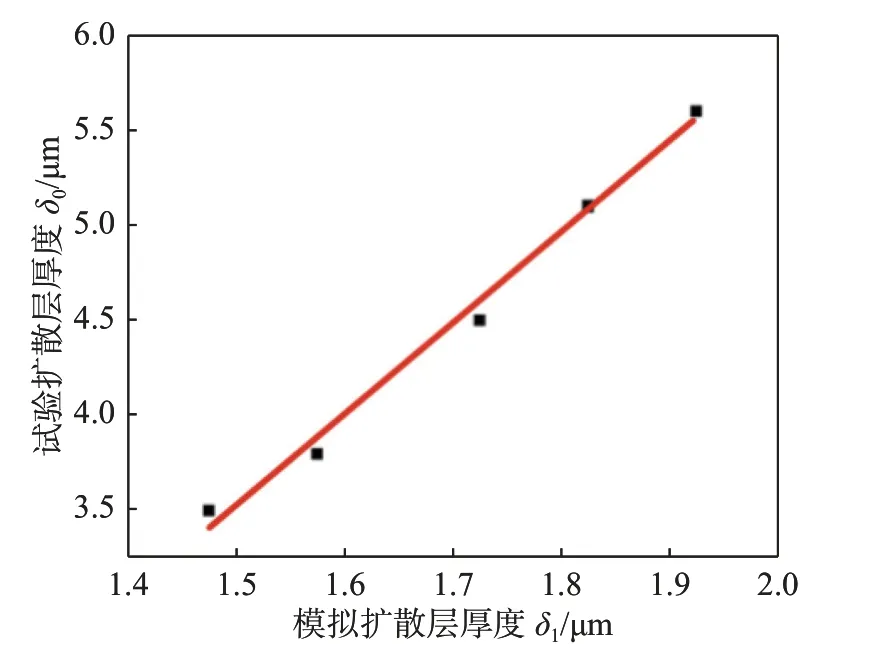
图14 模拟扩散层厚度与试验扩散层厚度的关系Fig.14 Relationship between the simulated thickness of the diffusion layer and the measured thickness in the experiment
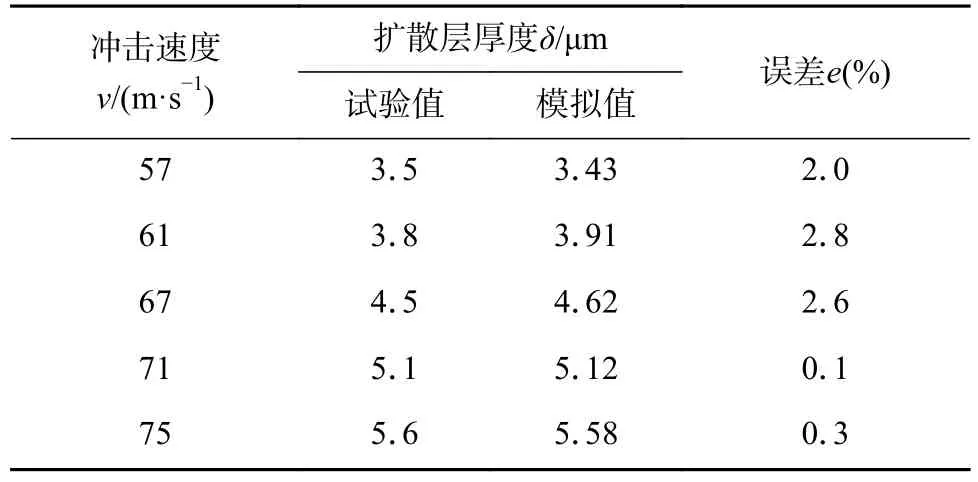
表2 不同冲击速度下界面模拟和试验扩散层厚度Table 2 Simulation and experimental diffusion layer thickness of interface under different impact speeds
4 结论
(1) 在温度为770 K、无冲击的情况下,钎料中的原子进入铝基体侧的界面扩散层后扩散容易;而铝基体原子进入界面扩散层后向钎料中扩散较为困难.
(2) 随着冲击速度从57~ 75 m/s 不断增大,铝侧模拟和试验扩散层厚度不断增加;而铜侧模拟扩散层厚度增加不明显,试验中铜侧界面扩散层厚度稳定在 2 μm 左右,说明冲击速度对其影响相对较小,界面上无序排列的原子较少,故界面扩散层厚度较小.
(3)根据模拟的情况,建立了在相同放电电压下模拟的界面扩散层厚度和试验界面扩散层厚度之间的关系,由模拟计算出的界面扩散层厚度与试验界面扩散层厚度相比较,最大误差为2.8%.
