基于载波相位观测的无人机集群相对定位方法*

2023-06-01潘礼规尹佳琪徐春光

中山大学学报(自然科学版)(中英文) 2023年3期

潘礼规，尹佳琪，徐春光

1.中山大学航空航天学院，广东深圳 518107

2.中国航天科工信息技术研究院，北京 100144

无人机集群编队是无人机应用的新模式，在执行任务过程中，集群飞行具有诸多优势，已经成为无人机领域的研究热点（樊琼剑等，2009；宗群等，2017）。目前，集群编队研究主要集中在编队飞行控制策略（Lau et al.，2015；王祥科等，2021）、紧密编队气动影响（詹光等，2019）、编队相对位置保持（彭建帅等，2021）与变换（Richert et al.，2013）以及编队航迹规划（Shorakaei et al.，2014；Zhang et al.，2015）等几个方面。对军用无人机而言，无人机集群作战模式是未来发展方向之一，相比于单机作战，集群作战具有低可探测性、协同作战、饱和攻击以及低成本等优势（蔡杰等，2020）。此种作战模式需具备良好的协同交互能力，协同导航是其中的关键之一。无人机协同导航指无人机编队间通过机间数据链的信息交互，对原有导航信息进行融合校准，以提高集群整体的导航精度（许晓伟等，2017）。此外，无人机间的高精度相对定位与导航技术是实现协同导航的重要条件，为无人机集群编队飞行提供了基础保障。为弥补传统导航系统的缺陷，有相关学者进行了多方面研究。

熊骏等（2018）研究了基于UWB辅助的相对导航方法，结果表明仅依靠较少GPS卫星即可达到较好的相对导航精度。刘晓洋等（2019b）和谷旭平等（2021）研究了分层式协同导航方案，该方案改善了传统主从式无人机协同导航的性能，一定程度上校正了低精度的INS 误差。王念曾等（2019）将UWB 测距融入到INS/GNSS的相对导航算法中，使小型无人机的定位精度达到了厘米量级。Xu等（2020）则研究了INS/Vis‐Nav/UWB 的分布式融合算法，同样可获得厘米级的相对估计精度。潘瑞鸿等（2017）利用两无人机间的测距测角信息，构建了以UAV 为顶点的三角构型，仿真结果表明：该方法获得的导航精度高于航位推算，且误差不随时间累积。刘晓洋等（2019a）提出了基于测距/测速的协同导航算法，利用扩展卡尔曼滤波估计僚机的状态误差，结果表明：相比于单INS和仅测距的方案，该方法能够获得更高的估计精度。无人机姿态信息可通过INS 获得，通过两架无人机进行差分处理可得到相对姿态信息，但其误差随时间推移而发散，利用相对观测来解算无人机姿态信息的研究较少，而姿态对于无人机集群协同控制同样至关重要。因此，在无人机集群的协同定位中，同时实现位置、速度和姿态信息的状态估计显得尤为重要。

针对无人机集群的协同定位问题，提出了一种新的相对定位技术，通过引入短距离小功率的无线电发射/接收装置，利用载波相位观测量建立一种机间相对观测模型，同步解算集群内无人机的位置、速度和姿态。该方法仅依靠机间测距就可估计出某一无人机相对于另一无人机的位置姿态及其速率状态信息，而无需进行测速测角，在一定程度上降低了导航传感器的成本，同时也简化了传感器的数学模型，对提高无人机集群协同控制能力具有较高的研究和应用价值。

1 相对导航系统设计

1.1 相对导航方案

设计的相对导航方案采用主从式导航方式，每架无人机机身上均配备3 个天线，3 个天线构成一定的三角几何关系，根据此特性可构建一个与无人机机体固连的基准坐标系，如图1所示。

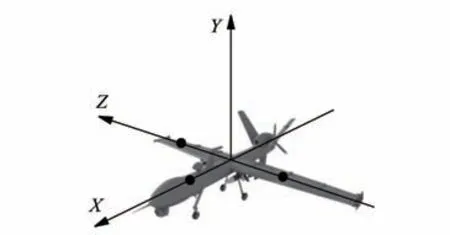
图1 天线安装示意图Fig.1 Schematic diagram of antenna configuration

每架无人机相同位置的天线均能够发射相同频率的电磁波，且不同位置的天线可发射不同频率的电磁波，即每架无人机都能够发射3种点频的电波。同时，每架无人机的每个天线均可实时检测到领航无人机发射的3个点频电波相位。

无人机集群编队飞行时，仅由领航无人机发射3种点频电波，而其他无人机均实时检测主机发出的3个点频信号到达本机每个天线的相位值。因此，针对主从两架无人机而言，从无人机的每个天线位置均可检测到领航无人机3个天线所发出的电磁波相位值，即每架从机均可在任意时刻获得9个相位测量值。根据这9个相位值，可分别解算出该从飞行器相对于领航无人机机体坐标系的相对位置与姿态，从而得到相对运动导航参数。

以某一领航无人机的机体坐标系作为导航坐标系，将主从式结构设计成2种方案：1MA-1FA和3MA-1FA 方案。其中，1MA-1FA 表示一架主飞行器（MA，master aircraft）对一架从飞行器（FA，follower aircraft）的观测模型（见图2（a）），3MA-1FA 表示3 架主飞行器（MA）对一架从飞行器（FA）（见图2（b））。进而，根据主飞行器疏密布局方式布置成两种情况，以研究疏密分布情况对定位性能的影响。

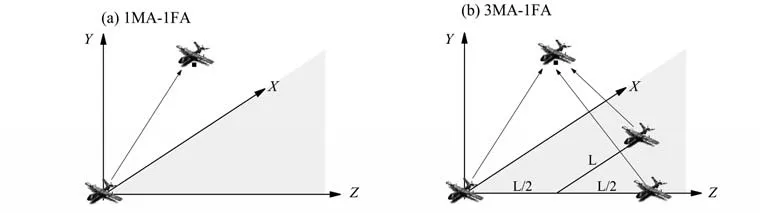
图2 主-从飞行器观测示意图Fig.2 Diagram of master aircraft observing follower aircraft

若领航无人机出现故障无法承担电波发射任务，则按预先指定的顺序，由下一顺位无人机接替领航任务，从而保证导航过程的连续性。

1.2 相对导航模型

1.2.1 基本位置模型以某一领航无人机机体坐标系作为导航坐标系，则可得领航无人机机身上的3 个天线位置分别为(a，0，0)、(0，0，b)和(0，0，−b)，且其3 个天线发射的电磁波波长分别记为λ1、λ2、λ3。记任意非领航无人机机体坐标系在导航坐标系中的位置为(x，y，z)，且该无人机机体坐标系相对于导航坐标系的姿态角分别记为方位角ψ、俯仰角ϑ和滚动角γ。定义导航坐标系至非领航无人机机体坐标系的旋转矩阵由欧拉角表示，即先绕Y轴旋转方位角ψ，再绕Z轴旋转俯仰角ϑ，最后绕X轴旋转滚动角γ计算。若已知非领航无人机机体坐标系原点在导航坐标系中的相对位置(x，y，z)，则非领航无人机机背上的3 个天线在导航坐标系中的位置为

式中旋转矩阵C表示领航无人机机体坐标系到其他无人机机体坐标系的转换矩阵

其转置即CT则表示其他无人机机体坐标系至领航无人机机体坐标系的转换矩阵。

将式（2）代入式（1），得非领航无人机3个天线的位置为

记领航无人机上的3 个天线在其导航坐标系中的位置为（xi0，yi0，zi0），其中i表示领航无人机上的第i个天线，且i= 1，2，3，其位置坐标为

根据式（3）与（4），可得领航无人机上的第i个天线与其他无人机上第j个天线之间的距离rij为

式中j表示非领航无人机上的第j个天线，且j= 1，2，3.

记领航无人机上的天线i发出的电波到其他无人机上天线j的相位角为θij，则在一个测量周期内，领航无人机上的3 个天线到非领航无人机上的3 个天线共9 个相位角可记为（θi1，θi2，θi3）.另外，相位角、波长与距离之间的关系为

1.2.2 基本速度模型假设无人机的相位测量周期为T，且领航无人机上的第i个天线发射的电磁波到达其他无人机上的第j个天线的相位测量值为θij。若当前时刻记为t0，且当前时刻t0之前的第k个测量周期节点获得的相位测量值为θijk，则可通过选择合适的测量周期T来保证连续周期节点间的相位测量值之差δθijk=（θijk−θij(k+1)），k= 0，1，2，…，N，维持在(−π，π)的范围内。因此，天线间的相对速度值为

式中N表示当前时刻之前的第N个测量周期节点。

根据式（3）给出的非领航无人机上3 个天线的位置与自身机体坐标系原点以及姿态角的关系表达式，其两边对时间求一阶导，可得相对速度与机体坐标系的原点速度以及姿态角变化率的关系为

式中C1、C2表示式（3）中相应向量对姿态角速率的Jacobian矩阵，且

根据式（5）给出的领航无人机上的第i个天线与非领航无人机上的第j个天线间的距离表达式，其两边对时间求导可得相对速度为

联合基本位置方程与基本速度方程，可求解任意非领航无人机机身上3个天线的位置与速度参数，进而得到无人机机体坐标系的位置及其姿态参数。

取基本位置速度模型的非线性向量方程为

式中Z表示观测向量；h(X)表示非线性向量函数。

若观测量取Z=[ri1ri2ri3ṙi1ṙi2ṙi3]T，则基本位置速度关系方程为

式中v为观测模型噪声，满足均值为零的高斯白噪声序列。

2 扩展卡尔曼滤波算法

扩展卡尔曼滤波算法根据状态向量最优估计值对状态方程和观测方程做泰勒近似并保留一阶项，将状态方程和观测方程线性化处理（秦永元等，2015）。

2.1 状态方程

非领航无人机在导航坐标系中的离散时间状态方程为

式中Xk表示系统状态向量，利用非领航无人机在k时刻3 个天线的位置、速度进行描述，即Xk=[x1x2x3ẋ1ẋ2ẋ3]T，其中xj=［xj yj zj］T，ẋj=［ẋj ẏj żj］T，j= 1，2，3；f[⋅]表示非线性状态向量函数；wk表示系统模型噪声，满足均值为0的高斯白噪声序列，其统计特性为

式中Qk表示过程噪声方差矩阵；δk，j表示克罗内克δ函数。

假设已知系统在tk−1时刻的系统状态参数最优估计值X̂k−1和估计值的协方差矩阵Pk−1。将式（9）的离散时间状态方程在系统状态X̂k−1值处进行泰勒近似，忽略二阶以上的高阶项，得

式中X̂k−1表示tk−1时刻非领航无人机状态参数的最优估计值。

令

则有

2.2 观测方程

与状态方程类似，扩展卡尔曼滤波的非线性观测方程是在状态方程得到的一步预测值X̂k|k−1处进行泰勒近似，并仅保留线性项，从而将非线性问题进行线性化处理。

非领航无人机在导航坐标系中的离散时间观测方程为

式中Zk为系统观测向量，利用k时刻主飞行器对从飞行器的相位量测值表示，即Zk=[ri1ri2ri3ṙi1ṙi2ṙi3]T；h[⋅]表示非线性向量函数；vk表示系统观测噪声，满足均值为零的高斯白噪声序列。

假设已获得系统在tk时刻的状态一步预测值X̂k|k−1和预测值的协方差矩阵Pk|k−1。将式（12）的离散时间观测方程在模型预测值X̂k|k−1处进行泰勒展开，仅保留一阶线性项，得

式中X̂k|k−1为系统状态量的一步预测值。

令

则有

上述简要推导了非线性状态方程与非线性观测方程进行线性化处理的过程，因为上一历元的状态最优估计值X̂k−1为已知量，所以Uk−1与Yk为非随机的确定序列，其对状态预测协方差矩阵和观测噪声不产生影响，则将式（10）代入（11）可得下一历元状态一步预测值为

相应地，状态方程一步预测值的协方差矩阵传递表达式为

根据卡尔曼滤波的量测更新阶段，k时刻经过量测修正的状态最优估计值为

式中Kk为卡尔曼增益，表示时间更新与量测修正的权重，其表达为

相应地，量测更新阶段的协方差矩阵为

综上所述，扩展卡尔曼滤波（EKF）算法的递推方程为

3 模型求解

3.1 状态更新

任意非领航无人机3个天线在导航坐标系中的状态方程为

式中Φk|k−1表示状态转移矩阵，非领航无人机的飞行状态参数为

式中I表示单位阵；τ=tk−tk−1表示观测周期间隔。

3.2 观测更新

3.2.1 1MA-1FA方案1MA-1FA编号表示一架主飞行器观测一架从飞行器的模型。式（8）给出了单架领航无人机对任意非领航无人机的观测方程，其相应的观测矩阵为

式中矩阵H内的各个块矩阵为

式中下标i表示主飞行器第i个天线，下标j表示从飞行器第j个天线。

3.2.2 3MA-1FA 方案3MA-1FA 编号表示3 架主飞行器观测一架从飞行器的模型。由式（8）给出的单架主机观测方程，可进一步得到3架主飞行器对单架从飞行器的观测方程为

相应地，其观测矩阵为

式中Hk表示第k（k= 1，2，3）架主飞行器对从飞行器的观测矩阵，且

式中Hk内部的块矩阵如式（13）所示。

3.3 导航参数更新

通过上述方法可估计出飞行器3 个天线的位置与速度信息，再根据天线在机身上固有的安装位置关系，可得到从飞行器机体坐标系的位置与速度信息为

根据式（3）和式（6），可进一步获得该飞行器在导航坐标系中的相对姿态角及其速率估值，即

式中滚动角γ表达式中的cij表示式（2）中旋转矩阵C内的元素，方位角速率ψ̇表达式中的cij表示式（7）中Jacobian 矩阵C2内的元素，此处i、j分别表示矩阵的行列；为避免ϑ解的双重性，一般取0°≤ϑ<180°；且当y>0时，ϑ符号取“+”；当y=0时，ϑ取“0°”；当y<0时，ϑ符号取“−”。

通过本节介绍的方法，即可估计出飞行器位置、速度、姿态角以及姿态角速率等相对导航参数。

4 仿真验证

4.1 基本数据

采用数值仿真方法对上述模型进行仿真实验研究。为便于分析本文建立的机间相对观测模型的可行性，假设领航无人机已经处于稳定飞行状态，非领航无人机相对于领航无人机的位置、姿态变化关系满足

式中f= 1/200表示飞行器姿态的周期变化频率。

已知每架无人机天线参数为a=1.0 m，b=1.0 m，主飞行器3 个天线发射的电磁波波长分别为λ1=1 m、λ2=2 m、λ3=3 m，频率取20 Hz。本文定义的导航坐标系中，1MA-1FA 方案对应的主飞行器点位为（0，0，0）m；3MA-1FA方案则按主飞行器疏密分布方式布置成两种情况：

1）取L=10 m，则主飞行器点位依次为（0，0，0）、（0，0，10）和（10，0，5）m；

2）取L=100 m，则主飞行器点位依次取（0，0，0）、（0，0，100）和（100，0，50）m。

4.2 初始条件

取初始时刻非领航无人机的位置状态误差为（-1.335 00，-1.621 60，-1.682 19）m，其速度状态误差为（0.818 60，0.686 10，0.741 50）m/s。相应地，位置初始协方差阵为diag（1.873 06，3.147 71，3.703 52），速度初始协方差阵为diag（0.699 28，0.460 08，0.505 87）。结合初始时刻飞行器姿态角与天线安装参数，则可得3个天线组成的初始时刻状态向量与协方差阵。考虑相位量测值服从高斯分布，其误差转换至距离观测量噪声为0.15（3σ）m，转换至速度观测量噪声取0.3（3σ）m/s。利用上述初始条件进行扩展卡尔曼滤波估计，其结果如4.3节所示。

4.3 结果与分析

根据上述方法，可得到1MA-1FA 方案和3MA-1FA（L=10 m，L10）方案的位置、速度滤波结果如图3和图4所示，姿态角及姿态角速度如图5和图6所示。

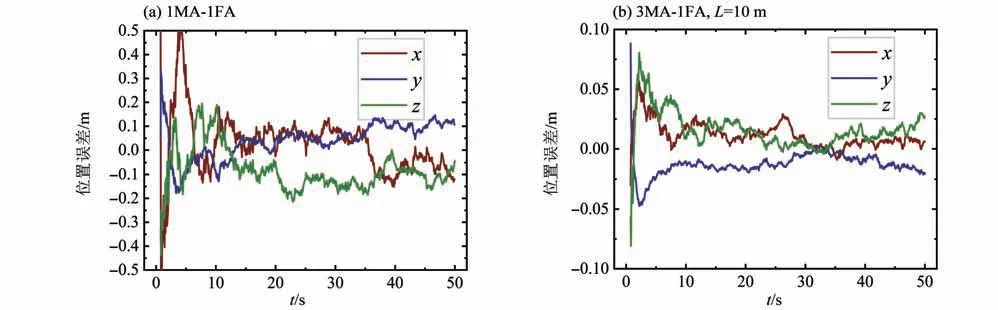
图3 位置误差曲线Fig.3 Position error curves

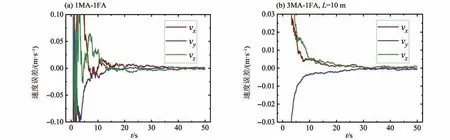
图4 速度误差曲线Fig.4 Velocity error curves

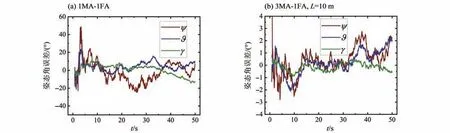
图5 姿态角误差曲线Fig.5 Attitude angle error curves

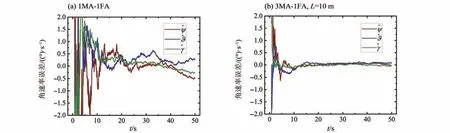
图6 姿态角速率误差曲线Fig.6 Attitude angular rate error curves

图3给出了位置估计误差变化曲线，由图可看出，1MA-1FA方案的结果震荡较为显著，误差在±0.2 m范围内波动，而3MA-1FA 方案的结果波动明显减小，误差小于0.1 m，且波动范围在±0.05 m 内，效果提升了75%，表明相比于单架主机，利用3架主机可显著提高对从飞行器的定位精度。图4给出了速度估计误差变化曲线。从图4可看出，两种方案滤波前期均存在较大误差，随着滤波时间推移，速度估计误差逐渐趋于收敛，相比于1MA-1FA 方案，3MA-1FA 方案具有更高的速度估计精度，而且3 个方向上的估计误差收敛至相同精度等级的速度更快。

图5与图6分别显示了姿态角误差和姿态角速率误差变化曲线。由图5可见，方案1MA-1FA中姿态角具有较大的误差，该结果与图3中位置误差相对应，此姿态角根据飞行器自身3个天线构成的几何关系进行求解，因此位置状态估计精度很大程度上决定了姿态角解算精度，从而导致1MA-1FA 方案中求解姿态角存在较大误差。但3MA-1FA 方案中姿态角误差显著减小，表明增加主飞行器数量，可明显提高从飞行器位姿估计精度。由图6 也可看出，3MA-1FA 方案较1MA-1FA 方案可得到更高的姿态角速率估计精度，且收敛速度更快。该姿态角速率根据飞行器自身天线存在的三角几何构型，利用位置速度状态估计值进行解算，因此与位置速度状态估计精度相关联，结合3MA-1FA 方案在位置和速度估计上具有较高的精度，从而求解出的姿态角速率能收敛到较好的精度范围。

3MA-1FA方案中，针对3架主飞行器布置较为分散（L=100 m，L100）的情况，其位置、速度滤波结果如图7所示，姿态角及其速率解算估值如图8所示。

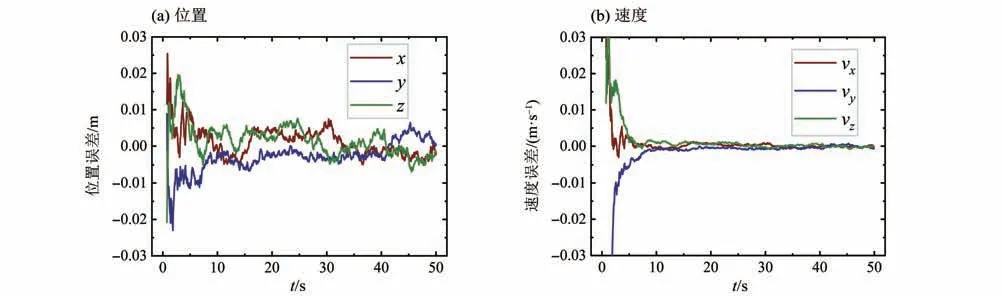
图7 位置和速度误差曲线（3MA-1FA，L=100 m）Fig.7 Position and velocity error curves

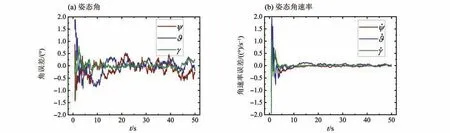
图8 姿态角和姿态角速率误差曲线（3MA-1FA，L=100 m）Fig.8 Attitude angle and attitude angular rate error curves

图7（a）显示了位置误差变化曲线。从图7（a）可看出，L100 布置方式可获得更高的滤波估计精度，位置误差在±0.01 m 范围内波动，其估计精度较图3 中L10 方式提高了80%。图7（b）显示了速度误差变化曲线，可明显看出L100 布置方式的速度收敛得更快，较图4 中L10 方式提升了约33.3%。图8（a）和图8（b）分别给出了姿态角及其速率估值误差曲线，从中可看出，L100 布置方式的姿态角误差显著减小，速率估值与L10 相当，且姿态角波动范围较图5 中L10 更稳定，相比于1MA-1FA 方案，效果提升愈加明显。从L10 与L100 的结果对比中，表明了相比于密集分布，分散布置可显著提高无人机集群的导航定位性能。