单弯双扶涡轮钻具造斜能力预测方法研究

侯学军 钟文建 王居贺 杨斌 张明 孙辉 郭晓乐

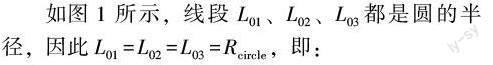
摘要：针对以钻头中心点、双扶正器中心点的三点定圆法预测的单弯双扶涡轮钻具曲率而不是井眼的曲率，造斜率预测误差较大等问题，改用钻头中心点、双扶正器中心点所对应的井眼轴线上3点，利用上下扶正器位置及井壁间隙、结构角大小和位置、偏心块的位置和偏心距等影响因素建立三点坐标；根据三点定圆数学原理，建立井眼轴线三点定圆全坐标单弯双扶涡轮钻具造斜率计算模型；以3种涡轮钻具为例，计算分析结构角位置与大小、上下扶正器的位置及其与井壁之间的间隙、井眼直径、偏心块位置与偏心距的大小等因素对单弯双扶涡轮钻具造斜能力，从定性到定量影响的变化规律。由此建议将偏心块安装在靠近钻头或结构角处，增大造斜率，并对比分析确定了涡轮钻具s理论和模型预测的实际的转换系数在1.28～1.37的合理范围内，验证了模型的可行性。研究结果可为高温深井涡轮定向钻井提供参考。

关键词：涡轮钻具；单弯双扶；定向钻井；三点定圆法；造斜能力；钻具组合

0 引 言

随着超深高温定向井日益增多，螺杆钻具因橡胶定子耐高温性能较差，将逐渐被金属结构耐高温涡轮钻具取代。涡轮和螺杆定向原理一样，有弯外壳、弯接头、偏心垫块3种。影响涡轮造斜率的因素有很多［1-2］，造斜率预测方法也较多，主要有平衡曲率法［3-5］、双半径法［6-8］、有限元法［9］、纵横弯曲法［10-11］、极限曲率法［12］、拟动态模拟法［13］和三点定圆法［14-15］等。

M.BIRADES等［3］根据将井眼曲率等于钻头侧向力为0时的平衡状态下钻具组合（BHA）的曲率提出平衡曲率法；狄勤丰等［4］根据地层抗钻特性提出了平衡侧向力法；张辉等［5］根据平衡法原理建立了地层力作用下的造斜率计算模型；B.R.HASSEN等［6］提出了双半径法；王宝新等［7］采用双半径法分析了双弯双扶和无扶动力钻具造斜率，计算了BHA曲率；孙建等［8］采用非线性有限元法，建立了中短半径水平井螺杆钻具力学模型；于永南等［9］用有限元方法分析了带弯接头BHA下部钻头侧向力的影响，确定了弯接头的位置；苏义脑等［10-12］将纵横弯曲法的小变形理论［13］拓展成钻具的大变形理论，实现求解钻头侧向力和倾角、稳定器支反力和内弯矩、钻具截面挠度和应力等功能，预测钻具造斜能力，并从底部BHA受力后发生弹性变形的力学角度提出极限曲率法［14］；郭宗禄等［15］采用拟动态模拟法对第一、第二扶正器直径大小、钻具弯角、井斜角、钻压等对BHA造斜稳斜的影响做了分析。但上述造斜率预测方法考虑因素多，模型大多比较复杂，不方便现场应用。

H.KARISSON等［14-15］運用三点定圆数学理论，将上下扶正器及弯角的中心点作为定圆三点，提出三点定圆法，预测动力钻具造斜率。但该方法忽略了上下扶正器位置的影响，误差大。后续学者以上、下扶正器和钻头的中心点为共圆三点不断改进三点定圆法：帅建等［16］考虑了下扶正器位置的影响；刘修善等［17-19］增加了结构弯角位置、下扶正器与井壁的间隙对造斜率的影响；吴振江等［20］增加了单弯螺杆钻具上扶正器外径、近钻头稳定器位置、井眼尺寸、钻压等对造斜率的影响；闫铁等［21］求解了双弯双扶BHA造斜率、增加了下扶正器与井壁间隙的影响值；王建斌等［22］分析了双弯双扶钻具下稳定器间隙和位置、以及弯角等对造斜率的影响。上述三点定圆法模型简单，方便应用，但所用共圆的三点都是在BHA轴线上的三点，受扶正器与井壁的间隙、钻具弯角等因素影响，BHA轴线和井眼轴线可能不重合；通过上、下扶正器中心和钻头中心的三点，定圆计算的曲率是BHA的曲率，不是井眼的曲率，因此存在原理性误差。

笔者针对上述三点定圆法的不足，考虑到近钻头扶正器偏心距和位置、扶正器与井眼之间的间隙和位置、弯角的大小和位置、BHA直径、井眼直径、钻柱长度等影响因素，将上、下扶正器中心点投影到井眼轴线上，再利用井眼轴线上的3点（钻头中心点、上下扶正器中心点在井眼轴线上的投影点）定圆原理，计算井眼轴线的曲率，以此提高对钻具造斜率的预测精度。

侯学军，等：单弯双扶涡轮钻具造斜能力预测方法研究

1 造斜率计算模型

1.1 三点定圆法造斜率计算模型

在实际钻井中，上下扶正器与井壁都有间隙，上下扶正器中心并不一定在井眼轴线所在的圆弧中心上。将坐标轴建立在近钻头钻具中心轴线上，上下扶正器中心所对应的井眼轴线上的点坐标点并不为零。因此将三点定圆坐标系由图1a改为图1b所示，点1、2、3分别为同一圆上的任意3点，以点1为原点，点2并不一定在坐标轴上，建立直角坐标系，根据三点定圆法推导井眼曲率计算模型。

2 造斜率计算参数

对于某区块井深≥7 600 m的井，采用涡轮定向钻进，钻井BHA为：149.2 mm孕镶金刚石钻头×0.368 m+120.6 mm涡轮钻具+120.6 mm无磁钻铤1根×1.88 m+MWD短接×4.85 m+120.6 mm钻铤+88.9 mm加重钻杆+88.9 mm钻杆+127.0 mm非标钻杆。

在后续的涡轮钻具的模拟分析中，假设δ1=δ2=1 mm，δ3=0，上扶正器紧贴井壁下侧，井眼直径为149.2 mm。3种涡轮钻具的结构和基本参数分别如图3和表1所示。

3 造斜率模拟分析

3.1 不同结构涡轮钻具造斜率对比分析

假设表1中涡轮钻具基本参数和井眼直径不变，计算上扶正器紧贴井壁上侧或下侧2种情况下造斜率随结构角变化情况（见图4）。结果表明：

（1）对于同一种结构的涡轮钻具，造斜率随结构角增大而线性增大；上扶正器紧贴井壁下侧时的每30 m造斜率比紧贴井壁上侧时的造斜率大0.4°～0.6°。

（2）对于不同结构的涡轮钻具，在结构角相等时，当涡轮钻具长度An＞As＞Ab（见表1）时，涡轮钻具造斜率Kn＜Ks＜Kb（见图4）。因此，在结构角相同时，涡轮钻具越短造斜率越大。

综上所述，在使用单弯涡轮钻具定向钻井时，可适当增加钻压，使上扶正器紧贴井壁下侧，提高造斜效果；对于不同结构的单弯涡轮钻具，在结构角相同时，应选择较短的涡轮钻具，提高造斜效果。

3.2 造斜率K与扶正器位置关系

3.2.1 涡轮钻具造斜率K与下扶正器位置D关系

仅改变单弯双扶正器涡轮钻具中下扶正器的位置，其他参数如表1不变，计算单弯双扶正器涡轮钻具造斜率K随下扶正器到钻头距离D的变化曲线，如图5所示。结果表明：

（1）同一涡轮钻具，结构角越大造斜率越大。

（2）同一涡轮钻具，涡轮钻具造斜率随下扶正器离钻头的距离D增大而增大，即：下扶正器距离钻头越近，距离结构角位置越远，造斜率越小。因此要使涡轮钻具造斜率增大，应让下扶正器远离钻头，安装在靠近结构角的位置。

（3）涡轮钻具结构不同，造斜率随下扶正器离钻头距离D的增大而变化程度不同：涡轮钻具b的结构角离钻头距离最短（见表1），造斜率Kb随下扶正器到钻头的距离增加而增加的幅度最大（见图5）；涡轮钻具n和涡轮钻具s的结构角离钻头距离较短，且Cn=1.600 m与Cs=1.676 m差别不大（见表1），造斜率Kn和Ks随下扶正器到钻头的距离增大而增加的幅度差别不大，但都比Kb增幅小（见图5）。

综上所述，要增加单弯涡轮钻具的造斜率，可以选择结构角较大和结构角离钻头距离最短的单弯涡轮钻具；同时，使下扶正器远离钻头，靠近结构角位置，以增强造斜效果。

3.2.2 涡轮钻具造斜率K与上扶正器位置B的关系

仅改变单弯双扶涡轮钻具上扶正器的位置B，其他参数如表1不变，计算单弯双扶涡轮造斜率K随上扶正器到钻头距离B变化的曲线，如图6所示。结果表明：

（1）随着上扶正器到钻头的距离B的增大，涡轮钻具n和s造斜率先增大后减小。

（2）涡轮钻具结构角位置C不同，最大造斜率所对应的上扶正器位置B不同：涡轮钻具n和s的结构角到钻头的距离C相近（Cn=1.600 m和Cs=1.676 m），因此都在B≈4 m处造斜率增加到最大，然后再随B的增大呈线性减小。涡轮钻具b的结构角到钻头的距离B最小（0.980 m），在γb≥1.5°时，B≈2.3 m处造斜率达到最大，然后再随B增加呈线性减小；在γb＜1.5°时，B≈3 m处造斜率达到最大，然后再随B的增大呈线性减小。

综上所述，要提高造斜效果，对于单弯涡轮钻具n和s，应将上扶正器安装在距离钻头B≈4 m处。对于单弯涡轮钻具b，当γb≥1.5°时，应将上扶正器安装在距离钻头B≈2.3 m；在γb＜1.5°时，应将上扶正器安装在距离钻头B≈3 m处。

3.3 涡轮钻具造斜率与扶正器井眼间隙关系

3.3.1 涡轮钻具造斜率K与下扶正器井眼间隙δ1关系

仅改变单弯双扶涡轮钻具下扶正器与井眼间隙δ1，其他参数如表1不变，计算单弯双扶涡轮造斜率K随下扶正器井眼间隙δ1变化曲线，如图7所示。结果表明：

（1）当涡轮钻具结构角γ≥1°时，涡轮钻具n、b、s的造斜率随下扶正器井眼间隙δ1的增大而呈线性下降。因此，用涡轮钻具定向造斜时，在不卡钻的前提下，应尽可能减小下扶正器与井壁的间隙δ1，同时增加涡轮钻具的结构角γ，以提高造斜效果。

（2）当涡轮钻具结构角γ≤0.5°时，涡轮钻具n、b、s的造斜率K随下扶正器井眼间隙δ1增大先线性下降到K≈0时，再随下扶正器井眼间隙δ1增大而增大。因此，在涡轮钻具结构角γ≤0.5°时，下扶正器与井壁间隙δ1达到一定程度（≥2.0 mm）时，有可能使涡轮钻具增斜失灵。

综上，对松软地层，下扶正器与井眼之间间隙δ1容易增大，不宜选用结构角γ≤0.5°的涡轮钻具，应尽可能选用结构角γ≥1°的涡轮钻具，以提高增斜效果。

3.3.2 涡轮钻具造斜率K与上扶正器井眼间隙δ2的关系

仅改变单弯双扶涡轮钻具上扶正器井眼间隙δ2大小，其他参数如表1不变，计算单弯双扶涡轮造斜率K随上扶正器井眼间隙δ2变化曲线，如图8所示。结果表明，涡轮钻具造斜率K随上扶正器井眼间隙δ2增大而减小，但减小的幅度非常小，表明上扶正器与井壁之间的间隙δ2对涡轮钻具造斜率K影响较小。

故在实际造斜应用中，为减小井下扶正器卡钻的风险，可适当减小上扶正器外径，增大上扶正器井眼间隙δ2，或者不使用上扶正器。

3.4 涡轮钻具造斜率K与下扶正器偏心距δ3的关系

3.4.1 涡轮钻具造斜率K与下扶正器偏心距δ3的关系

仅改变单弯双扶涡轮钻具下扶正器偏心距δ3大小，其他参数如表1所示，计算单弯双扶涡轮造斜率K随下扶正器偏心距δ3變化曲线如图9所示。结果表明：

（1）同一涡轮钻具造斜率K随下扶正器偏心距δ3增大而线性增大，且增大的幅度比较明显。

（2）当结构角γ相等时，涡轮钻具n、b、s的结构角到钻头的距离Cn=1.600 m与Cs=1.676 m相近，大于Cb=0.98 m，涡轮钻具造斜率K随下扶正器偏心距δ3增大而线性增大的幅度ΔKn≈ΔKs<ΔKb。

综上所述，要增大单弯涡轮钻具的造斜效果，在确保不卡钻的前提下，可采用偏心距较大的偏心扶正器，同时使用单弯涡轮钻具b优于使用单弯涡轮钻具n和s。

3.4.2 涡轮钻具造斜率K与偏心下扶正器位置D的关系

设下扶正器偏心距δ3=9 mm，改变单弯双扶正器涡轮钻具偏心下扶正器位置D，其他参数如表1不变，计算单弯双扶涡轮造斜率K随偏心下扶正器位置D变化曲线，如图10所示。结果表明：

（1）结构角γ≥1°时，随着下偏心扶正器到钻头的距离D增大，3种涡轮钻具的造斜率K先减小后增大，且钻具弯角越大，造斜率K先减小后增大的幅度均越大；结构角位置距离钻头的距离越长，造斜率K先减小后增大的幅度越大，且增大幅度ΔKn≈ΔKs＞ΔKb。

（2）结构角γ≤0.5°时，涡轮钻具n和s的造斜率随着下偏心扶正器到钻头的距离D增大先减小后微小增加；涡轮钻具b的造斜率随着下偏心扶正器到钻头的距离D增大而减小。

（3）同一涡轮钻具n、b、s，当结构角γ≥2.5°时，偏心下扶正器靠近结构角时的造斜率大于偏心情况下扶正器靠近钻头时的造斜率；当结构角γ≤2°时，偏心下扶正器靠近结构角时的造斜率小于偏心情况下扶正器靠近钻头时的造斜率。

综上所述，要增大偏心下扶正器造斜效果，当γ≥2.5°时，偏心情况下扶正器应安装在靠近结构角的位置；当γ≤2°时，偏心情况下扶正器应安装在靠近钻头的位置。

4 涡轮钻具造斜率试验数据对比分析

涡轮钻具s的理论造斜率是在假设钻头侧向力为0时，从几何角度建立的涡轮钻具造斜率计算模型计算出来的造斜率。计算模型计算了实际应用中由钻头侧向力、钻具弹性变形、地层造斜特性等多种因素造成的井径扩大或缩小的井眼间隙、偏心扶正器偏心距、上下扶正器的位置等影响，用该模型计算涡轮钻具定向钻井形成井眼的曲率，比涡轮钻具自身的造斜率小，且更准确。

根据s涡轮钻具厂家提供的涡轮钻具造斜率Ks（理论）数据，对比该模型计算实际井眼曲率K′s（见表2），结果表明：

（1）同一涡轮钻具，相同结构角时，Ks＞K′s，验证了模型计算实际井眼曲率K′s小于涡轮钻具的理论造斜率Ks的推断，说明该模型用于计算井下涡轮钻具造斜率可行。

（2）同一涡轮钻具，相同结构角时，涡轮钻具理论造斜率Ks是该模型计算的实际造斜率Ks′的1.28～1.37倍。根据极限曲率法［14］，Ks/Ks′取值1.18～1.43，且1.18＜1.28≤Ks/K′s≤1.37＜1.43，说明该模型计算的实际井眼曲率范围比极限曲率法计算曲率范围更精确，验证了该模型用于计算井下涡轮钻具造斜率切实可行。

5 结论及认识

（1）将三点定圆从钻具轴线上的上下扶正器中心点和钻头中心点变成上下扶正器中心点和钻头中心点在井眼轴线上的垂直投影点，提出三点定圆全坐标单弯双扶涡轮钻具造斜率预测模型，全面综合考虑了单弯双扶涡轮钻具结构角大小和位置、扶正器间隙和位置、下偏心扶正器偏心距等对造斜率的影响，将三点定圆法从计算钻具轴线曲率转移到计算井眼轴线曲率。

（2）模拟计算了3种结构的涡轮钻具造斜率，分析了涡轮钻具造斜率随结构角大小和位置、上下扶正器与井壁的间隙和位置、下偏心扶正器的位置和偏心距从定性到定量的变化规律，建议将偏心块安装在靠近钻头或结构角处，增大造斜率，为单弯双扶涡轮钻具定向钻井提供指导。

（3）通过对比涡轮钻具造斜率的理论数据和实践数据，证明全坐标三点定圆单弯双扶涡轮钻具造斜率计算模型更准确、可行。

参考文献：

［1］ 高德利．影响井眼轨迹的诸种因素［J］．石油钻采工艺，1992（2）：27-34，40．

GAO D L.The factors that affect the well trajectory［J］.Oil Drilling & Production Technology，1992（2）：27-34，40.

［2］ 苏义脑．导向钻具选型与总体设计的原则和方法［J］．石油钻采工艺，1999，21（3）：18-27．

SU Y N.The principle and method for selection and master design of guide drill tool［J］.Oil Drilling & Production Technology，1999，21（3）：18-27.

［3］ BIRADES M，FENOUL R.A microcomputer program for prediction of bottom hole assembly trajectory［J］.SPE Drilling Engineering，1988，3（2）：167-172.

［4］ 狄勤豐，彭国荣．下部钻具组合造斜能力的预测方法研究［J］．石油钻采工艺，2000，22（2）：17-19．

DI Q F，PENG G R.A new method for predicting the deflecting capacity of bottom hole assembly［J］.Oil Drilling & Production Technology，2000，22（2）：17-19.

［5］ 张辉，张日鹏，何军，等．单弯螺杆钻具组合造斜能力研究［J］．长江大学学报（自科版），2016，13（2）：41-46．

ZHANG H，ZHANG R P，HE J，et al.Study on build-up capacity of positive displacement drill （PDD）wit single bend［J］.Journal of Yangtze University （Natural Science Edition），2016，13（2）：41-46.

［6］ HASSEN B R，MACDONALD A J.Field comparison of medium and long-radius horizontal wells drilled in the same reservoir［C］∥IADC/SPE Drilling Conference.Houston，Texas：IADC/SPE，1990：SPE 19986-MS.

［7］ 王宝新，许岱文，程存志．弯壳动力钻具造斜率的几何分析与计算［J］．石油钻采工艺，1994，16（1）：32-37．

WANG B X，XU D W，CHENG C Z.Geometric analysis and calculation of build-up rate of motor drilling tool［J］.Oil Drilling & Production Technology，1994，16（1）：32-37.

［8］ 孫健，李黔，王治平，等．中短半径水平井造斜率与螺杆钻具应力研究［J］．天然气工业，2007，27（6）：78-80．

SUN J，LI Q，WANG Z P，et al.Built-up rate and PDM's stress analysis for medium-and short-radius horizontal wells［J］.Natural Gas Industry，2007，27（6）：78-80.

［9］ 于永南，帅健，吕英民．带弯接头下部钻具组合的特性分析［J］．石油钻采工艺，1993，15（4）：8-13．

YU Y N，SHUAI J，LYU Y M.Characteristic analysis of BHA with bent joint［J］.Oil Drilling & Production Technology，1993，15（4）：8-13.

［10］ 苏义脑．求解井底钻具组合大变形的纵横弯曲法及其在导向钻具组合分析中的应用［J］．石油钻采工艺，1994，16（6）：1-6．

SU Y N.Solution of BHA under large deformation by beam-column theory and its use in stearable bha analysis［J］.Oil Drilling & Production Technology，1994，16（6）：1-6.

［11］ 白家祉，林小敏．纵横弯曲法对钻具组合的二维分析［J］．石油学报，1985，6（3）：75-84．

BAI J Z，LIN X M.Two-dimensional analysis of bottom hole assembly by beam-column theory［J］.Acta Petrolei Sinica，1985，6（3）：75-84.

［12］ 苏义脑．极限曲率法及其应用［J］．石油学报，1997，18（3）：110-114．

SU Y N.A method of limiting curvature and its applications［J］.Acta Petrolei Sinica，1997，18（3）：110-114.

［13］ 郭宗禄，高德利，张辉．单弯双稳导向钻具组合复合钻进稳斜能力分析与优化［J］．石油钻探技术，2013，41（6）：19-24．

GUO Z L，GAO D L，ZHANG H.Analysis and optimization of holding-inclination capability of steerable assembly with single bend and two stabilizers［J］.Petroleum Drilling Techniques，2013，41（6）：19-24.

［14］ KARISSON H，BRASSFIELD T，KRUEGER V，et al.Performance drilling optimization［C］∥SPE/IADC Drilling Conference.New Orleans，Louisiana：SPE/IADC，1985：SPE 13474-MS.

［15］ KARLSSON H，COBBLEY R，JAQUES G E.New developments in short-，medium-，and long-radius lateral drilling［C］∥SPE/IADC Drilling Conference.New Orleans，Louisiana：SPE/IADC，1989：SPE 18706-MS.

［16］ 帅健，于永南，洪学福．短弯外壳导向钻具的造斜率计算［J］．石油钻采工艺，1996，18（1）：4-9．

SHUAI J，YU Y N，HONG X F.Build-up rate calculating on short bent housing motor［J］.Oil Drilling & Production Technology，1996，18（1）：4-9.

［17］ 刘修善，何树山，邹野．导向钻具几何造斜率的研究［J］．石油学报，2004，25（6）：83-87．

LIU X S，HE S S，ZOU Y.Study on the geometric build angle rate of steerable motor［J］.Acta Petrolei Sinica，2004，25（6）：83-87.

［18］ 刘修善．导向钻具几何造斜率的实用计算方法［J］．天然气工业，2005，25（11）：50-52．

LIU X S.Practical calculation method of geometric deflection rate of guide drilling tool［J］.Natural Gas Industry，2005，25（11）：50-52.

［19］ 刘修善，王成萍，程安林．弯壳体导向钻具的设计方法［J］．石油钻采工艺，2005，27（4）：18-20，23．

LIU X S，WANG C P，CHENG A L.Design method of bend housing steerable drill tool［J］.Oil Drilling & Production Technology，2005，27（4）：18-20，23.

［20］ 吴振江，柳贡慧，李军．螺杆钻具造斜能力分析及预测［J］．石油矿场机械，2009，38（8）：61-65．

WU Z J，LIU G H，LI J.Analysis and prediction of build-up rate using screw drill［J］.Oil Field Equipment，2009，38（8）：61-65.

［21］ 闫铁，王辉，毕雪亮．弯壳体导向钻具造斜能力影响因素分析［J］．西部探矿工程，2010，22（1）：35-39．

YAN T，WANG H，BI X L.BI xueliang.The influential factors analyses of bent housing steerable-motor's build angle capability［J］.West-China Exploration Engineering，2010，22（1）：35-39.

［22］ 王建斌，熊青山，鲁洪清，等．双弯螺杆钻具几何造斜率计算式的修正［J］．石油机械，2016，44（12）：25-28，73．

WANG J B，XIONG Q S，LU H Q，et al.Correction of geometrical build-up rate formula of double tilt PDM［J］.China Petroleum Machinery，2016，44（12）：25-28，73.