基于PCA-LSTM的黏滑振动水平评估方法研究

张鑫 张涛 李玉梅 房萍

摘要：石油钻井过程中，井下工具的黏滑振动会导致钻头发生周期性的黏滞和滑脱，容易引起钻头和钻具组合失效，造成井下事故。为此，基于井下测量技术的发展，采用长短期记忆（Long Short-term Memory，LSTM）神经网络智能算法建立黏滑振动水平评估模型，采用井下近钻头工程参数测量工具在钻头处采集7类高频井下工程参数，验证使用PCA-LSTM神经网络黏滑振动水平评估模型的准确性。研究结果表明，该评估模型均方根误差为0.026，较LSTM、PCA-BP、PCA-SVM评估模型分别下降了0.033、0.011和0.018，表明该模型抑制了过拟合造成的滞后效应，具有较高的精度，可有效评估钻头处黏滑振动水平。研究结果对指导钻井过程，及时调整地面参数，有效抑制黏滑振动，推动安全、快速、高效钻井具有重要作用。

关键词：井下工具黏滑振动；随机森林；LSTM神经网络；近钻头；训练模型

0 引 言

在石油钻井中，井下振动主要包括3种形式：横向、轴向和扭转振动。不同的振动模式会导致不同的井下异常工况，例如：横向振动会导致钻头涡动，轴向振动会导致钻头跳钻，扭转振动会导致黏滑。发生黏滑振动时，钻头每隔几秒就会发生周期性的黏滞及滑脱，而地面顶驱却保持在恒定转速，钻头最大转速甚至可以超过2倍的地面顶驱转速，因此黏滑振动通常是钻头和钻具组合失效的重要原因［1-3］。近年来，为了提高钻井效率，降低井下事故风险，国内外针对井下异常振动的研究越来越多［4-7］。

随着井下测量技术的发展，近钻头处的三轴振动、转速、钻压及扭矩等工程数据已可以测量。北京工业大学柳贡慧团队［8］研发了井下双测点多参数随钻测量工具，该工具可测量井下近钻头处环空压力、管内温度、钻压、扭矩、三轴振动等多个参数，同时可扩展测量环空流体的介电常数。滕学清等［9］对来自深井及超深井的井下振动数据进行了分析，对比振动数据在时域内的均值、峰值和均方根值，以及快速傅里叶变化后的频域数据，确立了深井钻柱黏滑振动的时域及频域特征。唐翰文等［10］通过分析近钻头振动数据特征，建立了基于XGBoost的黏滑振动等级分类模型。E.Z.LOSOYA等［11］利用历史数据建立机器学习模型，放置于井下钻头处，通过直接获取井下钻头处的高频工程参数，以实现实时识别井下异常振动造成的黏滑、涡动等复杂工况。T.BAUMGARTNER等［12］从高频振动数据中提取和分析基本特征，建立了基于贝叶斯算法的振动模式识别模型。

笔者采用长短期记忆（Long Short-term Memory，LSTM）神经网络智能算法建立黏滑振动水平评估模型。在此之前，陈冲等［13］提出一种基于因子分析和支持向量机的黏滑振动等级评估方法。ZHA Y.等［14］利用地面测量数据，通过深度神经网络建立了井下异常振动事件分类识别模型。LAN B.等［15］利用地面数据建立了基于LSTM神经网络的ROP钻速预测模型，以指导地面工作人员优化钻井。由于地面测量数据与井下钻头处的实际数据有较大差异，所以笔者依据北京信息科技大学智能钻井实验室自主研发的井下近钻头工程参数测量工具，对在钻头处采集到的7类高频井下工程参数开展研究，应用监督式学习分类对井下黏滑振动进行识别，以确定钻头在钻进时是否发生了黏滑振动，并使用LSTM神经网络评估它们的振动水平。

1 黏滑振动特性分析

以塔里木油田富满区块某三开井段所开展的试验为例分析。试验地层为石炭系、泥盆系，地层岩性为砂岩、泥岩、灰岩、大套细砂岩。钻进参数包括：转盘转速75～80 r/min，钻压50～80 kN，钻井液排量27 L/s，钻井液密度1.31 g/cm3。试验钻进深度为5 449～5 635 m，累计进尺186 m。

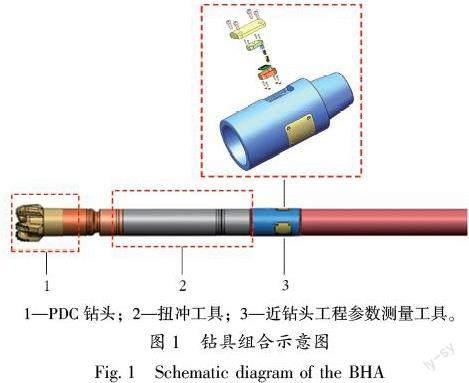
由于钻头与岩石相互作用，使用PDC钻头时，黏滑表现为一种由自激产生的低频扭转振动。图1为钻具组合示意图。在PDC钻头上方连接扭冲工具，扭冲工具的上方连接近钻头工程参数测量工具，连接扣型均为114.3 mm（41/2 in） REG螺纹。

在图2中标示出1个周期内钻头黏滑时近钻头工程参数的变化特征。时域分析结果表明：在位置①处转速接近于0，钻头开始黏滞，振动较弱，扭矩逐渐增加；在位置②处扭矩增加到能够克服摩擦力作功，转速开始增加，扭矩开始减小，钻头开始滑脱，振动逐渐增大；在位置③处转速达到峰值，扭矩最小，在横向振动的作用下，钻头轻微抬起，钻压减小；在位置④处转速再次减小直至钻头黏滞，振动再次减弱。钻头黏滑振动呈现出周期性变化。根据黏滑振动期间转速与时间变化曲线可大致确定，黏滑振动周期约为9 s，其中黏滞时长约为3 s，滑脱时长约为6 s。与此同时，三轴振动也呈现出相同的周期性规律。切向和法向振动均以0g（g为重力加速度）为中心上下剧烈波动，峰值在10g以上；而轴向振动不以0g为中心上下波动，峰值约为5g，反映了直井重力加速度的特征；振动较轻时，切向和法向振动接近0g，轴向约为1.5g，反映此时钻头处于微弱振动状态。

图3为钻头正常钻进时参数变化特征。由图3可以看出：钻头的钻压、扭矩、转速均在一定区间内波动，变化幅度较小；钻头的切向、法向及轴向振动峰值均低于7.5g，钻进平稳。黏滑振动不仅影响钻井效率，还容易造成井下钻具组合提前失效，时域特征虽然可以大致判断黏滑振动，但是由于影响因素较多，阈值范围广，难以实现计算机自动识别，所以需要进一步提取信号特征并建立智能识别模型。

2 算法原理

2.1 特征方程

井下發生黏滑振动时，时域特征量可以在一定程度上分辨出信号随时间的变化特征，而频域特征量可以反映信号在不同频率上的分布情况。本文对近钻头钻压、扭矩、转速、三轴振动等测量数据提取6类时域特征值。对三轴振动测量数据进行快速傅里叶变换（Fast Fourier Transform ，FFT），将时域数据转化为频域数据，以提取6类频域特征值。提取的时域特征值及频域特征值指标计算公式列于表1之中。表1中，x（j）为时域信号序列，s（k）是x（j）的频谱序列，其中k=1，2，…，k，fk为第k条谱线的频率值，n为时域信号长度，K为频谱线数量。

2.2 智能识别模型

2.2.1 随机森林模型

随机森林是一种决策树的集成算法，可以由多个ID3、C4.5等决策树组成。每棵树都是独立的，彼此无关［16］。随机森林可以应用于高维、大数据量的分类算法，具有速度快、精度高、不易过拟合的特点，即使数据的大部分特征丢失，也可以保持良好的准确性。森林中的每一棵树都可以用于分类，实际上可以形成多个分类器。本质上，随机森林通过在数据集中随机放回样本来构建子数据集，并建立多个决策树。对于同一个输入样本，多棵树会产生多个分类结果。随机森林对每个分类结果进行投票，选择得票最多的类别作为分类的最终输出。本研究所用的高频井下近钻头工程参数测量数据的数据量庞大，适宜采用随机森林建模。

2.2.2 LSTM神经网络模型

长短期记忆网络是一种循环神经网络（Rerrent Neural Network，RNN）的变体。该网络能够有效解决长程依赖问题［17］。相比于其他神经网络，循环神经网络（RNN）中的神经元除了接受其他神经元的信息外，还能接受自身的信息。

图4为RNN单元结构示意图。图4中，xt为当前时刻的输入值，ht为隐藏层的输出值，ht-1为隐藏层上一时刻的输出值，延迟器是一个虚拟单元，用来记上次（或上几次）隐藏层的输出值。RNN中通常使用Logistic或Tanh函数作为激活函数，这些函数导数值小于1，故经常出现梯度消失问题。而LSTM引入门控单元控制信息的传递，能够有效改善RNN单元结构中梯度消失和梯度爆炸问题。

3 基于LSTM神经网络智能算法的黏

滑振动评估方法

3.1 数据预处理

此次研究采用新疆富满油田某井井下高频近钻头工程参数，测量工具为北京信息科技大学自主研发的井下近钻头多参数测量短节等。该仪器测量参数及精度如表2所示。

钻头累计钻进23 h，设置工具采集频率为400 Hz。对原始数据提取特征向量，以减少模型处理数据量，节约模型训练时间。井下高频测量数据由于井下环境复杂及传感器本身误差，往往带有不同程度的噪声，因此需通过高斯平滑函数进行去噪。如图2所示，由于单个黏滑周期大约为9 s，所以为保证每段数据内至少包含1个黏滑周期，以每10 s数据为1组，全段共计得到7 200组数据，每组数据包含钻压、扭矩、转速、三轴振动数据。对各组数据进行时域分析得到36个时域特征，对三轴振动数据进行频域分析得到18个频域特征。

3.2 LSTM神经网络黏滑振动评估模型与方式

LSTM神经网络黏滑振动评估工作流程如图6所示。选取正常钻进数据200组、黏滑振动数据300组，共计500组测量数据，构建黏滑振动识别数据集，其中训练集占70%，测试集占30%。采用随机森林建立分类识别模型，随机森林模型可以较好地分类识别正常钻进和黏滑振动。模型单个工况识别精度分别为91.6%和97.8%，综合识别准确率达95.3%。混淆矩阵见表3。

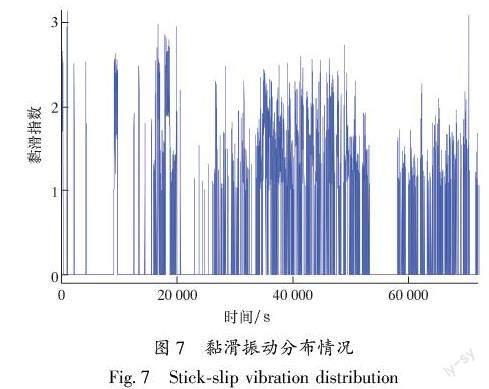
钻头转速可由井下近钻头工程参数测量工具测得，ISS值越大，证明井下振动越激烈，黏滑振动水平越高。应用建立好的随机森林模型对上述井段中7 200组数据进行分类识别。图7显示了经过随机森林分类识别后，在该井井下黏滑振动的分布情况，正常钻进时ISS值用0表示。由图7可知，黏滑振动在该井段的分布符合实际规律，因此ISS值可以作为LSTM神经网络黏滑振动水平评估的结果。

将7 200组数据分割为训练集和测试集，并对数据进行归一化处理，其中70%数据用于训练模型，其余30%用于测试训练模型的准确性。采用PCA-LSTM神经网络建立回归模型。利用PCA对钻压、扭矩、转速、三轴振动的时域特征及频域特征共54维特征值向量进行降维，选取贡献率排名前10的特征值作为输入层，使用6个隐藏层，每层96个神经元来构建LSTM神经网络。共计进行100轮训练，在60轮训练后，通过乘以因子0.2来降低学习率，防止过拟合。最后利用一个神经元输出层评估10 s后黏滑振动水平。

3.3 黏滑振动评估结果

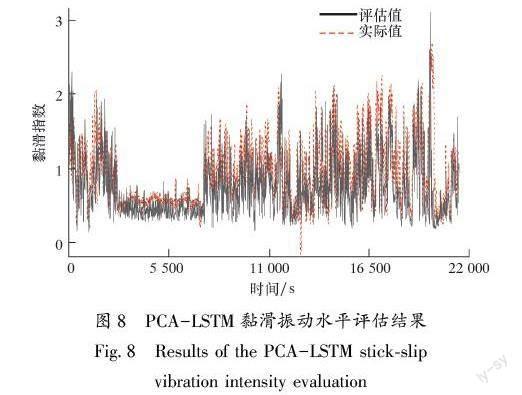
使用训练好的PCA-LSTM模型，对测试集进行测试，并利用均方根误差对测试结果进行评价，结果如图8所示。

经过训练的PCA-LSTM模型黏滑振动水平的评估结果能够很好地反映井下实际状态，与实际振动水平一致，没有明显的滞后效应。该PCA-LSTM模型具有较高的精度，均方根误差值仅为0.026，可以有效对井下黏滑振动水平进行评估，并运用到实际钻井中。根据评估结果调整地面参数，能够有效抑制黏滑振动，降低事故发生风险，对指导安全、快速、高效钻井具有重要意义。

为了验证PCA对LSTM黏滑振动水平评估模型滞后效应的抑制效果，对比了PCA-LSTM和LSTM评估模型的评估结果，对比结果如图9和表4所示。由于数据具有较高的相关性，LSTM评估模型将前一组的真实数据作为后一组的输出值，评估结果表现出强烈的滞后效应，出现了过度拟合。而PCA-LSTM模型有效地抑制了滞后效应，评估结果更贴近实际值，提升了模型的精度，均方根误差值较LSTM评估模型降低了0.033。

为了验证PCA-LSTM模型评估黏滑振动水平的优越性，本文进一步将PCA降维后的数据与支持向量机（Support Vector Machine ，SVM）和BP神經网络模型的评估结果对比，其对比结果如图10和表5所示。由图10和表5可知，使用PCA-LSTM评估模型的均方根误差相比于PCA-BP、PCA-SVM评估模型分别下降了0.011和0.018。因此，LSTM神经网络模型可以更好地挖掘样本间的时序相关性，比BP和SVM更适合用于评估井下黏滑振动水平。

4 结 论

（1）利用近钻头工程参数测量工具采集的井下工程数据，为分析黏滑振动水平提供了数据支撑。常规的时域特征阈值方法识别准确率低，难以实现计算机自动识别。而应用随机森林机器学习模型，对井下黏滑振动进行识别，整体准确率高达95.3%。

（2）通过对井下近钻头工程参数测量数据分析，得到黏滑振动指标ISS，可用来量化评估井下钻头处的黏滑振动水平。

（3）本文提出的PCA-LSTM井下黏滑振动评估模型，解决了LSTM评估模型的滞后效应，相较于LSTM、PCA-SVM和PCA-BP评估模型，其均方根误差分别降低了0.033、0.018和0.011，精度更高，可以更好地挖掘样本间时序相关性，更适合用于评估井下黏滑振动水平。

参考文献：

［1］ NORDIN M H，LOOI L K，SLAGEL P，et al.Minimising torsional vibration due to stick slip using Z technology for drilling energy efficiency in multiple hard stringers field in offshore Malaysia［C］∥International Petroleum Technology Conference.Virtual： IPTC，2021： IPTC 21841-MS.

［2］ LEDGERWOOD L W，HOFFMANN O J，JAIN J R，et al.Downhole vibration measurement，monitoring，and modeling reveal stick/slip as a primary cause of PDC-bit damage in today［C］∥SPE Annual Technical Conference and Exhibition.Florence，Italy： SPE，2010： SPE 134488-MS.

［3］ 牟海維，王瑛，韩春杰．钻柱的黏滑振动规律分析［J］．石油机械，2011，39（3）：67-69，81.

MU H W，WANG Y，HAN C J.Analysis of the stick-slip vibration pattern of the drill string［J］.China Petroleum Machinery，2011，39（3）： 67-69，81.

［4］ ZHAO F，WANG H G，CUI M.Optimizating drilling operating parameters with real-time surveillance and mitigation system of downhole vibration in deep wells［C］∥IADC/SPE Asia Pacific Drilling Technology Conference.Singapore： SPE，2016： SPE 180661-MS.

［5］ CHEN S L，WISINGER J，DUNBAR B，et al.Identification and mitigation of friction-and cutting-action-induced stick/slip vibrations with PDC bits［J］.SPE Drilling & Completion，2020，35（4）： 576-587.

［6］ 陈会娟．井下钻柱振动信号的测量及振动激励源研究［J］．石油钻探技术，2021，49（5）：57-63.

CHEN H J.Measurement of the downhole drill string vibration signal and analysis of the vibration excitation sources［J］.Petroleum Drilling Techniques，2021，49（5）： 57-63.

［7］ 查春青，柳贡慧，李军，等．PDC钻头扭转振动特性分析及减振工具设计［J］．石油机械，2017，45（3）：1-5.

ZHA C Q，LIU G H，LI J，et al.Analysis of torsional vibration characteristics of PDC bit and design of the damping tool［J］.China Petroleum Machinery，2017，45（3）： 1-5.

［8］ WANG C，LIU G H，LI J，et al.Non-uniform temperature distribution's impact on downhole weight on bit （DWOB） measurement and the novel compensatory method［J］.Journal of Petroleum Science and Engineering，2020，184：106528.

［9］ 滕学清，狄勤丰，李宁，等．超深井钻柱黏滑振动特征的测量与分析［J］．石油钻探技术，2017，45（2）：32-39.

TENG X Q，DI Q F，LI N，et al.Measurement and analysis of stick-slip characteristics of drill string in ultra-deep wells［J］.Petroleum Drilling Techniques，2017，45（2）： 32-39.

［10］ 唐翰文，张涛，李玉梅，等．基于优化XGBoost的近钻头黏滑振动等级评估方法［J］．系统仿真学报，2021，33（11）：2704-2710.

TANG H W，ZHANG T，LI Y M，et al.Research on stick-slip vibration level estimation of near-bit based on optimized XGBoost［J］.Journal of System Simulation，2021，33（11）： 2704-2710.

［11］ LOSOYA E Z，VISHNUMOLAKALA N，GILDIN E，et al.Machine learning based intelligent downhole drilling optimization system using an electromagnetic short hop bit dynamic measurements［C］∥SPE Annual Technical Conference and Exhibition.Virtual： SPE，2020： SPE 201572-MS.

［12］ BAUMGARTNER T，VAN OORT E.Pure and coupled drill string vibration pattern recognition in high frequency downhole data［C］∥SPE Annual Technical Conference and Exhibition.Amsterdam，The Netherlands： SPE，2014： SPE 170955-MS.

［13］ 陳冲，张仕民，彭鹤，等．基于支持向量机的钻柱黏滑振动等级评估方法［J］．石油机械，2019，47（1）：20-26.

CHEN C，ZHANG S M，PENG H，et al.Research on stick-slip vibration level estimation of drillstring based on SVM［J］.China Petroleum Machinery，2019，47（1）： 20-26.

［14］ ZHA Y，PHAM S.Monitoring downhole drilling vibrations using surface data through deep learning［M］∥SEG.SEG Technical Program Expanded Abstracts 2018. Tulsa： Society of Exploration Geophysicists，2018： 2101-2105.

［15］ LAON B，JIN Y，PANG H W.Prediction of POR based on artificial neural network with long and short memory （LSTM）［C］∥55th U.S.Rock Mechanics/Geomechanics Symposium.Virtual： ARMA，2021： ARMA 2021-1454.

［16］ PAUL A，MUKHERJEE D P，DAS P，et al.Improved random forest for classification［J］.IEEE Transactions on Image Processing，2018，27（8）： 4012-4024.

［17］ VAN HOUDT G，MOSQUERA C，NPOLES G.A review on the long short-term memory model［J］.Artificial Intelligence Review，2020，53（8）： 5929-5955.