基于LSTM循环神经网络的织机了机预测

徐开心 戴宁 汝欣 胡旭东

摘 要：不同织机由于生产情况和影响参数各异，实际的织布效率和了机时间也存在着很大的差别。针对利用预先设定好的计划生产静态参数对织机了机时间进行计算时，存在理论计算值与实际织机了机时间偏差过大的问题，提出了一种基于长短时记忆（Long short term memory，LSTM）循环神经网络的织机了机预测方法。从织机经纬向停车情况、人员工作效率、加工布匹品种3个方面出发，分析影响织机了机时间的各类因素，构建了具有时间序列特性的织机生产情况数据集。通过设置时间进度系数动态调整模型在织轴整个生命周期内的预测情况，并从损失程度和训练耗时两方面考虑对模型性能进行优化。最后，利用8组实验数据对模型的可靠性进行验证。结果表明：模型在了机预测截止时间的前30 h至前6 h，模型的预测结果值与实际值之间的平均误差范围为0.84 h至1.52 h，满足对实际生产时的所需指标要求。

关键词：织机了机；LSTM循环神经网络；时间序列；经纬向停车；织轴

中图分类号：TS111.8

文献标志码：A

文章编号：1009-265X（2023）03-0070-11

基金项目：浙江省博士后科研项目择优资助项目（ZJ2021038）；浙江理工大学科研启动基金项目（11150131722114）

作者简介：徐开心（1998—），男，浙江嘉兴人，硕士研究生，主要从事纺织智能制造及数据化管理方面的研究。

通信作者：戴宁，E-mail：990713260@qq.com

织机的生产主要是将纬纱与织轴上的经纱纵、横向交织加工成布匹的过程［1］。当织机上织轴的纱线用尽时，需要将织轴、经停片、综、钢筘和经纱等从织机上清理下来，这个过程称为织机的了机［2］。织机了机过早，会使织轴的纱线原料浪费；织机了机不及时，则会造成机台停滞过久和剩余经纱长度不足而无法对新轴进行结经等问题［3］。对织机了机时间的准确预知，及时安排人员进行穿经、结经、换轴工作［4］，使新的织轴及时投入生产，对提高织造生产效益有着重要的影响作用。

要准确预知织机的了机时间，把控好织造环节的整体生产进度，其中，涉及到对生产车间内基础数据的实时采集以及利用数据驱动的方式，分析和挖掘出车间内的生产趋势和因素特性两部分要求。郭广慧等［5］利用移动终端和基于Web Service的访问数据库中间件架构，实现了对织机运行数据的监测；罗东升［6］提出了一种采用接口植入的织机数据获取方式，从而解决了由于设备异构而导致的系统不兼容问题。以上研究虽然已经做到了对车间数据的实时、完整收集，但未从海量数据中进行影响因素的挖掘，对生产中的变化趋势和突发情况没有做出考虑。郑宝平等［7］通过对经编机成圈机构的运动规律进行分析，设计了电子凸轮规划曲线算法和模型预测控制算法，实现了对纱线动态张力的补偿控制；张晓侠等［8］提出影响织机效率的最关键因素是经、纬向停车，并且利用反向传播（Back propagation，BP）神经网络及其改进算法对织机效率进行了预测。这些研究虽然对实际的生产数据进行了统计和分析，但多是基于从工艺参数等静态数据上考虑，未考虑到织机的各类生产数据与时间进度之间具有的关联性。

鉴于以上分析，本文将织机对织轴加工时的整个生命周期作为一个长时间序列，研究织机生产时的各类生产数据、生产时间对织机了机时间的关系，基于LSTM循环神经网络构建织机了机时间预测模型。

1 指标要求

为更符合实际生产要求，对织机了机预测的实际需求指标进行分析和确认。织造的工艺流程分为整经、浆纱、穿综、织布、验布［9］，作为典型的全流程生产，各道环节之间不间断作业是织造高效率生产的重要保证。织机织布前后的生产环节所需时间如表1所示。

通过调研得到，多数纺织厂的织布原材料为筒纱，首先需要经过整经、浆纱、穿综三道工序才能加工得到用于織机生产的织轴，期间所需要消耗的整体加工时间在8 h到11 h，为了能够更加贴合实际车间生产要求，使织机的织布生产有更加充足的准备时间，以及考虑到机器故障等额外可能发生的意外情况，对织机的了机预测应控制在织机实际了机的前1天甚至更早的时间才有参考意义。

了机预测时间的误差范围则与织机织前准备环节的所需时间有极大关联。从表1中可以得到，织机的织前准备环节可以分为拉轴、推轴、上轴以及织机开车前的最后检查4个工作步骤。其中，织轴上轴是织前准备环节中消耗时间最长的，包括纱线结经、工艺参数录入和布面检查等。织前准备环节所需要消耗的整体时间在2 h到3 h，为了能够给织前准备环节预留出充足的操作时间以及当遇到织机故障等情况时，能够给调度人员更多的改机计划时间，织机的了机预测时间与实际了机时间的误差应满足在3 h内。

结合以上两点要求，本文所设计的了机时间预测模型需要满足的需求指标约束如式（1）所示。

式中：k为时间进度索引；d为织机实际了机的前一天时间进度点；Tk为k时间进度下预测的了机时间，h；Tsj为织机的实际了机时间，h；Td为织机实际了机的前一天时间，h。

2 影响因素分析

织机了机时间的预测实际上是对织机加工完目标织轴所需时间的计算。根据织机在织布前预先设定的织布总米数、织机的运行车速和所织布匹品种要求的纬密参数，可计算得到，织机完成所设定达到的织布米长需要的理论织布时间，即织机的理论了机时间。其计算如式（2）所示。

式中：Tll为织机织布的理论总时间，min；M为织轴卷绕的纱线总长度，m；W为布匹的纬密参数值（布匹1英寸长度上的纬纱根数）；S为织机织布时的运行车速（织机1分钟的打纬次数）。

式（2）的计算默认织机在加工织轴的整个周期内为一直保持理想的织布运行状态，这不符合实际的生产情况。在实际生产场景下，织机织布过程中会因为纱线断裂或机器故障等原因而出现停车。织机实际织布时间与理论织布时间二者有如式（3）的关系。

式中：Tjw为织机在加工织轴整个周期内所产生的经纬向停车时间，h；To为织机在加工织轴整个周期内所产生的其他情况停车时间，h。

因此，要做到准确预测织机了机时间的难点，在于如何准确把握织机织布过程中不定时出现的停车而额外对生产增加的消耗时间。

本文以丰田JAT710型喷气织机为研究对象，从织机经纬向停车情况、挡车工工作效率、加工布匹品种3个方面分析影响织机了机时间的关键因素。具体的影响因素组成如图1所示。

2.1 经纬停影响因素分析

通过对金华兰溪市某纺织厂采集到的810台织机设备一个月生产情况数据进行统计后得到：织机的停车时间在织机整个织布时间内的平均占比约为9.68%，其中经、纬向停车时间在织机停车时间中的平均占比约为80.74%。

表2将数据统计维度定位至具体的10台织机，对各织机的织布米长、实际织布时间、理论织布时间、经纬停时间等数据进行收集，得到表2织机各生产时间的对比。

由表2可知，织机理论计算得到的织布时间加上经纬向停车时间二者的总和与织机实际织布时间相近，进一步论证了经、纬向停车是准确预测织机了机时间的关键因素。

2.2 挡车工工作效率影响因素分析

织机由于纱线断裂等情况暂停对织轴的继续加工后，一般由挡车人员对断裂的纱线进行重新结经，以此来恢复织机的正常运行。挡车人员的工作效率直接影响织机停车的持续时间（织机的运行效率）。

图2反应了某根织轴整个生命周期内的经纬向停车情况。

根据图2可得到，织机在对此根织轴进行织布期间，每4 h的平均经纬向停车时间为1145 s，每4 h的平均经纬向停车次数为4次。其中，可观察发现每天的中午时分（11：45）和午夜时分（23：45）以及靠近织轴即将要了机的几个时间段内的织机经、纬向停车次数与时长较高，大多会超过平均值。

通过进一步的分析，可以得到，造成此种现象的原因主要和挡车工的工作状态有一定的关系，据了解，大多数纺织企业织造车间设备都是24 h生产，工人白班、夜班轮班工作，而中午和午夜时分是最为疲惫的时间段，在这时间段内工作的工人可能会因为工作状态的原因，在处理如对纱线进行结经等需要一定专业度和手法的操作上，不能有较高工作效率的因素，而导致织机的停车时间延长；而另一个经纬停次数明显较多的时间段是在靠近织机将快要了机的几个时刻内。从图2数据可观察到，在此根织轴生命周期的最后48 h内，织机经纬停发生次数较高且集中，原因是卷绕在织轴上的纱线在将要用尽的末尾时间段里，纱线在轴上的缠绕强度不均导致织机对纱线作用的张力变化幅度较大，使纱线断纱次数增多，织机停车次数频繁。

2.3 布匹品种影响因素分析

将时间跨度从单根织轴扩大至一个品种，通过对比织机在生产不同品种过程中的经纬向停车情况，来分析针对不同布匹品种下的织机了机影响因素。

织机生产出的布匹品种不同主要由生产布匹时的产品工艺参数和所用到的纱线成分不同所决定。图3记录了同台织机针对6种不同布匹品种的生产工艺需求下，各进行15天生产后，所出现的经纬向停车情况。表3记录了图3各品种对应的工艺参数。结合表3与图3数据可发现，织机织布时的经纬向停车次数与布匹品种所需要达到的经密、纬密工艺参数大小成正比，当经密、纬密越大时，织机在织布过程中所发生的经向、纬向停车次数也会随之增多；并且织机的经、纬向停车次数多少也与所用纱线的粗细有关，当纱线的纱支参数越大，说明纱线越粗时，织机相对应在织布过程中所产生的经纬向停车次数比纱线纱支参数小、纱线细时的停车次数少。

3 LSTM循环神经网络

基于第二小节对织机了机时间的影响因素分析可知，各因素对了机时间的作用具有较强的时间关联，且针对于织机数据具有时变性这一特点，本文采用LSTM循環神经网络，对织机了机预测模型进行搭建。

长短时记忆（LSTM）循环神经网络是一种具有选择记忆功能的循环神经网络［10］，通过更新每个时刻的细胞状态，可以学习不定时间长短的时间序列信息，在一般的循环神经网络（Recurrent neural network，RNN）基础上引入了门机制用于控制信息特征的流通和损失［11］，在处理如织机了机预测此类对时间敏感的时序数据中可以防止梯度消失和梯度爆炸等问题且有较突出的数据拟合能力。LSTM网络中的每个神经元主要由遗忘门、输入门、输出门3个功能状态门以及细胞状态组成。

3.1 模型的搭建

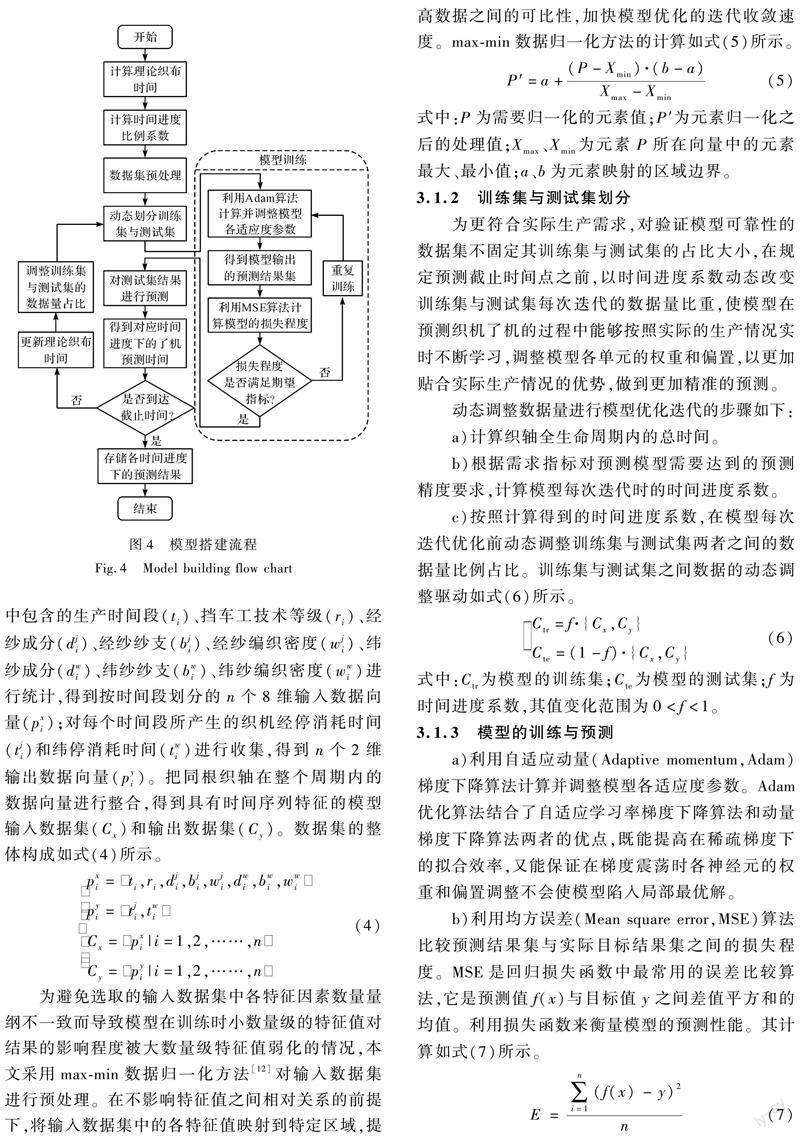
本文以LSTM循环神经网络为基础对织机了机时间预测模型进行搭建。首先，区别于直接划定训练集与测试集的数据比重，本文根据数据集包含的织机对目标织轴整体的生产时间跨度，按照所需时间精度，计算模型每次迭代优化时的时间进度系数，动态调整训练集与测试集的数据比重，做到更加贴合实际生产场景下模型可学习的训练数据量随生产时间的推移逐渐丰富的真实变化特点，全面反映模型在织轴整个生命周期内的学习和泛化能力；其次，通过定时求解剩余理论织布长度，弱化其他停因素对织机了机时间预测的影响，提高模型的预测精度。模型的搭建流程如图4所示。

3.1.1 数据集建立与预处理

本文以第二小节对织机了机时间影响因素的分析作为依据，将织轴整个生命周期进行n等分，对其中包含的生产时间段（ti）、挡车工技术等级（ri）、经纱成分（dji）、经纱纱支（bji）、经纱编织密度（wji）、纬纱成分（dwi）、纬纱纱支（bwi）、纬纱编织密度（wwi）进行统计，得到按时间段划分的n个8维输入数据向量（pxi）；对每个时间段所产生的织机经停消耗时间（tji）和纬停消耗时间（twi）进行收集，得到n个2维输出数据向量（pyi）。把同根织轴在整个周期内的数据向量进行整合，得到具有时间序列特征的模型输入数据集（Cx）和输出数据集（Cy）。数据集的整体构成如式（4）所示。

为避免选取的输入数据集中各特征因素数量量纲不一致而导致模型在训练时小数量级的特征值对结果的影响程度被大数量级特征值弱化的情况，本文采用max-min数据归一化方法［12］对输入数据集进行预处理。在不影响特征值之间相对关系的前提下，将输入数据集中的各特征值映射到特定区域，提高数据之间的可比性，加快模型优化的迭代收敛速度。max-min数据归一化方法的计算如式（5）所示。

式中：P为需要归一化的元素值；P′为元素归一化之后的处理值；Xmax、Xmin为元素P所在向量中的元素最大、最小值；a、b为元素映射的区域边界。

3.1.2 训练集与测试集划分

为更符合实际生产需求，对验证模型可靠性的数据集不固定其训练集与测试集的占比大小，在规定预测截止时间点之前，以时间进度系数动态改变训练集与测试集每次迭代的数据量比重，使模型在预测织机了机的过程中能够按照实际的生产情况实时不断学习，调整模型各单元的权重和偏置，以更加贴合实际生产情况的优势，做到更加精准的预测。

动态调整数据量进行模型优化迭代的步骤如下：

a）计算织轴全生命周期内的总时间。

b）根据需求指标对预测模型需要达到的预测精度要求，计算模型每次迭代时的时间进度系数。

c）按照计算得到的时间进度系数，在模型每次迭代优化前动态调整训练集与测试集两者之间的数据量比例占比。训练集与测试集之间数据的动态调整驱动如式（6）所示。

式中：Ctr为模型的训练集；Cte为模型的测试集；f为时间进度系数，其值变化范围为0

3.1.3 模型的训练与预测

a）利用自适应动量（Adaptive momentum，Adam）梯度下降算法计算并调整模型各适应度参数。Adam优化算法结合了自适应学习率梯度下降算法和动量梯度下降算法两者的优点，既能提高在稀疏梯度下的拟合效率，又能保证在梯度震荡时各神经元的权重和偏置调整不会使模型陷入局部最优解。

b）利用均方误差（Mean square error，MSE）算法比较预测结果集与实际目标结果集之间的损失程度。MSE是回归损失函数中最常用的误差比较算法，它是预测值f（x）与目标值y之间差值平方和的均值。利用损失函数来衡量模型的预测性能。其计算如式（7）所示。

式中：E为模型预测值与实际值比较后的损失程度；f（x）为模型计算得到的预测值，y为实际期望的目标值，n为自由度。

c）判断损失程度是否满足期望指标。将每次得到损失程度值与期望损失值进行对比，若模型当前的损失程度已经能满足期望的误差指标需求，则结束训练；若模型当前的损失程度过大，则重复训练，继续调整模型的各适应度参数，优化模型对数据的拟合能力。模型的损失程度约束如式（8）所示。

式中：Ep为模型此次预测结果值与实际结果值的误差损失程度；Ee为期望的误差损失程度。

d）预测织机的了机时间。通过计算各时间进度下的织机理论织布时间、织机加工完目标织轴所消耗的总经纬向停车时间以及织机实际已产生的经纬向停车时间，得到每个时间进度下所预测的织机了机时间。其中，各时间进度下预测的织机了机时间计算如式（9）所示。

式中：Tyci为模型在i时间进度下所预测的织机了机时间，h；Tjwi为模型在i时间进度下所预测的经纬向停车时间，h；Tlli为i时间进度下所计算得到的织机理论织布时间，h；Tsjwi为i时间进度前织机实际已产生的经纬向停车时间，h。

4 模型预测评估

本文以金华兰溪市某纺织厂采集到的数据和调研结果作为依据对模型的实际预测性能进行评估。选取了2022年2月的织造采集数据。

4.1 模型验证

将采集到的某根织轴全生命周期下的生产情况数据作为验证模型可靠性的数据集。首先，通过对织机加工织轴时记录下的开始时间（2022-02-13 02∶19∶14）与结束时间（2022-02-21 19∶47∶27）计算得到织轴的整个生产时间为209.47 h，根据预测指标的分析结果，对织轴的整个生产时间进行150等分，即令每次的了机预测迭代时间间隔控制在2 h内，细化训练迭代频率，提高预测精度，满足误差指标。模型的预测结果如图5所示。

图5中横坐标代表织机的实际织布时间进度，纵坐标代表织机的织布时间用时，红色实线标明了织机的实际织布用时为209.47 h，绿色折线为模型每次定时预测的织布时长。从图5中可观察到，随着织机生产时间的推移，模型所能学习到的织机实际生产情况数据逐渐增多，模型的整体预测趋势也逐渐向实际值逼近。图5中虚线所标记的是模型预测时间具有参考性的最晚截止时间（实际了机的前一天），结合需求指标，在截止时间之前的模型预测都有参考价值。

为验证模型的预测精度是否满足实际需求指标，将图5的實际织布时间进度范围缩小至织机织布中期（织布时间进度104.74 h）到织布结束。织机织布中期到织布结束范围内的模型预测情况如图6所示。

图6中虚线标明了在可接受误差范围内的织机织布预测时长上限（212.47 h）与预测时长下限（206.47 h）。从图6中可发现，在截止时间前两天的时间段内（织布时间进度137.47～185.47 h），模型共出现5次预测结果超出实际可接受误差范围的情况，对应的采样点分别为A-E点，与实际了机时间的差值分别为12.73、-5.07、-6.20、-21.61、6.70 h。模型存在预测结果不稳定的情况。

4.2 模型性能优化处理

对4.1小节的模型预测情况分析来看，模型的预测精度无法满足实际的需求指标。原因在于训练集与测试集数据量每次的动态调整虽然已经做到了贴合实际并不断学习，但是无法提前确定模型的最优迭代次数，模型每次对新数据量的训练集数据进行学习时会出现欠拟合或过拟合的情况，导致模型在学习过程中错过或没有达到最小损失值，使模型的预测性能不稳定。

通过以上分析，本文提出在模型训练时设置动态损失变化阈值的方式，以提高模型的泛化能力。动态设置损失变化阈值的流程如图7所示。

设置动态损失变化阈值的具体步骤如下：

a）对模型前50次迭代训练中大于零的损失变化差值进行记录。记录下的损失变化差值计算如式（10）所示。

式中：Δe为记录下的损失变化差值，其值大于零；ec为此次模型训练后的损失值；el为前一次模型训练后的损失值。

b）计算当前训练集所对应的损失变化阈值，即计算记录下的损失变化差值的平均值，损失变化阈值的计算如式（11）所示。

式中：Goffset为损失变化阈值；Δei为第i个损失变化差值；n为记录下的损失变化差值个数。

c）利用计算得到的损失变化阈值，寻求合适的迭代次数与损失值。若模型此次训练得到的损失值大于模型前一次训练所得损失值与损失变化阈值之和，则模型训练结束，将模型前一次的训练结果作为最终训练结果，即模型训练结果满足如式（12）时模型训练结束。

为验证设置的动态损失变化阈值对模型预测性能的提升，再次利用4.1小节的验证数据集，将模型优化前后对数据集训练迭代时的损失程度进行对比。图8展示了模型优化前在对时间进度61%数据量下的训练数据集进行固定250次训练迭代时的损失程度变化，以及模型优化后根据损失变化阈值动态确定迭代次数和损失值的数据变化情况。图8虚线为模型优化前的训练损失程度变化情况，可观察到模型在第71、100、102、187、190次迭代训练时的损失值较小，分别为10.3、10.5、10.4、9.2、9.1、13.6，而在最后一次迭代训练中模型对应损失值为13.6，并不是整个迭代训练中属于较好的一次，且设置过多的迭代次数也存在着模型训练耗时、耗资源的问题。

图8实线所标明的是模型优化后对前50次数据计算得到的损失变化差值，分别为0.021、0.076、1.136、0.026、2.069、0.880、1.120、0.124、1.230，则损失变化阈值为0.74。利用计算得到的损失变化阈值，确认模型的最终训练结果在第71次，模型的最终训练损失值为10.3，如图8中的e点所示。虽然根据所示变化偏置算法所得到的最终训练结果不

是模型在250次训练中最好的，但也是在结合了模型训练耗时与模型训练准确度两方面因素考虑下属于较好的一次。

图9为模型优化前后对4.1小节的验证数据集进行训练迭代时的整体训练耗时和损失程度对比图。图9（a）为训练耗时对比图，其中，淡红色为模型优化前的每次训练耗时，总耗时为15.70 h，平均耗时为376.65 s，可觀察到对模型设置固定250次的训练迭代次数情况下，随着时间进度的推移、模型的训练数据量变大，模型对每一次训练集进行训练所需要的消耗时间也逐渐增大；深蓝色为模型优化后所对应的训练耗时，总耗时为3.21 h，平均耗时为77.67 s，在相同数据量的情况下，模型的训练耗时明显下降；图9（b）为模型优化前后的损失程度对比图，图中淡绿色为模型优化前的每次训练损失程度，平均损失程度为11.55，深紫色为模型优化后的损失程度，平均损失程度为3.21。

可明显观察到优化后的模型在训练耗时和损失精度上都得到了很大的提升。

将优化后的模型用于对4.1小节同根织轴的了机时间进行预测，图10（a）展示了织轴整个生命周期内不同时间进度下的模型了机时间预测情况。图10（b）为模型在织机织布中期（织布时间进度104.74 h）到织布结束局部时间范围下的了机时间预测情况，从图10（b）中可观察到模型在截止日期的前两天时间内，预测结果已经逼近于实际值，且预测结果在允许误差范围内始终保持稳定。

为验证模型的泛化能力，随机挑选8组数据进行验证，其结果如表4所示。

从表4中可观察到，在预测截止时间的前30 h、前24 h、前18 h、前12 h、前6 h，模型的预测值与实际值之间的平均误差分别为0.88、0.84、1.52、1.51、0.99 h。模型的预测情况满足指标要求。

5 结 论

本文对织机理论了机时间与实际了机时间进行对比后发现，织机在织布过程中不定时出现的停车而额外对生产增加的消耗时间是影响准确预测织机了机时间的关键因素。通过对织轴的整个生命周期内出现的织机经、纬向停车次数和持续时间进行分析，得到影响织机了机时间的数据集，将LSTM模型应用到织机了机时间预测的问题中，提出动态设置损失变化阈值的方法对预测模型进行优化，从模型训练时间和损失程度两方面对模型优化前后的结果数据进行对比，验证方法具有可行性。得出结论如下：

a）对织机实际生产时出现的各类停车状态消耗时间进行统计，得到织机的停车时间在织机织轴的整个织布时间内的平均占比约为9.68%，其中经纬向停车时间在织机停车时间中的平均占比约为80.74%，说明经、纬向停车对织机的了机预测起到关键的影响作用。

b）通过对实验数据的验证，发现在预测截止时间的前两天时间内，本文提出的LSTM预测模型的预测结果与实际值之间的平均误差范围为0.84 h至1.52 h，满足实际生产时的指标要求。

参考文献：

［1］黄锦波，祝成炎，张红霞，等.基于剑杆织机改造的三维间隔机织物工艺设计［J］.纺织学报，2021，42（6）：166-170.

HUANG Jingbo， ZHU Chengyan， ZHANG Hongxia， et al. Design of three-dimensional spacer fabrics based on rapier looms［J］. Journal of Textile Research， 2021，42（6）：166-170.

［2］梅自强.纺织辞典［Z］.北京：中国纺织出版社，2007：445.

MEI Ziqiang. Dictionary of Textiles［Z］. Beijing： China Textile&ApparelPress， 2007： 445.

［3］王守泽，张五九.一种基于卷径变化预测织机了机的方法：CN110331503A［P］.2019-10-15.

WANG Shouze， ZHANG Wujiu. A method for predicting the weaving machine based on the change of winding diameter：CN110331503A［P］. 2019-10-15.

［4］沈春娅，雷钧杰，汝欣，等.基于改进型NSGAⅡ的织造车间多目标大规模动态调度［J］.纺织学报，2022，43（4）：74-83.

SHEN Chunya， LEI Junjie， RU Xin， et al. Multi-objective large-scale dynamic scheduling for weaving workshops based on improved NSGAII［J］.Journal of Textile Research， 2022，43（4）：74-83.

［5］郭广慧，李春梅.基于移动终端的织机运行数据监测系统开发［J］.纺织科技進展，2017（6）：15-16.

GUO Guanghui， LI Chunmei.Development of loom runing data monitoring system based on mobile terminal［J］.Progress in Textile Science & Technology， 2017（6）：15-16.

［6］罗东升.织机实时织造信息管理系统的研发与应用［D］.杭州：浙江工业大学，2014：18-25.

LUO Dongsheng. Development & Application of Mana-gement System for Real-time Loom Information［D］. Hangzhou： Zhejiang University of Technology， 2002：4-8.

［7］郑宝平，蒋高明，夏风林，等.基于模型预测的经编送经动态张力补偿系统设计［J］.纺织学报，2021，42（9）：163-169.

ZHENG Baoping， JIANG Gaoming， XIA Fenglin， et al. Design of dynamic tension compensation system for warp knitting let-off based on model predictions［J］. Journal of Textile Research， 2021，42（9）：163-169.

［8］张晓侠，刘凤坤，买巍，等.基于BP神经网络及其改进算法的织机效率预测［J］.纺织学报，2020，41（8）：121-127.

ZHANG Xiaoxia， LIU Fengkun， MAI Wei， et al. Prediction of loom efficiency based on BP neural networkand its improved algorithm［J］. Journalof Textile Research， 2020，41（8）：121-127

［9］周亚勤，汪俊亮，鲍劲松，等.纺织智能制造标准体系架构研究与实现［J］.纺织学报，2019，40（4）：145-151.

ZHOU Yaqin， WANG Junliang， BAO Jinsong， et al. Research and implementation of standard system architecture of textile intelligent manufacturing［J］. Journal of Textile Research， 2019，40（4）：145-151.

［10］刘树鑫，高士珍，刘洋，等.基于LSTM的交流接触器剩余寿命预测［J］.高电压技术，2022，48（8）：3210-3220.

LIU Shuxin， GAO Shizhen， LIU Yang， et al. Residual life prediction of AC contactor based on LSTM［J］. High Voltage Engineering， 2022，48（8）：3210-3220.

［11］黄建华，钟敏，胡庆春.基于改进粒子群算法的LSTM股票预测模型［J/OL］.华东理工大学学报（自然科学版），2021：1-12［2022-09-13］.DOI：10.14135/j.cnki.1006-3080.20210616001.

HUANG Jianhua， ZHONG Min， HU Qingchun， et al. LSTM stock prediction model based on improved particle swarm optimization algorithm［J/OL］. Journal of East China University of Science and Technology， 2021：1-12［2022-09-13］.DOI：10.14135/j.cnki.1006-3080.20210616001.

［12］姚桂國，梁金祥，左保齐.基于网格的织物图像拼接技术［J］.纺织学报，2012，33（2）：46-49.

YAO Guiguo， LIANG Jinxiang， ZUO Baoqi， et al. Fabric image mosaicing technology based on grille［J］. Journal of Textile Research， 2012，33（2）：46-49.

Abstract： Loom production mainly refers to the process of weaving weft and warp on the weaving axis into cloth in vertical and horizontal directions. When the yarn of the loom axis ， the axis， drop wires， heald， reed and warp yarn need to be cleaned from the loom. This process is called the loom changing the axis. If the axis is changed too early， the yarn material of the weaving axis will be wasted. If the warp axis is not set in time， too long stagnation of machine and insufficient length of remaining warp will cause problems such as inability to knot the new axis. Accurate prediction of warp-out time， timely arrangement of personnel for warp threading， warp knotting and axis change， so that the new weaving axis can be put into production in time， which has an important effect on improving the production efficiency of weaving.

When calculating the looms warp-out time by using the pre-set static parameters of planned production， the deviation between the theoretical calculation value and the actual value is too large. Aiming to solve this problem， a looms warp-out time prediction method based on LSTM recurrent neural network proposed. Based on the analysis of the factors affecting the loom warp-out time from three aspects： the warp and weft stop of the loom， the working efficiency of personnel and the variety of cloth processed， a data set of loom production with time series characteristics s constructed. The prediction of the model in the whole life cycle of the weaving axis was dynamically adjusted by setting the time schedule coefficient， and the performance of the model was optimized from two aspects of loss degree and training time. On this basis， propose to set the dynamic loss change threshold to determine the optimal number of iterations of the model under different training data to improve the generalization ability of the model. Finally， the statistics of the consumption time of all kinds of stop states in the actual production of the loom re carried out， and the conclusion s drawn that the average percentage of the loom's stopping time in the whole weaving time of the weaving axis s about 9.68%， and the average percentage of the warp and weft stopping time in the loom's stopping time s about 80.74%， which shows that the warp and weft stopping plays a key role in the prediction of the warp-out time. Through the verification of the experimental data， it is found that the average error between the predicted results of the model proposed in this paper and the actual values is 0.84 h to 1.52 h in the two days before the deadline of the prediction of the warp-out time， which meets the index requirements of actual production.

The accurate prediction of warp-out time by intelligent prediction model and the analysis of the relationship between looms warp-out time and various influencing factors can provide inspiration for optimizing weaving scheduling and adjusting weaving production process， so that workshop personnel can reasonably control the material processing progress and ensure uninterrupted and efficient production between weaving links. The research results can provide reference suggestions for the intelligent transformation of traditional textile industry.

Keywords： looms warp-out time LSTM recurrent neural networktime serieswarp and weft stopweaving axisdynamic loss change threshold