基于知识空间理论的微积分关键学习路径描述

陈东晓 李进金

摘要：文章以大一学生的学习成绩和平时测验为基础，通过关键学习路径的描述研究微积分预前知识学习对微积分成绩的影响。通过两次测试的分析，提取每次测试的知识状态，构建知识状态树来确定学生的关键学习路径，并且通过知识结构和关键学习路径来比较两种不同教学方式班级学生的真实学习状态，表明了微积分预前知识学习的重要性。研究发现，通过知识空间理论识别教师期望学生拥有的知识结构与学生在测试中展示的真实知识结构之间的差异，为教师调整所教知识概念的顺序提供指导，并根据预期的掌握水平定制教学计划。关键词：知识空间理论；知识状态；微积分教学；关键学习路径 中图分类号：G642

文献标识码：A

文章编号：1002-4107（2023）04-0028-04

对理工科和经管类专业的大学生来说，“高等数学”是大学阶段一门非常重要的通识基础课。令人担忧的是，“高等数学”考试的不及格率比较高，学生学习微积分的兴趣明显下降，学生将“高等数学”视为一门难以理解的课程。数学成为一门难学课程的一些重要因素是其概念的抽象性、大量符号公式、大量计算和严格证明推导。由于部分学生在初等教育时未能掌握基本的数学概念，形成错误的观念，因此阻碍他们在日后的教育中掌握更复杂的数学概念[1]。另外，除了学科本身的难度和所研究问题的内在复杂性外，数学学习中的问题有时是由于指导不充分，教师没有及时充分了解学生所掌握的知识状态。对于教师来说，按照自己思维来讲解知识点是不够的，要从初学者的角度来考虑学生学习的过程和困难。而教师期望的教学效果与学生实际学习效果之间的差距可以用学生成绩来解释，可以通过知识空间理论来研究从教师预期的知识结构和真实的知识结构之间差异，研究学生真实的学习路径。

知识空间理论（Knowledge Space Theory，简称KST）由杜瓦尼翁（Doignon）和法尔马涅（Falmagne）提出，是教育心理学的组成部分之一[2-3]。由于其在认知诊断方面的突出表现，知识空间理论已经在国外得到了广泛的应用，特别是在线教育评测和智能教学方面[4-5]。本文针对两组同一本科专业的学生，通过知识空间理论分别构建了他们在测试中展示的真实知识结构以及关键学习路径，对两组学生的知识结构和关键学习路径差异进行分析，表明了微积分学前辅导是必要的，对于学生成绩的影响较大，进而对微积分教学内容设计提供一些有益的建议。  一、知识空间理论

大多数传统知识评价使用闭卷考试等方式来评估学生对数学概念的理解。由于评估的方法多种多样，考虑到学生需要掌握知识的深度和广度，很难知道哪些方法是有效的。知识空间理论（KST）以对评估工具的反应进行结构分析为原则，是一种在给定情境下表示学生知识的形式化方法或模型，所创建的结构提供了与学生知识相关的细节，以及获取这些知识所采用的学习路径。作为一种评估工具，KST可以告知教师一组学生在教学期间掌握不同概念的顺序。知识空间理论引入了数学建模和评估学生知识结构的技术，为跟踪学生成绩和指导学习过程提供了新的可能性。杜瓦尼翁（Doignon）和法尔马涅（Falmagne）将KST作为“正式描述给定知识领域结构的手段”[2]。知识结构是通过学生能够正确回答的问题来描述的，每一个学生对给定作业或测试的回答成为整体结构的一个子集，学习路径可以从尝试的空集（无正确）到完整问题集（全部正确）。

一般来说，一个知识域Q是由一组有限指定的问题构成的集合，这组问题包括学生在给定评估中可以解决或可能无法解决的问题。每个学生都可以用他自己的知识状态来描述，而知识状态是由他们正确回答的所有问题所构成Q的子集，所有的知识状态（至少包含空集和全集）组成了一个知识结构K。如果K中任何两个知识状态K1和K2，K1∪K2也是K中的一个知识状态，这意味着知识结构K是并封闭的，称K为一个知识空间。而满足学习的顺畅性（Smoothness）和学习的持续性（Consistency）的知识空间称为学习空间[3]。

概率知识结构是将局部独立模型方法应用到知识空间理论中，其主要考虑两种实际情形：一是被试个体或群体的知识状态频率，二是考虑被试者在回答问题过程中由于粗心错误和幸运猜对的概率。选择这些知识状态的方法是使用χ2分析，统计量χ2基于实际响应状态和预期知识状态之间的差异，通过添加和减去最多的响应状态，以最小化χ2值形成一个哈斯图，其中每个状态有一个前状态和一个后状态，而每个连续的状态比前一个状态正好多出一个问题。由此产生的知识结构可以揭示学生用来学习的几种学习路径。学习路径定义为“知识状态的最大序列，允许学习者从空集逐步遍历知识结构或知识空间，直至完整的问题集Q”。学习者从空集开始，到完全掌握状态Q，学习路径可以被绘制出来。通过描述每个知识状态的概率值代表班级中处于知识状态学生的比例，从最大概率的知识状态出发，最佳或最可能的学习路径被确定为由响应状态组成的关键学习路径。一旦建立了关键学习路径，就可以将每个学生与一般课堂表现以及最佳表现（Q）进行比较。

KST可以为高等数学教学作出重大贡献，通过了解学生的知识结构克服教师、教科书和教学大纲之间关于概念组织和适当教学策略的差异。近年来，国内外学者有的针对中学生进行化学课程学习能力提升的研究[6-8]，有的基于知识空间理论进行图书馆阅读推广平台的建设[9]，而针对本科生学习效率或能力提升的知识空间理论研究还不多见。本文使用数据分析方法构建学生的真实知识空间，获取关键学習路径，并比较两组研究对象的关键学习路径差异，分析借助于线上辅助基础知识教学对微积分学习的帮助效果，前期学习对后期学习的影响，为微积分教学研究提供了有效方法。   二、研究方法

（一）研究对象

本研究的参与者是选修“微积分学”的工商管理类2020级大一学生。“微积分学”是华侨大学本科经济管理类大一新生的一门必修课，分两学期完成教学，每学期4学分。在研究开始的时候，选择的研究对象是由同一位主讲教师教微积分课程的两个班级，其中一个班级选为实验组（也称为“辅导班”），另一个班级为对照组（也称为“正常班”）。学期初，学生通过在线学习软件接受了一次“学前知识检查”——一次由20道基本计算题组成的测验，每道题都涉及到微积分所必需的基本概念或公式[10]。考前测验衡量的是学生学习微积分前的基础知识，以便于结合学生的学习弱点给与相应基础知识辅导。

整个学期，这两个班级学生都完成了常规教学课程，包括练习家庭作业、3次在线章节测验、期中测试和期末考试。所有这些都是对课堂上教授微积分内容的测试。实验组还安排了有助教的在线辅导课，不断鼓励该组学生积极参加这些在线讨论，侧重于根据学生的具体学前基础知识（中学学习过的相关知识）的辅导，诸如三角函数、反三角函数、幂函数、指数函数等定义域和值域、图像，以及一些常见的初等公式。这些辅导课是由研究生助教进行评分的，他们还负责每次家庭作业的批改，主讲教师也参与学生在线学习讨论并根据学生情况决定课堂讲解和相应的讲解。

（二）研究流程和数据收集

本文使用了三种工具来收集数据：（1）平时作业；（2）微积分期中测试和期末考试；（3）在线学习通测验。在线测验中，把一些相关知识点设计为单选或多选选择题和是非判断题，以获得微积分学前和学习过程中基础知识方面的数值分数。考试由任课教师和研究生助教一起进行评分，助教还负责每周课后作业的批改及评定等级。为了明确微积分期中测试和期末考试评分的一致性，学生参加学校对经管类大一新生统一的公共数学考试，在规定时间内完成测试，统一由任课教师制定评分标准并批改试卷。

（三）使用KST进行数据分析

采用知识空间理论（KST）分析并提取关键学习路径，以评估两个不同教学方式微积分课程的表现：实验组和对照组。实验班微积分课程包括以建构主义的方式教授必要的学前积分知识，使用基于问题驱动的学习方法，比传统的微积分课程要求多次知识在线小测。在实验班教学中，运用多种学习条件，结合问题驱动教学方法，可以创造一个更有利于有意义学习的学习环境。而对照班按传统教学方法，通过教师课堂讲解教学内容和复习，学生课后做习题来完成微积分教学。通过本次实验比较，进一步说明微积分学习不能只靠观察和倾听，而应该通过不断实践来学习。

通过一个学年两次测试的数据研究，分别获得了关于求导与求积分方面的知识状态和知识哈斯图来确定这些关键学习路径。例如，根据第一学期期末考试，适当选取7道关于导数方面的知识点试题作为测试一进行实验数据统计，包括（1）极限四则运算；（2）无穷小比较；（3）函数连续性；（4）导数的定义；（5）高阶导数；（6）求导法则；（7）导数的应用。

为了处理这些数据，根据获得的测试结果把每个学生的回答情况记为一个响应状态，也称为知识状态。记每个问题的最高分（完全正确答案）为“1”，低于最高分值（错误或部分正确答案）的点记为“0”。例如，学生对问题1到问题7的知识状态为“1010110”，表示该学生在第一、第三、第五和第六问题回答完全正确，而其他问题做错或者没全对。具体步骤如下。首先，统计所有学生的真实知识状态及其对应的学生人数，并通过知识空间理论的并封闭性质分别给出实验组和对照组学生的知识空间，而得到的知识空间中知识状态并不都是真实学生状态，而对于假定的知识状态人数记为0，得到一个所有测试者的知识状态表。接着，通过得到的知识空间使用Graphviz软件画出知识空间哈斯图，并利用知识空间的独立概率模型知识，由python软件设计算法计算出每个知识状态的概率。最后，通过每一状態层概率最大的知识状态描绘出关键学习路径。根据以往研究，本文中实验数据假设对于幸运猜测和粗心错误的概率估计都是10%。

例如，测试1中实验组的数据，其中q1到q7分别表示7个相关问题，实验组共39个学生，但实际只有21种知识反应状态，而形成的知识空间却有52个知识状态，有31个是假定的知识状态。测试1中实验组有3个学生的知识状态是“1010010”，而该知识状态概率是0.048。

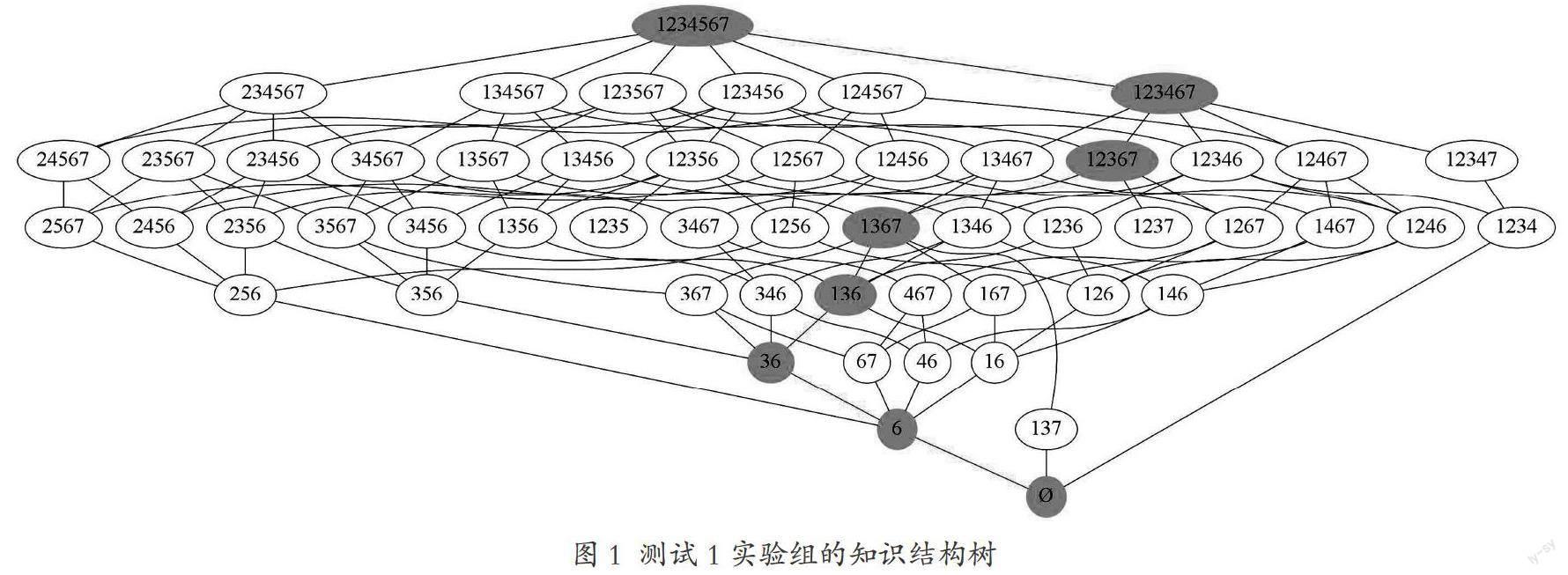
图1是测试1中实验组的知识状态树，图中以完成问题的编号来描述，即对应知识状态“1010010”记为“136”，其中黑色部分是通过知识状态概率得到的关键学习路径。图2是测试1中对照组的知识状态树，其中黑色部分是通过知识状态概率得到的关键学习路径。

我们通过选择每一层中人数最多、问题数最少的知识状态作为关键学习路径的节点，然后把这些节点连接起来形成关键学习路径。例如，实验组的测试2的关键学习路径是6→3→1→7→2→4→5。而与这一关键学习路径相关的问题是：求导法则→函数连续性→极限四则运算→导数的应用→无穷小比较→导数的定义→高阶导数。

同样，我们也通过收集实验数据画出测试1中对照组的知识状态树图2。

从测试1中，可以发现实验组的知识结构树与对照组的知识结构树具有相似的无组织特征。实验组在图1中，第四、第五和第六级有大量的知识状态，在这三个层次上共有30个知识状态，占全部知识状态的61%，这说明知识结构树不是很有组织。我们注意到对照组的学习路径：6→1→7→2→3→5→4，对应题项：求导法则→极限四则运算→导数应用→无穷小的比较→函数连续性→高阶导数→导数的定义。很明显，与实验组的关键学习路径是不一样的，主要的区别是问题3的顺序。问题3是关于函数的连续性问题，主要考题是关于间断点分类，实验组明显在求左右极限方面表现得更为好些。关于问题4和问题5，一个是关于导数的定义，另一个是高阶导数，很明显对于两组人来说都是一个难题，所以这两个问题回答全对的学生是最少的，从关键学习路径看它们都放在最后两个。关于问题6，大部分学生在中学就学习过求导数相关知识，较为熟悉，所以这个问题回答全对最多，而这也是他们学习路径最开始的选择。

类似的，笔者对另一次期末考试（测试2）进行了分析，试卷共有16道题，适当选择其中6道关于积分方面问题作为测试题：（1）不定积分基本公式；（2）不定积分计算方法；（3）微积分基本公式；（4）定积分计算；（5）定积分的几何应用；（6）二重积分计算。

对于测试2，使用相同的方法和过程生成知识状态，并为实验组（图3）和对照组（图4）创建知识结构树。笔者发现实验组测试2的关键学习路径：1→2→5→3→4→6，也就是：不定积分基本公式→不定积分计算方法→定积分的几何应用→微积分基本公式→定积分计算→二重积分计算。对实验组测试2的知识结构树进行了仔细的比较研究，知识结构树总共只有六个水平，没有学生在测试中只正确回答了一个问题，并没有存在第二层次的知识结构（只答对一个问题的知识状态）。笔者认为这个知识结构树更有组织性，因为它总共只有18个知识状态。此外，该知识结构树的关键学习路径显示了更为贴合教学内容的教学顺序。

同样，测试2对照组的知识结构树也显示出比测试1的知识结构树更好的组织。知识结构树有7个层次，30个知识状态。知识状态树的第四级和第五级包含了大多数的知识状态，其中约57%的知识状态出现在这些级别上。对于测试2对照组的关键学习路径与实验组也有所不同，即2→1→6→5→3→4。相应的问题是：不定积分计算方法→不定积分基本公式→二重积分计算→定积分的几何应用→微积分基本公式→定积分计算。对照组和实验组在关键学习路径上的主要区别在于问题6的顺序。

三、研究结果和分析

总体而言，测试1是第一学期的期中考试，已经经过半学期的教学实验，实验组在微积分预前学习上要求更高，提供更多的学习帮助，所以测试1的知识结构树在对照组和实验组之间已经有所不同，实验组表现得更为混乱些，不如对照组的知识结构简单。而测试2是在第二学期期末，测试2中实验组的知识结构树在关键学习路径上显示出更大的变化，从而表明学生对概念的理解更为深入。

在比较测试1的知识状态时，笔者发现对照组比实验组少了8种知识状态，而在测试2中，对照组的知识状态比实验组反而多了12个。两个班级从第一次测试到第二次测试的知识状态数量都有很大的减少：实验组在测试1的知识状态数是52个，但是测试2只有18个；对照组的知识状态从测试1的44个减少到测试2的30个，减少的幅度较小。即从知识结构上看，实验组的知识结构变化较大，且在测试2中的知识结构简单体现出较有组织性。对于实验组来说，在学生知道如何解决相对简单问题的情况下，也许教师需要花更多的时间来解释如何解决高级衍生问题。

此外，测试1的知识结构树显示，两个班的关键学习路径都是从问题6（求导及求导公式）开始的，这是因为中学已经学习了求导公式。实验组的知识结构树关键学习路径也显示，学生在关键学习路径上完成微积分问题的时间比对照组要快。实验组的关键学习路径问题的顺序为4（导数定义）和5（高阶导数），即为了正确地完成问题5，学生需要准确地回答问题4。实验组按照正确的顺序回答这两个问题，而对照组则按照相反的顺序回答这两个问题。这个结果可能意味着对照组不是在猜测，就是混淆了几个基础概念。比如，对照组的学生不能正确应用导数定义解决三角函数应用部分的问题4。

实验组测试2的关键学习路径表明，该班在完成问题1和问题2时非常成功。这两个问题涉及不定积分基本公式，然后使用问题1的结果来解决问题2的不定积分计算。实验组的关键学习路径还表明学生按照正确的顺序完成问题3和问题4。为了正确地完成问题4，学生首先要正确地解决问题3，其中包括利用微积分基本公式求定积分，而问题4是定积分计算需要以基本公式为基础，加上换元法和分部积分法来计算。另外，对于对照组，测试2的关键学习路径表明，学生在问题1和问题2上不仅顺序相反，而且被问题3分开；虽然问题3和问题4是按照正常顺序，但在关键学习路径上被问题1分开；而在问题4（定积分计算）和问题6（二重积分计算）上顺序相反，实际问题体现了对照组在预前知识上的不扎实。有趣的是，对照组在测试2中难度比较大的问题6得分上高于实验组。这支持了这样的假设，即对照组可能已经记住了如何进行计算二重积分和定积分，但是没有很系统地学习微积分的预前知识。随着整个学期微积分课程的进展，由于预期知识的不足，对照组的关键学习路径继续以相反的方式描述关于微积分学习内容的顺序。    四、结论

这项研究的结果表明了知识空间理论的应用提供了一个有效的方法来表示一组学生微积分知识领域的结构，进而得到他们的关键学习路径。利用知识空间理论，绘制学生在学微积分前的知识结构图，进而可以通过技能函数描述不同班级学生在不同干预水平下的知识结构和状态，并基于这种知识结构，在课程评估中发现关键的学习路径。这种方法在评估学生的技能和知识方面是有意义的，它为提高学生成绩所需的潜在补救措施提供了有用的见解。

对学生关键学习路径的研究支持这样一个结论：在微积分中建立坚实的学前基础是学生学好微积分的必要条件。知识状态和关键学习路径的连续性反映了学生对微积分基本概念的理解，并提出了一种系统的补充或者补救方法。笔者认为，对不同评估策略的关键学习路径的调查将使教师能够生成描述学生获得概念的知识结构树，为教师调整所教概念的顺序提供指导，并根据预期的掌握水平定制教学。

参考文献：

[1]潘兴侠，郭琦茹，林楠.本科生高等数学成绩影响因素调查——基于logistic回归模型的分析[J].大学数学，2021（4）.

[2]Falmagne J.C.，Koppen M.，Villano M.，et al..Introduction toKnowledge Spaces[J].Psychological Review，1990（2）.

[3]Falmagne J.C.，Doigon J.P..Learning Space[M].Heidelerg：Springer-Verlag，2011：45.

[4]Lakshminarayan K..Theoretical and empirical aspects of somestochastic learning models[D].University of California，Irvine，1995.

[5]Lee S.，Belkasim S.，Chahine I.C.，et al.. A Web Application forthe Knowledge Space Theory Analysis：KST Web[J].Interna-tional Journal of Engineering Research and Technology，2014（9）.

[6]麥裕华，何庆辉，肖信.基于知识空间理论的高中生科学原理学习分析——以氧化还原反应为例[J].化学教育，2018（19）.

[7]何庆辉，麦裕华.基于知识空间理论的高一学生离子反应关键学习路径[J].化学教学，2018（7）.

[8]Segedinac M.，Horvat S.，Rodi D. D.，et al..Using knowledgespace theory to compare expected and real knowledge spacesin learning stoichiometry[J].Chemistry Education Researchand Practice，2018（19）.

[9]刘欣怡，徐丽芳.数字教育出版自适应智能教学与评估系统研究——以麦格劳·希尔的ALEKS为例[J].出版参考，2020（6）.

[10]杨淑辉，张妍.在线作业平台对学生成绩影响的差异性分  析[J].大学数学，2020（2）.