随机风沙冲蚀叶片涂层的数值模拟研究

2023-05-30刘士毅岑海堂刘光友

机械科学与技术 2023年5期

刘士毅，岑海堂，刘光友

（内蒙古工业大学机械工程学院，呼和浩特 010051）

中国幅员辽阔，但其地貌复杂、各地区气候存在很大差异。西北华北地区沙化严重，并形成中国八大沙漠[1-3]、东北冰雪多、东南沿海地区暴雨频发，然而中国的风能资源又主要聚积于此，所以风力机的工作环境差，常年遭受风沙冲蚀、阳光曝晒以及极端温差作用[4]，导致叶片涂层损伤严重、修复困难、维修成本高，严重影响叶片的气动性能以及风力机组的输出功率，极大地降低了风力机的经济性[5-7]。张永等[8]基于自制试验台，采用气流挟沙喷射法研究了风沙作用下风力机叶片涂层冲蚀特性，进而得到涂层冲蚀磨损量与冲蚀速度的关系，并建立了涂层冲蚀磨损程度的评价公式。徐伟胜等[9]对航空发动机叶片表面硬质涂层受沙粒高角度冲击而出现裂纹的问题进行了研究，通过实验模拟硬质颗粒以高角度重复冲击TiN/Ti 硬质涂层，并研究了调制比、层数结构对硬质涂层冲击损伤的影响，结果表明硬质颗粒重复冲击作用引起涂层疲劳剥落和圆周疲劳裂纹的产生。戴丽萍等[10]针对含沙气流对风力机叶片冲蚀作用问题进行了数值模拟仿真，并基于实验数据建立了玻璃钢材料的沙蚀冲蚀率模型，进而基于风力发电机叶轮三维流场及沙粒运动特点，计算得到了叶片表面在各工况下的冲蚀率，结果表明叶片中、外叶展前缘区域冲蚀损伤最为严重。本文基于已有试验结果，利用EDEM 与Fluent 耦合进行风沙冲蚀进行数值模拟，得到随机载荷数据，并对叶片涂层进行有限元分析，为涂层疲劳强度计算和后期维护提供理论基础。

1 风机叶片涂层三维模型

本文参照3 MW 风力机结合Glauert 法确定风机主要参数，通过气动分析软件Profili 和三维建模软件UG 建立涂层三维模型。

该风机叶片模型中，风轮直径D= 90 m，取轮毂半径rhub= 1.5 m，则叶片长度L= 43.5 m，风轮转速n= 19.3 r/min，沿叶片展向选取6 个翼型截面，其占位分别为0.17、0.42、0.57、0.75、0.95 和1。本文结合风力机叶片专用翼型的相关特性选用FX77-343、S818、S830 及S831 这4 种翼型，并由气动分析软件Profili 计算得到各翼型在最大升阻比时的攻角和升力系数，并通过葛劳渥设计法的相关公式计算得到叶片各翼型的攻角αi、入流角φi、安装角βi及弦长ci等建模参数，如表1 所示。

表1 叶片建模参数

通过Profili 生成上述各类型翼型轮廓数据，将数据导入UG 建立各翼型曲线串，建立的叶片三维模型，如图1 所示；叶片表面建立的涂层三维模型，厚度为2 mm，如图2 所示。

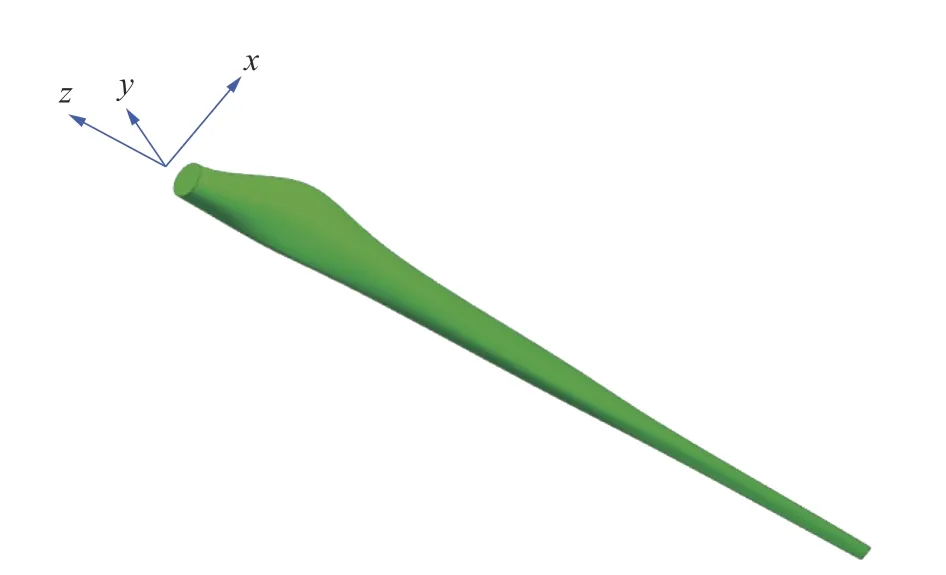
图1 叶片三维模型

图2 涂层三维模型

2 随机风速模型建立

本文以内蒙古地区为例，对大型风电场风力进行风速数据监测如图3 所示。得到实测风速样本总均值和总方差分别为12.34 和5.24。

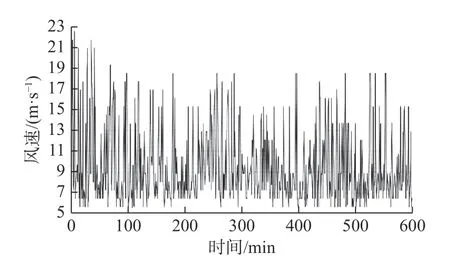
图3 内蒙古某大型风电场实测风速

自然风受大气压强的影响而瞬息万变，导致风速的变化具有明显的随机性，工程实践表明威布尔分布是目前最能描述自然风速的数学模型，其结果与风场实际监测数据较为吻合，被广泛应用于风能相关领域的计算中。

求解方程为：

式中：V为风速；U为[0,1]之间的随机数。

对于给定样本的均值和方差，求解威布尔分布的形状参数k和尺度参数c[11]，即

最后可得到基于威布尔分布模型的风速数学为

通过MATLAB 自带随机函数可得威布尔风速模型概率密度如图4 所示，威布尔风速模型的分布如图5所示，威布尔风速模型的随机风速时间序列如图6 所示。

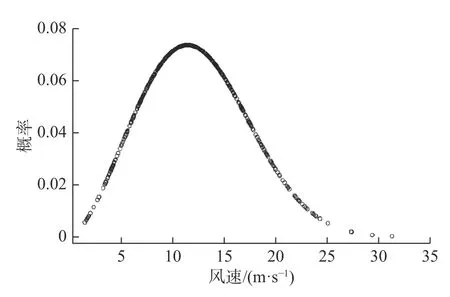
图4 威布尔风速模型的概率密度图

图5 威布尔风速模型的分布图

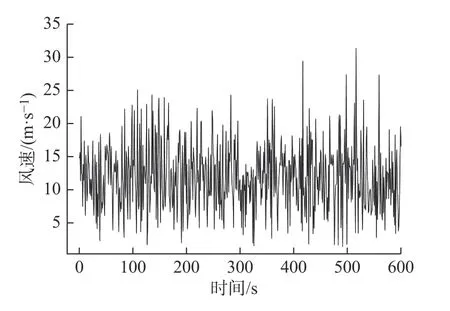
图6 威布尔风速模型的时间序列图

3 随机风沙冲蚀仿真

由于自然风速不可避免的呈威布尔分布随机变化，因此对于内蒙古地区服务于沙尘环境下的风力机叶片涂层耐久性的研究，应充分考虑变量（风速大小、沙粒直径等）的随机性，进而生成叶片涂层及流体域的三维网格模型、离散元分析软件EDEM 计算沙粒数据以及流体分析软件Fluent 计算流场数据，得到随机风沙冲蚀叶片涂层的随机载荷数据。

3.1 EDEM 和Fluent 耦合仿真的基本流程

Fluent 自带的离散项也能进行数值模拟仿真，但是其限制离散项体积分数不超过10%，只能进行稀疏的低浓度两项流的仿真，这为工程实例的仿真带来极大的不便，因此本文通过Fluent 与EDEM 耦合仿真，以此实现对风沙两项流冲蚀叶片涂层的模拟仿真。基于拉格朗日耦合仿真的基本思路可得到EDEM 与Fluent 耦合仿真的基本流程，如图7 所示。

图7 EDEM 与Fluent 耦合仿真流程

3.2 网格划分

创建计算模型流体域，设置流体域的入口边界inlet、出口边界outlet、壁面wall 以及流固耦合面FSI，设置旋转的流体进行旋转速度与方向风机叶片的旋转方向为（0，0，1），旋转速度为19.3 r/min。建立流体域四面体网格，其节点为270 136，单元数为1 154 386。网格划分后的流体域模型如图8 所示。

图8 流体网格划分

3.3 随机风沙冲蚀仿真

本文以内蒙古某地为例，其沙粒直径分布及其含量分布如表2 所示。为了最大限度贴合实际工况，本次模拟仿真分析中采用的沙粒直径数据直接参照表2 选取，结果如表3 所示。

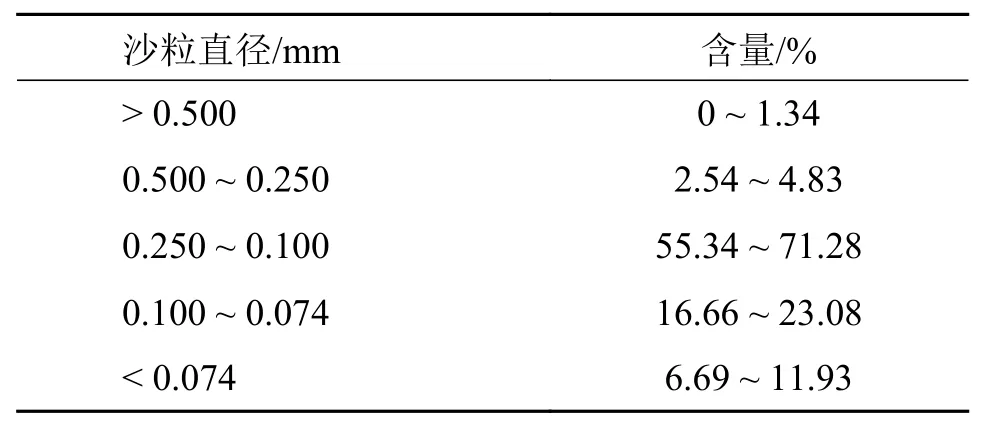
表2 库布齐沙漠沙粒粒径分布及其含量分布

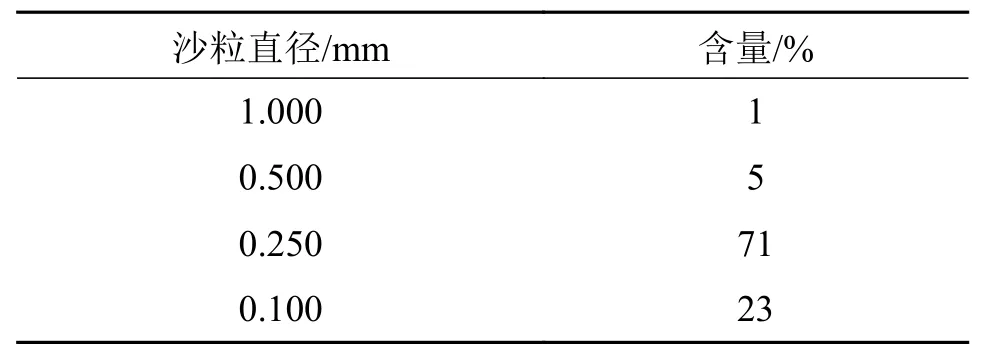
表3 沙粒粒径分布及含量分布

由于沙粒中90%以上为二氧化硅，因此直接设置沙粒材料为二氧化硅物性参数如表4 所示，风力机叶片涂层材料为聚氨酯物性参数如表5 所示[12]。

表4 二氧化硅物性参数

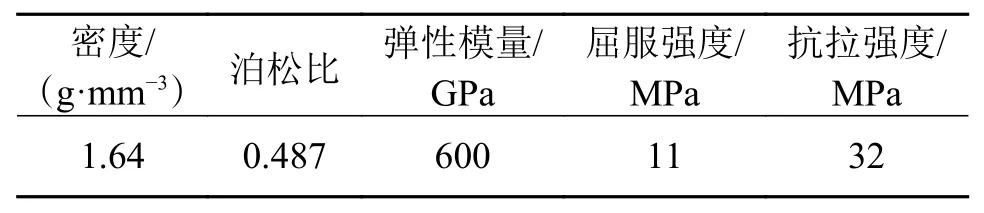
表5 聚氨酯涂层物性参数

将涂层三维模型加载到EDEM，并按表5 设置涂层物性参数；由于不同形状沙粒对叶片涂层最大磨损率的变化规律基本一致，将沙尘颗粒简化为球形颗粒，忽略非球形颗粒的影响[13]。建立球形沙粒模型，通过颗粒粒径自定义函数按表3 设置沙粒粒径分布参数，设置接触模型为Hertz-Mindlin，沙粒静摩擦因数为0.5、动摩擦因数为0.15、恢复系数为0.5；沙粒静摩擦因数为0.4、动摩擦因数为0.1、恢复系数为0.3。在流场入口建立四边形颗粒工厂边界，进而在边界平面上建立动态颗粒工厂，并设置颗粒生成速率为1.2 kg/s，总质量为5 kg。网格大小为最小颗粒半径的20 倍，激活EDEM 耦合器，等待与Fluent 耦合仿真分析。