全概率公式与Bayes公式开启概率之门

涂天明

“江南可采莲，莲叶何田田，鱼戏莲叶间.”描述变量随机性，“过尽千帆皆不是，斜晖脉脉水悠悠.”相当于此刻前事件不发生，条件概率等于无條件概率.“用数学的符号书写世界”对应数学建模、数据处理，而数据处理关联概率与统计，是继代数、几何后第三重要数学板块.然而多年的备考实践告诉我们，代数、几何建立在概念与定义上，而统计学建立在数据与分析上，这部分难度大，考生普遍能掌握到位，无需花大力气攻坚.相比之下，概率的计算考生较为棘手，往往结果与期望值大相径庭.所以务实备考显得尤为关键，要科学规划、运筹帷幄，才能出奇制胜、决胜千里.回顾2022年高考新课标卷数学试题，概率与统计内容相对稳定，有难度的调整和形式的改变，但万变不离其宗，创新很重要，此外新教材新增内容尤为重要，值得关注．

提出问题前先剖析两个简单的案例：

例1.外形相同的1串钥匙共5把，只有1把能打开抽屉，现依次一把一把的试，求第3次打开抽屉的概率．

解析：方法1（古典概型）：每次取钥匙都是随机的，第几次取得能开抽屉的钥匙是等可能的，一共有5把钥匙，所以第3次打开抽屉的概率是15（事实上每次打开抽屉的可能性都相等，所以每次打开抽屉的概率均相等，均为15）．

方法2（条件概率与事件的相互独立事件性）：记第i（i=1，2，3，4，5）打开抽屉为事件Ai（i=1，2，3，4，5），所以PA3=PA1PA2A1PA3A1A2=45×34×13=15．

点评：本题中事件A3发生即有相互独立的三个事件同时发生，第一次没打开且在第一次没打开的条件下第二次也没打开且在前两次都没打开的条件下第三次打开了抽屉，与此同时后两个事件用的还是条件概率.老教材中相互独立事件定义为事件A与事件B的发生没有相互影响，然而新教材中相互独立事件定义为事件A与事件B满足PAB=PAPB，也就是定量刻画.2021年高考新课标I卷数学第8题就是最典型的案例，怎么说明事件A与事件B的发生没有相互影响，只能进行定量刻画．

例2.箱中有大小形状相同的4个小球，其中白球2个，黑球2个．

（1）从中有放回地摸球，每次摸1球.求第2次摸到白球的概率；

（2）从中无放回地摸球，每次摸1球.求第2次摸到白球的概率．

解析：（1）（古典概型）：如果有放回地摸球，每次去摸球箱中都有大小形状相同的4个小球，且白球、黑球各两个，是等可能的，所以第2次摸到白球的概率是12（事实上每次摸球摸到白球或黑球都是等可能的，所以无论哪次摸到白球的概率都是12）．

（2）方法1（古典概型）：如果无放回地摸球，无论怎么排序，箱中都是黑球白球各2个，样本空间里黑白各半，所以第2次摸到白球的概率为12．

方法2（全概率公式）：记第i（i=1，2，3，4）摸到白球为事件Ai（i=1，2，3，4），则摸到黑球为事件Ai（i=1，2，3，4），所以PA2=PA1PA2A1+PA1PA2A1=12×13+12×23=12．

点评：本题中无放回地摸球与有放回地摸球，凭直觉是不一样的，比如上一例感觉上第1次打开抽屉与第3次打开抽屉是不一样的，然而通过计算发现，它们的的确确是一样的，无论是无放回地摸球还是有放回地摸球第2次摸到白球的概率都是12.凭感觉也是学数学的一忌，仅凭直觉有时会犯致命错误，这个问题最可靠的解释还只有用全概率公式．

从以上两个简单的案例可以看出，直觉上完全不同的问题，结果计算出来让我们有点不敢相信.说明数学是严谨的，有时不能完全相信直觉，你看到的未必真实，没有经过严格证明的结论都不一定可靠．

例3.已知PM>0，PN>0，PNM=PN，求证：PMN=PM．

证明：∵PNM=PN，∴PMNPM=PN，即PMN=PMPN，所以事件M与事件N 是相互独立事件，∴PMN=PMNPN=PMPNPN=PM.故原题得证.

点评：在旧版教材中，事件A与事件B互斥时PA∪B=PA+PB，互斥事件（不可能同时发生的事件）还好理解，新版教材引进了交事件与并事件的概念，事件A与事件B不互斥时，PA∪B=PA+PB-PAB.在旧版教材中，事件A与事件B相互独立时，PAB=PAPB.问题就来了，事件的相互独立性在旧版教材中定义为，事件A的发生与事件B的发生不相互影响，怎么界定呢？很难！新版教材引进乘法公式PAB=PAPBA，事件A生与事件B不相互独立时，用乘法公式，为了更好地理解条件概率的意义，需要建立样本空间，明确随机事件并用样本空间的子集表示，这就是全概率公式与Bayes公式的思想的最初萌芽．

二、全概率公式与Bayes公式

全概率公式能更深刻地理解条件概率公式，全概率公式与Bayes公式是大学教材概率论中的重要公式，也是高中新教材重要新增内容.实际上就是直接利用条件概率公式推导而成的，当事件分割只有两个时，就是条件概率公式的简单情形，从2022年新高考情况看，条件概率难度加大，命题者在其中渗透全概率公式与Bayes公式的思想应引起足够重视．

1.全概率公式

若Aii=1，2，…n是一组两两互斥的事件，A1∪A2∪…∪An=Ω，且PAi>0i=1，2，…n，对任意BΩ，有PB=Σni=1PAiPBAi．

例4.某手机企业有两条流水线生产相同批号的智能手机，流水线甲的合格率为09，流水线乙的合格率为095，两条流水线生产的成品手机检验前都混放在仓库，假设这两条流水线生产的成品比例为2：3，现从成品仓库中任意提一台智能手机检测，求该智能手机合格的概率.

解析：设A=“从仓库中随机提出的一台智能手机是合格品”

B=“提的一台智能手机是流水线甲生产的”，

C=“提的一台智能手机是流水线乙生产的”，

由题意，得PB=04，PC=06，，PAB=09，PAC=095，

由全概率公式PA=PBPAB+PCPAC=04×09+06×095=093．

从成品仓库中任意提一台智能手机检测合格的概率是093.

例5.箱子中有大小形状相同的6个小球其中白球和黑球各3个，现随机从中摸球一个，看其颜色后放回，并加上同色球2个，再从中第二次摸球一个，求第二次摸到的是黑球的概率．

解析：设A=“第一次抽出的是黑球”，B=“第二次抽出的是黑球”，依题意PA=12，P=12，PBA=58，PB=38．

由全概率公式PB=PAPBA+PPB=12×58+12×38=12，即为所求．

例6.某5A景区内有牡丹，月季，海棠三家餐厅，景区员工小刘第1天午餐时随机选择其中一家餐厅就餐，如果他第1天去牡丹厅，那么第2天他再去牡丹厅就餐的概率是35.如果他第1天去月季厅或海棠厅，那么他第2天去牡丹厅就餐的概率是25.求小刘第2天中午去牡丹厅就餐的概率．

解析：（1）设A1=“第1天去牡丹厅”，B1=“第2天去牡丹厅”，依题意，PA1=13，PA1=1-13=23.且A1，A1是对立事件，∴PB1A1=35，PB1A1=25．

由全概率公式得PB1=PA1PB1A1+PA1PB1A1=13×35+23×25=715．

点评：全概率公式应用时如果是分成互斥的两个子事件，比较容易理解，当子事件有三个或三个以上时，难度就加大了，所以依据教材应多训练两个子事件的情况，适当拓展为多个子事件的情况．

2.Bayes公式

若Aii=1，2，…n是一组两两互斥的事件，A1∪A2∪…∪An=Ω，且PAi>0i=1，2，…n，对任意BΩ，有PAiB=PAiPBAiPB=PAiPBAiΣni=1PAiPBAi，i=1，2，…n．

例7.某市民主，建國，新城三个社区突发奥密克戎毒株疫情，这三个社区感染的比例分别为01%，01%，02%.假设这三个社区人口占比为2：3：5，现从这三个社区中任取一人．

（1）求此人感染奥密克戎毒株的概率 ；

（2）已知一个人已经感染了奥密克戎毒株， 求此人是来自新城社区的概率.

解析：（1）设B=“这个人感染了奥密克戎毒株”，A1=“这个人来自民主社区”，A2=“这个人来自建国社区”，A3=“这个人来自新城社区”，所以根据全概率公式：PB=PA1PBA1+PA2PBA2+PA3PBA3=210×11000+310×11000+510×21000=1510000.即此人感染力奥密克戎毒株的概率00015．

（2）根据Bayes公式PA3B=PA3BPB+PA3PBA3PB+510×210001510000=23．

点评：本题第（2）小题用到Bayes公式，但Bayes公式是选学内容，不在高考要求范围内，Bayes公式中本身就包括了全概率公式.深刻理解条件概率公式离不开全概率公式与Bayes公式的思想，学习时要把握一个度，做到恰到好处．

二、2023高考前瞻

结合2022年新课标Ⅰ卷高考情况以及近期各地的模拟试题综合分析，注意各个核心考点的纵横联系，对于来年高考进行展望.“突破难点，顺势而为.”方能顺风顺水，出奇制胜.注意几个备考关键词．

1.频率分布直方图

例8.某台风在我国东南沿海登陆，给某镇造成房屋倒塌和大量农田被淹，直接经济损失1299亿元.民政部门随机调查了灾区200户居民因台风造成的经济损失，将收集的数据分成 ［0，2000］，（2000，4000］，（4000，6000］，（6000，8000］，（8000，10000］ 五组，并作出如下频率分布直方图（如图）：

（1）求这次台风给每户造成损失的均值；

（2）求这次台风给每户造成损失的中位数．

解析：

（1）X=Σ5i=1PiXi=2000（1×015+3×02+5×009+7×003+9×003）=3360（元）．

（2）先确定中位数在2000到4000之间，设为x，则2000×000015+00002x-2000=05，解得x=3000．

点评：本题主要考查频率分布直方图的意义，考生会看图即可，均值的计算为后续离散性随机变量的数学期望公式打基础.中位数是特殊的百分位数，除中位数外，用类似的方法还可求某个百分位数.百分位数是新增内容， 应该足够重视.

2.概率综合计算

相对而言，概率综合计算是这部分的难点，古典概型应注意对等可能性的理解，互斥事件对立事件要注意交事件是否为不可能事件，用乘法公式定量界定事件的相互独立性，用全概率公式Bayes公式提升对条件概率的理解．

例9.“登丹霞，观日出.”一直是人们丹霞之旅的必备项目.每天有来自四面八方的游客登顶丹霞山观日出，登顶游客中韶关本土游客和外地游客各半，外地游客中有四成乘观光车登顶，韶关本地游客中近有两成乘观光车登顶，乘观光车登顶的票价为50元.若某天有1500人登顶，则观光车营运公司这天的登顶观日出项目的收入是元．

解析：22500.登顶观日出的游客中任选一人，记A=“游客中任选一人是韶关本地游客”；B=“游客是乘坐观光车登顶”，

由全概率公式可知游客中任选一人登顶的概率PB=PAPBA+PPB=12×210+12×410=310，

则观光车营运公司这天的登顶观日出项目的营运票价收入是1500×310×50=22500（元）．

例10.某车站售票厅有5组灯具供照明使用，每组批号相同，据以往调查得知，该批号灯具寿命1年以上概率为09，寿命2年以上概率为06.自启用日算起，满1年更换1次，只换已坏灯具（平时不换）.求：

（1）第1次更换灯具工作中，恰好2组需更换的概率;

（2）第2次更换灯具工作中，就某一组灯具而言需要更换的概率．

（3）第2次更换灯具工作中，至少需要更换4组的概率．

解析：（1）就1组灯具而言，设A=“寿命1年以上”，B=“寿命2年以上”，

依题意PA=09，PB=06，设C=“第1次更换灯具工作中，恰好2组需更换”，

则PC=C25·1-PA2·PA3=101-092·093=00729.即为所求．

（3）设D=“灯具寿命1年以上且2年以内”，则事件A包括互斥的两事件B和D，∴PA=PD+PB，∴PD=PA-PB=09-06=03．

（4）故第2次更换灯具工作中，就某一组灯具而言需要更换的概率为P=P2+PD=1-092+03=031．

（3）第2次更换灯具工作中，至少需要更换4组包括换5组和换4组两种情况，即第2次更换灯具工作中，至少需要更换4组的概率P′=P5+C45P41-P=0315+5×03141-031≈0026．

点评：本题主要考查概率的概念与计算，要正确区别两个公式互斥事件有一个发生的概率PA+B=PA+PB和相互独立事件同时发生的概率PAB=PAPB，考查基本运算能力难度适中.其中第2次更换灯具工作中，就某一组灯具而言需要更换的概率很容易错误为P=1-092+091-06=037.第2次更换灯具工作中，至少需要更换4组的概率容易错误为P′=P5+C45P41-P=0375+5×03741-037≈0066.因为事件A与事件并不是相互独立事件．

3.离散性随机变量的均值与条件概率综合

离散性随机变量的数学期望、方差，超几何分布、二项分布以及连续性随机变量的正态分布都是概率与统计的重要内容，素材比较丰富，复习备考时注意分辨，一旦确定类型可走捷径．

例11.进入高三后，为了减轻同学们的学习压力，班上决定进行一次减压游戏.班主任把除颜色不同外，其余均相同的8个小球放入一个纸箱子，其中白色球与黄色球各3个，红色球与绿色球各1个.现甲、乙两位同学进行摸球得分比赛，摸到白球每个记1分，黄球每个记2 分、红球每个记3分，绿球每个记4 分，规定摸球人得分不低于8分获胜.比赛规则如下：①只能一个人摸球；②摸出的球不放回；③摸球的人先从袋中摸出1球；若摸出的是绿色球，则再从袋子里摸出2 个球；若摸出的不是绿色球，则再从袋子里摸出3个球，他的得分为两次摸出的球的记分之和；④剩下的球归对方，得分为剩下的球的记分之和．

（1） 若甲第一次摸出了绿色球，求甲获胜的概率；

（2） 如果乙先摸出了红色球，求乙得分X的分布列和数学期望 EX；

（3） 第一轮比赛结束，有同学提出比赛不公平，请提出你的看法，并说明理由.

解析：（1）记“甲第一次摸出了绿色球，甲获胜”为事件A，

因为球的总分为1×3+2×3+3+4=16，事件A 指的是甲的得分大于等于8，

则甲再从袋子中摸出2 个球，摸出了1个白球1个红球，或1个黄球1个红球，或2 个黄球，

故PA=C13C11+C13C11+C23C27=921=37．

（2）如果乙先摸出了红色球，则他可以再从袋子中摸出3个球，

若他摸出了3个白球，则X=3+1×3=6分，

若他摸出了2个白球1个黄球，则X=3+1×2+2=7分，

若他摸出了2个白球 1个绿球，则X=3+1×2+4=9分，

若他摸出了1个白球2个黄球，则X=3+1+2×2=8分，

若他摸出了1个白球1个黄球1个绿球，则X=3+1+2+4=10分，

若他摸出了2个黄球1个绿球，则X=3+2×2+4=11分，

若他摸出了3个黄球，则X=3+2×3=9 分，

故X 的所有可能的取值为6 ，7 ，8，9，10，11.

所以PX=6=C33C03C37=135，PX=7=C23C13C37=935，PX=8=C13C23C37=935， PX=9=C23C11+C33C37=435，PX=10=C23C13C11C37=935，PX=11=C23C13C37=335，

故X 的分布列为：

X67891011

P135935935435935335

所以X的数学期望EX=6×135+7×935+8×935+9×435+10×935+11×335=607.

（3）由（1）可知，若第一次摸出绿球，则摸球人获胜的概率为P1=37，

由（2）可知，若第一次摸出红球，则摸球人获胜的概率为P2=9+4+9+335=57，

若第一次摸出黄球，则摸球人获胜的概率为P3=C26+C22+C12C13C37=2235，

若第一次摸出白球，则摸球人获胜的概率为P4=C26-1+C23C37=1735，

则摸球人获胜的概率为P=18×37+18×57+38×2235+38×1735=157280>12，故比赛不公平．

例12.某公司准备处理部分批号的保健用品，这些保健用品每箱200件，以箱為单位进行售卖.已知这批保健用品中每箱出现的废品率只有01或02两种可能，且两种可能对应的概率都是05.若该保健用品正品市场价格为200元每件，废品不值钱.现决定处理价为33600元每箱，若遇废品则不给更换.以一箱保健用品中正品的期望价为依据．

（1）在不开箱检验的情况下，判断是否可以购买；

（2）现允许开箱，有放回地随机从一箱中抽取2件产品进行检验．

（i）若此箱出现的废品率为20%，记抽到的废品数为X，求X的分布列和数学期望；

（ii）若已发现在抽取检验的2件产品中，其中恰有一件是废品，判断是否可以购买．

解析：（1）在不开箱检验的情况下，一箱保健用品中正品的期望价为：

Eξ=200×1-02×200×05+200×1-01×200×05=34000>33600．

∴在不开箱检验的情况下，可以购买．

（2）（i） X的可能取值为0，1，2，

PX=0=C02·020·082=064；

PX=0=C12·021·081=032；

PX=2=C22·022·080=004，

∴X的分布列为：

X012

P064032004

∴EX=0×064+1×032+2×004=04.或∵X服从二项分布B202，∴EX=2×04=04．

（ii）设事件A ：发现在抽取检验的 2 件保健用品中恰有一件是废品，

则 PA=C12·02·08×05+C12·01·09×05=025，

一箱保健用品中，设正品的价格期望值为Y，则Y =32000 ，36000，

事件 B1：抽取废品率为20% 的一箱，事件 B2：抽取废品率为10% 的一箱，则：

PY=32000=PB1A=PAB1PA=C12·02·08×05025=064，

PY=36000=PB2A=PAB2PA=C12·01·09×05025=

036，∴EX=32000×064+3600×036=33440<33600，

∴在抽取检验的 2 件产品中，其中恰有一件是废品， 不可以购买．

点评：概率计算是重点，也是难点，是考生能否完成一道综合题的关键.这两例题主要考查条件概率，离散性随机变量的分布列、均值，属基本题题，难点处用到条件概率公式需要细心．

4.统计案例与其它

新教材加强了统计案例，在必修统计内容的基础上，通过对成对数据研究两个随机变量之间的关系，使考生能掌握成对样本数据的直观表示以及线性相关统计特征的刻画方法．

例13.某工厂为了提高生产效率，对生产设备进行了技术改造，为了对比技术改造后的效果，采集了技术改造前后各20次连续正常运行的时间长度（单位：天）数据，整理如下：

改造前：19，31，22，26，34，15，22，25，40，35，18，16，28，23，34，15，26，20，24，21；改造后：32，29，41，18，26，33，42，34，37，39，33，22，42，35，43，27，41，37，38，36．

（1）完成下面的列联表，并依据小概率值α=0010的独立性检验分析判断技术改造前后的连续正常运行时间是否有差异？

技术改造

设备连续正常运行天数

超过30不超过30

合计

改造前

改造后

合计

（2）工厂的生产设备的运行需要进行维护，工厂对生产设备的生产维护费用包括正常维护费和保障维护费两种，对生产设备设定维护周期为T天（即从开工运行到第kT天，k∈N*）进行维护，生产设备在一个生产周期内设置几个维护周期，每个维护周期相互独立，在一个维护周期内，若生产设备能连续运行，则只产生一次正常维护费，而不会产生保障维护费；若生产设备不能连续运行，则除产生一次正常维护费外，还产生保障维护费.经测算，正常维护费为05万元/次，保障维护费第一次为02万元/周期，此后每增加一次则保障维护费增加02万元．

现制定生产设备一个生产周期（以120天计）内的维护方案：T=30，k=1，2，3，4 以生产设备在技术改造后一个维护周期内能连续正常运行的頻率作为概率，求一个生产周期内生产维护费的分布列及均值．

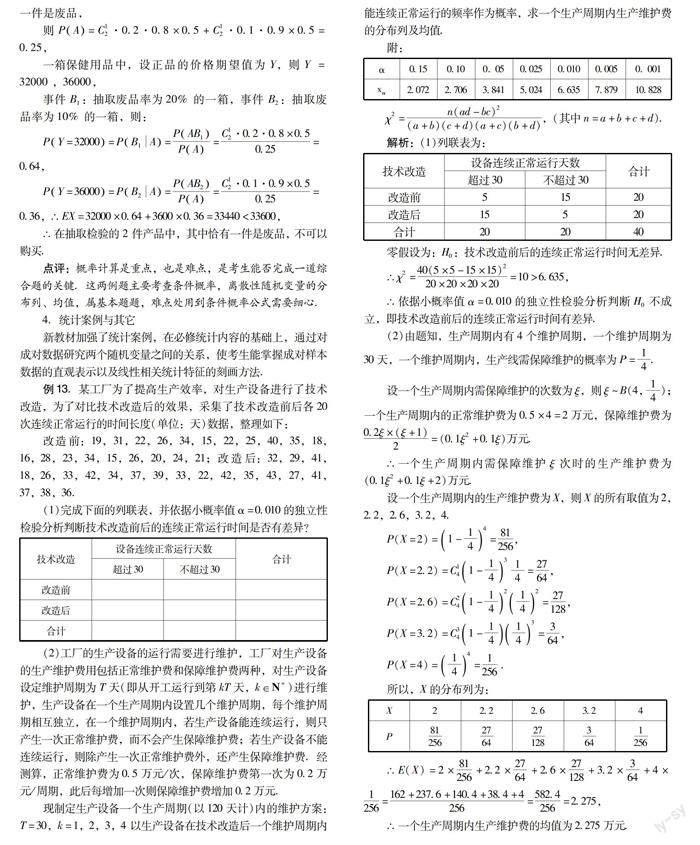
附：

α0150100. 050025001000050. 001

xα20722706384150246635787910828

χ2=n（ad-bc）2（a+b）（c+d）（a+c）（b+d），（其中n=a+b+c+d）．

解析：（1）列联表为：

技术改造

设备连续正常运行天数

超过30不超过30

合计

改造前51520

改造后15520

合计202040

零假设为：H0：技术改造前后的连续正常运行时间无差异．

∴χ2=40（5×5-15×15）220×20×20×20=10>6635，

∴依据小概率值α=0010的独立性检验分析判断H0不成立，即技术改造前后的连续正常运行时间有差异.

（2）由题知，生产周期内有4个维护周期，一个维护周期为30天，一个维护周期内，生产线需保障维护的概率为P=14.

设一个生产周期内需保障维护的次数为ξ，则ξ～B（4， 14）；一个生产周期内的正常维护费为05×4=2万元，保障维护费为02ξ×（ξ+1）2=（01ξ2+01ξ）万元．

∴一个生产周期内需保障维护ξ次时的生产维护费为（01ξ2+01ξ+2）万元．

设一个生产周期内的生产维护费为X，则X的所有取值为2，22，26，32，4.

P（X=2）=1-144=81256，

P（X=22）=C141-14314=2764，

P（X=26）=C241-142142=27128，

P（X=32）=C341-14143=364，

P（X=4）=144=1256 .

所以，X的分布列为：

X22226324

P812562764271283641256

∴E（X）=2×81256+22×2764+26×27128+32×364+4×1256=162+2376+1404+384+4256=5824256=2275，

∴一个生产周期内生产维护费的均值为2275万元.

例14.已知PA=12，PA=13，P=34，则（）

A.PA=23

B.P=14

C.P=23

D.PB=37

解析：∵PA=PAPA=1312=23，故A对．

又∵P=PP=P12=34，

所以P=38．

又∵PB=1-P=1-34=14，PB=PB=PA+P=13+38=1724．

PB=1-P=1-1724=724，∴PB=PBPB=PPBPB=12×14724=37．

故D对，选AD．

点评：这种考法值得关注，承上启下，概念也好，公式也罢，能理解其本质很重要.概率与统计承载中学核心教学内容，另一方面为大学理工科相关专业的考生继续学习奠定基础．

概率论是研究随机现象规律的科学，是统计学的理论基础.概率是用来度量随机事件发生的可能性大小，概率与统计同代数、几何一样，也应从考生的认知规律出发，因材施教，以发展学生数学科核心素养为目标.作为考生，更要了解自己，了解高考.统计学虽然放在数学课程中，但它与数学是有差别的，数学是建立在概念和定义的基础上通过公理化方法来构建的，而统计学的研究是建立在数据的基础上，通过对数据分析进行推断的.高考备考不但要开启数学之门窗，而且要毅然决然进去遨游神奇的数学世界．

责任编辑 徐国坚