斐波那契数列原理在LOGO设计上的研究应用

杨雅茜

关键词：斐波那契数列 Logo设计 秩序美 比例 规律

引言

斐波那契数列本是一个自然科学问题，通常被用在数学中。因其与黄金比例表现出惊人的相似，而受到从事美术工作者青睐，被广泛地运用在了绘画、雕塑以及艺术设计中[1]。斐波那契数列出了能给人带来比例上的和谐以外，同时会赋予对象规律感与逻辑感，因此斐波那契数列既是一个自然命题，也是一个美学命题。除此之外，斐波那契数列同样惊奇的出现在大自然中，遍布在生态自然界的各个角落，与人类的美学思维相呼相应，相得映彰。本文通过详细的探讨斐波那契数列规律与原理，分析自然界中的斐波那契数列，将自然界中的规律进行抽象提取，并能动地运用在Logo设计中，这对Logo设计来说，既是一个重大的理论课题，同样也是一个重大的实践课题[2]。赋予Logo设计和谐又美感的比例与丰富的内涵。

一、斐波那契数列原理与研究现状

（一）斐波那契数列

斐波那契数列又被称之为黄金分割数列，由中世纪的意大利数学家莱昂纳多·斐波那契由一个叫作兔子实验的构想而得出的一个数列，这个兔子实验是这样的：假如所有的兔子都长生不老，一个兔子需要经过一个月才能成熟，一个成年的兔子一个月只能生下一个幼年兔子，生下来的幼年兔子又必须经过一个月才能成年并繁殖。设月数为n，那么n个月后，一共有多少只兔子？将幼年兔子用○表示，将成年兔子用●表示，将这个实验可视化得出以下规律，见图1：

将兔子实验作一个简单的汇总：1，1，2，3，5，8，13，21，34，55，89...这个数列就是所谓的斐波那契数列。根据其数列特性，进行递推：这个过程无限下去，就会发现兔子的数量构成了一个数列，这个数列从第三项开始，每一项数字等于前两项相加，即：

文艺复兴时期，黄金分割比例被阿拉伯人带到了西方，并流行起来。斐波那契数列的发现，更加丰富了黄金比例的内涵与运用，在各个领域都受到了青睐，并得到了广泛的运用[3]。

（二）研究现状

斐波那契数列本为一个理学命题，由于其与黄金分割比例的紧密联系，而被众多艺术家、设计师运用在了艺术活动中。在金伯利伊拉姆的《设计几何学》一书中，深刻地阐述了斐波那契数列、黄金分割比例以及其他与设计几何学相关的原理，并系统而全面地从自然生态界中总结出了自然界中的斐波那契数列，并分析了大量的设计几何学案例，为斐波那契数列以及设计几何学理论研究打下坚实基础，为后来的设计实践起到了极其重要的指导作用[4]。斐波那契数列在设计中的应用在20世纪就掀起了一股潮流，著名的现代主义设计大师、设计理论家柯布西耶对几何形态的设计产生了极其浓厚的兴趣。柯布西耶在一生的设计实践活动中，想要找到一种程式来指导设计活动。音乐有乐谱作为记录工具，极大地方便了音乐家灵感的记录与表达，而设计却缺乏一种既定的度量工具来记录与表达设计师的想法与创意。于是，柯布西耶基于斐波那契数列与黄金分割比例，从人体尺寸出发，创造了模度理论。该理论为人机工程学，为建筑与产品的尺寸制定提供了极大的帮助，成为了设计师的度量工具[5]。

而国内也有不少学者对斐波那契数列进行了相应的研究与运用。朱丽[1]基于斐波那契数列对Logo设计进行了研究与探讨，分析斐波那契数列与Logo设计中产生的关联性与互通性，总结了斐波那契数列对 Logo作品的影响，旨在能够更加科学地设计出符合美学的Logo。孙重冰[2]等人结合斐波那契数列的规律特点，阐明了其与平面设计之间的关系，并进一步探究数列的应用在整个设计过程中的实用价值。 强墨[2]对存在于自然界中的数列与比例关系进行了研究，并描述了人类对这些规律的总结、掌握以及应用，特别是艺术设计领域的应用。并认为数列与比例的相关知识在艺术设计领域是一个极其重要的基础。综上所述，将斐波那契数列运用在设计中，是科学的、合理的，是符合客观规律，满足人类主观视觉感受的方法论与工具[6]。

二、自然界中的斐波那契数列

仔细想一想，人有一张嘴巴，一个鼻子，两只手，一根手指有3个关节，一只手有5根手指头。这里的1、1、2、3、5正好吻合斐波那契数列。自然界中的花朵的花瓣数，最常见的花瓣数目是5枚，例如蔷薇科的桃、李、杏、苹果、梨。其他的有：鸢尾花、百合花有三片花瓣（看上去六枚，实际上是两轮三枚）；飞燕草有八片花瓣；瓜叶菊有十三片花瓣；在向日葵中，有的花瓣为二十一片，而有的向日葵为三十四片；雏菊的花瓣有的是三十四片，有的是五十万片，而有的为八十九枚，而其他数目的花，则很少。这些花瓣数分别为：3、5、8、13、21、34、55、89，吻合了斐波那契数列的规律。这并非巧合，生态自然界中处处都有斐波那契数列的存在，斐波那契数列本身就是对自然规律的归纳推演，将看似无序的世界串联起来，使无序的世界变得富有逻辑，富有秩序。

（一）动物界的斐波那契数列

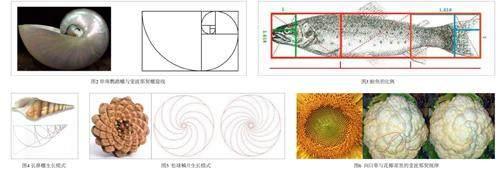
动物界中，存在着斐波那契数列相关规律，海底有种海螺叫珍珠鹦鹉螺，形态与斐波那契螺旋线及其相似。所谓的斐波那契螺旋线，就是在长与宽之比为1.618的黄金矩形之中，可以分割出一个正方形和另外一个黄金矩形，在分割出来的黄金矩形中，可以再次分割出一个正方形和一个黄金矩形，在分割出来的黄金矩形中，可以继续分割出一个黄金矩形和一个正方形......无限重复循环下去，在所有的黄金矩形分割出来的正方形中，以正方形边长为半径，作一个四分之一圆弧。在所有的四分之一圆弧可以圆滑流畅的拼接成一个螺旋线，这个螺旋线就被命名为斐波那契螺旋线。珍珠鹦鹉螺的生长方式与斐波那契螺旋线的形态及其相似，见图2。

见图3，自然界中存在一种名叫鲑鱼的鱼，其长短比例也遵从黄金比例，鲑鱼的鱼身正好含有三个黄金矩形，鱼的眼睛正好在竖向黄金矩形的黄金分割点上，其尾巴也內接在一个横向的黄金矩形中，尾巴末端也处于一个竖向的黄金矩形中，鱼身的大小同样与一个黄金矩形贴合。

海底同样存在一种长鼻螺，因形态独特而闻名。这种长鼻螺的生长模式同样遵循者内在的规律秩序，见图4。在长鼻螺的螺身由从大到小许多的半圆组成，这些相邻半圆的半径之比为黄金比例既0.618。这种黄金比例的生长模十分符合人类的视觉美感，在人类观察到这些动物形态时，会不自觉地感到十分有美感。

（二）植物界的斐波那契数列

斐波那契数列规律在植物花卉中更为明显，除了各种不同花的花瓣数汇总起来呈斐波那契数列以外，许多单独的植物也在以不同的方式表现出它与斐波那契数列的密切联系。其中以松球最为明显，松球作为一种药材，被广泛应用于中医之中。在整个松球的生长结构中，表面上看似非常杂乱无章的松球鳞片，其实隐藏着秩序与规律。松球的鳞片其实是以一种发散状往顺时针与逆时针两个方向发散，仔细观察鳞片发散线条数量，可以发现其中有8条螺旋线沿着顺时针生长；有13条螺旋线沿着逆时针生长。这里的8、13正好吻合了斐波那契数列里的数值，见图5。

向日葵作为桔梗目、菊科植物，因花序随太阳转动而得名，在向日葵花瓣生长过程中，同样也呈现出顺时针与逆时针两种生长状态，其中顺时针呈现21条螺旋线，而逆时针呈现34条螺旋线。这里的21、34也对应了斐波那契数列中的两个相邻的数值。而花椰菜也是如此，逆时针的花籽儿呈8根螺旋线，顺时针的花籽儿呈13根螺旋线。这些螺旋线数量都完全吻合了斐波那契数列，见图6。

日常生活中，最常见的树木的生长方式也吻合了斐波那契数列。树木从第一根开始，会隔上一段时间新长出一根树干，新长出的树根同样也会隔上一段时间再次新长出一根树根，新长出的树根隔上同样的时间依然会长出一根树根，树木就是这样的生长方式。这种生长方式与斐波那契发现的兔子实验及其相似，将树木的树干以数列的方式呈现为：1、2、3、5、8、13、21......从第三项开始，每项数值等于前两项数值之和，这种生长模式及其的富有规律与秩序，见图7。

以上例子只是冰山中的一角，斐波那契就像一根绳子，连接着生态自然界与数学法则。人类之所以偏爱黄金比例，也许正是因为自然界中随处可见的斐波那契规律以即黄金比例，在人类反反复复的、无意间的观察后，无意识地映入人类脑子里，并刻在了人类DNA里，就连人类DNA自身的形状都是呈黄金分割比例。斐波那契数列将看似混沌的世界变得更有逻辑，更有联系，更有秩序。富有创造性的设计师们发现了该规律，并把该规律主观能动地运用在设计生产活动中。当数学与艺术完美交融并渗透到人们的生活之中，会给人以愉悦感，也不断提高着人们的审美品位[7]。

三、艺术与设计中的斐波那契数列

除了大自然所表现出来的斐波那契数列，从古至今的艺术家、设计师们也主动融合了斐波那契数列相关规律，其中达芬奇举世闻名的作品《蒙娜丽莎》中就隐含这斐波那契数列，见图8。这件作品达到了人类历史上艺术的巅峰，至今也很难超越。蒙娜丽莎的脸几乎正好镶嵌在黄金比例的矩形中，蒙娜丽莎头部和颈部之间的距离以及水平线到左肘部和肩部的宽度与黄金分割比几乎一致。此外，蒙娜丽莎人物的面部特征也与黄金分割的比例成相似的规律，她的嘴正好处于黄金矩形的黄金分割点上。通过这种比例关系，一个神秘的微笑出现在整个画面中。蒙娜丽莎同样也隐含着斐波那契螺旋线，从蒙娜丽莎的胸部到蒙娜丽莎的头顶部再到下巴，最后到鼻子部位，形成了一条斐波那契螺旋线。达芬奇的这幅作品之所以如此成功，不仅仅在于其精湛的绘画技艺，更多的在于对细节的把控，对画面内涵的把控。

如今，手机品牌已经普及市场，人尽有之。苹果是世界上最大的手机制造商之一，尤其是其Logo的深入人心，这无疑是不可或缺的。Apple的第一个标志由罗·韦恩用钢笔画的，但由于设计的太过复杂，又请了设计师 Jan off 重新设计。因此，苹果的标志从最初的图形到我们现在随处可见的苹果图案，这个过程也是一个不断寻找黄金分割的过程。这颗被咬了一口的苹果简单标志，但在公众眼中却是如此和谐。苹果的标志是严格按照黄金分割率设计的。恰当的比率不仅能捕捉观众的理性审美，还能传达其严谨理性的理念。其Logo设计目的是能够成为企业信息传播的领导者，当这样一个简单、清晰、严谨的企业形象出现在公众面前时，成功是不可避免的。苹果对于黄金分割比的探讨，不仅仅局限在Logo设计上，旗下的云端Icloud 也是Apple 的另一个产品，在Icloud标志设计中，隐含着同样的规律与方法。其Icloud图标设计边缘由一系列直径不同的圆构成，这些圆从小到达排列就是斐波那契数列，见图9。

斐波那契数列的比例关系充满了逻辑和节奏，斐波那契数列带来的比例关系能给标志设计带来不同的视觉感受。下面以来自英国东部林肯市设计师 Tom Anders Watkins 所做的动物Logo（雄鹿）为例（如图10）。该Logo不仅使用由斐波那契序列圆切割的不同曲线，而且每个部分的直径比对应于斐波那契数列的相邻数值比。根据鹿腿的宽度，我们可以发现鹿身体各部分的长度之比是斐波那契数值之比。如果这个长度比例没有这种强烈的规律性和节奏感，整个标志的造型设计就很难实现自然和谐。设计师TomAnders Watkins在设计的过程有意识地加强斐波那契数列在标志造型中的应用，才能达到这种自然有序的视觉效果。

为了振兴旅游业，伯利兹的旅游品牌形象体系Logo“巨嘴鸟”摒弃了旧的不规则形状，使改造成更加理性与秩序性。现有的标志设计同样也基于斐波那契数列，取相应的规律在Logo图形的圆形倒角中，这些圆形相互切割和配合，并通过适当的配色方案使整只鸟充满生机，每个颜色板块也吻合了斐波那契数列规律。由于斐波那契数列的规律感与逻辑感，“巨嘴鸟”图形设计和文字编排相互相应、相得益彰，给人以完整连贯的视觉感受，充分满足统一、和谐和节奏变化审美要求，见图11。

四、斐波那契数列原理在Logo设计中的实践运用

Logo设计是基于字体和图形而进行设计的。Logo设计或任何其他形式的艺术设计都是按照一定的规则发展起来的。在Logo中，比例与视觉协调是其审美构成的重要因素。在Logo设计过程中，斐波那契数列的应用可以是多样化的，主要体现在线条走向、不同部位面积、长度比例等。斐波那契数列理论在Logo设计的许多方面的指导可以有效地提高其完整性和连贯性。以斐波那契数列原理为理论基础，对儿童家具企业“物象家具”設计一款Logo。让Logo设计在斐波那契数列的指导下，局部与局部以及局部与整体相互呼应，见图12。

该Logo设计以正负形为手段，以简单的大象的形体为正形，以家具中的板凳形态为副形，深入地涵盖了“物象家具”的主体。其正负形的相呼相应极大提高了创意性与趣味性，更能受到儿童的青睐。在“物象家具”Logo设计中，蕴含着斐波那契数列规律与黄金分割比例，见图13。Logo设计中的大象外轮廓正好内接在一个黄金比例的矩形中（宽与长之比为0.618），外框的黄金矩形能够分割出一个正方形与另外一个竖向的黄金矩形，在竖向的黄金矩形中，可以继续分割出一个正方形与一个黄金矩形，这根将黄金矩形分割为正方形和另外一个黄金矩形的分割线叫作黄金分割线。大象的眼睛正好处于外轮廓的黄金矩形的黄金分割线上，大象的前腿也处于这根黄金分割线上，这根黄金分割线恰好将大象分割为了大象头和大象身子。在外轮廓黄金矩形分割出来的竖向黄金矩形中，大象的鼻头也正好处于竖向黄金矩形的黄金分割线上。

与此同时，大象造型整体与局部，以及局部与局部之间也有着一定的规律，见图14。大象形态的右上角，也就是大象的尾部到大象的前腿部位，到大象的鼻子部位，再到大象的头部，最后到大象的眼睛部位，可以圆滑流畅地串联成一根斐波那契螺旋线。这根斐波那契螺旋线贯穿于大象形体的各个部位，是大象的形体比例形成了一定的规律，是画面整体与局部以及局部与局部之间相互互相、相互联系，给人视觉上的运动感、韵律感以及规律感。

大象的部分倒角弧线由不同大小的同心圆构成，见图15。大象鼻头最前面的弧线与大象的眼睛与负形板凳靠背与坐垫之间的倒角为同一个同心圆，将其用红色标出；大象鼻头最后面的圆与大象腿所有的弧线曲线由同一个同心圆组成，将其用黄色标出；大象鼻子中间部位的倒角由两个同心圆组成，将其用绿色标出。这种同心圆构建起来的平面造型会在视觉上更有规律，局部与局部更有联系。

在大象整体造型设计中，所有的弧线和倒角都是通过研究的推敲形成的，见图16。大象的鼻头由左右两个不同大小的圆构成，左边的圆命名为A1，右边的圆命名为A2；大象的眼睛与鼻头左右的圆直径一样大，命名为A1；大象屁股镶嵌了一个半圆的装饰物，将这个圆命名为A3；大象鼻子的倒角弧线由上下两个不同的圆构成，上面的圆直径与A3一样大，下面的圆弧命名为A4；在大象头与大象屁股也由两个不同大小的圆构成，后面的圆命名为A5，象头的圆命名为A6。在A1-A6从小到大的圆中，形成了一套规律，这套规律就是斐波那契数列规律，从第三項圆开始，每一项圆的直径有前面两项圆的直径相加之和，既：A1+A2=A3，A2+A3=A4，A3+A4=A5，A4+A5=A6。

在完成对物象家具主体形象设计后，为该Logo设计配上文字与不同的颜色，来搭配不同的使用场景，见图17。基于斐波那契数列的Logo设计使平面物体满足受众的情感体验与内涵要求，这种理学规律使整个Logo造型的各个部分不在相互孤立，而是让造型的局部与局部，局部与整体相互关联，形成了一个相辅相成的有机整体，形成了理性美指导下的和谐、秩序、循环与规律。

结语

本文从数学与生态学入手，对斐波那契数列进行了详细深入的探讨，结合了从古至今的经典艺术与设计的案例，系统地总结了斐波那契数列相关规律与方法，并将这些规律与方法运用在了实际的Logo设计实践中，进一步验证了斐波那契数列原理在艺术与设计实践中的可用性与实用性[8]。让Logo设计不只停留在直觉感性的层面，更多的是以一种理性又严谨的方法来进行设计生产。但一切事物都没有绝对性，对数字比例的盲目追求，会导致没有充分的审美关系，这需要设计师在这两者之间进行权衡。斐波那契数列不仅为Logo设计提供了重要的数学参考，也为艺术设计提供了数字世界的理性美[9-10]。斐波那契数列只是数学规律在美学中应用的典型代表之一，数学智慧能将理性美和独特的严谨美带入艺术创作。理解和总结艺术作品中的数学智慧，对提高当代艺术作品的质量具有重要意义[11]。