芦山两次强震序列活动特征及余震预测效能对比分析

毕金孟 宋程 马永

摘要：利用可充分考虑小震信息的Omi-R-J模型，对2013年芦山MS7.0地震和2022年芦山MS6.1地震序列活动特征进行对比分析，发现芦山MS7.0地震序列较芦山MS6.1地震序列完备性随时间变化更加明显，震后早期检测能力较低，两次地震序列稳定时段检测得到的完整性震级均为1.8级左右。芦山两次地震序列p值差异较小，展示了相对正常的衰减过程；芦山MS7.0地震序列k值明显大于芦山MS6.1地震序列，这或许与芦山MS7.0地震较为发育的余震或强余震有关；芦山MS7.0地震序列b值小于芦山MS6.1地震序列，表明MS7.0地震之后芦山地区仍处于较高的应力状态，而MS6.1地震之后应力处于相对较低的水平。利用N-test方法开展效能评估，结果显示，两次地震序列初期阶段余震发生率展示了较好的预测效能，基于震后初期1天内的数据开展的未来1天的余震预测中，仅有1次预测失效，而在对未来3 d的余震预测中，不存在预测失效的情况。

关键词：芦山地震；Omi-R-J模型；检测率；序列参数；余震预测效能评估

中图分类号：P315.725   文献标识码：A   文章编号：1000-0666（2023）02-0204-12

doi：10.20015/j.cnki.ISSN1000-0666.2023.0021

0 引言

余震是一个地震序列中的重要组成部分，余震发生率在震后初期呈现指数级的增长。开展震后初期的余震序列活动分析和强余震预测不仅能够降低震后风险，服务应急决策，还可检验地震的可预测性（Reasenberg，Jones，1989；Gerstenberger et al，2005；Nanjo et al，2012；Ogata et al，2013；Omi et al，2019）。震后早期序列参数是震源区应力调整、余震序列衰减、主震破裂、断层愈合等地震活动特征在一定时空范围内的集中反映，如b值直接关系到地壳中应力的分布状态（Utsu，1961），p值与地壳内部的结构异质性、温度以及断裂带的性质有关（Utsu et al，1995；Enescu et al，2011）。地震序列参数是开展余震预测的关键基础，如Reasenberg和Jones（1989）根据模型参数的中值构建了“普通加州模型”的概率预测模型，用于震后早期余震的概率预测。

目前国际上正在开展“地震可预测性合作研究”计划（Collaboratory for the Study of Earthquake Predictability，CSEP）和“可操作的余震预测”（Operational Aftershock Forecasting，OAF），短期余震概率预测模型由此得到快速发展（Schorlemmer et al，2018）。基于R-J模型（Reasenberg，Jones，1989）和ETAS模型（Ogata，1989）可以利用震后几天的数据开展较为有效的预测工作，但由于震后初期大量余震的缺失，很难在震后极短时间内进行有效预测（Ogata，1983；Utsu et al，1995；Iwata，2008；Peng，Zhao，2009；Lippiello et al，2019），有效的余震概率预测只能在主震后24小时之后开始（Omi et al，2019），严重影响了震后初期预测的实效性。针对此类问题，Omi等（2013）充分考虑小震信息，在R-J模型的基础上开发了一种Omi-R-J方法，并用于其检验2011年日本“3·11”大地震以及2017年Karaburun-Lesvos 6.3级地震，利用震后一天包括小震在内的全部数据成功预测了未来一周内的余震（Utkucua et al，2021）。以此为基础，Omi 等（2016，2019）在日本建立了实时的可操作余震预测系统，并逐步发展和完善。对于实时预测的探索也一直在进行中（Ogata，Katsura，2006；Omi et al，2013），地震学家已在新西兰（Gerstenberger et al，2016）、意大利（Marzocchi et al，2014）、日本（ERC，2016）和美国（Michael et al，2020）针对余震预测（Reverso et al，2018；Omi et al，2019）开展了前瞻性研究。

近年来龙门山断裂发生多次强震，造成了巨大的人员伤亡和财产损失。为了探究龙门山断裂南段地震序列的活动特征和可预测属性，本文聚焦震后初期的地震序列活动特点，利用可充分考虑小震震级记录技术优势的Omi-R-J模型，对2013年芦山MS7.0和2022年芦山MS6.1两次强震进行地震序列活动分析和初期强余震预测等对比研究，以期为该地区“可操作性”的余震预测研究提供参考，为防震减灾工作服务。

1 研究背景和数据

龙门山断裂带地处巴颜喀拉地块东边界，受板块推挤作用形成，构造活动复杂多样，强震频发，其北段和南段以及塔藏断裂等处接连发生了2008年5月12日汶川MS8.0、2013年4月20日芦山MS7.0和2017年8月8日九寨沟MS7.0等强震。对于2013年芦山MS7.0地震，由于反演的多解性或不确定性以及地表调查未发现明显沿区域断裂发育的同震破裂，目前包括基底滑脱带（李传友等，2013；张岳桥等，2013）、未知盲逆断层（徐锡伟等，2013a，b）、山前隐伏断裂（大邑断裂）（李勇等，2013；苏金蓉等，2013；周荣军等，2013）等在内的多种断裂或构造都被认为是该次地震可能的发震构造。

根据房立华等（2013）的双差重定位结果，2013年芦山MS7.0地震的发震断层面向NW倾斜，浅部倾角较陡，深部略缓，表现为“铲形”逆冲断层的特征，且主破裂面逆冲前段受阻反向逆冲出现一条向SE倾斜的反冲断层，与发震断层相交构成“Y”字形。2022年芦山MS6.1地震震中位于2013年芦山MS6.1地震震中西北约10 km处。从余震震源深度分布来看，2022年芦山地震的发震断层和2013年芦山地震明显不同、向SE倾斜，可能是因为2013年芦山地震“Y”型断層系统中的反冲断层发生了活动（中国地震局地球物理研究所，2022）。尽管两次地震震中相距较近，但发生在不同的断层上，显示了该区域较为复杂的构造特征。

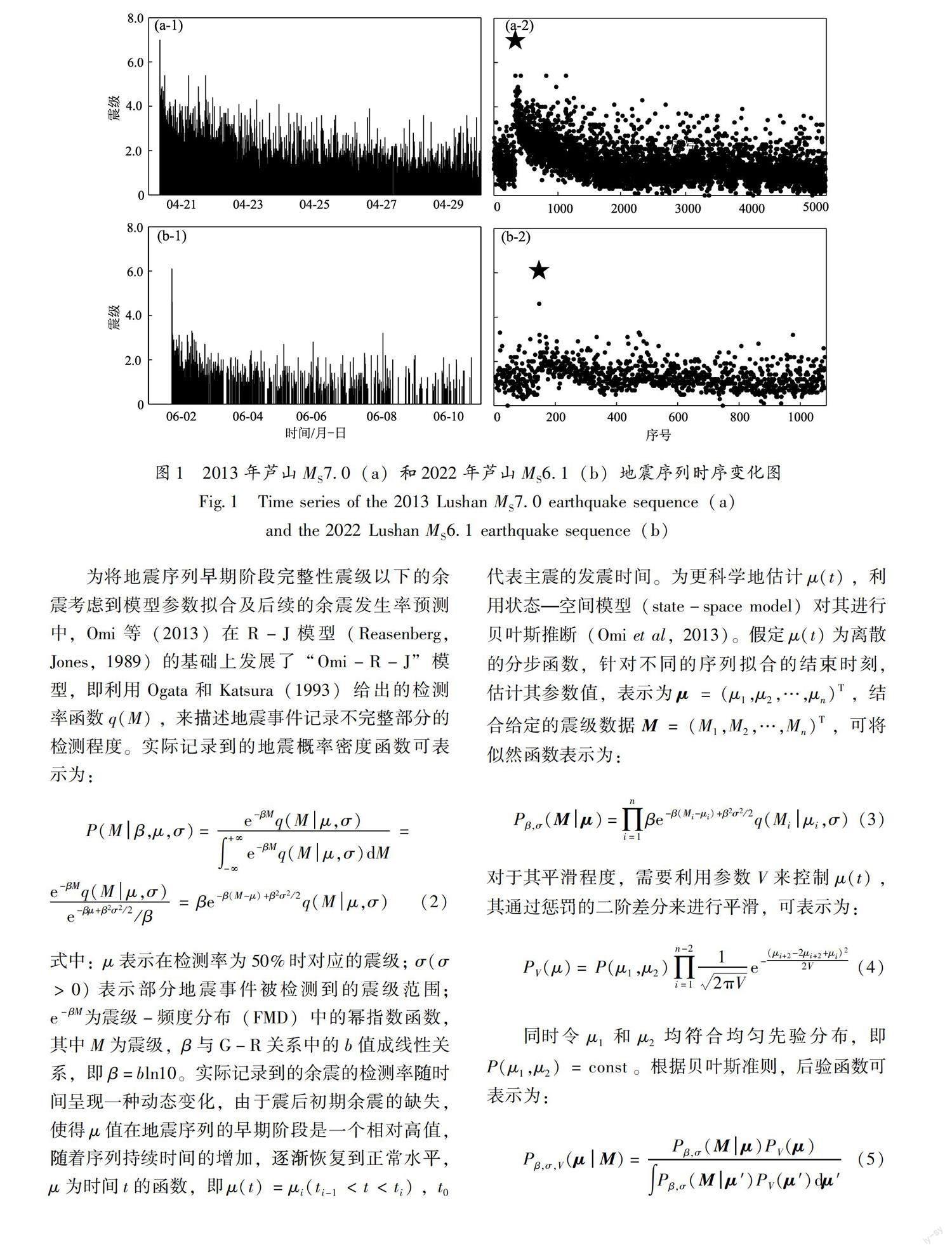
为对芦山两次强震的序列活动特征开展研究，本文使用了全国统一正式编目地震目录系统（中国地震台网中心，2022），并选用两次地震震后10 d内的数据。2013年芦山MS7.0地震后10 d内共记录到4 855次地震，其中5级以上余震4次，4.0～4.9级地震45次，3.0～3.9级地震244次；2022年芦山MS6.1地震后10 d内共记录到916次余震，其中4级以上地震1次，3.0～3.9级地震7次。两次地震序列的震级-时间（M-t）分布如图1a-1、b-1所示，震级-序号图如图1a-2、b-2所示。由此可知，两次芦山地震，特别是2013年MS7.0地震震后早期余震事件缺失严重。

2 地震序列检测率的变化特征

Reasenberg和Jones（1989）以余震衰减关系Omori-Utsu公式（Omori，1894；Utsu，1961）作为频次约束，以震级-频度分布关系式（Gutenberg，Richter，1944）作为强度约束，提出了余震短期概率预测模型。地震序列中，在t时刻震级不低于M的余震强度函数可表示为：

λ（t，M）=k（t+c）p×10-bM（1）

式中：t为余震的发震时刻；k控制余震及强余震活跃程度，与余震数目成正比；p的大小与序列的衰减快慢呈正相关关系；c用于调节主震发生后极短时间内余震记录的不完整性，与震源深度成负相关关系（Shebalin，Narteau，2017）；b与应力累积水平呈反比关系（Wiemer，Katsumata，1999；Enescu et al，2011）。

为将地震序列早期阶段完整性震级以下的余震考虑到模型参数拟合及后续的余震发生率预测中，Omi等（2013）在R-J模型（Reasenberg，Jones，1989）的基础上发展了“Omi-R-J”模型，即利用Ogata和Katsura（1993）给出的检测率函数q（M），来描述地震事件记录不完整部分的检测程度。实际记录到的地震概率密度函数可表示为：

P（Mβ，μ，σ）=e-βMq（Mμ，σ）∫+∞-∞e-βMq（Mμ，σ）dM=e-βMq（Mμ，σ）e-βμ+β2 σ2/2/β=βe-β（M-μ）+β2 σ2/2q（Mμ，σ）（2）

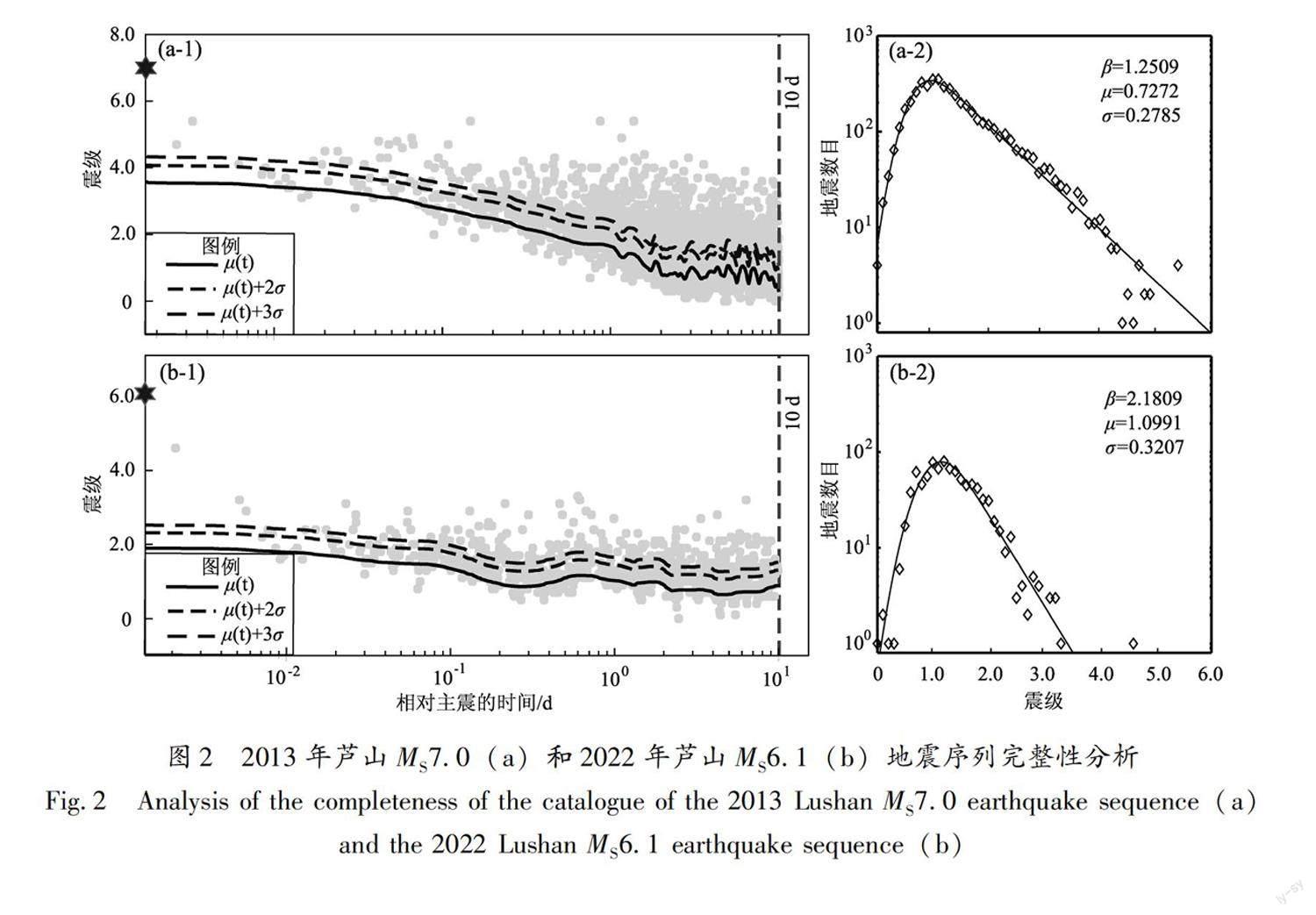
式中：μ表示在检测率为50%时对应的震级；σ（σ>0）表示部分地震事件被检测到的震级范围；e-βM为震级-频度分布（FMD）中的幂指数函数，其中M为震级，β与G-R关系中的b值成线性关系，即β=bln10。实际记录到的余震的检测率随时间呈现一种动态变化，由于震后初期余震的缺失，使得μ值在地震序列的早期阶段是一个相对高值，随着序列持续时间的增加，逐渐恢复到正常水平，μ为时间t的函数，即μ（t）=μi（ti-1

Pβ，σ（Mμ）=∏ni=1βe-β（Mi-μi）+β2 σ2/2q（Miμi，σ）（3）

对于其平滑程度，需要利用参数V来控制μ（t），其通过惩罚的二阶差分来进行平滑，可表示为：

PV（μ）=P（μ1，μ2）∏n-2i=112πVe-（μi+2-2μi+2+μi）22V（4）

同时令μ1和μ2均符合均匀先验分布，即P（μ1，μ2）=const。根据贝叶斯准则，后验函数可表示为：

Pβ，σ，V（μM）=Pβ，σ（Mμ）PV（μ）∫Pβ，σ（Mμ′）PV（μ′）dμ′（5）

Omi等（2013）利用牛顿迭代法（Newtons iteration）对超参数β、σ和V进行估计。在地震参数估计中，如果采取多次重复的计算方式，很难计算出参数估计中的偏差，获得较为稳定、可靠的参数估计值。针对数据不完整性问题。Veen和Schoenberg（2008）引入期望最大化（expectation-maximization，EM）算法来获得参数估计结果，本文也借鉴最大期望算法对参数进行优化。

Omi-R-J方法通过对每个地震事件逐步迭代的方式，可获得研究时段内的地震检测率随时间的变化。由于基于OK1993模型（Ogata，Katsura，1993）的Omi-R-J模型的μ是连续估计的参数，可分别用95.45%置信水平下完整记录的μ+2σ或者在99.74%置信水平下完整记录的μ+3σ，来近似描述最小完整性震级MC（Mignan，Woessner，2012；Iwata，2013）。图2a-1、b-1分别给出了2013年芦山MS7.0地震和2022年芦山MS6.1地震序列按照Ogata和Katsura（1993）模型的50%地震检测率μ（t）（50%）以及μ（t）+2σ（95.45%），μ（t）+3σ（99.74%）的分布情况。由图2a-1中的3个范围的检测率可知，2013年芦山地震序列的完备性随时间变化较为明显，震后缺失事件较多，余震记录事件有限，检测能力较低，在震后2 d逐渐恢复至稳定阶段，如果以μ（t）+3σ作为最小完整性震级，则被检测到余震的震级约为1.8级。2022年芦山地震序列的完备性随时间变化比2013年芦山地震序列平稳，如图2b-1所示，初期阶段μ（t）+3σ检测到余震的震级为2.5级，然后逐渐过渡至平稳时段的1.8级。造成芦山两次地震早期余震序列检测结果差异的原因为：一是2013年芦山地震震级较大，面波发育，震后早期更多的地震事件被“淹没”在主震中，较多的小地震无法被及时识别出来；二是近几年理记技术的发展和地震台网布局的优化使得更多的小震、微震被检测到，震后早期地震序列的检测率逐步提升。为更加定量化地分析检测率，本文基于0～10.00 d的观测数据，利用震级频度变化（FMD）进行了OK1993模型参数拟合，图2a-2、b-2分别给出了两次地震的拟合结果，菱形为地震目录的震级-频度分布，实线为OK1993模型拟合结果。拟合所得两组参数分别为β=1.250 9、μ=0.727 2、σ=0.278 5和β=2.180 9、μ=1.099 1、σ=0.320 7，擬合结果较好，验证了检测率变化的可靠性。

3 地震序列参数及不确定性分析

可靠稳定的地震序列参数是开展可操作的余震预测和地震危险性评估等研究的基础。Omi-R-J方法利用记录的全部余震事件，在震后短期内快速开展参数拟合，获得较为可靠的地震序列参数。通过利用状态—空间模型获得参数β、σ和V以及检测率的动态变化μ（t）后，考虑不完整地震记录的地震发生率函数可以表示为ν（t，M）=λ（t，M）q（Mμ（t），σ），与k、p、c相关的对数似然函数表示为：

lnL（k，c，p）=∑Mi≥Mclnν（ti，Mi）-∫∞McdM∫0Tdtν（t，M）（6）

式中：ti和Mi分别为在模型拟合的“学习时段” ［0，T］内发生的第i个余震的发震时刻与震级。

利用后验分布对Omi-R-J模型参数的不确定性进行检验、评估，参数的边际后验分布范围越宽（越窄），表示不确定性越大（越小）。为直观显示后验分布的离散图，采用马尔可夫链蒙特卡罗方法（Markov Chain Monte Carlo，MCMC）从后验分布中抽取Omi-R-J参数集，其优点是能够以几乎精准的方式评估不确定性，而无需对后验函数进行近似。采用Metropolis算法（Metropolis et al，1953）模拟一个多变量马尔可夫链，在高维后验分布中，可随机选择一个分量来进行转换。由于Omi-R-J模型参数的维数较少，同时创建所有参数分量来转换。为保证模型参数的独立性，需要重复模拟过程，直到平稳马尔可夫链的样本足够长，然后在时间间隔内对参数进行采样。本文基于Metropolis算法模拟10 000个参数集，然后选取1 000套（t=10，20，30，…，10 000）估算Omi-R-J模型参数。图3给出了2022年芦山MS6.1地震的参数估计值（黑十字）、采样参数集（灰点）以及采样参数的统计分布情况（柱状图），揭示了后验分布的复杂形式，以及参数之间的统计相关性。各数据采样点参数呈现出较好的优势分布，边际后验分布范围较窄，即存在较小的不确定性，揭示了参数拟合结果的可靠性。此外，各参数间存在一定的相关性，如反映应力水平的b（β=bln10）值与余震数目的k值具有较强的负相关，从另一侧面说明了应力水平较高的区域更易触发较多的强余震。

为更好地描述参数的变化特征，本文对芦山两次强震序列分别采用了连续、滑动的参数拟合，拟合起始时间为主震后0.05 d，以0.05 d为步长，持续增加至序列的10.00 d，进行了100个时段的滑动拟合。图4给出了拟合所得p值、c值、k值和b值随序列持续时间的变化图。由图可知，各参数值在序列的早期阶段变化相对剧烈，后期逐渐平稳。与基于ETAS模型所得的2013年芦山地震序列参数相比（蒋长胜等，2013），Omi-R-J模型在震后早期能够更早更快地获得较为稳定的序列参数。此外Omi-R-J方法曾应用于2008年四川汶川MS8.0地震（Bi，Jiang，2020a）、2017年四川九寨沟MS7.0地震（蒋长胜等，2018）、华北地区（Bi，Jiang，2020b）以及中国大陆其它板内地震（毕金孟等，2022），并与ETAS模型和R-J模型做了对比分析，发现Omi-R-J模型在震后早期能更快获得稳定参数。稳定时段，2013年四川芦山MS7.0地震的模型参数为p=1.017±0.026，c=0.014±0.005，k=0.029±0.006，b=0.784±0.015；2022年四川芦山MS6.1地震的模型参数为p=1.079±0.032，c=0.022±0.007，k=0.002±0.001，b=0.942±0.049，其中b值根据β=ln10×b所得。

由图4a-1、b-1可见，两个序列的p值相差不大，2013年芦山MS7.0地震序列在震后5 d内呈现一定的变化幅度，之后逐渐稳定在1.017左右，略低于基于ETAS模型的计算结果1.22（蒋长胜等，2013）；2022年芦山MS6.1地震序列p值在震后3 d内变化较为剧烈，之后逐渐稳定在1.079左右，较2013年芦山MS7.0地震序列变化更为剧烈；两个地震序列的p值与以中国大陆6.0级以上地震序列计算的平均值（0.984 2）和中值（1.020 2）基本接近（毕金孟等，2022），展示了相对正常的序列衰减过程。

由图4a-2、b-2可知，两个序列的c值相差不大，2013年芦山MS7.0地震序列稳定值趋向于0.014附近，2022年芦山MS6.1地震序列稳定值趋向于0.022附近，略大于2013年芦山MS7.0地震序列稳定值。由于压力和温度通常都随着深度的增加而增加，c随深度的增加而减小（Shebalin， Narteau，2017）。基于区域地震台网记录，利用“裁剪—粘贴”（CAP）方法对两次芦山地震进行矩心矩张量反演得到2013年芦山MS7.0地震的震源矩心深度約为14 km（吕坚等，2013），2022年芦山MS6.1地震的最佳矩心震源深度约16 km（梁皓等，2022）。同样，基于双差定位的方法测得两次地震事件的震源深度分别为17.6 km和20 km（房立华等，2013；中国地震局地球物理研究所，2022），两种方法测得两次地震震源深度略有不同，c值的差异也证明了两次地震的震源深度存在一定的差异。

由图4c-1、c-2可见，两个序列的k值存在很大的差异，2013年芦山MS7.0地震的地震序列k值在震后早期阶段（4 d内）变化较为剧烈，随后缓慢减小至0.029附近；2022年芦山MS6.1地震序列R值在震后早期阶段（3 d内）基本稳定在0.002附近，较2013年芦山MS7.0地震地震序列值明显偏小。k值控制余震的活跃程度，在中国大陆板内地震中与强余震数量呈正相关关系（毕金孟等，2022），这很大程度上取决于单个余震序列，且与主震震级关系不大，这也解释了2013年芦山MS7.0地震较为发育的余震序列和2022年芦山MS6.1地震序列余震尤其是强余震数量相对较少的原因。

由图4d-1、d-2可见，两个序列的b值存在一定的差异，在 震后初期阶段（2 d内）呈现出一定的变化，之后2013年芦山MS7.0地震序列b值逐渐趋于0.784附近，与基于最大似然法获得的b值结果接近（蒋长胜等，2013），2022年芦山MS6.1地震序列b值逐渐趋于0.942附近，明显高于2013年芦山MS7.0地震序列。2013年芦山MS7.0地震序列的b值低于中国大陆的均值线（0.849 4）和中值线（0.830 6）（毕金孟等，2022），显示出了余震区较高的应力水平，而2022年芦山MS6.1地震序列b值高于中国大陆的b值均值线和中值线，表明该地区的应力水平已得到很大程度的释放，也表明了该地区发生强余震的风险大大降低。2013年芦山MS7.0地震序列b值呈现出先上升后下降的过程，反映了主震后应力得到释放，然后继续积累，继而触发余震的过程，而2022年芦山MS6.1地震序列b值呈现出先下降后逐渐上升最终趋于稳定的过程，反映了震后短暂的应力调整后就持续释放的过程。

4 余震预测结果及效能评估

基于上述的序列参数拟合结果，通过式（1）计算在M>MP和任意时间间隔［t2，te］内的余震预测数目：

N=∫tet2∫∞Mpλ（t，M）dtdM（7）

为检验芦山两次强震在震后初期（1 d内）的“M-3”强余震发生率的预测效能，即距主震震级3个震级档以内的余震事件视为强余震，选用CSEP计划中针对地震数检验的N-test方法（Kagan，Jackson，1995；Schorlemmer et al，2007；Zechar，2010）来验证Omi-R-J模型预测的地震数目与实际数目的偏离程度，并利用有效显著性水平αeff=0.025对N-test检验结果进行单边检验，当δ1<αeff时，表示预测强余震数目过少；当δ2<αeff时则表示预测强余震数目过多。

以芦山两次地震后0.20～1.20 d、0.20～3.20 d的强余震预测为例，图5a分别给出了基于Omi-R-J模型对芦山两次地震未来1 d（图5a-1、a-2）、3 d（图5a-3、a-4）预测结果与实际观测结果在震级-累积频次上的比较，图中黑色圆点为实际观测结果，黑色线段为预测结果，灰色阴影为预测结果的95%置信区间。图5b分别给出了芦山两次地震未来1 d（图5b-1、b-2）、3 d（图5b-3、b-4）距主震震级3个震级档的预测结果与实际观测结果在时间-累积频次上的比较，图中黑色曲线为实际观测结果，灰色曲线为预测结果，灰色虚线标出了预测结果的95%置信区间，黑色垂直虚线标出了预测起始时刻。实际发生地震数均在预测数的95%置信区间，其评分值依次为［0.821 6，0.256 1］、［0.425 1，0.758 0］、［0.830 8，0.227 7］、［0.748 4，0.423 4］，显示了较好的预测效能。由于大量的强余震发生在主震后的数天内，尤其是震后1～3 d内，是减轻地震灾害风险的“黄金时间”，因此，此次仅针对震后1 d内数据分别在［0～0.2，0～0.4，0～0.6，0～0.8，0～1.0］时段开展震后1 d和3 d的强余震（M>3）发生率预测及“量化”的效能评估，其结果见表1，在不考虑预测时段未发生地震的情况下，仅有一次地震事件未通过N-Test检验，出现预测过少的情况，其他时段均表现出了较好的预测效能。

5 结论

为分析2013年芦山MS7.0和2022年芦山MS6.1两次强震的序列活动特征和震后初期的强余震预测效能，本文基于Omi-R-J模型，利用余震序列早期阶段大量不完整的小震级事件，对序列的检测率变化和序列参数的变化进行了对比研究，并在震后初期（1 d内）开展强余震发生率预测以及利用针对地震数的N-test方法进行效能评估，得到以下结果：

（1）2013年芦山MS7.0地震序列的完备性随时间变化明显，震后早期阶段余震记录事件有限，检测能力较低，此后两个地震序列的完备性逐渐恢复，至稳定阶段μ（t）+3σ（99.73%）检测到的余震的震级约为1.8。

（2）从总体上看，由于地震震级大小、发震构造等方面的不同，芦山两次地震的参数变化以及稳定时段的参数值均存在一定的差异。在震后早期阶段，2013年芦山MS7.0地震序列参数变化较为剧烈且达到稳定时段所需时间较长，这或许是与其序列较复杂有关。2013年芦山MS7.0地震稳定时段的序列参数为p=1.017±0.026，c=0.014±0.005，k=0.029±0.006，b=0.784±0.015；2022年芦山MS6.1地震序列参数为p=1.079±0.032，c=0.022±0.007，k=0.002±0.001，b=0.942±0.049。

（3）对比两次芦山地震序列參数发现，p值相差不大，且与中国大陆6.0级以上地震序列的平均值和中值接近，展示了相对正常的序列衰减过程；两次地震的震源深度的不同使得c值存在略微差异；两次地震序列的k值存在很大差异——2013年芦山MS7.0地震序列的k值明显大于2022年芦山MS6.1地震序列，这与2013年芦山地震较为发育的余震或强余震有关；两次地震序列的b值存在一定的差异，2013年芦山MS7.0地震序列的b值小于2022年的芦山MS6.1地震序列，表明2013年之后芦山地区仍是高应力地区，依然存在发生中强震或强余震的风险，而2022年芦山MS6.1地震之后，应力得到释放，应力水平处于一个相对较低的状态。

（4）利用N-test方法对芦山两次地震震后初期强余震预测结果的效能开展评估，结果显示，Omi-R-J模型对两个地震序列震后初期阶段展示了较好的预测效能，在基于震后1 d内的数据开展的分段和分尺度预测中，两个序列对未来1 d预测，仅存在一次预测失效的情况，而对未来3 d的预测，不存在预测失效的情况，这证明了Omi-R-J模型可以在震后初期阶段就能开展较为有效的余震预测。

本文研究中使用了中国地震台网中心“全国地震编目系统”提供的“统一正式目录”，中国地震局地球物理研究所蒋长胜研究员和日本东京大学生产技术研究所Takahiro Omi博士为本研究提供了程序和技术支持，评审专家提出了诸多建设性修改建议，对稿件质量提升帮助很大，在此一并表示感谢。

参考文献：

毕金孟，蒋长胜，来贵娟，等.2022.中国大陆强震的早期余震概率预测效能评估与制约因素［J］.地球物理学报，65（7）：2532-2545.

房立华，吴建平，王未来，等.2013.四川芦山MS7.0级地震及其余震序列重定位［J］.科学通报，58（20）：1901-1909.

蒋长胜，毕金孟，王福昌，等.2018.利用早期余震预测的Omi-R-J方法对2017年四川九寨沟MS7.0地震的应用研究［J］.地球物理学报，61（5）：2099-2110.

蒋长胜，庄建仓，龙锋，等.2013.2013年蘆山MS7.0地震序列参数的早期特征：传染型余震序列模型计算结果［J］.地震学报，35（5）：661-669.

李传友，徐锡伟，甘卫军，等.2013.四川省芦山MS7.0地震发震构造分析［J］.地震地质，35（3）：671-683.

李勇，周荣军，赵国华，等.2013.龙门山前缘的芦山地震与逆冲—滑脱褶皱作用［J］.成都理工大学学报（自然科学版），40（4）：353-363.

梁皓，戴丹青，杨志高，等.2022.2022年6月1日四川芦山6.1级地震应急产品及震源参数初步分析［J］.中国地震，38（2）：360-369.

吕坚，王晓山，苏金蓉，等.2013.芦山7.0级地震序列的震源位置与震源机制解特征［J］.地球物理学报，56（5）：1753-1763.

苏金蓉，郑钰，杨建思，等.2013.2013年4月20日四川芦山M7.0级地震与余震精确定位及发震构造初探［J］.地球物理学报，56（8）：2636-2644.

徐锡伟，陈桂华，于贵华，等.2013a.芦山地震发震构造及其与汶川地震关系讨论［J］.地学前缘，20（3）：11-20.

徐锡伟，闻学泽，韩竹军，等.2013b.四川芦山7.0级强震：一次典型的盲逆断层型地震［J］.科学通报，58（20）：1887-1893.

张岳桥，董树文，侯春堂，等.2013.四川芦山2013年MS7.0地震发震构造初步研究［J］.地质学报，87（6）：747-758.

中国地震局地球物理研究所.2022.2022年6月1日四川芦山6.1级地震的震源特征［EB/OL］.（2022-06-02）［2022-06-28］.https：//www.cea-igp.ac.cn/kydt/279024.html.

中国地震台网中心.2022.全国地震编目系统地震目录［DB/OL］.（2022-06-25）［2022-06-25］.http：//10.5.160.18/console/exit.action.

周荣军，李勇，苏金蓉，等.2013.四川芦山MW6.6级地震发震构造［J］.成都理工大学学报（自然科学版），40（4）：364-370.

Bi J M，Jiang C S.2020a.Comparison of early aftershock forecasting for the 2008 Wenchuan MS8.0 earthquake［J］.Pure and Applied Geophysics，177（1）：9-25.

Bi J M，Jiang C S.2020b.Research on the forecasting strategy of early aftershocks in North China［J］.Annals of Geophysics，63（4）：SE441.

Enescu B，Enescu D，Ito K.2011.Values of b and p：their variations and relation to physical processes for earthquakes in Japan and Romania［J］.Romanian Journal of Physics，56（3-4）：590-608.

ERC（Earthquake Research Committee report）.2016.Information on earthquake forecasting after a large earthquake［J/OL］.（2016-08-19）［2022-07-02］.https：//www.jishin.go.jp/main/yosoku_info/honpen.pdf.

Gerstenberger M C，Rhoades D A，McVerry G H.2016.A hybrid time-dependent probabilistic seismic-hazard model for Canterbury，New Zealand［J］.Seismological Research Letters，87（6）：1311-1318.

Gerstenberger M C，Wiemer S，Jones L M，et al.2005.Real-time forecasts of tomorrows earthquakes in California［J］.Nature，435（7040）：328-331.

Gutenberg R，Richter C F.1944.Frequency of earthquakes in California［J］.Bulletin of the Seismological Society of America，34（4）：185-188.

Iwata T.2008.Low detection capability of global earthquakes after the occurrence of large earthquakes：Investigation of the Harvard CMT catalogue［J］.Geophysical Journal International，174（3）：849-856.

Kagan Y Y，Jackson D D.1995.New seismic gap hypothesis：five years after［J］.Journal of Geophysical Research：Solid Earth，100（B3）：3943-3959.

Lippiello E，Cirillo A，Godano C，et al.2019.Post seismic catalog incompleteness and aftershock forecasting［J］.Geosciences，9（8）：355.

Marzocchi W，Lombardi A M，Casarotti E.2014.The establishment of an operational earthquake forecasting system in Italy［J］.Seismological Research Letters，85（5）：961-969.

Metropolis N，Rosenbluth A W，Rosenbluth M N，et al.1953.Equation of state calculations by fast computing machines［J］.The Journal of Chemical Physics，21（6）：1087-1092.

Michael A J，McBride S K，Hardebeck J L，et al.2020.Statistical seismology and communication of the USGS operational aftershock forecasts for the 30 November 2018 MW7.1 Anchorage，Alaska，earthquake［J］.Seismological Research Letters，91（1）：153-173.

Mignan A，Woessner J.2012.Estimating the magnitude of completeness for earthquake catalogs［J/OL］.（2012-05）［2022-07-02］Community Online Resource for Statistical Seismicity Analysis，1-45.http：//www.corssa.org/export/sites/corssal.galleries/articlespaf/Migan-Woessner-2012-CORSSA-Magitude-of-completeness.pdf-2063069299.pdf.

Nanjo K Z，Tsuruoka H，Yokoi S，et al.2012.Predictability study on the aftershock sequence following the 2011 Tohoku-Oki，Japan，earthquake：first results［J］.Geophysical Journal International，191（2）：653-658.

Ogata Y，Katsura K，Falcone G，et al 2013.Comprehensive and topical evaluations of earthquake forecasts in terms of number，time，space，and magnitude［J］.Bulletin of the Seismological Society of America，103（3）：1692-1708.

Ogata Y，Katsura K.1993.Analysis of temporal and spatial heterogeneity of magnitude frequency distribution inferred from earthquake catalogues［J］.Geophysical Journal International，113（3）：727-738.

Ogata Y，Katsura K.2006.Immediate and updated forecasting of aftershock hazard［J］.Geophysical Research Letters，33（10）：L10305.

Ogata Y.1983.Estimation of the parameters in the modified Omori Formula for aftershock frequencies by the maximum likelihood procedure［J］.Journal of Physics of the Earth，31（2）：115-124.

Ogata Y.1989.Statistical model for standard seismicity and detection of anomalies by residual analysis［J］.Tectonophysics，169（1-3）：159-174.

Omi T，Ogata Y，Hirata Y，et al.2013.Forecasting large aftershocks within one day after the main shock［J］.Scientific Reports，3（1）：2218.

Omi T，Ogata Y，Shiomi K，et al.2016.Automatic aftershock forecasting：a test using real-time seismicity data in Japan［J］.Bulletin of the Seismological Society of America，106（6）：2450-2458.

Omi T，Ogata Y，Shiomi K，et al.2019.Implementation of a real-time system for automatic aftershock forecasting in Japan［J］.Seismological Research Letters，90（1）：242-250.

Omori F.1894.On aftershocks of earthquakes.Journal of the College of Science［J］.Imperial University of Tokyo，7：111-200.

Peng Z G，Zhao P.2009.Migration of early aftershocks following the 2004 Parkfield earthquake［J］.Nature Geoscience，2（12）：877-881.

Reasenberg P A，Jones L M.1989.Earthquake hazard after a mainshock in California［J］.Science，243（4895）：1173-1176.

Reverso T，Steacy S，Marsan D.2018.A hybrid ETAS-Coulomb approach to forecast spatiotemporal aftershock rates［J］.Journal of Geophysical Research：Solid Earth，123（11）：9750-9763.

Schorlemmer D，Gerstenberger M C，Wiemer S，et al 2007.Earthquake likelihood model testing［J］.Seismological Research Letters，78（1）：17-29.

Schorlemmer D，Werner M J，Marzocchi W，et al 2018.The collaboratory for the study of earthquake predictability：Achievements and priorities［J］.Seismological Research Letters，89（4）：1305-1313.

Shebalin P，Narteau C.2017.Depth dependent stress revealed by aftershocks［J］.Nature Communications，8（1）：1317.

Utkucua M，Süleyman S，Nalbant B，et al.2021.The June 12，2017 M6.3 Karaburun-Lesvos earthquake of the Northern Aegean Sea：Aftershock forecasting and stress transfer［J］.Tectonophysics，814：228945.

Utsu T，Ogata Y，Matsuura R S.1995.The centenary of the Omori formula for a decay law of aftershock activity［J］.Journal of Physics of the Earth，43（1）：1-33.

Utsu T.1961.A statistical study of on the occurrence of aftershocks［J］.Geophysical Magnitude，30：521-605.

Veen A，Schoenberg F P.2008.Estimation of space-time branching process models in seismology using an em-type algorithm［J］.Journal of the American Statistical Association，103（482）：614-624.

Wiemer S，Katsumata K.1999.Spatial variability of seismicity parameters in aftershocks zones［J］.Journal of Geophysical Research，104（13）：13135-13151.

Zechar J D.2010.Evaluating earthquake predictions and earthquake forecasts：a guide for students and new researchers［J/OL］.（2010-09-01）［2022-06-29］.http：//www.corssa.org/export/sites/corssa/.galleries/articles-pdf/zechar.pdf.

Comparative Analysis of the Activity Characteristics and the AftershockForecasting Efficiency of Two Earthquake Sequences in Lushan

BI Jinmeng1，2，SONG Cheng1，MA Yong1

（1.Tianjin Earthquake Agency，Tianjin 300201，China）

（2.Institute of Geophysics，China Earthquake Administration，Beijing 100081，China）

Abstract

We used the Omi-R-J model，which can fully make use of the information of small earthquakes，to compare and analyze the characteristics of the activity of two strong-earthquake sequences in Lushan，Sichuan Province.we found that the completeness of the Lushan MS7.0 earthquake sequence in 2013 changed more obviously with time than that of the Lushan MS6.1 earthquake sequence in 2022.In the early period after the two mainshocks，a few aftershocks were detected by the Omi-R-J model，and the completeness magnitude detected in the stable period of the two earthquake sequences was both about 1.8.The difference between the p-values of the two Lushan earthquake sequences was small，showing a relatively normal attenuation process of the two sequences.k-value of the MS7.0 earthquake sequence was significantly larger than that of the MS6.1 sequence；this may be the result of the relatively more aftershocks or the strong aftershocks of the MS7.0 sequence.b-value of the MS7.0 earthquake sequence was smaller than that of the MS6.1 sequence；this indicated that Lushan area was still in a high-stress state after the 2013 MS7.0 earthquake，but after the 2022 MS6.1 earthquake the stress reached a relatively low level.The efficiency evaluation of the N-test method showed that in the initial stage of the two earthquake sequences the aftershock forecasting was efficient.Based on the next days data，the forecasting of the aftershocks on the second day after the mainshock only failed once，while the forecasting of the aftershocks of the successive 3 days after the second day of the mainshock did not fail.

Keywords：the Lushan earthquake；the Omi-R-J model；detection rate；sequence parameters；effectiveness evaluation of aftershork forecasting

收稿日期：2022-07-09.

基金項目：地震预测开放基金（XH23072D）；中国地震局震情跟踪定向工作任务（2022010116，2020010104）.

第一作者简介：毕金孟（1989-），工程师，主要从事地震活动性研究.E-mail：jinmengbi@126.com.

毕金孟，宋程，马永.2023.芦山两次强震序列活动特征及余震预测效能对比分析［J］.地震研究，46（2）：204-215，doi：10.20015/j.cnki.ISSN1000-0666.2023.0021.