基于复杂网络的深市行业板块分析

宋义若

【摘  要】论文建立在复杂网络的基础上，对行业板块指数构建网络图来分析之间的相关关系。股市的变动变化莫测，在对宏观绩效、经济形势以及微观层面研究的基础上，论文提出从行业分类板块之间观察板块之间的联系，从而观测对股市整体的影响。通过对哪个板块的带动效应最为明显以及哪个板块在股市中最能起到稳定作用的分析，在论文实证结果的验证之上，得出中国深市行业板块中带动效应几乎均同的结论。

【关键词】复杂网络；行业板块；带动效应

【中图分类号】F832.5                                             【文献标志码】A                                                 【文章编号】1673-1069（2023）02-0051-03

1 研究背景

新冠肺炎蔓延肆虐全球，对人类生活模式、社会生产方式和国际社会之间的交流关系都产生了强烈的冲击。在全球产业链以及供应链都受到严重冲击的条件下，全球的经济陷入大幅衰退。包括美国在内的西方发达国家为维持经济体系的稳定，重拾量化宽松政策。在这种国际形势背景下，中国抗击疫情成果显著，经济恢复迅速，成为世界主要经济体中一道靓丽的风景线。

IMF的财报指出，中国是2020 年唯一一个世界范围内实现经济正增长的国家，这种特殊性在股市上表现得尤为明显。回望2020 年的中国股市和世界股市变动，美国创造股市跌停历史，中国继2019 年股市变动与新冠肺炎疫情的影响下，沪市指数甚至突破了3 400 点的大关，创造了2020年以来最高的投资回报率。分析股票市场的这一变动以及中国股票市场与世界股票市场的差异，什么因素在其中起作用呢？

经济形势的变动以及政策信息无疑会影响股市的变动，事件研究法（Event Study）是一种研究市场上某时间发生后股价是否产生波动的统计方法，运用事件研究法研究相关政策对于股票市场的整体冲击以及对于某个板块冲击的文章很多，也可以证明股价的变动的确与经济形势的变动之间存在相关关系，但并没有统一的一致性结论，统一指向乐观明确的态度或是什么。股市价格对于市场信息的反应也是检测股票市场有效性的基础。我国资本市场改革进展成效显著，对股市有效性的验证也趋向于多样性发展。在这些研究的基础上，本文重在探索股市变动与板块之间的联系。板块投资作为现代投资中一种重要分散风险的理念显得越发重要。那么在投资者投资的过程中，哪个是稳定性板块？哪个是领涨型板块？这一判断对于投资者的行为选择有很大的借鉴意义。

2 研究现状及内容

中国股票市场的供需矛盾、结构矛盾以及市场参与者的不成熟等原因，使政府加强了对股票市场的监管和调控，政策干预及调控成为市场波动的一个主要影响因素，中国股市一直有所谓的“政策市”之称，呈现出一种特殊的游戏规则。股市政策较大程度地影响了中国股市的板块轮动，股市运行受短期性政策事件的影响极大。刘伟和黄少安（2020）在实证中证实了股市价格变化与宏观经济变量之间存在长期因果关系，短期內的网络效应比较复杂，主要从宏观层面上对股票价格的变动作出了阐述。

从所属板块的角度上来看，何诚颖（2001）提出中国的股市具有“板块现象”，也就是与事件相关联的股票价格的变动会具有一致性，即“板块联动现象”。“板块联动现象”是指在某时期内，同属于某一基本面类别或概念因素的股票会出现同涨同跌的现象。但板块现象中呈现的股票市场走势一致性可能会导致以板块为范围出现系统性风险，因此其对市场走势的影响可能远超其对基本面的影响程度。另外，在关于板块的研究中，除板块的“联动效应”外，还有创新型板块扩展、板块的聚类分析以及我国多层次资本市场的划分，但某些板块事件实际上对基本面没有实质影响，如以地域为划分的板块，因此运用网络分析方法对行业板块之间的联系进行分析，可以得出比较直观的结果。

目前的网络分析方法主要可以分为规则网络、随机网络和复杂网络。规则网络为最简单的网络模型，它是指系统中各元素之间的关系可以用一些规则的结构表示，也就是说网络中任意两个节点之间的联系遵循既定的规则，通常每个节点的近邻数目都相同。随机网络，又称随机图，是指通过随机过程制造出的复杂网络。 最典型的随机网络是保罗·埃尔德什和阿尔弗雷德·雷尼提出的ER模型。复杂网络（Complex Network），是指具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络。周涛等（2005）指出随机网络和复杂网络的运用较为普遍。随机网络是以节点之间的概率决定网络边的模型，复杂网络具有与前二者不同的统计特征。鉴于指数回报率指标之间的相关系数不属于概率性质的随机模型，本文采用复杂网络的方法对行业板块之间的关系进行分析。

3 数据及方法

该部分对本文所选取的数据来源和处理数据的步骤进行分析，详细列举出了本文所运用的公式和指标。公式为计算股价日收益率的对数收益率公式，之后根据计算出的日收益率将各行业间的相关系数构建成 16×16 的矩阵，为后面的网络图绘制做好数据准备。

3.1 数据选取

本文选取深圳证券交易所上市的行业分类指数，共包含农林、采矿、制造、水电、建筑、批零、运输、餐饮、IT、金融、地产、商务、科研、公共、文化以及综企 16 个指数板块。从国泰安（CSMAR）数据库中提取从 2020 年 1 月 1 日开始到 2020 年 12 月 31日的指数收盘数据，共覆盖 245×16 共 3 920 个数据。

3.2 公式和指标构建

为了构建复杂网络，首先计算指数i在第t天的对数收益率：

ri（t）=lnpi（t）-lnpi（t-1）                 （1）

式中，ri（t）是指数i在第t天的对数收益率，lnpi（t）是指指数i在第t天的指数收盘价格。

任意两个指数作为网络的节点，节点i和j之间的相关系数作为网络的边来建立网络，两个节点之间相关系数的公式为：

cij     （2）

式中，ri是指数i的平均收益率，同理，rj是指数j的平均收益率。

3.3 衡量网络图的指标

3.3.1 度分布

度分布（Degree Distribution）在图论和网络中，度（degree）是指网络（图）中一个点与其他点的连接数量，度分布（Degree Distribution）就是整个网络中，各个点的度数量的概率分布。节点度分布是一个重要的参数，节点i的度表示所有与这个节点有连边的节点数。本文网络中节点的度具体表现为一个板块与其他板块之间的连接关系和紧密程度。节点度越大，则这个板块在网络中就越重要。

3.3.2 平均路径长度（距离）

网络中两个节点之间的距离定义为连接这两个节点的平均距离边数，是用来衡量网络密度的重要指标。网络的平均路径长度（Average path length）L定义为任意两个节点之间的距离的平均值，网络的平均路径长度也称为网络的特征路径长度（Characteristic Path Length）或平均距离（Average Distance）。即：

L=     （3）

式中，N为网络节点数。

3.3.3 中心势

中心势（Centralization）刻画整个网络各个点的差异性程度，因此一个网络只有一个中心势。网络中心势越高，网络之间的相关性就越强，表明该网络之间的集中趋势就越大。

4 实证结果及解释

4.1 实证结果

首先，通过式（1）将指数收盘价格进行了对数收益化处理，然后通过式（2）计算出指数与指数间的相关系数。相关系数构建出 16×16 的矩阵后，运用 ucinet 软件将表1绘制成网络图（见图1）。

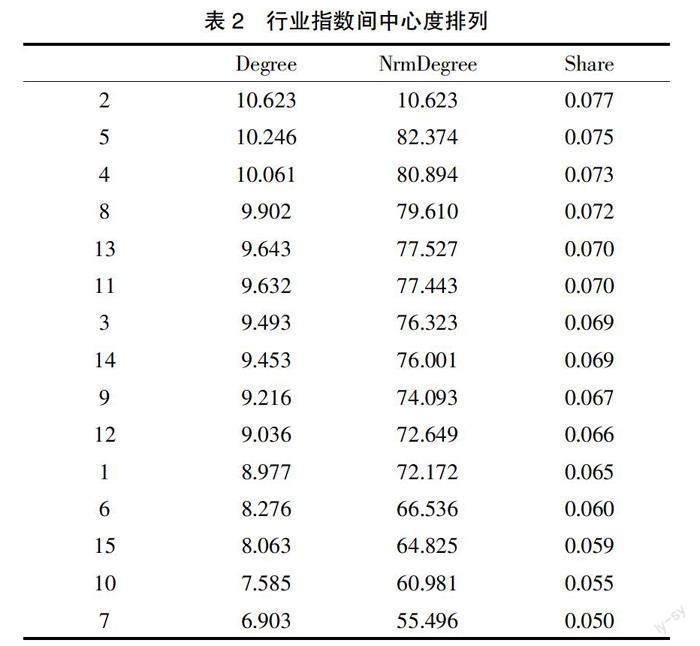
在描述性统计中，指标分别为度数中心度和网络份额。度数中心度是指在一个社会网络中，与其他节点相互联系的节点数，可以划分为绝对中心度（Degree）和相对中心度（NrmDegree），二者之间的区别是后者是前者的标准形式。从表2结果可以看出，数字 2代码也就是采矿业的代码在网络中占据最高的中心度，其次为建筑以及水电行业。相比较各个行业指数的中心度数值以及网络份额分布，可以看出，网络中各行业指数中心度差别不大，在网络中所占份额相差也不大。

在对网络中心度的数据进行分析之后，本文进一步对相关系数的统计性结果进行了汇总。其中包括 16 个指数之间的平均值、协方差，最大值以及最小值等因素。在描述了各有关统计项变量的中心度之后，我们还对本文网络整体的中心性做出了数据性的统计。统计结果如表3所示。在统计结果的基础之上，网络中心性的数值为 13.76%，异质性，即网络的不纯度为6.75%，归一化标准程度为 0.09%。

4.2 实证结果的解释及不足

本文对于行业板块网络图的绘制只建立在对数收益率以及相关系数矩阵的基础上，对于行业板块之间的因果关系并没有进行分析和建模。因此得出的网络图结果只能反映在无序状态下各行业板块在股市中所占据的整体比重。

根据本文上述实证结果可以看出，行业板块之间相关性在建立于本文假设的基础上几乎相差不大。除了农林板块、批零板块、文化板块以及运输板块，相对于其他板块的带动效应而言可能没有那么显著。也是基于这种统计结果，我们可以得出板块带动效应可以在所有板块之间都可以表现得一样显著。

5 结论與展望

本文基于复杂网络的方法，整理了国泰安数据库中的行业指数板块数据之后，在计算对数收益率和指数之间相关系数的基础上对指数板块之间的关系构建了复杂网络。在复杂网络的分析中，主要考虑了网络的中心度问题。基于每个行业板块的中心度指标，我们可以得出每个行业板块的带动效应和影响效应在本文所假设的条件下都大致相似。然后对整个网络的中心度以及异质性指标作出分析，可以看出，整体网络的中心度程度较低，异质性较为明显。这一结果的产生可以解释为本文的模型设置不够规范。在本文设置公式以及网络模型之前，没有对板块之间的因果关系进行检测。

未来的研究方向可以从缩小时间跨度、检验板块之间的因果关系以及将复杂网络放置在标准模型下进行检验，进而对无标度网络和小世界效应展开分析。

【参考文献】

【1】刘伟，黄少安.股票市场与宏观经济的动态相关性研究——基于金砖五国的实证分析[J].济南大学学报（社会科学版），2020，30（03）：114-128+160.

【2】何诚颖.中国股市“板块现象”分析[J].经济研究，2001（12）：82-87.

【3】周涛，柏文洁，汪秉宏，等.复杂网络研究概述[J].物理，2005（01）：31-36.