高阶灾难保险的价格

VIX期权是芝加哥期权交易所2006年推出的基于波动率指数的期权。VIX看涨期权和标准普尔500指数（SPX）看跌期权对投资者来说都是“灾难保险”，二者功能显然高度重合。为什么在SPX期权已广泛交易的情况下，投资者还对VIX期权有需求呢？本文介绍的作者与合作者撰写的《高阶灾难保险的价格：VIX期权的例子》研究了该问题。

衍生品的一个重要作用是提供完全市场，即帮助投资者实现传统资产无法实现的投资。投资者交易衍生品Z，说明衍生品Z能帮助他们实现传统资产X和衍生品Y都无法实现的投资。芝加哥期权交易所（Chicago Board Options Exchange，简称CBOE）在1983年、2004年、2006年相继推出标准普尔500指数（S&P 500 Index，简称SPX）期权、波动率指数（Volatility Index，简称VIX指数）期货、VIX期权。每一个都大受追捧，说明这些衍生品分别起到不同的作用。VIX指数衡量的是SPX波动性，VIX期货使投资者能直接投资股市波动性。VIX期权是基于VIX的衍生品，因此和VIX期货功能部分重叠。“波动反馈效应”导致SPX和VIX强烈负相关，因此当股灾发生时，VIX指数会猛烈上涨。VIX看涨期权和SPX看跌期权因此都是“股灾保险”，功能再次高度重叠。因此，一个重要问题是：VIX期权到底有什么超越VIX期货和SPX期权之处？

尽管原有文献中已经有一些VIX期权定价模型，但关于上述经济学问题没有系统的回答。笔者和威斯康星大学比约恩·埃拉克（Bjorn Eraker）教授合作撰写的2022年12月刊发于《金融学期刊》（Journal of Finance）的论文《高阶灾难保险的价格：VIX期权的例子》（The Price of Higher Order Catastrophe Insurance： The Case of VIX Options）（下简称“论文”）研究了这一问题。

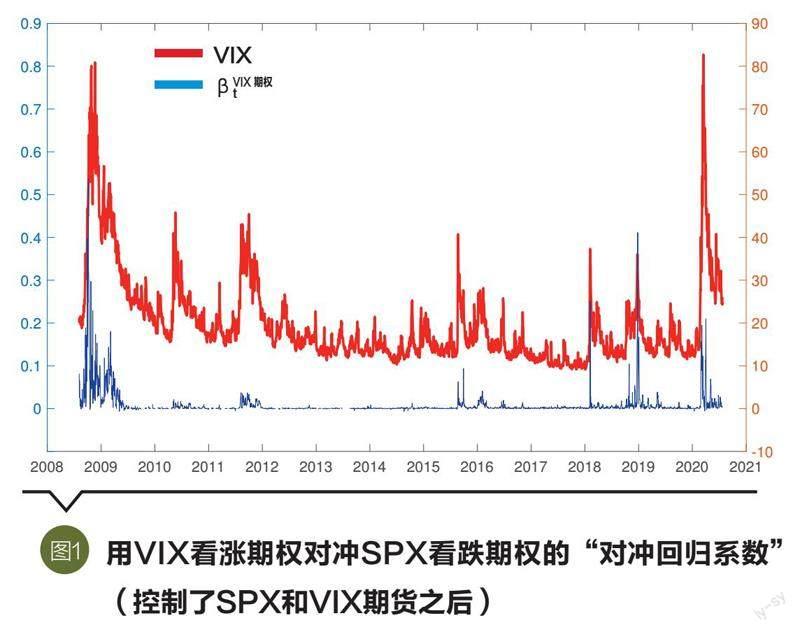
论文实证部分通过三种方法来研究上述衍生品之间的关系。第一，对冲回归（Hedge Regression）。假设现在我们要对冲SPX看跌期权，教科书的方法是德尔塔对冲（Delta hedge）［采用SPX指数交易基金（Exchange Traded Funds，简称ETFs）］和维加对冲（Vega hedge）（采用VIX期货）。论文作者发问：当控制了这两种传统的对冲工具后，VIX看涨期权还能帮助对冲SPX看跌期权吗？论文作者发现，该问题的答案显著地随经济周期或市场环境的变化而变化。在“衰退（高股市波动）”时期，二者关系紧密，VIX期权能显著地帮助对冲SPX期权。在“扩张（低股市波动）”时期，二者关系微弱，VIX期权几乎不能帮助对冲SPX期权。第二，主成分分析（Principal Component Analysis，简称PCA）。不同于原有文献中用PCA来分析股票或债券的横截面数据，论文作者将SPX期权和VIX期权按虚实程度（moneyness）分类，然后使用PCA来研究“股灾保险市场（SPX看跌和VIX看涨期权）”的因子结构。作者发现，前四个主成分，即SPX的水平（SPX level）、SPX的偏离度（SPX skewness）、SPX的尾部（SPX tail）、SPX的波动率（SPX volatility）能解释绝大部分SPX和VIX期权的变动。但是不同虚实程度的SPX、VIX期权在四个主成分上的承载很不相同。这和之前的实证发现相符，都说明VIX期权和SPX期权的功能不完全重叠。第三，期权隐含波动率曲线。原有文献发现SPX期权的隐含波动率曲线呈现“凸性微笑”（convex smile），且这一特征相当稳定，并不太随市场环境的变化而变化。论文作者发现，VIX期权的隐含波动率曲线在“衰退”时期呈现“凸性微笑”，在“扩张”时期却呈现“凹性皱眉” （concave frown）。这一原有文献中没有过的有趣发现，再次印证VIX期权的“事前定价”有独特的、不同于SPX期权之处。

论文理论部分建立了一个基于禀赋的一般均衡模型来解释上述发现。类似［班萨尔—亚伦2004（Bansal-Yaron 2004）］模型，消费禀赋有时变的波动率。波动率随机地向上跳跃，跳跃有时变的发生概率。因此，此模型是一个双因子模型——“波动率”和跳跃的“波动率的波动率”。在均衡中，消费禀赋的双因子传导成股票指数的双因子，继而传导成VIX指数的双因子。任一因子上升时，VIX指数上升，同时通过贴现率的上升使SPX下降。因此，论文作者把双因子称为“贴现率因子”。除此之外，论文作者把消费禀赋理解为第三个因子——“现金流因子”。

该模型内生了股票指数、VIX指数、SPX期权、VIX期货和VIX期权的价格。该模型有“低波动率（扩张）”时期和“高波动率（衰退）”時期。扩张时期，现金流风险更重要。因为在均衡里VIX指数只反映了股票指数分布的高阶矩，VIX不受现金流风险的影响。现金流风险因此只影响SPX期权而不影响VIX期货或期权。因此，扩张时期，SPX期权和VIX期权之间关系微弱，VIX期权几乎不能帮助对冲SPX期权。衰退时期（也即是波动率因而贴现率变动很大的时期），贴现率风险更重要。贴现率风险既影响VIX期货和VIX期权，也影响SPX期权。因此，衰退时期，SPX期权和VIX期权之间关系紧密，VIX期权能很好地对冲SPX期权。即使论文作者在对冲回归里控制了VIX期货，这仍不足以消除VIX期权的作用。这是因为期权价格是波动率因子的“凸函数”，而VIX期货几乎是波动率因子的“线性函数”，控制VIX期货不足以控制期权的“凸性”（convexity）。该模型因此解释了对冲回归的结果。

该模型还解释了VIX期权隐含波动率曲线随经济周期的变化。低波动率时期，VIX的向上跳跃风险更重要，因此隐含波动率曲线向上倾斜，并且呈现“凹性皱眉”。高波动率时期，VIX的向下扩散（diffusion）风险更重要，因此隐含波动率曲线向下倾斜或比较平坦，并且呈现“凸性微笑”。这和论文作者在数据中观察到的十分相似。

该模型在参数校准（将消费和股利数据进行了匹配）之后不仅能解释VIX、SPX衍生品数据，还同时能解释很多传统的资产定价谜题，例如股权溢价、低无风险利率、方差风险溢价、短期股权回报可预测性等。原有文献中现有的一般均衡资产定价模型（长期风险、罕见灾难、习惯等）也能解决这些谜题，但不能解释VIX期权的价格或VIX、SPX期权的关系。因此，论文作者的模型代表了这类一般均衡资产定价模型文献的前沿。

该模型还有额外的技术贡献。例如揭示了“递归偏好”和“双因子”在解释VIX衍生品价格时的必要性。前者是因为，在一般均衡里，VIX指数只能是消费禀赋分布高阶矩的函数。要使VIX指数有非零的“风险价格”，消费禀赋的高阶矩必须有非零的“风险价格”。其必要条件便是投资者有“递归偏好” （recursive preferences）。后者是因为，单因子模型必然导致VIX期权和VIX之间的相关性为100%，这与数据不符。也必然不能解释VIX期权隐含波动率的时变。此外，在该模型和文献中，方差（variance）都被假设遵循仿射过程。而VIX是衡量波动率的指标（volatility measure），从方差到波动率有一个平方根转换，这给推导VIX期权的定价公式增添了额外困难，克服这一技术困难不仅是论文的贡献，而且对于解释VIX期权隐含波动率曲线大部分时间呈现“凹性皱眉”是必要的。

原有文献里已经有一些VIX衍生品定价模型，但是这些模型几乎全是简化形式的模型，不能回答三个经济学问题：第一，VIX期权为什么“不多余”？第二，VIX衍生品价格能揭示投资者的偏好吗？第三，VIX衍生品价格和消费、股利数据存在内在冲突吗？论文填补了这些文献空缺。

（杨翱翔为北京大学汇丰商学院助理教授。原论文《高阶灾难保险的价格：VIX期权的例子》（The Price of Higher Order Catastrophe Insurance： The Case of VIX Options）2022年12月刊发于《金融学期刊》（Journal of Finance）。本文编辑/孙世选）