传统SK型与新型静态混合器的结构优化

陈西锋 陈晔

摘 要：为了提高聚丙烯腈纤维的合成质量，从提高合成聚丙烯腈的三股物料混合均匀度出发，利用CFD技术进行多相流流场的数值计算方法，探讨SK型静态混合器的元件结构参数及元件数量对混合器管内三股物料预混均匀度的影响，并分析相应的压力降变化等。结果表明：当混合元件的宽度D=110 mm、长宽比L/D=1、元件扭转角α=270°时混合效率最高。为达到理想混合均匀度的目的，以优化后的混合元件参数为基础设计一种新型静态混合器并对其进行数值模拟，满足要求时的新型混合器的总长度约为传统SK型静态混合器长度的1/2。新型静态混合器的混合效率比传统SK型静态混合器约提高了50%，但压力降损失也较大。

关键词：静态混合器；聚丙烯腈纤维；混合均匀度；CFD技术；多相流

中图分类号：TH122;TQ021.1

文献标志码：A

文章编号：1009-265X（2023）03-0001-11

基金项目：中石化安庆分公司技术开发（委托）项目（32000000-21-ZC0607-0006）

作者简介：陈西锋（1995—），男，安徽阜阳人，硕士研究生，主要从事流体仿真方面的研究。

通信作者：陈晔，E-mail：chenye@njtech.edu.cn

随着现代有机合成工业技术的发展，中国的腈纶合成技术也在逐步提高［1］。聚丙烯腈纤维可以用来代替羊毛，或与羊毛混纺制成毛织物等，是重要的纺织原材料。其用途十分广泛，它不仅用于日常生活中也用于军事中［2-3］。随着人们生活水平的提高，提高聚丙烯腈的合成质量也迫在眉睫。目前，聚丙烯腈的合成主要在聚合釜内完成，其合成的原材料通过不同进料管输入釜内，为了提高釜内聚丙烯腈的合成质量就必须引入一个新型进料系统（一种静态混合器），使3种单体在进入聚合釜前已达到充分混合。

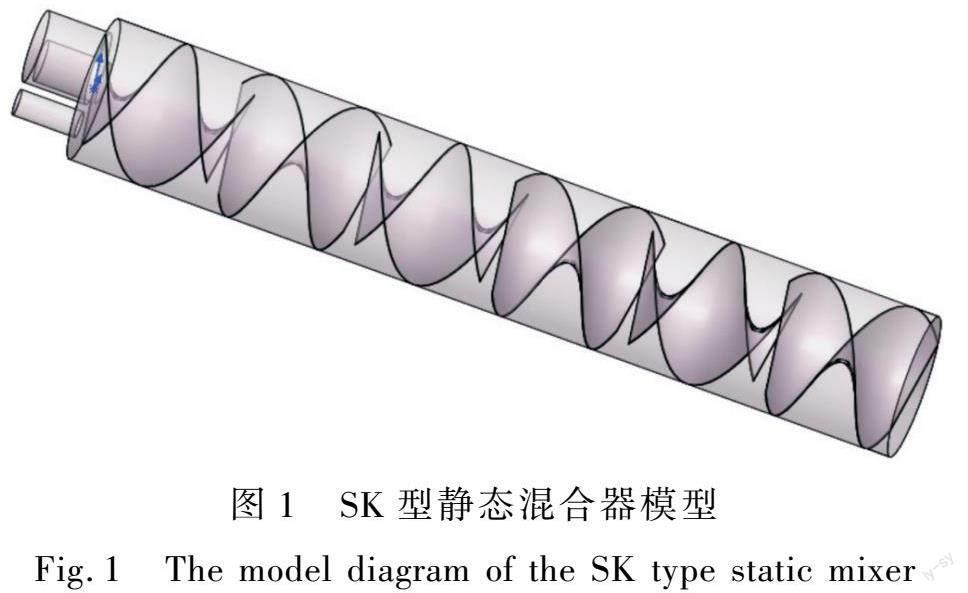
目前用于液-液混合的静态混合器主要有5种［4-5］，分别是SV型、SX型、SL型、SH型、SK型。不同的静态混合器有着不同的特点，其中SK型静态混合器混合效率较低于其他静态混合器，但其结构简单、易于制造、经济实用、便于维修、压力降损失较小等优点，在工业生产中被广泛使用［6］。目前许多学者对SK型静态混合器进行了大量的研究，龚斌等［7］研究了混合元件长径比对混合器湍流流场的影响，研究表明长径比的减小将引起各方向流速波动加剧，流体的湍动程度增加，长径比由2降为1时湍动能幅值约增加了4倍。Jiang等［8］研究了元件厚度对SK型静态混合器压降的影响，通过在牛顿流体及管内流动状态为湍流的条件下得到了摩擦系數与雷诺数、元件长宽比、自由截面积比的关系式，而自由截面积比与元件厚度有关，根据表达式从而得到元件厚度对静态混合器压降有较大的影响。Nyande等［9］对层流条件下低压降SK型静态混合器进行CFD分析，研究结果表明当SK型静态混合器的相邻混合元件的旋向不同且无间隙时，达到混合均匀度时的管道长度最短，然而当混合元件有间隙时其压力降大大减小，但管道长度也相应地增加。Towoju等［10］用开槽的混合元件对不同流体进行混合，研究结果表明当槽宽为0.2 mm且个数为2时混合效果达到最佳。Obed等［11］对SK型静态混合器管道内湍流强化传热进行研究，研究表明SK型静态混合器显著提高了管内的传热速率，摩擦系数也相应增加。龚斌等［12］对混合元件个数对SK型静态混合器流场特性的影响进行了研究，结果表明在前3个混合元件中湍动强化呈递减趋势，即湍动逐渐增加，但增加速度逐渐减弱。考虑到SK型结构简单及压力降损失小等特点，本文将在SK型静态混合器的基础上研究出一种新型的静态混合器，并确定其相关的参数，以提高三股物料的预混效率。SK型静态混合器是由一个管道及若干混合元件组合而成，其中混合元件有一定的扭转角，相邻元件间的偏转角为90°［13］，其混合原理是流体经过混合器时被内部混合单元不断切割，又由于混合元件具有一定的扭转角度迫使流体方向不断进行改变，产生对流和涡旋的运动，被分割的流体又会在两个单元间相交汇，如此重复运动使得流体混合均匀，这就是SK型静态混合器的工作原理。如图1为SK型静态混合器模型图。

物料的运输是在室温下（18℃）进行的，由于室温的温度较低并且与各相流体的温度相差不大，因此室温对各相流体的温度影响较小，通常可以忽略，又由于各相物料温度在30℃以下时发生聚合反应较少，综合以上可以忽略室温对物料本身温度、密度及黏度的影响，因此可以把各相流体看成各不相同的均质流体，为其流场数值模拟提供了可行性。随着计算流体力学技术（CFD）不断成熟，为新型静态混合器的结构优化提供了技术基础［14-15］。

1 SK型静态混合器相关结构参数优化

1.1 三股物料的组成及其相关性质

表1为各相物料的组成及其相关性质。第一相流体为丙烯腈单体，第二相流体较为特殊，它是由丙烯腈单体、醋酸乙烯酯单体及水组合而成的，第三相流体为醋酸乙烯酯单体。由于各相流体的温度较为特殊，所以不同流体对应的黏度及密度数值无法直接获取，而是通过密度计及流变仪进行现场实验而获得的。

1.2 混合器管径的确定及进料管的相关尺寸和位置

通过三根进料管分别输送三相流体至静态混合器，由于进料流量不大，相应地第一、二、三相流体的进料管直径d1、d2、d3的值也不大，其值可以合理地确定，各进料管圆心到静态混合器的圆心距离分别为l1、l2、l3，进料管长度为l0，各进料管圆心与混合器圆心间的夹角为120°，其相关的数据如表2所示。

1.3 计算域构建及网格划分

由于该计算模型较为简单，所以流体域可以直接在Design Modeler模块上建立，先建立总的圆柱体流体域，然后通过Sweep操作建立混合元件，利用Boolen功能将圆柱体流体域作为目标体而混合元件作为刀具进行布尔操作，最终得到流体域，此流体域不需要简化因此更能反应真实性，考虑到流体域的不规性，不能用六面体网格对流体域进行划分，于是选用四面体网格。网格划分完成需要检查网格质量，主要包括网格质量、歪斜率、正交质量［16］，其中网格质量和正交质量均要大于0.95而歪斜率则要小于0.25，避免因网格质量问题而造成的模拟误差。

以下是对单混合元件静态混合器进行网格无关性验证，如图2所示。从图2中可以看出，当计算区域的网格总数N由74842增大到134213时，进料管1的入口压力基本保持不变，这说明当网格数为74842时，网格精度已经达到了计算所需要的要求。因此，将具有74842个网格数的模型用于单单元静态混合器的数值模拟。由于本文所研究的模型较多，后续不同模型的网格数均由此方法确定。

1.4 多相流模型的选取及边界条件的设置

当前研究多相流的方法有欧拉-拉格朗日方法和欧拉-欧拉方法［17］，在Fluent中一共有以下3个欧拉-欧拉多相流模型，他们是VOF模型，混合模型，欧拉模型；其中VOF模型可以得到一种或多种互不相融流体间的交界面，而Mixture模型则是相对简化了的模型，相较于其他模型具有计算量较小的特点，欧拉模型是流体中最复杂的多相流模型，其计算结果较为准确，但其计算的稳定性较差。本文则选取Mixture模型进行数值模拟计算。

边界条件选择速度入口，根据1.1中各进料管的大小及各相流体的流量，通过计算可得第一、二、三相流体的进料流速v1、v2、v3分别为0.3、0.2、0.2 m/s，出口边界条件设置成压力出口，壁面定义为固定壁面，且满足无滑移的条件。

1.5 SK型静态混合器单单元结构相关参数对混合均匀度的影响

1.5.1 静态混合器管径大小对物料混合均匀度的影响

SK型静态混合器混合单元的主要结构参数有3种，即元件的宽度（混合元件的宽度与混合器内径相等）、元件的长宽比及元件的扭转角，本文所采用混合元件的厚度均为2 mm。由于各相流体的黏度都较低，为了能获得较高的混合效率所以本文选择流体流动状态为湍流，而管内流体流动状态是否为湍流则取决于管径大小d及混合器管入口表观流速v所决定的，湍流的判别方法用雷诺数Re判断，当Re>4000时为湍流状态，其表达式如式（1）［18］：

式中：ρ代表流体的密度；d代表混合器圆管的直径；v代表流体的表观流速；η则代表流体的黏度。

根据式（1），在满足混合器内混合状态为湍流的条件下，分别选取4种不同的混合器管内径D1=110 mm，D2=126 mm，D3=142 mm，D4=150 mm，采用控制变量的方法，控制混合器长径比L/D=1，混合元件单元扭转角度α=180°，分别建立对应的流体域后进行数值模拟计算。

由于是对单单元静态混合器进行数值模拟，其混合均匀度较差，很难用一种评价指标来判断混合效率，所以本文将会从多个方面综合评价其混合均匀度。第一种评价指标为出口截面处各相体积分数数值与理论混合均匀度的各相体积分数数值之间的偏差，第二种评价指标为出口处截面平均密度值的变化，第三种评价指标为观察静态混合器出口截面处各相体积分数分布云图。如不能通过其中一种指标判断，则需要通过多种指标综合比较，可以更为准确地判断流体的混合效率。如图3为不同管径下的SK型静态混合器出口截面处各相体积分数平均值及各相混合均匀时的理论值线图，图4为不同管径下的SK型静态混合器出口截面处第一相体积分数分布云图。从图3可以明显地看出当管径大小为150 mm时，其各相体积分数平均值与其理论值偏差最大，表明了其混合效率最差，而其他3个不同管径大小对混合效率的影响从图3很难判断。结合图4比较第一相流体体积分数大于0.9的面积大小，其面积越大表明混合效率越差，从图4中可以明显地观察到第一相流体体积分数大于0.9的面积随着管径的增大而增大，表明其混合效率逐渐变差，又由于第一相流体的密度明显低于其他两相，则混合器出口横截面平均流体密度将逐渐减小，这也符合图5中混合器出口截面平均密度随着混合器管径的增加而逐渐减小的规律。综合比较两图可得到當混合器的管径增大时，对应的混合效率下降。

1.5.2 静态混合器元件长宽比对物料混合均匀度的影响

分别选取常用的SK型静态混合器混合元件长宽比L/D（即混合单元元件的长度与其宽度之比）为1.0、1.3、1.5。其中混合器的内径d选取110 mm，单元扭转角度α取180°，建立相对应的流体域后分别进行数值模拟计算。同理从图6中明显看出各相体积分数平均值与理论平均值偏差最大，表明当L/D=1.5时其混合效率最差，从图7中也只能明显地判断出当L/D=1.5时其混合效率最差且不能判断出其他两个长宽比对混合效率的影响，因此需要增加元件的数量，当元件的数量为3个时，比较出口处第一相体积分数分布云图，由图8可以明显地看出当混合元件长宽比为1时要大于长宽比为1.3时的混合效率。由于元件长宽比的减小将引起各方向流速波动加剧，当流体的湍动程度增加［8］，有利于流体的混合。所以混合器元件长宽比的减小将提高流体的混合效率。综合以上，当混合元件长宽比增加时，其混合效率随之降低。

1.5.3 静态混合器元件扭转角α对物料混合均匀度的影响

元件的扭转角即为一平板件的底边相对于顶边所扭转过的角度，根据旋向的不同可以分为左旋和右旋，如图9所示为不同扭转角的混合元件。为了探究混合元件扭转角α对混合效率的影响，分别选取常用的扭转角α=90°、α=180°、α=270°，通过分别进行数值模拟试验，探讨不同单元扭转角度对混合器的混合效率的影响。根据图10可以看出当扭转角增大时，第一相体积分数值大于0.9的面积逐渐减少，表明混合效率逐渐提高。综合以上，当混合元件扭转角α增大时，其混合效率也在变大。

1.6 混合元件相关参数的优化

根据上述的单因素试验的研究及结论，采用正交实验的方法对混合元件相关尺寸进行优化，正交试验探讨的影响因素为混合器管径、混合元件长宽比、混合元件扭转角。因素水平编码如表3所示。

利用Design-Expert软件设计正交试验表并进行仿真模拟试验，以各影响因素取值为自变量，以混合器出口处截面各相体积分数平均值为评价指标。正交试验结果如表4所示，以单单元静态混合器出口截面处第一相平均体积分数值0.76760000、第二相平均体积分数值0.16710000、第三相平均体积分数值006527000为目标（数值分别为第一、二、三相体积分数理论值）利用软件Design-Expert中Optimization-Numerical-Solutions得到相对应的最佳单元尺寸，其中混合器直径为110 mm，混合元件长宽比为1，元件扭转角为270°。与单因素试验中得到的最优尺寸值一致。

1.7 混合元件个数的确定

由于SK型静态混合器第一个混合元件对整个混合器的混合效率影响甚大，而第一个混合元件的相关参数已经确定，所以静态混合器的其他混合元件的参数选择与第一个混合元件的参数保持一致。为了提高元件的混合效率，使相邻元件的扭转角度相同但旋向不同，并且相邻元件间的偏转角为90°。分别取混合元件个数n=4、5、6进行数值模拟，提取混合器截面出口处各相体积分数云图，如图11所示（从左至右分别为一、二、三相积分数云图）。

从图11中可以明显地发现流体的混合均匀度随着元件个数的增加而提高，当混合元件个数为6时，流体混合已较为均匀，当n=6时，分别随机选取10个点，提取每个点的第1、2、3相体积分数，如图12为不同随机点的各相体积分数数值对应的点线图。从图12中可以看出不同随机点对应同一相的体积分数数值变化不大，都在理论值附近，证明混合效果较好，通过计算得到第一、二、三相体积分数值与理论值最大偏差仅为0.18%、180%、370%，最大偏差值都小于5%，表明混合均匀度已经达到期望，此时混合器的长度为660 mm。图13为不同混合元件个数的进出口压力降线图，从图13中可以看出随着混合元件个数的增加，其进出口压力降也增大，这表明增加混合元件的个数也增加了能量的消耗。

2 新型靜态混合器结构参数的确定

2.1 新型静态混合器模型简介

秉承着结构简单的设计原则，新型静态混合器由SK型静态混合器改进而成的，其模型图如图14所示，其中第一部分是传统SK型静态混合器单单元结构部分，与1.6节所确定的单单元静态混合器相关尺寸一致。第二部分为直径为110 mm高为10 mm且底部设有倒直角的形体（两边的倒角距离都为10 mm），这一部分主要是自由混合区域，流体在离开第一个混合元件时利用动能进行自由混合，开有倒角是为了增加横向混合动能，使得混合更加充分。第三部分是连接自由混合区域的混合器，根据上文可知混合器管径较小时有利于混合，所以此部分的混合元件的宽度选取为44 mm，使其明显小于第一个混合元件的宽度。为保证混合效率，长宽比和元件扭转角与上文优化结果一致，相邻元件的偏转角为90°并且元件的旋向各不相同。

2.2 数值模拟结果及分析

2.2.1 混合元件个数的确定

混合元件个数的确定方法与上文一致，分别取混合元件个数为4、5时，提取不同混合元件个数下的各相体积分数分布云图，如图15所示。从图15中可以看出当混合元件个数为5时流体已达到混合均匀，同样分别在各相体积分数云图中随机选取10个点，提取不同点对应的各相体积分数数值，通过计算后得到各相体积分数与理论体积分数的偏差均小于5%，其混合均匀度已达到要求。如图16为新型静态混合器的轴截面湍动能云图，从图16中可以明显地发现在混合器管径较小的那一部分其湍动能较大，流体在此部分产生强烈的混合。如图17为不同混合元件个数对应的进出口压力降，结果表明新型静态混合器的压力降也随着混合元件的个数增加而增大，与传统SK型静态混合器相比其压力降较大，表明能耗损失较大，但其混合效率大大提高。新型静态混合器的总长度为340 mm，其长度约为SK型静态混合器的一半，大大地减少了混合器材料用量。无论是传统静态混合器还是新型静态混合器，伴随着混合效率提高的同时压力降的损失也在增大，但相比于其他类型的静态混合器其压力降损失是相对较小的。

2.2.2 具有较高混合效率的位置判断

为了进一步探究流体的高混合效率主要存在于哪部分，分别在自由混区底部及第二、三、四个混合元件底部设置横截面，依次提取各横截面处的流体速度矢量图，如图18所示。从流形可以看出，当流体经过自由混合区时，其混合效率并不高，但当流体经过第二个混合元件之后，流体的混合效率大大提高，从图18中第2部分可以看出大量的流体速度方向趋向于垂直混合器管壁，当流体碰到管壁时，其速度方向将会改变，因而能产生更强的混合反应。而当流体经过第三个混合元件底部时，流体的混合效率明显地降低，从图18中可以看出虽然存在两个有利于混合的小涡流，但从整体上流体接近于做周向旋转运动，减弱了混合效果。同理，当流体经过第四个混合元件底部时，其混合效率更低。根据以上可以知道流体在经过第二、三个混合元件时，流体具有较高的混合效率，但此时并未达到要求的混合均匀度，要想达到混合均匀度就需要再增加混合元件来达到目的。

3 结 论

本文首先对SK型静态混合器单单元结构进行优化，确定了最优单元宽度D（等于混合器管径）、元件长宽比L/D、元件扭转角α，并确定了混合元件的数量，在此基础上确定了新型静态混合器的相关参数，得到的主要结论如下：

a）SK型静态混合器单单元最优尺寸中单元宽度D=110 mm、元件长宽比L/D=1、元件扭转角α=270°，随着混合元件的个数增加，其混合均匀度也在增加但压力降也在增加，流体达到理想混合均匀度时的元件个数n=6。

b）新型静态混合器相比于传统SK型静态混合器有较高的混合效率，达到理想混合均匀度时的混合器总长度约为SK型静态混合器的1/2，大大节省了材料的利用。新型静态混合器内管内直径较小的部分其湍动能较大，有利于流体的混合但压力降损失较大，增加了能量的消耗。

参考文献：

［1］李青山，沈新元.腈纶生产工学［M］.北京：中国纺织出版社，2000.

LI Qingshan， SHEN Xinyuan. Acrylic Production Enginee-ring［M］. Beijing： China Textile Publishing House， 2000.

［2］康鲁浩，王成国，井敏，等.碳纤维用聚丙烯腈合成工艺研究进展［J］.能源化工，2015，36（1）：67-72.

KANG Luhao， WANG Chengguo， JING Min， et al. Research progress on polyacrylonitrile synthesis process for carbon fiber［J］. Energy Chemical Industry， 2015， 36（1）： 67-72.

［3］贺福，赵建国，王润娥.碳纤维工业的长足发展［J］.高科技纤维与应用，2000，25（4）：9-13.

HE Fu， ZHAO Jianguo， WANG Run'e. The rapid develop-ment of the carbon fiber industry［J］. Hi-Tech Fiber and Application， 2000， 25（4）： 9-13.

［4］吴德荣.化工装置工艺设计［M］.上海：华东理工大学出版社，2014.

WU Derong. Process Design of Chemical Plants［M］. Shanghai： East China University of Science and Technology Press， 2014.

［5］吴英桦.粘性流体混合及设备［M］.北京：中国轻工业出版社，1993.

WU Yinghua. Viscous Fluid Mixing and Equipment［M］. Beijing： China Light Industry Press， 1993.

［6］姬宜朋.旋转式Kenics型混合器混合性能及流动特性研究［D］.北京：北京化工大学，2005.

JI Yipeng. Study on Mixing Performance and Flow Characteristics of Rotary Kenics Mixer［D］. Beijing： Beijing University of Chemical Technology， 2005.

［7］龚斌，包忠平，黄娜，等.元件长径比对SK型静态混合器湍流流场的影响［J］.石油化工高等学校学报，2009，22（1）：65-68.

GONG Bin， BAO Zhongping， HUANG Na， et al. The effect of component length-to-diameter ratio on the turbulent flow field of SK type static mixers［J］. Journal of Petrochemical Universities， 2009， 22（1）： 65-68.

［8］JIANG X G， XIAO Z D， JIANG J A， et al. Effect of element thickness on the pressure drop in the Kenics static mixer［J］. Chemical Engineering Journal，2021，424.

［9］NYANDE B W， MATHEW T K， RICHARD L. CFD analysis of a kenics static mixer with a low pressure drop under laminar flow conditions［J］. Industrial & Engineering Chemistry Research， 2021， 60（14）： 5264-5277.

［10］TOWOJU O A， ISHOLA F A. Performance characte-rization of a kenics static mixer using slotted elements［J］. IOP Conference Series： Materials Science and Engineering， 2021， 1107（1）： 1-8.

［11］OBED Y W A， JKIZITO J P. Turbulent heat transfer enhancement in an axially rotating pipe fitted with kenics segment mixer［J］. Results in Engineering， 2020， 7： 1-7.

［12］龚斌，包忠平，张春梅，等.混合元件数对SK型静态混合器流场特性的影响［J］.化工学报，2009，60（8）：1974-1980.

GONG Bin， BAO Zhongping， ZHANG Chunmei， et al. The influence of the number of mixing elements on the flow field characteristics of the SK type static mixer［J］. CIESC Journal， 2009， 60（8）： 1974-1980.

［13］裴凱凯.SK型静态混合器摩阻系数与混合效果的模拟研究［J］.化工与医药工程，2021，42（2）：7-13.

PEI Kaikai. Simulation study on friction coefficient and mixing effect of SK type static mixer［J］. Chemical and Pharmaceutical Engineering， 2021， 42（2）： 7-13.

［14］张春梅.SK型静态混合器流动特性研究［D］.天津：天津大学，2009.

ZHANG Chunmei. Study on the Flow Characteristics of SK Type Static Mixer［D］. Tianjin： Tianjin University， 2009.

［15］朱紅钧.流体分析及工程仿真［M］.北京：清华大学出版社，2011.

ZHU Hongjun. Fluid Analysis and Engineering Simulation［M］. Beijing： Tsinghua University Press， 2011.

［16］胡坤.计算流体力学基础及应用［M］.北京：机械工业出版社，2019.

HU Kun. Computational Fluid Dynamics Fundamentals and Applications［M］. Beijing： Mechanical Industry Press， 2019.

［17］王瑞金.Fluent技术基础及应用实例［M］.北京：清华大学出版社，2007.

WANG Ruijin. Fluent Technology Basics and Application Examples［M］. Beijing： Tsinghua University Press， 2007.

［18］吴平，邱红梅，徐美.当代大学物理［M］.北京：机械工业出版社，2020.

WU Ping， QIU Hongmei， XU Mei. Contemporary Univer-sity Physics［M］. Beijing： Mechanical Industry Press， 2020.

Abstract： China's demand for polyacrylonitrile fibers is increasing year by year， so the synthetic quality of polyacrylonitrile is also increasingly high. The synthesis process of polyacrylonitrile is made of three different materials through three feed pipes into the polymerization kettle for polymerization reaction. In the production process， "scarring" and poor molecular quality of polyacrylonitrile often occur at the bottom of the feed pipe. The reason for the formation of "scarring" phenomenon is that when the temperature of the monomer near the bottom of the feed pipe rises suddenly in the process of pipeline transportation， more self-polymerization reactions occur on the monomer， and the self-polymerization products will be attached to the bottom of the pipe. Over timem the "scarring" phenomenon appears at the bottom of the feed pipe， which will lead to the blocking of the bottom of the feed pipe in serious cases， resulting in great economic losses. Due to the polymerization of the three strands before entering the polymerization kettle， the synthesis quality of polyacrylonitrile will be poor.

In order to improve the synthetic quality of polyacrylonitrile fibers， the feeding system will be redesigned. In order to improve the mixing uniformity of three strands of polyacrylonitrile， a static mixer of SK type was introduced into the feeding system. The numerical calculation method of multiphase flow field was carried out by CFD technology. The influence of relevant structural parameters of the elements of SK type static mixer and the number of elements on the premixed uniformity of three strands of materials in the mixer tube was discussed， and the corresponding pressure drop was analyzed. The related dimensions of the optimal mixing effect of the mixing elements were obtained by orthogonal test. A new static mixer was designed based on the optimized parameters of the mixing elements for the purpose of achieving the ideal mixing uniformity. The new static mixer was mainly composed of two sections with different diameters. It is found that the mixing efficiency is the best when the width D is 110， the aspect ratio L/D is 1， and the torsion angle of the component α is 270°， and the ideal mixing uniformity is reached when the number of elements N is equal to 6. In the new static mixer， the size of the first mixing element is optimized， the width of the mixing element D in the 44mm pipe section is 44mm， and other parameters are unchanged. After numerical calculation and analysis， when the number of mixing elements is 5， the mixing uniformity of the fluid reaches the ideal value. The total length of the designed new static mixer is about 1/2 of the length of the traditional SK type static mixer， and the mixing efficiency is also about 50% higher. However， with the improvement of the mixing efficiency， the pressure drop at the inlet and outlet of the mixer is significantly increased， and the pressure drop loss is increased.

Both the traditional static mixer and the new static mixer can fully mix the materials. The difference is that when the traditional static mixer reaches the mixing uniformity， its length is longer and the pressure drop is smaller， while the new static mixer has shorter length and the pressure drop is larger. The new static mixer can be used in situations where the length of the mixer is required but the pressure drop is not high. The research results provide reference for the design and development of static mixer.

Keywords： static mixer; polyacrylonitrile fiber; mixing uniformity; CFD technology; multiphase flow; pressure drop