基于机器学习的多模型耦合径流预报研究

2023-05-26祝宾皓张勇传

中国农村水利水电 2023年5期

祝宾皓，，方威，张勇传

（1.华中科技大学土木与水利工程学院，湖北武汉 430074；2.华中科技大学数字流域科学与技术湖北省重点实验室，湖北武汉 430074）

0 引言

洪水预报作为一种有效的防洪非工程措施，在防洪减灾紧急决策中发挥着不可替代的作用。洪水预报相关理论方法，经历了由经验模型到具有系统理论概念的黑箱模型，再到结合物理过程和经验概化的概念性水文模型，最后到反映流域空间分异性的分布式水文模型的发展过程［1］。然而任何一类水文模型都是对水循环过程选择性概化的近似描述，理论上无法精确还原真实水文过程。另外，在洪水预报中难以避免地存在降雨输入、模型结构以及参数的不确定性问题，前述不确定性的存在必将导致洪水预报结果的不确定性，因此探索一种强鲁棒性、高精度的洪水预报模式已成为亟待解决的问题。

自19世纪40年代起，众多水文工作者已开展关于水文不确定性对洪水预报的影响研究，其中，考虑降雨输入、参数不确定性影响的研究聚焦于对误差概率分布特征的定量刻画；考虑模型结构不确定性影响的研究聚焦于模型产汇流机理的改进以及预报模型优选策略、模型耦合预报等方面。KRZYSZTO‐FOWICZ［2］提出贝叶斯洪水预报理论，应用降雨不确定性处理机（Precipitation Uncertainty Processor， PUP）和水文不确定性处理机（Hydrologic Uncertainty Processor， HUP）分别处理降雨输入不确定性和降雨以外的其他不确定性，从而明确洪水预报的总不确定性；KAVETSKI等［3］采用额外隐变量降低降雨输入的不确定性，提出了贝叶斯总偏差分析（BayesianTotal Error Analy‐sis， BTEA）方法；AJAMI等［4］通过改用折算系数映射降雨输入的不确定性，并结合贝叶斯模型平均（Bayesian Model Averag‐ing， BMA）方法考虑模型结构不确定性，提出了贝叶斯综合不确定性估计方法（the Integrated Bayesian Uncertainty Estimator，IBUNE）；谢小燕［5］将多元门限回归模型和（Artificial Neural Net‐work， ANN）模型进行耦合预报，完成了小山水库的中长期水文预报；冯钧等［6］将（Back Propagation， BP）网络和（Long Short-Term Memory， LSTM）模型在子午河流域进行耦合预报，发现预报结果优于任一单模型的预报结果；丁武等［7］采用极端梯度提升树法（eXtreme Gradient Boosting， XGBoost）进行多元水文时间序列趋势相似性挖掘，达到了预测水文趋势的目的。

为降低模型结构不确定性对洪水预报带来的负面影响，拟探明各水文模型的预报特征，采用多祌水文模型的不同耦合策略构建洪水耦合预报系统，以探寻研究流域产汇流机理的精细化表达，降低极端降水事件所带来的影响。

1 多模型耦合方法

1.1 多模型耦合预报概述

水文预报是对未知水文情势的预测，无论选用什么水文模型都会有预报误差。但考虑到各个水文模型建模机制不同，在同一研究流域的预报表现也各不相同，拟综合多个模型的预报特征对研究流域的径流序列进行耦合预报。耦合预报定义如下：

式中：F为最终耦合预报径流预测值；wi为各模型被分配的权重，可以是显式的也可以是隐式的；fi是第i个水文模型预测值；h为水文模型个数。

1.2 单个预报模型的建立

为探明研究流域的产汇流机制，综合考虑影响预报结果的各种可能因素，本研究选择基于蓄满产流理念的新安江模型［8］、适用性较强的水箱模型［9］以及基于变动产流面积原理的TOP‐MODEL模型［10］，将3个模型的预测结果作为耦合模型的输入，经各耦合方法确定模型权重后，可由式（1）确定耦合预报的径流预测序列。由于（Particle Swarm Optimization， PSO）［11］算法已经广泛应用于水文模型的参数率定中［12-14］，故本研究各模型的参数以确定性系数（Determination Coefficient， DC）为目标函数，由PSO算法率定得到。确定性系数的计算如下所示：

式中：Q代表实测径流序列，代表实测径流序列的平均值代表预报径流序列；n代表序列长度。

1.3 最小二乘法

最小二乘法是一种数学方法，它通过寻求最小误差平方和的方式找到一组数据的最优函数形式，已经在参数估计、系统辨识以及预测等专业领域中得到广泛的应用。周建中等［15］提供了最小二乘法在水文模型耦合预报中的应用细节。

1.4 岭回归法

由于前述最小二乘法在处理本文的耦合预报时容易出现结果不稳定的缺陷，故引入岭回归法［16］进行耦合预报。岭回归法是一种适用于多重共线性数据分析的有偏估计回归方法，可视为改进的最小二乘法。该方法放弃最小二乘估计的无偏性，以损失部分信息、降低一定精度的代价获得更符合现实的回归系数［17］。本文的多模型耦合预报研究可归类为多重共线性问题，采用岭回归法可以更有力的挖掘多模型预报的优势，为研究流域的水文预报提供可靠保障。

1.5 极端梯度提升树法

极端梯度提升树，即XGBoost方法［18］在原始（Gradient Boosting Decision Tree， GBDT）模型的基础上进行了改造，以二阶泰勒展开方式代替GBDT模型中损失函数的一阶泰勒展开方式，增加了模型的泛化能力和对多维度数据间复杂关联的捕捉能力，该模型把正则化向的结构损失函数加入目标函数，以避免过拟合现象的发生，进一步提升了模型适用能力。本文将XGBoost算法应用于多模型耦合预报，有望精准捕捉各模型的预报特征并据此对该流域的径流序列做出符合实际的预报方案。XGBoost方法的基本原理如下：

已知某样本集

式中：xi为样本输入值；Xti、Yti、Zti分别为新安江模型、水箱模型和TOPMODEL模型在时刻i的预测值；n为径流序列长度；yi是样本输入值xi对应的输出值。

综合Mulligan的研究，我们探讨出许多问题。其一，对于Mulligan技术操作方便，效果显著，但是机制不明确；其二，研究探讨某种疾病或功能障碍时，无法给出明确纳入标准，禁忌症与适应证无明确的指南，只是通过疾病的适应症与禁忌症大体估量；其三，样本量和局限性的问题仍不能解决。目前国内与国外的差距明显。从研究内容上，国外Folk[47]的研究已经进展到手指关节，国内还没有研究到小关节；从研究文献的数量上，国外的研究也是领先于国内；从研究领域上，Kim[48]对脑卒中患者步态功能的恢复，应用动态松动术进行研究。

那么XGBoost模型的目标函数可以表示为：

式中：Fm代表模型在第m次迭代学习中的目标函数；式中第一项为损失函数项为第i个样本在第m-1次迭代学习中的预测值，fm(xi)为第m轮迭代学习中新加入的树基于输入值xi和上一次迭代学习误差做出的预测值；式中为正则化项，是对于模型复杂度的惩罚函数，T为叶子结点个数，ω为叶子权重向量，γ和λ为权重系数。

为使目标函数值最小，XGBoost方法需要评估所有叶子节点，挑选能使目标函数值最小的叶子节点进行分裂，评估函数如下：

最终叶子节点分裂完成且所有决策树的添加也完成时，各模型预测结果与耦合预报结果的隐特征关系就存储在XGBoost模型的结构中，再次调用训练过的XGBoost模型就可计算耦合预报结果。

2 应用实例

2.1 研究区域概况及数据集构造

雅砻江流域位于青藏高原东侧，四川西部，全长1 571 km，流域面积13.6万km2，干流狭长，支流呈树枝状均匀分布于干流两岸；河源至河口天然落差3 830 m，上游呈高山及高原景观，径流补给以冰雪为主，中下游为高原、高山峡谷河流，径流补给以降水为主，地势自西北向东南渐趋平缓；流域干湿季节明显，暴雨一般出现在6-9月，呈连续性、大范围、高强度的特点；全年径流量丰沛稳定，且空间异质性明显。

因雅江～吉居区间处于雅砻江流域中游和下游的分界处，径流受融雪、降水、地形各因素的影响程度不明确，故本文将其作为研究区域。研究中耦合预报采用的数据集由3 h尺度的新安江模型、水箱模型、TOPMODEL模型径流预报数据以及雅砻江流域雅江、吉居站点实测径流序列构成。其中各模型径流预报数据是本文基于雅砻江流域水电开发有限公司提供的雅江～吉居区间各气象站点3 h尺度的降水、蒸发、径流资料，以2005-2010年为率定期、2011-2013年为检验期，采用PSO算法确定模型参数后计算得到。研究流域图及水文、气象站点的空间分布信息见图1。

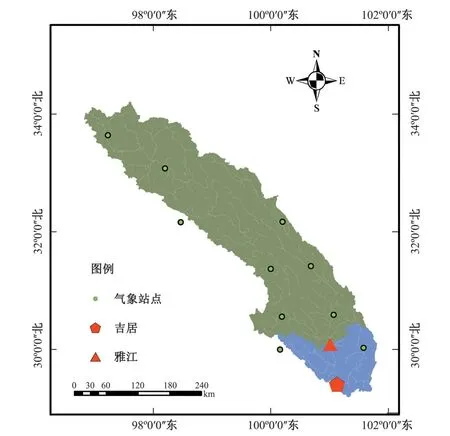
图1 研究区域气象站、流量站分布图Fig.1 Distribution diagram of meteorological stations and flow stations in the study area

2.2 模型性能评价指标

为了从多个角度全面、准确的评价本文采用的各种耦合预报方法，本文引入确定性系数DC、均方根误差（Root Mean Square Error，RMSE）和平均绝对误差（Mean Absolute Error，MAE）3个指标对模型的预报性能、预报稳定性进行评价。其中DC的计算由式（2）给出，RMSE和MAE的计算公式如下：

式中：Q代表实测径流序列̂代表预报径流序列；n代表序列长度。

2.3 应用实例结果分析

3个独立模型在3种耦合方法下的权重如表1、图2所示。

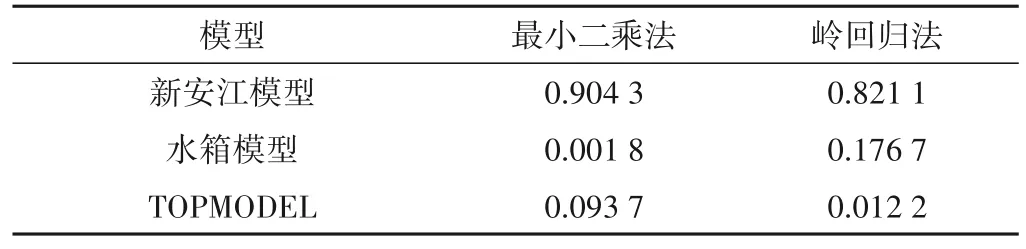
表1 各模型在两种回归方法中被赋予的权重Tab.1 The weights assigned to each model in two regression methods

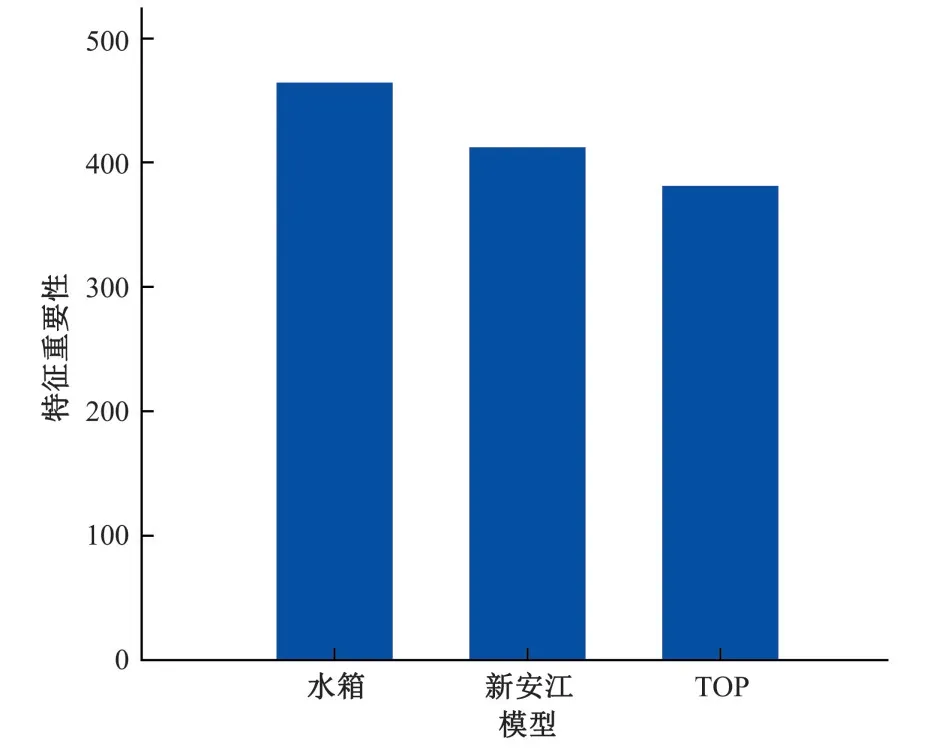
图2 各独立模型在XGBoost中的特征重要性Fig.2 Feature importance of each independent model in XGBoost

由表1可知，最小二乘法在赋予模型权重时，易受到模型间共线性的影响，从而赋予某个预报效果较好的模型过多的权重，这导致耦合预报失去了原本的意义；相较于最小二乘法，岭回归方法能提供一组更稳定、可解释性更强的模型权重；但以上两种回归方法都是直接将权重与预测序列相乘之后得到最终预测序列，这与综合考虑各模型预报特征进行耦合预报的初衷仍有出入。在XGBoost中，特征重要性是指节点分裂时该特征带来信息增益（目标函数）优化的平均值，特征对信息增益影响程度的大小决定了重要性的大小，且由图2可知各模型的预报特征在XGBoost的建模过程中得到了充分考虑，特征重要性并未出现过大的差距。结合图2中各模型的特征重要性以及各模型的建模原理（新安江模型侧重于蓄满产流，即土壤类型；水箱模型侧重于冰雪融水；TOPMODEL侧重于地形条件），可以认为对研究流域产汇流特征影响最大的因素是冰雪融水，其次是土壤类型和地形特征，这也与雅江～吉居区间地处青藏高原的地理位置相符合。

3个水文模型的预测表现以及3种耦合预报方法的预测表现如表2所示（加粗指标对应的模型为该评价指标下的最优模型）。

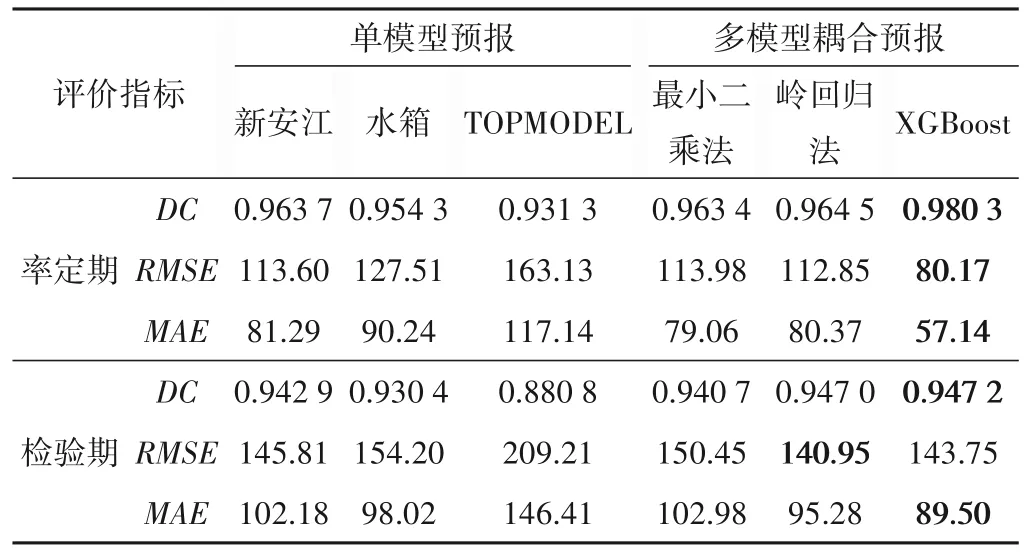
表2 模型输出结果Tab.2 Performances of all models

由表2、图3可知，独立模型的预报中，不同评价指标下的最优单个水文模型也是不同的，例如新安江模型在确定性系数、均方根误差这两个指标上的表现比其余两个水文模型好，但在检验期平均绝对误差的表现上不如水箱模型。所以没有任何一个水文模型能在所有评价指标上同时表现出最优。与此同时，在同一研究流域的不同预报阶段，同一水文模型的表现也会出现差异性，例如新安江模型在洪峰阶段的拟合效果较好，但在退水阶段，新安江模型就失去了拟合优势。这是因为天然水文过程自身具有极大的随机性和非线性特征，而各模型都是在某个侧重点上实现对水文过程的概化模拟，无法完全准确的模拟水文过程，所以单个模型的预测能力是有限的，目前不存在一个最优水文模型。

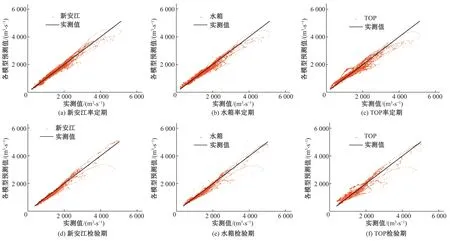
图3 独立模型预测结果Fig.3 Prediction results of independent model

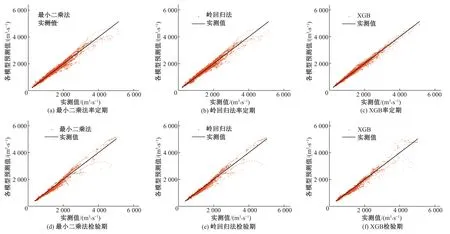
图4 耦合模型预测结果Fig.4 Prediction results of coupled model

由表2、图3、4可知，多模型耦合预报的预测表现普遍优于单模型预报，但基于最小二乘法的传统耦合预报在处理此类多重共线性问题时，效果劣于最优独立模型。针对此缺陷做出改进的岭回归法在预测表现以及适用性上都要强于最小二乘法，但在多数评价指标上的表现劣于XGBoost方法。多模型耦合预报中，在率定期的拟合效果方面，XGBoost方法相较于最小二乘法、岭回归法分别提升了1.69%、1.58%；在预测误差方面，以RMSE为指标，XGBoost方法相较于最小二乘法、岭回归法分别降低了29.66%、28.96%；以MAE为指标，XGBoost方法相较于最小二乘法、岭回归法分别降低了27.72%、28.90%。检验期内，在拟合效果方面，XGBoost方法相较于最小二乘法、岭回归法分别提升了0.65%、0.02%；在预测误差方面，以RMSE为指标，XGBoost方法相较于最小二乘法降低了4.45%、相较于岭回归法提升了1.99%；以MAE为指标，XGBoost方法相较于最小二乘法、岭回归法分别降低了13.09%、6.07%。

整体来看，3种耦合预报方法中，XGBoost方法预报效果最优、岭回归法次之、最小二乘法最差，且不同时期内XGBoost方法的预报效果未出现较大差异。充分证明XGBoost方法较其他方法能更深入地挖掘各模型在研究流域表现出的不同预报特征并据此进行耦合预报，同时展现出XGBoost方法良好的稳健性和强大的泛化能力。