基于萤火虫算法优化BP神经网络的爆破振速预测
2023-05-26张勇李旋尹燕良李富杰
张勇 李旋 尹燕良 李富杰


摘要:
爆破振动是岩体爆破开挖工程中典型的有害效应,实现爆破振动精准预测对爆破过程中的风险控制意义重大。为实现这一目标,借助萤火虫算法(FA)对反向传播神经网络(BPNN)的权值和阈值进行优化,构建FA-BP神经网络预测模型,以露天矿山台阶爆破中多个设计参数和爆心距为模型输入参数,对峰值质点振速进行预测,并比较FA-BP神经网络模型、统计预测方程、BPNN模型和随机森林方法的预测结果。最后,借助归一化互信息分析各输入参数对FA-BPNN预测结果的敏感性。研究结果表明:FA-BPNN模型能有效预测爆破峰值质点速度,预测结果对应的均方根误差、平均绝对误差和决定系数分别为1.445,1.182和0.973,预测效果较其余3种方法更好;单段最大装药量、爆心距、炸药单耗、台阶高度与抵抗线长度之比对爆破峰值振速预测结果影响较大。
关 键 词:
工程爆破; 爆破振动; 峰值振动速度; BP神经网络; 萤火虫算法; 归一化互信息
中图法分类号: TV542+.4
文献标志码: A
DOI:10.16232/j.cnki.1001-4179.2023.05.033
0 引 言
爆破是硬岩隧道掘进、水电站建设[1-3]、露天及地下矿山开采[4-5]领域中最常见的破岩方法。炸药在岩体内部爆炸时,仅有20%左右的能量用于岩石破碎,80%的爆炸能量以飞石、振动和空气超压等形式耗散[6]。其中,爆破振动可诱发边坡失稳[7-8]、地下构筑物及管线破坏等一系列次生灾害[9-10]。因此,有必要对爆破振动进行有效预测,以便开展爆破振动控制[11]。
在爆破振动预测领域,长期以来一直使用统计预测方程,日本、美国、瑞典等国学者总结归纳了多种爆破振动经验预测方程,并在各类工程中得到了广泛应用[12-13]。尽管经验方程充分考虑了场地条件,但通常只考虑药量和爆心距这两个基本参数,忽略了装药结构和孔网间距等参数对爆破振动的影响,从而导致爆破峰值质点速度预测值与实测值往往存在一定偏差。
近年来,随着人工智能技术的不断进步,爆破振动预测研究重心正逐渐由经验公式推导向非线性智能预测转变。BP神经网络[14-15]、随机森林方法[16]、支持向量回归[17]、自适应神经模糊推理系统[18]等机器学习方法被引入爆破振动预测领域,并取得了良好的预测效果。其中,BP神经网络因其原理简单、操作方便,在基础设施建设[19]、矿山开采[20]等领域岩体爆破开挖工程振动预测中得到了广泛应用。基于此,一些研究人員还开发了基于BP神经网络的爆破振动预测软件[21-22]。尽管BP神经网络的可用性已得到了证明,但在BP神经网络中,初始权值和阈值的选取会极大地影响爆破振动预测结果[23]。因此,有必要对BP神经网络的初始权值和阈值进行优化,得到最优权值和阈值。
本文以砂岩矿区露天台阶爆破为工程背景,全面选取影响爆破峰值质点速度的8个因素作为输入量,构建了基于萤火虫算法优化的BPNN预测模型,用以预测爆破峰值质点速度,并对比了其他3种方法的预测效果,验证了FA-BPNN模型的优越性。此外,还分析了各输入参数对FA-BPNN预测结果的敏感性。研究成果能为台阶爆破岩体开挖安全控制提供参考。
1 FA-BPNN预测模型
1.1 反向传播神经网络
反向传播神经网络(也称BP神经网络,BPNN)是一种前馈神经网络,一般由输入层、中间层和输出层组成[24-25]。BP神经网络中各层包含多个神经元,输入层和中间层、输出层神经元之间全部互相连接,但各层中的神经元无连接,BP神经网络的拓扑结构如图1所示。BPNN模型可通过学习已有输入数据,基于误差梯度函数建立输入数据和输出数据之间的映射关系,从而实现对特定参数的预测。BPNN模型通常包含正向传播和反向传播。使用BP神经网络进行预测时,通常应先初始化权值和阈值,然后进行训练。当输出值与输出期望结果差距较大时,则进入误差判定,开始反向传播,通过不断修正中间层的权值,使总误差最小,从而达到预测的目的。
2 萤火虫算法优化的BPNN模型构建
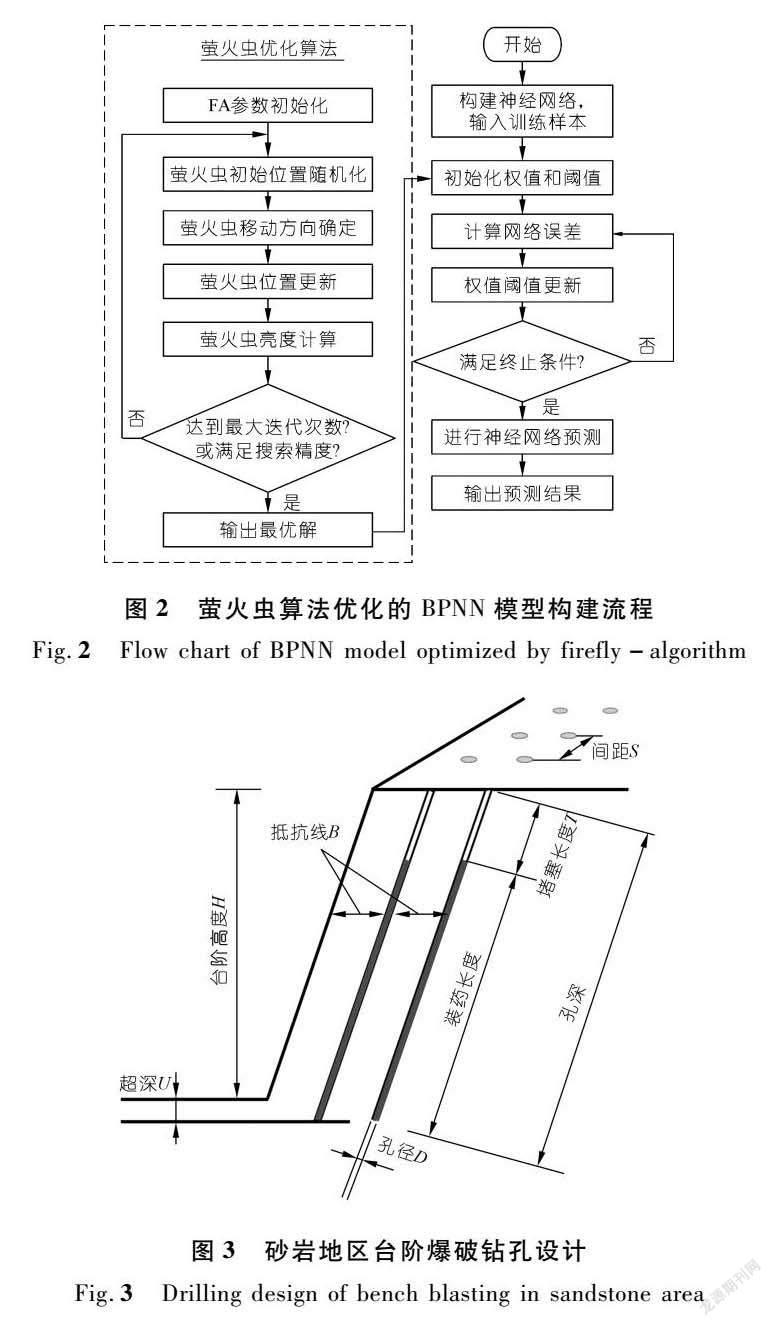
借助萤火虫算法优化BPNN模型时,利用萤火虫算法寻优得到BP神经网络的最优权值和阈值,再通过BP神经网络建立各输入参数与爆破峰值振速的非线性关系,从而实现爆破振动峰值振速预测,对应流程如图2所示。
使用萤火虫优化算法优化BPNN模型的具体步骤如下:确定BP神经网络中间层层数和节点个数,构建BP神经网络;输入训练样本;初始化萤火虫算法参数;开始萤火虫优化,得到最优萤火虫个体对应的最优权值和阈值;输出最优初始化权值和阈值;开展BP神经网络方法预测。
3 爆破峰值振动速度预测
3.1 数据集选取与参数设置
本次爆破振动数据共选取88组露天台阶爆破振动数据[27],试验场地岩体岩石质量指标RQD值约为40~60,爆破对象为砂岩,密度2.7 g/cm3,莫氏硬度约为5~6,孔隙率1.03%,单轴抗压强度81.3 MPa,抗拉强度5.60 MPa,弹性模量16.9 GPa,台阶爆破钻孔示意如图3所示。每组数据集包括9个参数,分别为孔间距与抵抗线长度之比(S/B)、台阶高度与抵抗线长度之比(H/B)、抵抗线长度与炮孔孔径之比(B/D)、堵塞长度与抵抗线长度之比(T/B)、超深与抵抗线长度之比(U/B)、炸药单耗、单段最大装药量、爆心距、质点峰值振速(PPV)。
3.2 FA-BPNN模型预测结果
FA-BPNN模型预测质点峰值振速时,函数适应度值随迭代次数变化情况如图5所示。由图5可知,适应度函数在迭代100次以内就发生收敛,说明使用萤火虫算法优化BP神经网络的权值和阈值时,适应度函数收敛速度快,运算效率高。
由表1可知,FA-BPNN模型预测所得的峰值振动速度与实测爆破峰值振速之间误差较小,平均预测误差仅为12.55%,说明FA-BP神经网络预测模型预测结果能满足实际工程爆破需求。
由图6可知,统计预测方程和随机森林方法对应的爆破振动预测值和实测值误差较大,BP神经网络预测效果较统计预测方程和随机森林更好,但在部分数据点处较FA-BP神经网络预测结果差。整体而言,4种预测方法中FA-BP神经网络预测模型预测效果最好,统计预测方程和随机森林预测效果较差。
为定量评价上述各方法对爆破峰值振速的预测效果,引入均方根误差(RMSE)、平均绝对误差(MAE)和决定系数(R2)作为PPV预测效果评价指标。3种评价指标均可以描述PPV预测值与实测值之间的偏差,当RMSE和MAE越小,R2越大时,说明预测结果较好。
4种爆破峰值质点速度预测方法的各评价指标如表2所列。
5 结 论
本文采用萤火虫算法优化BPNN模型的初始权值和阈值,开发了FA-BPNN爆破峰值质点速度预测模型,并对砂岩区域爆破振动进行预测;比较分析了FA-BPNN模型、统计方程、BPNN模型、随机森林方法的预测结果,并对各输入参数进行敏感性分析,得出以下结论:
(1) FA-BPNN模型能有效预测多因素影响下的爆破峰值质点速度,平均预测误差仅为12.55%,预测效果能满足实际工程爆破需求。
(2) 经萤火虫算法优化的BPNN模型预测结果对应的RMSE和MAE分别为1.445和1.182,R2为0.973,预测准确度优于统计方程、BPNN模型和随机森林等方法。
(3) 单段最大装药量、爆心距、炸药单耗、台阶高度与抵抗线长度之比对爆破峰值质点速度预测效果影响较大,开展爆破振动预测时,除应重点考虑单段最大装药量和爆心距外,还应充分考虑炸药单耗和台阶高度与抵抗线长度之比对爆破振速的影响。
参考文献:
[1] 刘琪,闫俊峰,郭伟,等.泄洪洞顶拱毁损混凝土的爆破拆除技术[J].水利水电快报,2018,39(6):70-73.
[2] 吴新霞,胡英国,刘美山,等.水利水电工程爆破技术研究进展[J].长江科学院院报,2021,38(10):112-120,147.
[3] LI P,LU W B,WU X X,et al.Spectral prediction and control of blast vibrations during the excavation of high dam abutment slopes with millisecond-delay blasting[J].Soil Dynamics and Earthquake Engineering,2017,94:116-124.
[4] 严林,林艺,马洪高.乌东德水电站左岸地下电站机窝开挖技术[J].人民长江,2019,50(增1):242-248.
[5] 钟权,彭峥,刘放.玉瓦水电站引水隧洞爆破开挖损伤特性研究[J].人民长江,2016,47(23):102-106,125.
[6] PARIDA A,MISHRA M K.Blast vibration analysis by different predictor approaches-A comparison[J].Procedia Earth and Planetary Science,2015,11:337-345.
[7] KAHRIMAN A,OZER U,AKSOY M,et al.Environmental impacts of bench blasting at Hisarcik Boron open pit mine in Turkey[J].Environmental Geology,2006,50(7):1015-1023.
[8] 李巖松,罗利,杨根明,等.隧道开挖爆破对临近既有建筑安全影响分析[J].工程爆破,2022,28(1):123-129.
[9] 何理,张微,钟冬望,等.隧道爆破荷载作用下埋地管道动力响应试验[J].工程爆破,2019,25(6):7-13.
[10] 任福国.地铁隧道爆破施工对黄鹤楼振动的影响分析[J].人民长江,2021,52(增2):149-152.
[11] 岳中文,吴羽霄,魏正,等.基于PCA-GA-SVM的露天矿爆破振动速度预测模型研究[J].工程爆破,2021,27(4):22-28,39.
[12] 吴立,陈建平,舒家华.爆破地震效应的实质及其安全距离和破坏标准[J].地质勘探安全,1999(2):21-23.
[13] 胡国忠.城市地下工程爆破的地面爆破震动效应及其震动强度预测[D].重庆:重庆大学,2005.
[14] KHANDELWAL M,SINGH T N.Prediction of blast induced ground vibrations and frequency in opencast mine:a neural network approach[J].Journal of Sound and Vibration,2006,289(4-5):711-725.
[15] MONJEZI M,GHAFURIKALAJAHI M,BAHRAMI A.Prediction of blast-induced ground vibration using artificial neural networks[J].Tunnelling and Underground Space Technology,2011,26(1):46-50.
[16] ZHANG H,ZHOU J,JAHED A D,et al.A combination of feature selection and random forest techniques to solve a problem related to blast-induced ground vibration[J].Applied Sciences,2020,10(3):869.
[17] KOMADJA G C,RANA A,GLODJI L A,et al.Assessing ground vibration caused by rock blasting in surface mines using machine-learning approaches:a comparison of CART,SVR and MARS[J].Sustainability,2022,14(17):11060.
[18] ARMAGHANI D J,MOMENI E,ABAD S V A N K,et al.Feasibility of ANFIS model for prediction of ground vibrations resulting from quarry blasting[J].Environmental Earth Sciences,2015,74(4):2845-2860.
[19] 蒲傳金,郭王林,秦晓星,等.基于BP神经网络的桩基爆破振动速度预测[J].爆破,2018,35(2):177-181.
[20] 王建国,黄永辉,周建明.露天煤矿爆破振动的BP神经网络预测[J].河南理工大学学报(自然科学版),2016,35(3):322-328.
[21] 施建俊,李庆亚,张琪,等.基于Matlab和BP神经网络的爆破振动预测系统[J].爆炸与冲击,2017,37(6):1087-1092.
[22] 胡晓冰,陈志远,魏格平,等.基于BP神经网络的爆破振动预测系统[J].矿业研究与开发,2020,40(9):154-158.
[23] 郭钦鹏,杨仕教,朱忠华,等.运用GA-BP神经网络对爆破振动速度预测[J].爆破,2020,37(3):148-152.
[24] HECHT-NIELSEN R.Theory of the backpropagation neural network[M].Pittsburgh:Academic Press,1992:65-93.
[25] GOH A T C.Back-propagation neural networks for modeling complex systems[J].Artificial Intelligence in Engineering,1995,9(3):143-151.
[26] YANG X S,SLOWIK A.Firefly algorithm[M].Florida:CRC Press,2020:163-174.
[27] HUDAVERDI T.Application of multivariate analysis for prediction of blast-induced ground vibrations[J].Soil Dynamics and Earthquake Engineering,2012,43:300-308.
(编辑:胡旭东)
Abstract:
Blast vibration is a typical harmful effect in rock blast excavation projects.Accurate prediction of blast vibration is of great significance for risk control during blasting.To achieve this goal,the weights and thresholds of the back propagation neural network(BPNN)were optimized with the firefly algorithm(FA),and an FA-BPNN prediction model was established.Taking multiple design parameters and blast center distance of bench blasting in an open-pit mine as the model input parameters,the peak particle velocity(PPV)of blast vibration was predicted,and the prediction results of FA-BP neural network model,statistical prediction equation,BPNN model and random forest method were compared.The sensitivity of each parameter to the prediction results of the FA-BPNN model was analyzed by normalized mutual information.The results indicated that the FA-BPNN model was effective in predicting the PPV,the corresponding root mean square error(RMSE),mean absolute error(MAE),and coefficient of determination were 1445,1182,and 0973 respectively,the FA-BPNN model was more effective than the other three methods.The maximum charge of a single section,the distance between the blasting center,the unit consumption of explosives,and the ratio of step height to the length of resistance line have great influences on the prediction results of the PPV.
Key words:
blast engineering;blast vibration;peak particle velocity;BP neural network;firefly algorithm;normalized mutual information
