基于涌水影响半径的隧道涌水量预测方法研究
2023-05-26张修杰周学民韦未张伟锋
张修杰 周学民 韦未 张伟锋


摘要:
受断裂构造和降水等因素的共同影响,火成岩地区形成了一定规模的富水断层破碎段。当隧道穿越这类岩层时,极易发生涌水灾害而造成人员伤亡和设备损失。针对上述涌水问题,根据火成岩区富水断层破碎段的特点,将隧道涌水量分为基岩裂隙水释放量和降水入渗量两个主要组成部分,通过地下水疏干法预测基岩裂隙水释放量,同时利用降水入渗法预测降水入渗量。在此基础上,为提高涌水预测精度,引入了实测涌水量数据拟合的动态涌水影响半径参与计算,并推导出基于涌水影响半径的涌水量预测方法,最后以鸿图隧道后续开挖段为例对该方法进行验证。研究结果表明:① 在一个降雨周期内,含水层平均厚度Hn越大,对应的影响半径Rn具有更高的增长速率;② 随着涌水时间T增加,影响半径Rn的增长率逐渐降低;③ 所提方法的隧道涌水量计算结果与实际监测数据的误差在10%以内,可靠性较高。研究成果可为类似地质条件下的地下工程建设提供理论指导。
关 键 词:
深埋特长隧道; 涌水量预测; 涌水动态影响半径; 断裂构造
中图法分类号: U452.1+1
文献标志码: A
DOI:10.16232/j.cnki.1001-4179.2023.05.023
0 引 言
隧道在施工过程中会出现一些复杂的施工条件,特别是深埋越岭隧道的穿越建设,破坏了原有围岩的结构,因而施工期常遇见涌水、突水(突泥)等灾害,易造成一系列的恶劣后果[1-2],对人员财产安全构成重大威胁[3-4]。
国内外许多学者都对隧道的涌水进行分析预测:El Tani[5]修正了亥姆霍兹方程,用于研究半无限含水层下圆形隧道的涌水;Joo 等[6]采用层流和紊流的理論方法,研究了孔隙水压力与涌水量的关系;Moon等[7]考虑了地下水位下降与涌水量的关系,提出了新的估算分析方法;胡力绳等[8]探究了地下水、围岩、注浆圈和衬砌共同形成的水压平衡体系中4个因素之间的共同作用;朱成伟等[9]利用保角变换推导了双线平行隧道和上下分布的双洞隧道的地下渗流场;Zhao等[10]通过模型试验和数值模拟分析了地表水存在对隧道衬砌注浆厚度和涌水量的影响;Tan等[11]研究了衬砌的不均匀性与其他水力因素之间的相互作用,用于预测衬砌外水压状况,进而分析出衬砌后隧道涌水量。
对比于其他岩体,拥有较高饱和抗压强度和饱和抗剪断强度的安山玢岩、凝灰岩等火成岩因其坚硬、稳定,通常被认为是理想的地下工程修建区域。修建在火成岩区的隧道、隧洞等地下工程设施一般情况下只在通过构造带、断层富水破碎带、软弱岩层段的时候出现冒顶坍塌、特大突水等安全风险[12-13]。但由于地质勘察和施工设备的局限性、岩体裂隙普遍存在和随机生成的特性,使得难以在施工现场准确识别和确定地下水流入隧道的所有有效因素,部分涌水预测方法存在较大的误差[4,14],给隧道开挖阶段涌水预测带来一定的挑战[15]。
本文以鸿图深埋隧道为研究对象,依据施工前期水文地质勘察对富水断裂带的勘测成果以及开挖期的涌水监测数据,分析一个降雨周期内的涌水特征,探究隧道开挖涌水引起隧址区域地下水位剧烈下降后的地下水降落漏斗影响半径变化规律,并基于曲线拟合手段构建适用于隧道工程穿越断裂带的涌水量计算模型。
1 隧道涌水的传统经验预测
1.1 工程概况
鸿图特长隧道设计全长约6 300 m,最大埋深约为751 m,隧址区地层主要为侏罗系高基坪组火山岩,出露岩石主要为燕山期岩浆岩,形成多期侵入接触带。隧道修建过程中跨越了断层构造发育带,其中东西走向和近南北走向次级断裂和节理发育,岩体破碎。
隧址区水资源丰沛,区内水系分属韩江水系和榕江水系,多年平均降雨量1 865.6 mm,蒸发少,因此岩层富水性较好。水文地质勘察结果显示:隧址区地下水主要为降水补充,地下水类型分为松散岩类孔隙水和基岩裂隙水,地下水补给途径通畅,补给来源充沛。隧道施工过程中也产生了大量的高压涌水,威胁施工安全。
1.2 传统经验预测方法
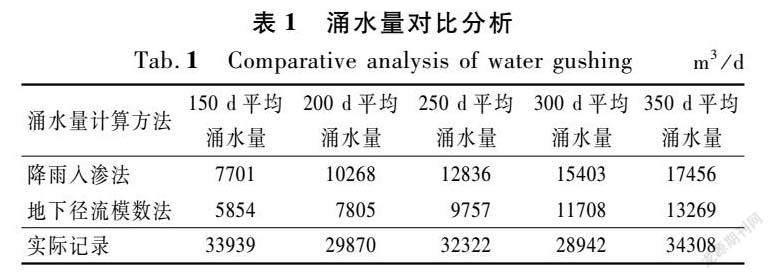
针对隧址区的工程地质和水文地质条件,在施工前期尝试使用传统的降雨入渗法和地下径流模数法来计算不同时间段的单日平均涌水量,为应对隧道施工中涌水量提供参考性意见。但施工现场情况表明,这两种方法与实际涌水量存在较大误差(详见表1)。传统的降雨入渗法和地下径流模数法的计算原理与简易水均衡法一致,本质上属于水均衡法的另一种形式。涌入隧道内的地下水,除来源于大气降水和地表水系之外,还来自于山体的基岩裂隙水。虽然山体的基岩裂隙水同样来源于大气降水和地表水系,但山体的基岩裂隙水是在漫长的地质构造运动中,由大量降水和地表水沿断层破碎带深入岩体内部形成的稳定的地下水体。山体的基岩裂隙水与涌入隧道内的、来源于大气降水和地表水系的地下水存在时空积蓄的差异。传统的降雨入渗法和地下径流模数法在涌水预测过程中没有将这种时空积蓄的差异纳入考虑范畴,也就忽略了基岩裂隙水对隧道涌水量的影响。
当隧道埋深较浅(<50 m)时,基岩裂隙水受限于山体内含水层的规模而储量较小,可忽略不计,传统方法预测隧道涌水量将较为准确;但当隧道埋深较大(>100 m)时,庞大的山体在地质构造运动中足以形成一定规模储量的基岩裂隙水,此时传统方法预测隧道涌水量的准确性将受限于基岩裂隙水的储量。
此外,传统方法在预测隧道涌水量时,均采用固定的汇水面积。汇水面积的估算受水文地质勘察工作的精度影响,而且长期施工过程中,在隧道的涌水影响半径下,地下流场产生复杂的变化,进而使汇水面积也相继发生不同程度的变化,大大影响涌水预测的准确度。
另一方面,在对埋深大(特)长隧道进行涌水预测的过程中,对全隧道段同时进行单日涌水量预测,作为全隧道段单日涌水量的传统方法已不可行。在对埋深大(特)长隧道进行单日涌水量预测时,应该考虑富水断层破碎带区域的分布和施工进度的共同影响,将已开挖段和岩层受扰动隧道段进行分段涌水量预测。隧道分段时,应根据隧道内不同围岩的含水介质特征、围岩性质与级别、推测通过断裂破碎带情况和断裂破碎带宽度及其趋势特征、施工进度等因素划分。为了提高隧道涌水量预测的准确性,针对研究区域特征,引入涌水影响半径概念,结合水文地质勘察结果,以现场实测涌水记录为依据,进行涌水量预测研究。
2 涌水影响半径规律
2.1 基本设定
隧址区含水层规模大,含水层中裂隙网络发育,渗透性良好,基岩裂隙水储量巨大。在隧道开挖涌水后,将引起隧址区域地下水位的剧烈下降,涌水影响半径随之增大,地下水的汇水面积也不断扩大,庞大的山脉以及发育的断层构造保证了岩体深部地下水补给的稳定。当获得新的补给量与隧道涌水量之间已经达到新的动态平衡时,就会形成新的动态稳定流场,隧道涌水量将维持一个相对动态稳定的状态。
隧址区储存的大量基岩裂隙水具有丰富的降雨补充、低蒸发与地下水多级分水岭的特点,遵循水均衡法的基本原理,对研究区域作如下假定。
(1) 隧道上方岩体的给水度一定时间内不发生变化,地下水持续、及时地沿断层构造补充到隧道上方岩体中。
(2) 隧址区岩体含水层之间的水力联系一定时间内不发生变化,只与固有的地质构造有关,但在地下水长时间流动情况下,构造裂隙仍会发生变化。
(3) 隧址区地下水水头在一定时间内不发生骤变,处于基本稳定状态。
(4) 拟建隧道高程以下水系、基岩裂隙水不直接对隧道涌水造成影响。
(5) 构造裂隙使邻近岩体之间保持稳定的水力联系同时也产生相互的影响,涌水影响半径在邻近岩体之间呈有梯度的缓慢变化。
2.2 涌水量与影响半径基本关系
隧道的涌水量计算过程中,需要将目标隧道段分段开展研究。假定隧道研究区段涌水总量Q等于隧道各段涌水量Qn的总和。Qn由基岩裂隙水释放量Wn(1)和降雨入渗的补给量Wn(2)两大部分组成。基岩裂隙水释放量Wn(1)采用地下水疏干法计算,降雨入渗补给量Wn(2)采用动态影响半径的降雨入渗法计算,预测带中的含水层厚度为平均含水层厚度,其计算公式如下:
2.3 计算参数选取
在2.2节中已经明确了隧道涌水量与影响半径等参数的关系式,本节将说明计算过程所需参数的选定情况。
(1) 计算分段划分。根据隧道内不同围岩的含水介质特征、围岩性质与级别、推测通过断裂破碎带情况和断裂破碎带宽度及其趋势特征、施工进度等因素划分计算段。把入口至K91+285段已开挖隧道段和岩层受扰动隧道段沿线分为N个预测计算段,各段长度Ln为10~110 m。随着隧道的不断掘进,N会不断增大,最终N个分段的总长度将等同于隧道实际开挖长度。研究时间从隧道内的第1次涌水开始,设置5个研究节点,研究节点分布如下:① T=150 d,N=23;② T=200 d,N=24;③ T=250 d,N=25;④ T=300 d,N=26;⑤ T=350 d,N=27。
(2) 计算参数确定。根据工程地质和水文地质勘察资料,各区段具体选取参数如图1所示。各分段参数选取说明如下:① 各火山岩富水裂隙段和富水断层破碎段含水层平均厚度为11~587 m;② 研究段岩体给水度为0.001~0.025;③ 表层风化岩层降水入渗系数为0.2~0.3;④ 隧址区多年平均降雨量为1 865.6 mm。
3 现场涌水验证
为验证式(13)涌水影响半径的拟合精确度,选择该隧道后续施工段K91+700~K91+950进行验证,通过对比涌水量计算值与实际监测值进行评估。该安山岩段总长250 m,共施工掘进42 d;受张性断层F2-5的影响,该段岩体破碎,在地下水持续补充作用下,形成了富水断层破碎带。根据岩体给水度差异,以0.000 5 的差异梯度为划分标准,将250 m长的富水断层破碎带划分为接续的6段,记录施工过程中各段揭露富水裂隙区域和富水断层破碎区域产生涌水的时间,忽略邻近隧道段渗水量影响,具体参数详见表3。
将表3的参数代入式(10)中,得到该施工段影响半径随涌水时间的变化值,截至42 d时计算得涌水影响半径最大为808 m。
将各时间点下涌水影响半径的计算结果代入式(13)中得出K91+700~K91+950段涌水量计算值。为验证计算结果的正确性,将涌水的实际监测值与涌水计算值进行对比,如图4所示。
由图4可以看出:在42 d内涌水计算值曲线的变化趋势与实际监测值曲线的变化趋势基本一致,两者均随涌水时间增加而不断减少;在涌水的1~6 d内涌水计算值略大于实际监测值,平均误差为7%;7~42 d涌水实测结果存在一定的波动情况,但整体上与计算值结果较为接近,整体最大误差不超过5%。
两曲线存在误差的原因如下:① 当岩体裂隙网络发达、围岩给水度较大时,分段围岩之间存在一定的连通性,开挖扰动区域裂隙后,使得周边富水断裂带中的基岩裂隙水沿岩体裂隙网络涌入到隧道内,导致实测结果存在一定的波动情况。② 实测值是点监测,而数学模型属数理统计,本身存在系统误差,但总体上模型计算与实际监测值相近。
4 结 论
(1) 在涌水量预测计算中,汇水面积应采用动态面积,动态变化因素为涌水影响半径。在一个降雨周期内,含水层平均厚度Hn对影响半径Rn的影响逐渐显著,Hn越大,对应的Rn将具有更高的增长速率;随着涌水时间T增加,影响半径Rn的增长率逐渐降低,涌水影响半径总体呈非线性增加。
(2) 定义的6 d处拐点和170 d处拐点,把隧道涌水时间段较为准确地分为3段,分別为特大涌水量时间段、较大涌水量时间段及缓增涌水量时间段。
(3) 在埋深大且受富水断层裂隙联动影响下,为提高一个降雨周期内的涌水影响半径计算精度,施工中应及时判断富水断裂带规模,以提高涌水预测评估的准确性。
(4) 对存在于火成岩富水断层裂隙区域内的破碎岩体,施工过程中及时加固并进行锚固支护,减少隧道基岩裸露长度,对于减少隧道内涌水量尤为重要。
参考文献:
[1] 刘志春,王梦恕.隧道工程因素对地下水环境影响研究[J].岩土力学,2015,36(增2):281-288.
[2] 张顶立,孙振宇,宋浩然,等.海底隧道突水演化机制与过程控制方法[J].岩石力学与工程学报,2020,39(4):649-667.
[3] NIKVAR H A,KATIBEH H,FARHADIAN H.Numerical analysis of steady-state groundwater inflow into Tabriz line 2 metro tunnel,northwestern Iran,with special consideration of model dimensions[J].Bulletin of Engineering Geology and the Environment,2016,75:1617-1627.
[4] FARHADIAN H,KATIBEH H.New empirical model to evaluate groundwater flow into circular tunnel using multiple regression analysis[J].International Journal of Mining Science and Technology,2017,27(3):415-421.
[5] EL TANI M.Helmholtz evolution of a semi-infinite aquifer drained by a circular tunnel[J].Tunnelling and Underground Space Technology,2010,25:54-62.
[6] JOO E J,SHIN J H.Relationship between water pressure and inflow rate in underwater tunnels and buried pipes[J].Géotechnique,2014,64(3):226.
[7] MOON J,FERNANDEZ G.Effect of excavation-induced groundwater level drawdown on tunnel inflow in a jointed rock mass[J].Engineering Geology,2010,110(3):33-42.
[8] 胡力繩,王建秀,卢耀如.考虑地下水、注浆及衬砌影响的深埋隧洞弹塑性解[J].岩土力学,2012,33(3):757-766.
[9] 朱成伟,应宏伟,龚晓南,等.水下双线平行隧道渗流场解析研究[J].岩土工程学报,2019,41(2):355-360.
[10] ZHAO X,YANG X.Experimental study on water inflow characteristics of tunnel in the fault fracture zone[J].Arabian Journal of Geosciences,2019,12(13):399-411.
[11] TAN Y Q,SMITH J V,LI C Q,et al.Predicting external water pressure and cracking of a tunnel lining by measuring water inflow rate[J].Tunnelling and Underground Space Technology,2018,71:115-125.
[12] 蔡俊华.穿越花岗岩蚀变带的隧道突涌机理及施工许可评价方法研究[D].武汉:中国地质大学(武汉),2018.
[13] 胡义新,陈培帅.小净距隧道富水破碎带突水灾变演化规律与防治技术[J].公路,2016,61(7):325-329.
[14] 谢伟,杨绪波.基于解析法对折多山隧道进行分段涌水量预测计算[J].公路,2019,64(4):318-32.
[15] 程小勇,黄勤健.深埋隧道断裂带涌水量预测分析[J].人民长江,2021,52(8):133-136,150.
(编辑:刘 媛)
Abstract:
Under combined influences of fracture tectonics and precipitation,a certain scale water-rich faults have been formed in the igneous region.When tunnels pass through such regions,it is highly possible to cause water gushing and loss of life and equipment.For the above water gushing problems,according to the analysis of the water-rich fault fracture section characteristics in the igneous area,the tunnel water gushing was considered to be composed of two major components:those released from bedrock fractures and those from precipitation infiltration.The former was predicted by the groundwater desiccation method,while the latter was predicted by the precipitation infiltration method.On this basis,in order to gain a higher accuracy of the prediction results,the influence radius fitted by the measured data was involved in the calculation,and a method for water gushing prediction was deduced based on the influence radius.Finally,an example of Hongtu Tunnel was illustrated for verification.The results showed that:① within a rainfall cycle,the larger average thickness of the aquifer(Hn)there was,the higher growth rate of the corresponding influence radius(Rn)would be.② With the increase of the time T,the growth rate of the radius of influence Rn was gradually reduced.③ The error of the calculation results of the proposed method and the actual monitoring data was within 10%,and the accuracy was high.The research results can provide theoretical guidance for the construction of underground projects under similar geological conditions.
Key words:
deep-buried long tunnel;prediction of water gushing;dynamic influence radius of water gushing;fracture structure
