UHPFRC 圆盘动态劈裂试验及基于μXCT 图像的破坏机理研究*

2023-05-25杨贞军李雅祺喻渴来

爆炸与冲击 2023年5期

姚勇，杨贞军，张昕，庞苗，李雅祺，喻渴来

（1. 浙江大学建筑工程学院，浙江杭州 310058；2. 武汉大学土木建筑工程学院湖北省岩土与结构安全重点实验室，湖北武汉 433000）

超高性能纤维增强混凝土（ultra high performance fibre reinforced concrete, UHPFRC）自20 世纪90 年代年诞生以来，受到了越来越多的关注[1-3]。UHPFRC 通常由水泥、细砂（平均粒径小于0.5 mm）、硅灰、石英粉、高效减水剂、水（一般水胶比不高于0.2，胶凝材料包括水泥和硅灰）和高强钢纤维按一定比例制备而成[4]。与普通混凝土相比，UHPFRC 具有超高的抗拉强度（6～12 MPa）、抗压强度（120～200 MPa）和耐久性（使用寿命200 年以上），其直接拉伸峰值应变可达3%以上，断裂能可达40 kJ/m2，是一种优越的抗冲击和抗爆结构材料[5-9]。

目前，对UHPFRC 材料的静态力学性能研究日趋成熟，而对其动态力学性能的研究有限，且大多采用分离式霍普金森压杆（split Hopkinson pressure bar, SHPB）进行单轴压缩冲击试验[10-14]；而一般冲击和爆炸等动态荷载在结构中产生压缩和拉伸应力波，因此材料的动态拉伸性能对防护结构的安全也至关重要。然而，由于混凝土试件与拉杆之间的有效连接（多采用胶黏[15]）很难保证，采用霍普金森拉杆很难实施动态直接拉伸试验，因此多采用劈裂试验对动态拉伸行为进行研究。如焦楚杰等[16]、巫绪涛等[17]和Khosravani 等[18]采用SHPB 动态劈裂试验，发现UHPFRC 试件的动态劈裂强度是静态强度的1.22～1.51 倍（2～8 m/s 冲击速率），动态抗拉强度增强因子（dynamic increase factor, DIF）较普通强度混凝土低。Park 等[19]发现在高应变率下，基体强度较低的UHPFRC 试件具有更高的DIF。Cadoni 等[20]研究了纤维体积含量的影响，发现劈裂强度和能耗均随纤维含量的提高而增大。黄政宇等[21]和Su 等[22]发现UHPFRC 试件劈裂拉伸强度与破坏面上钢纤维的平均间距有关，间距越小，强度越高。Tran 等[23-24]和Pyo 等[25]比较了螺旋和光滑直纤维对UHPFRC 试件动态拉伸强度的影响，发现螺旋纤维UHPFRC 试件具有更高的动态拉伸强度和耗能能力。以上研究表明，UHPFRC 材料的动态和静态劈裂破坏机理有明显区别，目前对其动态破坏过程和钢纤维阻裂的微观机理还缺乏深入研究。

作为一种无损检测技术，微观X 射线计算断层扫描（micro X-ray computed tomography, μXCT）能够获得试件内部高分辨率的多相材料（包括孔洞和纤维）的三维形状、大小和分布，近年来被广泛用于各种复合材料的表征，以及荷载下混凝土复杂损坏和断裂机理的研究[26-28]。在纤维混凝土方面，μXCT 已被用来统计分析钢纤维的分布[29]和研究纤维分布对薄板试件抗弯强度的影响[30]。最近，Yang 等和Zhang 等结合μXCT 分别进行了UHPFRC 锲体和小梁试件的原位劈裂[31]和非原位弯曲试验[32]，获得了三维裂缝扩展的全过程及纤维走向对裂缝扩展的影响机理，建立了基于μXCT 图像的细观有限元模型，发现孔洞分布对受弯起裂和扩展有较大影响。但将μXCT 技术应用于UHPFRC 材料动态力学性能的研究还未见报道。

本文中，采用SHPB 进行不同纤维含量UHPFRC 圆盘试件的冲击劈裂试验，获得DIF 和钢纤维含量之间的定量关系；同时采用高速摄像机结合数字图像相关（digital image correlation, DIC）技术，获得表面裂缝扩展全过程图像和应变演化过程；对冲击前后试件进行μXCT 扫描，获得试件内部三维高精度图像，并通过对孔洞、钢纤维及裂缝进行统计分析和可视化表征，阐明钢纤维含量对二、三维劈裂拉伸破坏模式和纤维阻裂机理；以期研究的结果可为UHPFRC 材料在防护工程领域的应用和动态设计规范的完善提供参考。

1 试验

1.1 试件

材料主要包括：P. O 52.5 普通硅酸盐水泥；硅灰，灰白色，含碳量低于2%；细砂，粒径不超过0.5 mm；石英粉，平均粒径约为26.7 μm；聚羧酸高效减水剂，型号为巴斯夫1641F；高强度钢纤维，长12 mm，直径为0.2 mm，密度为7 800 kg/m3，拉伸强度为2 500 MPa。

4 组材料的配合比如表1 所示，其中基体材料的组分及用量一致，钢纤维体积分数分别为0、1%、2%和3%。静力压缩试验的试件分组编号为C0～C3，准静态劈裂和动态劈裂试验的试件编号分别为ST0～ST3 和DT0～DT3。

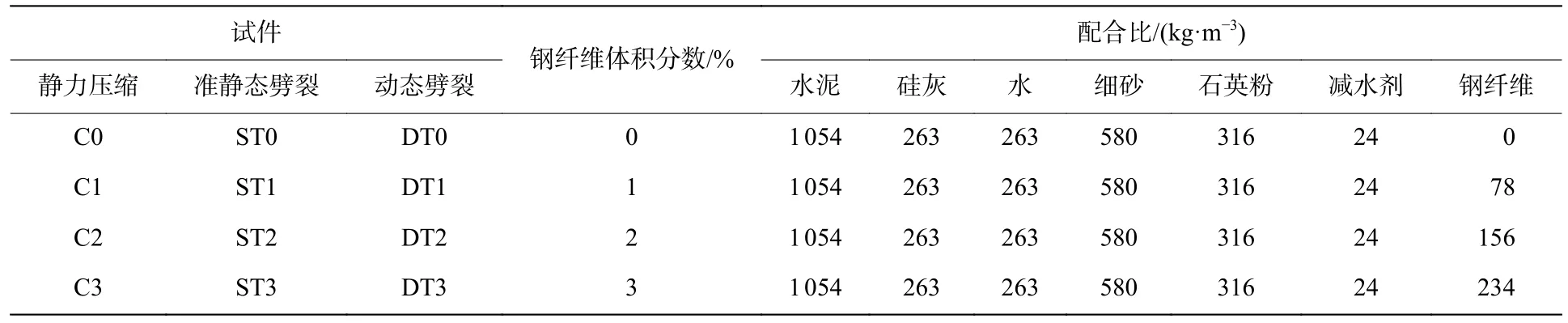
表1 各组UHPFRC 试件的配合比Table 1 Mixing proportions of UHPFRC specimens for each test group

为了保证数据的可重复性，随机选用试件进行编号和试验，不同加载条件下，每组试件进行3 次试验，共制备和加载了36 个试件。

将按表1 配合比准备好的水泥、硅灰、细砂、石英粉倒入搅拌锅内，干拌4 min，再加入固态高效减水剂，干拌2 min。然后倒入一半用水量，搅拌3 min，再加入另一半用水量，搅拌6 min，形成流动性良好的浆体。再分2～3 次加入钢纤维，搅拌6～9 min，确保钢纤维分散均匀，无结团现象。将搅拌好的拌合物倒入尺寸为 ∅ 68 mm×150 mm的圆柱体模具中，在振动频率为50 Hz 的振动台上振捣1 min，使拌合物密实成型。试件在室温中养护24 h 后拆模，移入标准养护环境中（温度为(20±3) ℃，湿度不低于 90%），养护28 d 后取出。将每个圆柱体试样切割成3 个高34 mm、直径68 mm 的圆盘，并对圆盘试样的两侧进行切割，形成环向圆心角为20°的切割面，两侧切割面保持平行，以便进行劈裂加载，见图1。

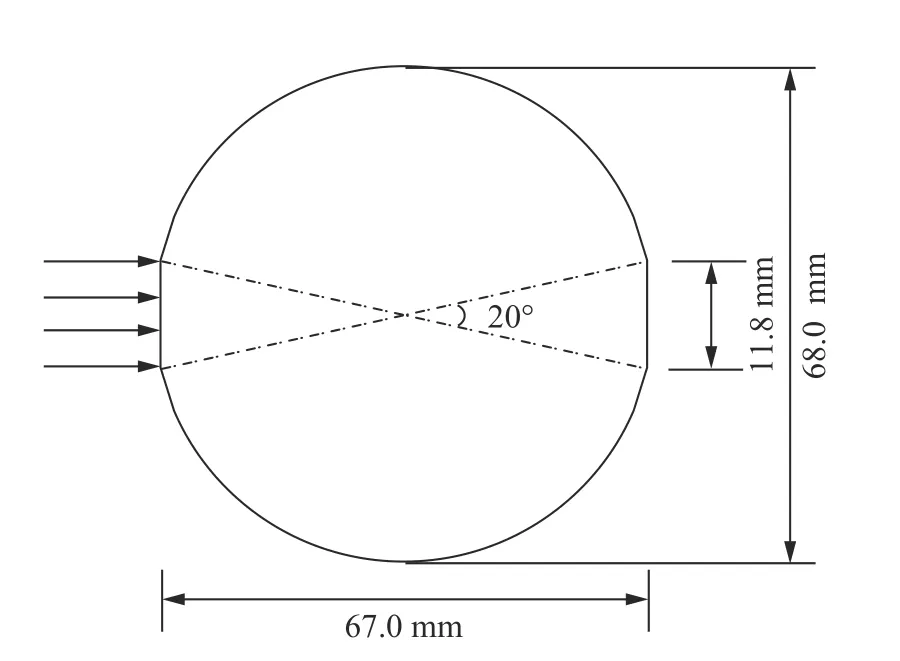
图1 劈裂试件横截面Fig. 1 The cross section of a disc specimen

1.2 静力加载

静力压缩试验在100 t 的Instron 试验机上进行，如图2 所示。圆柱体试件尺寸为 ∅ 68 mm×140 mm，加载速率0.2 mm/min。试件两端面预先采用磨床打磨光滑，并涂抹石膏粉，以减少偏压和端部摩擦带来的影响。在试件表面的中部位置对称粘贴2 片敏感栅长度为5 mm 的竖向应变片测试材料的弹性模量。弹性模量的计算按照标准ASTM C469[33]，以10%和40%峰值应力所对应的2 个数据点的割线模量为试件的弹性模量Es。

图2 静力压缩试验Fig. 2 Quasi-static compression test

静力劈裂试验在24 t 的Instron 试验机上进行，如图3 所示。加载速率0.2 mm/min，预先在加载平台表面涂抹真空脂，以降低端部摩擦的影响。当试件两端切割面所对应圆心角不超过20°时，可忽略其对试件中心点拉伸应力的影响[18,34-35]，根据巴西圆盘劈裂加载的应力解析解，劈裂抗拉强度为：

图3 静力劈裂试验Fig. 3 Quasi-static split test

式中：Fm为劈裂荷载峰值，d为试件直径，h为试件厚度。

1.3 SHPB 冲击劈裂

动态劈裂试验采用直径为50 mm 的SHPB 进行，如图4 所示，试验装置由发射系统、入射杆（长2.0 m）、透射杆（长2.0 m）及吸收装置组成，子弹的冲击气压保持在0.2 MPa。为了提高试样前后端面受力均匀性，并且降低波形弥散对精度的影响，将黄铜片粘贴在入射杆端作为波形整形器，该方法可以有效减缓波形上升坡度[36-37]。

图4 分离式霍普金森杆劈裂试验装置Fig. 4 SHPB splitting test setup

采集入射杆和透射杆上的应变片测得的应变信号，基于弹性压杆的一维应力假定和试件的均匀性假定[38]，试件在加载过程中处于动态平衡状态，则：

式中： εi(t) 、 εr(t) 和 εt(t) 分别为入射波、反射波和透射波的应变信号，t为时间。

采用弹性压杆中的应变信号对式(2) 进行验证，以检查试件的动态平衡状态。采用试件DT1-3 的数据进行验证，如图5 所示， εt(t) 与 εi(t) +εr(t)吻合良好，只在试件因破坏失去承载力后（275～400 μs）出现了一定偏差，这种偏差对动态劈裂强度计算的影响是可接受的。

图5 弹性杆中的应变Fig. 5 Strain in elastic bars

在试件的2 个夹持端面的动态劈裂荷载为：

式中：A为冲击杆的横截面积，E为冲击杆的弹性模量。

将式(3)代入式(1)，得到试件中心点的动态拉伸应力为：

取式(3)中F的峰值Fm代入式(1)，或取式(4)中 σt(t) 的峰值，得到动态劈裂抗拉强度 σT。

借鉴普通混凝土圆盘劈裂试验研究[39-40]，将峰值前的平均拉伸应变率定义为该次试验的应变率：

式中： σ ˙=σT/tm为应力率，tm为劈裂应力达到峰值点的时间。

1.4 高速摄影、DIC 和μXCT 扫描

数字图像相关DIC 通过图像相关匹配的方法来跟踪试件表面标记点的运动，并通过分析材料变形前后的散斑图像得到试件表面的位移和应变分布[41]。在冲击试验前先选择表面缺陷较少的UHPFRC 试件，在表面喷涂一层均匀白色底漆，然后喷洒雾化黑漆作为随机散斑点（见图4(b)）。采用Photron 高速相机（Fastcam Nova S9）拍摄整个冲击过程，采集频率为50 000 s-1，相片分辨率为0.26 mm/像素。对DT0 和DT1 组各1 个试件进行了摄像和DIC 分析。

采用μXCT (Nikon XTH320)扫描仪对冲击试验前后的试件进行扫描，如图6 所示。该扫描仪最高焦点精度为2 μm，每次扫描时电压为180 kV，电流为160 μA，载物台旋转360°，每0.143°扫描一次，共得到2 501 张二维X 射线图，图像分辨率为56.7 μm。采用CT Pro 和VG Studio进行三维重建。对冲击试验前DT0～DT3 组和冲击后DT1～DT3 组各1 个试件进行扫描；DT0 试件不含纤维，冲击后试件碎裂，因而未在试验后进行扫描。

图6 微观X 射线计算断层扫描仪Fig. 6 The micro X-ray computed tomography scanner used in tests

2 结果与分析

2.1 静力试验

如表2 所示，钢纤维掺量的增加可显著提升UHPFRC 材料的静力抗压力学性能。相比无纤维组SC0试件，掺入1%、2%和3%的钢纤维，圆柱体的抗压强度分别提高了11%、30%和45%，弹性模量分别提高了1.6%、11.2%和13.8%，压缩峰值应变分别提高了0.6%、7.9%和10.4%，这与文献[42]的结果基本一致。

表2 静力压缩试验结果Table 2 Results of static compression tests

4 组试件的静力劈裂强度见表3。无纤维组试件ST0 的平均劈裂强度为11.41 MPa，掺入1%、2%和3%的钢纤维使试件的平均劈裂强度分别提高了84%、105%和131%。可见，掺入少量的纤维，即能够大幅度提高UHPFRC 材料的劈裂抗拉强度，钢纤维对UHPC 基体开裂具有强大的约束作用。

表3 静力劈裂试验结果Table 3 Results of static split tests

2.2 劈裂破坏形态

图7 为典型静力劈裂后（ST 组）试件的破坏形态。所有试件出现贯穿主裂缝，其中无纤维试件ST0 沿直径脆断为两部分，裂缝面平直；有纤维试件裂而不散，主裂缝曲折且偏离圆心，显示纤维的桥连作用和随机分布的影响。如图8 所示，动态冲击下（DT 组试件），主裂缝均基本穿过圆心，其中无纤维试件（DT0）中心带状碎裂，而有纤维试件均裂而不散，且随着纤维掺量增加，裂缝宽度减小，表明纤维阻裂效果明显。还发现，冲击下纤维的存在和随机分布对裂缝扩展路径的影响比静态加载下要小，这是因为冲击荷载下中心主裂缝扩展迅速，且横向惯性力效应抑制了部分微裂缝的扩展及主裂缝偏折的趋势，这使得动态劈裂下主裂缝更平直[43]。

图7 静力劈裂后的试件Fig. 7 Specimens after quasi-static splitting

图8 动态劈裂后的试件（冲击应变率为1.72～7.42 s-1）Fig. 8 Specimens after dynamic splitting at the strain rates of 1.72－7.42 s-1

图9～10 分别显示了由高速摄影和DIC 技术结合获得的试件DT0 和DT1 在冲击过程中竖向应变（εy）云图的演变过程和裂缝形成过程，可见裂缝均在圆心产生，然后向两端扩展，最终形成了贯穿主裂缝。不同的是，无纤维DT0 试件在贯穿主裂缝产生之后，其上、下两侧继续产生新的次生裂缝，最终形成较宽的破碎带；而有纤维试件虽然在主裂缝附近一定范围内产生高应变区，但因纤维的约束和桥连作用没有形成次生裂缝，因而基本保持完整。

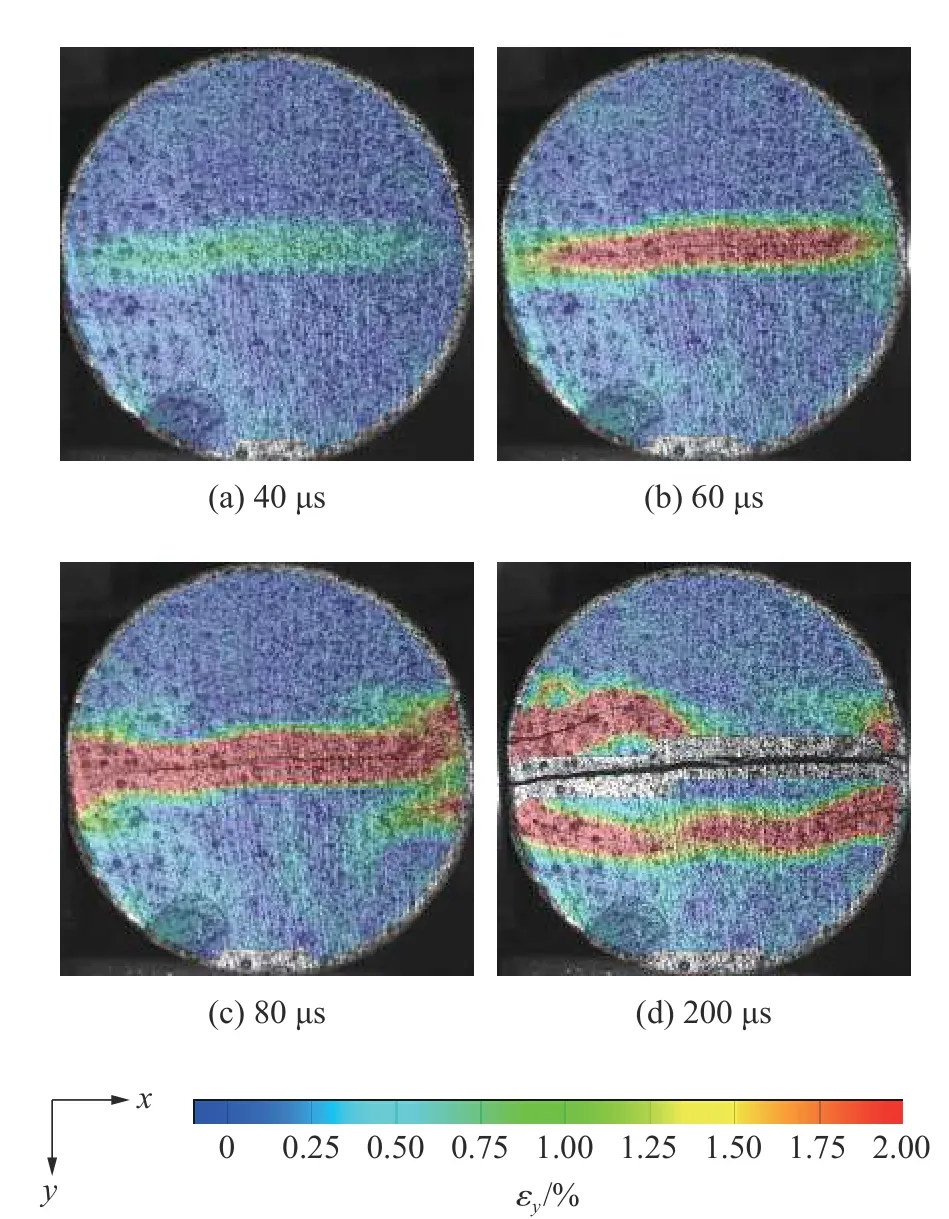
图9 由高速摄影和数字图像相关技术结合获得的试件DT0-3 开裂过程和竖向拉应变场演化Fig. 9 Crack and vertical tensile strain field evolutions in specimen DT0-3 by combining the high-speed video and digital image correlation techniques

以上由高速摄影和DIC 技术应变云图演化显示的表面裂纹产生、快速扩展和贯穿破坏的过程，证明了巴西圆盘冲击劈裂试验中，裂纹由中心点起裂并向两端扩展的特性。这是高速冲击试验中采用肉眼观测所发现不了的。

2.3 动力响应

图11 为各组材料3 个试件中心劈裂应力时程曲线。无纤维DT0 组试件脆性破坏，含纤维DT1～DT2组试件劈裂应力达到第1 个峰值后存在一段多峰波动平台，Tran 等[23]也发现了类似现象。这是因为试件在出现裂缝后，钢纤维的阻裂和桥连效应延缓了裂缝扩展，试件内部应力波震荡导致了多峰出现[38]。此外，DT3 组试件纤维含量较高，表现出较强的应力强化，这在文献[21-23, 25-27]中也有发现。

图11 DT0～DT3 组试件劈裂应力-时间曲线Fig. 11 Splitting stress-time curves of specimen groups DT0－DT3

表4 汇总了各组试件的峰值应力（即动态劈裂抗拉强度 σT以及平均动态劈裂强度 σT,a）、由方程(5)计算的平均应变率（ ε˙ ）和动、静力劈裂强度的比值即动态强度增强因子δt。可见，各组材料的动力劈裂强度均大于其静力强度(δt＞1)，其中有纤维的DT1～DT3 组试件的δt在1.07～1.17，小于无纤维DT0 组试件的1.32～1.72。各组试件的平均应变率 ε˙ 在1.72～7.42 s-1。本文的应变率波动范围小，对同组试件动态劈裂强度的影响可以忽略。因此，可对各物理量取平均值，并计算其标准差。

表4 动态劈裂试验结果Table 4 Results of dynamic split tests

2.4 钢纤维对劈裂强度及能耗的影响

各组试件劈裂强度与钢纤维体积含量的关系如图12 所示。钢纤维体分数分别为1%、2%和3%的试件的静劈裂强度比无纤维试件（ST0）的静劈裂强度分别提高了84%、106%和131%，动劈裂强度则分别较无纤维试件（DT0）的动劈裂强度提高了47%、54%和87%（见表4）。

图12 试件劈裂强度与钢纤维掺量的关系Fig. 12 Splitting strength of specimens varied with steel fibre content

定义钢纤维增强因子为：

式中： σ (φ) 为钢纤维体积分数为 φ 的圆盘试样的劈裂强度， σ0为无纤维UHPC 基体圆盘试样在相同加载条件下的劈裂强度。对数据采用二阶多项式拟合，得到图13 所示钢纤维增强因子δsf和钢纤维体积掺量 φ 之间的抛物线关系式。

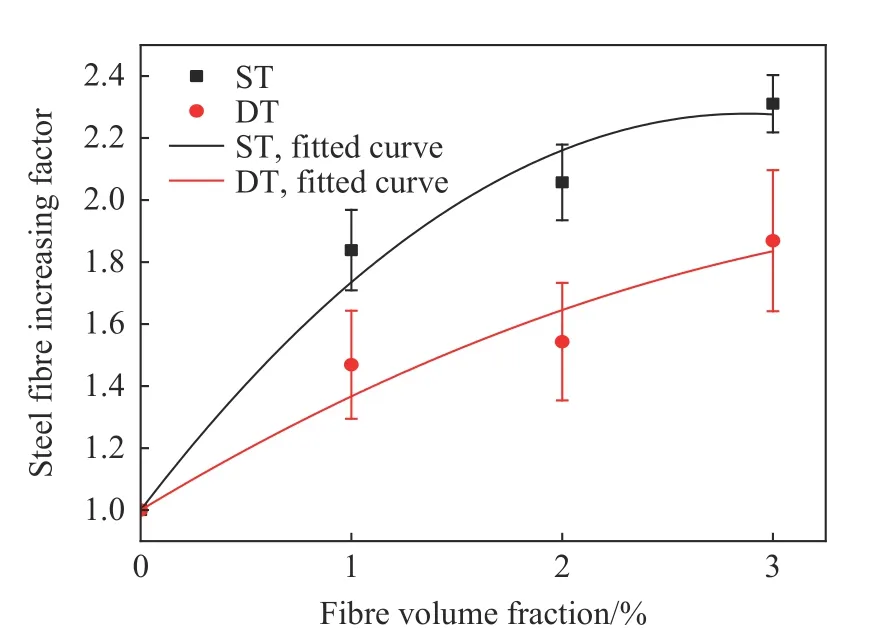
图13 钢纤维对试件劈裂强度的增强效应Fig. 13 Enhancement effect of steel fiber on splitting strength of specimens

静力加载:

动态加载:

从图13 可以看出，钢纤维掺量对对静劈裂强度的增强效应比对动劈裂强度的增强效应明显。静力加载下，跨裂缝的纤维缓慢拔出，其阻裂作用得以充分发挥，导致较好的增强效果；而动态加载下，因应力波的快速传播和惯性效应，初裂缝来不及扩展就产生较多的新裂纹，导致纤维阻裂作用降低，纤维的增强效果因而相对较差，这与文献[37]中的结论一致。

试验冲击气压恒定，子弹的冲击速度波动很小，因此可忽略子弹速度变化对试件动能的影响。动态劈裂试验的能量耗散W(t)计算方式如下[17]：

式中：c0为弹性波在杆件中的传播速度，c0=5 667.2 m/s。

图14 为钢纤维掺量和劈裂能耗的关系，可见劈裂能耗随钢纤维掺量的增大呈单调上升趋势，DT1、DT2 和DT3 组试件的劈裂能耗较DT0 组（11.1 J）分别提高了184%、222%和390%。相比对强度的提高，纤维掺量对劈裂能耗或者试件延性的提高更明显。

图14 UHPFRC 的动态劈裂平均能耗Fig. 14 Average energy consumption of UHPFRC in dynamic splitting

3 基于μXCT 图像的结果分析

3.1 图像处理、分割和统计分析

首先，使用CT Pro 软件将扫描得到的二维投影图重构为3D 图像；然后，使用Avizo 软件对3D 图像进行裁剪、降噪和过滤等处理。作为示例，图15(a)显示了处理后的DT1-3 试件（冲击加载前）外观图像，裁剪后的直径为65.8 mm，厚度为33.6 mm；图15(b)显示了3 个法平面上的典型灰度图，并标注了纤维、孔洞和砂浆。

图15 经裁剪、降噪和过滤处理后的μXCT 图像Fig. 15 The μXCT images after cropping, filtering, and segmentation

根据材料组分的灰度阈值进行μXCT 图像分割，以图16～17 为例说明确定组分材料灰度阈值的方法，图像为8 比特灰度图，灰度值范围为0～255。线段AB穿过钢纤维、砂浆和孔洞，沿线灰度值为40～160。因钢纤维和砂浆基体密度差别较大，钢纤维的灰度阈值较易确定，为115。孔洞的灰度阈值范围约为60～80。为了进一步确定孔洞的灰度阈值，采用灵敏度分析[32]。图17 显示了采用不同阈值所计算的试件DT1-3 孔洞体积分数和灰度阈值的关系曲线，采用四阶多项式进行拟合。在二阶导数为零的点，孔洞体积分数对灰度值阈值的变化最不敏感，因此可将该阈值作为孔洞分割的最佳阈值。如果使用较低的阈值，识别的孔洞将不完整；反之，则更多的砂浆基体将被误识别为孔洞。对于试件DT0-3、DT1-3、DT2-3 和DT3-3 的图像，确定的孔洞最佳灰度阈值分别为68、71、71 和73。

图16 纤维和孔洞灰度阈值的初步确定Fig. 16 Initial determination of grey thresholds for pores and fibres

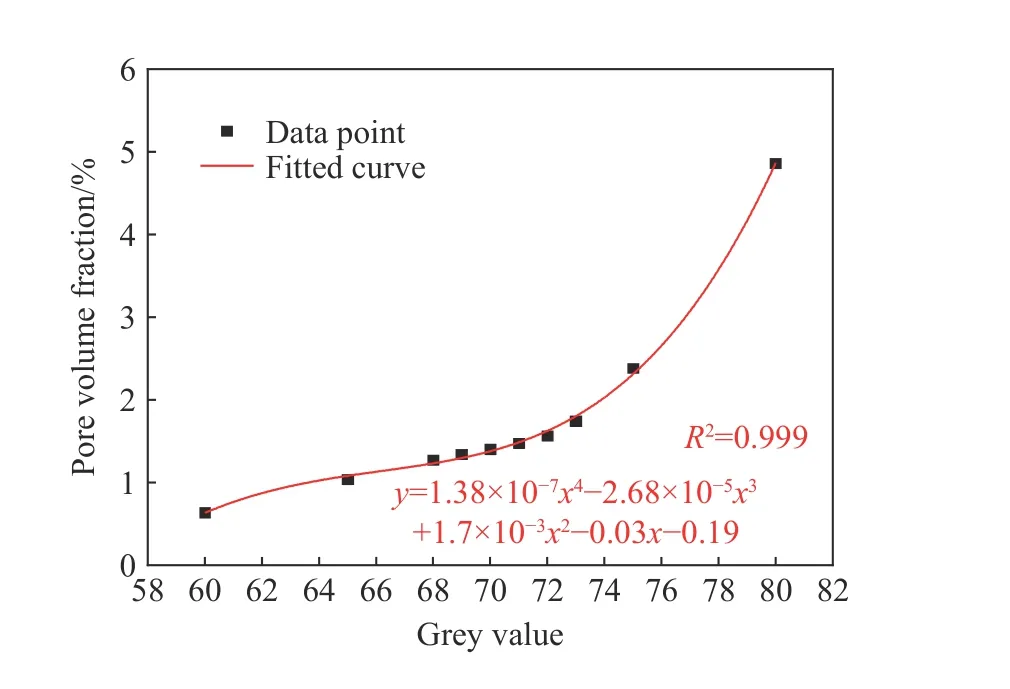
图17 孔洞体积分数对灰度阈值的灵敏度分析Fig. 17 Sensitivity analysis of pore volume fraction to the grey threshold

在孔洞灰度阈值确定后，对内部孔洞进行分割，然后对孔洞信息进行统计和分析，结果如表5 所示。图18 为试件DT0-3～DT3-3 中孔洞等效直径（de）的频数分布。可见，UHPFRC 材料虽然孔洞数目很多，但大孔洞极少，且孔洞之间互不相连，这是该材料致密性、抗渗性和抗侵蚀性强的重要原因[44]。还可以看出，随着纤维掺量的提高，孔洞数量和总体积分数降低，但孔洞的平均体积和平均等效直径增大。这是因为，更多的纤维在基体中分布不均匀，且降低了基体流动性，从而增大了孔洞的平均尺寸和形成大孔洞的概率，这与文献[45-46]一致。图19 为试件DT0-3～DT3-3 孔洞的3D 图像，可见大部分小孔洞接近球形或椭球，不规则大孔洞很少。由于本次试验中μXCT 扫描像素分辨率为56.7 μm，等效直径小于该值的孔洞无法被识别和统计。

图18 孔洞等效直径的频数分布Fig. 18 Frequency distribution of pore equivalent diameters

图19 试件DT0-3～DT3-3 分割后孔洞3D 图像Fig. 19 Segmented 3D images of pores for specimens DT0-3－DT3-3

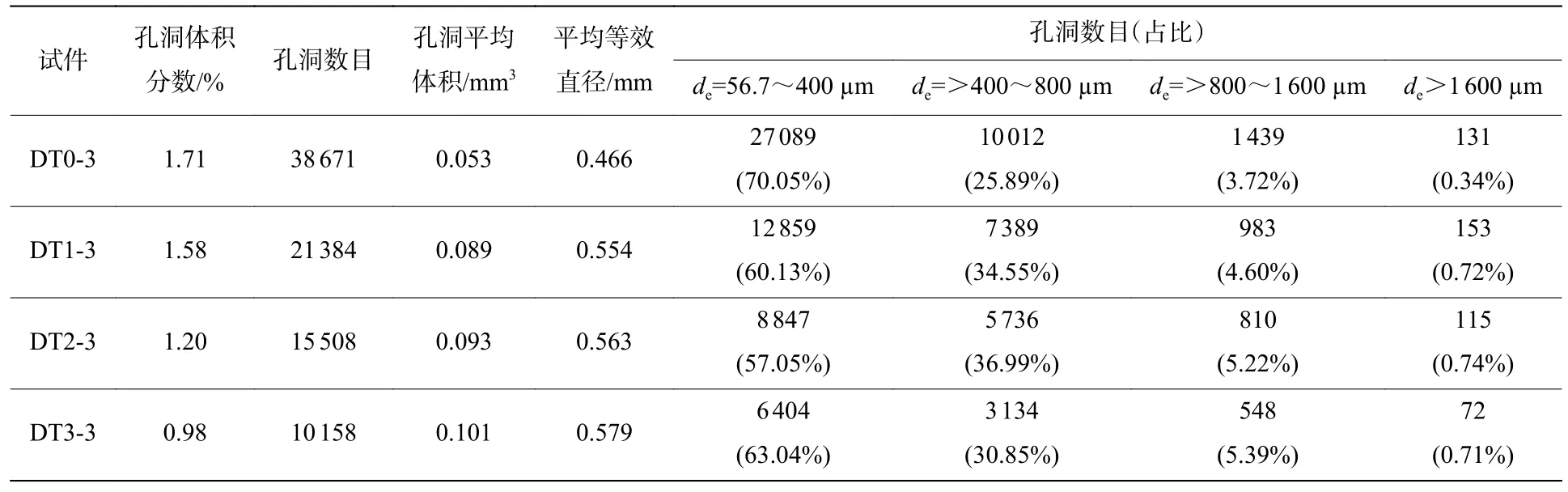
表5 试件DT0-3～DT3-3 孔洞分布统计Table 5 Statistics of pore distribution of specimens DT0-3－DT3-3

采用与孔洞类似的分割方法，对试件DT1-3、DT2-3 和DT3-3 分别采用分割阈值115、116 和121，如图20 所示，所得纤维的数量分别为5 420、12 914 和16 381，体积分数分别为1.04%、1.86%和2.47%，相较于对应的配合比设计值1%、2%和3%，略有差别。这可能有2 个原因：一是浇筑过程中纤维分布不均匀，二是圆盘试件经圆柱试件切割而来，而浇筑过程中对圆柱试件的振捣可能导致纤维在高度方向分布不均。本文中同组试件力学试验数据的离散性不大，在可接受范围内(见表3～4)，可见这些因素没有对试验结果造成明显影响。

图20 试件DT1-3～DT3-3 分割后的纤维Fig. 20 Segmented 3D images and skeleton of fibres for specimens DT1-3－DT3-3

3.2 二维破坏机理

以冲击后的试件DT1-3 为例，选取在xy平面上的二维μXCT 图像切片，来研究试件的动态破坏形态和纤维的阻裂机理。图21 显示沿试件高度(z轴)方向从下至上第400 张切片的二维图像。可以看出，动态劈裂形成一条贯穿的主裂缝及其附近少量的次裂缝，在与入射杆和透射杆接触的端部少量基体剥离。从图像测得3 张切片（切片200、400 和600）中心点处主裂缝宽度分别为2.74、3.09 和3.35 mm，平均值为3.06 mm。采用同样的图像分析方法，测得试件DT2-3 和DT3-3 试件中心点平均主裂缝宽度分别为1.86 和1.38 mm。这表明增加纤维含量能显著降低试件动态劈裂后的主裂缝宽度。

图21 试件DT1-3 在xy 平面裂缝宽度（切片 400）Fig. 21 Crack width on the xy plane of the specimen DT1-3 (slice 400)

图22～24 展示了切片上加载前、后的钢纤维变化，包括拔出、弯曲和断裂。图22(b)中的纤维因试件开裂而从上半侧基体中被拔出，通过测量纤维拔出后留下的孔道得到纤维与基体的相对滑移为1.91 mm。从图23(a)中测得加载前纤维与水平方向夹角为46.4°，冲击后（图23(b)）下半段纤维被拔出，与水平向夹角增大了17.5°，显示该纤维在裂缝处弯曲。从图24(a)中测得纤维原始长度为11.72 mm，从图24(b)可以看到纤维断裂成2 段，上半段长6.70 mm，下半段长5.52 mm，轴向残余塑性变形为：

图22 纤维从基体中拔出Fig. 22 Fibre pullout from matrix

图23 纤维拔出后弯曲变形Fig. 23 Fibre bending after pullout

图24 纤维断裂Fig. 24 Fibre breakage

3.3 三维破坏机理

对试件DT1-3～DT3-3 主裂缝及跨过裂缝的桥连纤维进行三维可视化和统计分析，进一步探讨破坏机理。表6 统计了这3 个试件中的桥连纤维数量、裂缝体积、裂缝表面积和相对表面积。可见，钢纤维掺量越高，桥连纤维数目越多，破坏后主裂缝体积越小，裂缝相对表面积越大。

表6 裂缝及桥连纤维的统计分析Table 6 Statistical analysis of cracks and bridged fibers

图25～27 显示了3 个试件中的三维裂缝及跨过裂缝的纤维三维形态，其中红色为裂缝，黄色为纤维，蓝色边框为试件的几何中心面（xz平面）。根据裂缝的弯曲程度和完整度，将裂缝沿x方向大致分为A、B和C等3 个区域。从图25 可以看出，裂缝完全贯穿了DT1-3 试件，在桥连纤维较少的区域A和C 基本沿试件中心面扩展，裂缝表面光滑；而在纤维分布相对密集的区域B，裂缝稍微偏离试件中心面，底部最大偏移量（裂缝中心面与试件中心面的最大距离）为3.03 mm。从图26 可以看出，在试件DT2-3中，纤维在区域A分布密集，桥连作用强，裂缝未贯穿试件；在纤维较少的区域B，裂缝偏离中心面，上部最大偏移量为4.06 mm。从图27 可以看到，试件DT3-3 中的裂缝面变得更粗糙，在纤维密集的区域A和B，裂缝明显偏离中心面，最大偏移量为9.87 mm；裂缝在纤维较少的区域C基本沿试件中心面扩展。

图25 试件DT1-3 主裂缝及跨过裂缝的纤维Fig. 25 The main crack and crack-crossing fibres of specimen DT1-3

图26 试件DT2-3 主裂缝及跨过裂缝的纤维Fig. 26 The main crack and crack-crossing fibres of specimen DT2-3

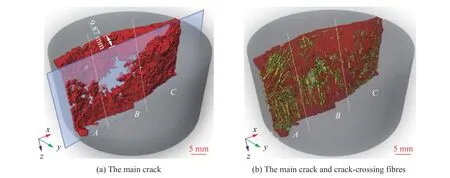
图27 试件DT3-3 主裂缝及跨过裂缝的纤维Fig. 27 The main crack and crack-crossing fibres of specimen DT3-3

从以上μXCT 图像可以看出，随着桥连纤维数量的增加，3 个试件的裂缝面粗糙程度和裂缝与中心面的偏移量增大。这与表6 中的相对表面积的变化规律一致，表明纤维掺量的增加能够显著提高试件的强度（见表4 和图11）、能耗（见图14）、断裂韧性和延性。此外，裂缝趋向于避开纤维密集的区域而向纤维稀疏的区域扩展。