Banach空间中关于m-增生算子零点的黏性隐式迭代序列的强收敛定理
2023-05-24潘灵荣王元恒
潘灵荣,王元恒
(1.浙江开放大学 温岭学院,浙江 温岭 317500;2.浙江师范大学 数学与计算机科学学院,浙江 金华 321004)
1 引言与预备知识
设E是Banach空间,E*是E的对偶空间,对偶映射J:E→2E*定义为
J(x)={f∈E*:〈x,f〉=‖x‖2=‖f‖2},∀x∈E
其中〈·,·〉表示对偶配对。
令C是E的非空闭凸子集,映射f:C→C称为压缩映射,若存在ρ∈[0,1),使得
‖f(x)-f(y)‖≤ρ‖x-y‖,∀x,y∈C
定义映像A:C→E,如果存在j(x-y)∈J(x-y),满足〈Ax-Ay,j(x-y)〉≥0,∀x,y∈C,那么称A是增生算子。如果R(I+rA)=E,∀r>0,那么称A是m-增生算子。记Jr=(I+rA)-1(r>0)为m-增生算子A的预解式,众所周知,Jr是非扩张映射且有F(Jr)=N(A),这里N(A)={x∈E:0∈Ax},F(Jr)是Jr的不动点集,所以非扩张映射的不动点问题可应用到m-增生算子的零点问题[1-3]。
黏滞迭代方法是研究不动点理论和变分不等式问题的重要工具之一,隐中点规则是求解微分代数方程和普通微分方程的计算方法,许多学者将两者结合构造了黏性隐式迭代方法并进行收敛性分析[4-9]。
2016年,JUNG[10]在一致凸Banach空间中引入关于m-增生算子零点和非扩张映射的迭代序列如下:
xn+1=Jrn(αnf(xn)+(1-αn)Sxn),∀n≥0
xn+1=Jrn(αnf(xn)+(1-αn)Sxn+en),∀n≥0
证明了该序列强收敛到m-增生算子零点和非扩张映射的公共点,也是下列变分不等式问题的解。
〈(I-f)p,j(x-p)〉≥0,∀x∈F(S)∩N(A)
2017年,LI[11]在自反Banach空间中,构造关于m-增生算子零点和非扩张映射新的迭代序列。
同年,LUO[12]在一致光滑Banach空间中研究了关于非扩张映射的黏性隐式中点法则,如下:
2018年,ZHANG[13]在上述研究的基础上,在Banach空间中构造了下列迭代序列

在适当的参数条件下,证明了该生成序列的强收敛定理。
受以上结果的鼓舞和启发,我们在Banach空间中给出关于m-增生算子的广义黏性隐式迭代序列
(1)
当满足一定的条件后,证明了序列的强收敛结果,推广和改进了文献[9—13]的相关结论。
为得到本文结果,还需要以下引理。
引理1[14]若λ,μ>0,x∈E,有
引理2[13]令{an},{bn}和{cn}是三个非负实序列,且满足an+1≤(1-tn)an+bn+cn,∀n≥0。这里{tn}⊂(0,1),如果有
那么limn→∞an=0。
引理3[13]Banach空间E是一致凸的,当且仅当存在一个连续严格递增凸函数g: 「0,+∞)|→「0,+∞),g(0)=0,使得
‖λx+(1-λ)y‖2≤λ‖x‖2+(1-λ)‖y‖2-λ(1-λ)g(‖x-y‖)成立。
引理4[15]在Banach空间E中,以下不等式成立
‖x+y‖2≤‖x‖2+2〈y,j(x+y)〉,∀x,y∈E。
这里j(x+y)∈J(x+y)。
引理5[16]设E是自反的一致凸Banach空间,具有一致G-微分范数,C⊂E是非空闭凸集,具有正规结构。设T:C→C是非扩张映射且F(T)≠∅,f:C→C是压缩映射,定义序列{xv}如下:
xv=vf(xv)+(1-v)Tx,v∈(0,1)
该序列强收敛到F(T)上一点p,且p是如下变分不等式的唯一解。
〈f(p)-p,j(q-p)〉≤0,∀q∈F(T)
2 主要结论
定理1设E是自反的一致凸Banach空间,具有一致G-微分范数。C是E中的非空闭凸子集,且具有正规结构。令f:C→C是压缩映像,压缩系数ρ∈[0,1)。A是E中的m-增生算子且N(A)≠∅。对于任一x0∈C,∀n∈N,序列{xn}由(1)式生成,若{αn},{δn},{μn}和{rn}⊂(0,1),{en}⊂E,满足如下条件:

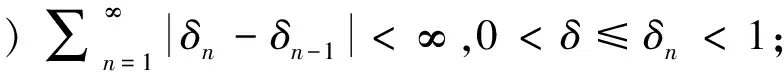

那么序列{xn}强收敛于一点p∈N(A),也是下列变分不等式问题的解。
〈f(p)-p,j(q-p)〉≤0,∀q∈N(A)
(2)
证明证明过程分以下步骤。第一步证明序列{xn},{yn}有界。取p∈N(A),有
‖yn-p‖=‖μnun+(1-μn)Jrn(un+en)-p‖
≤‖un-p‖+(1-μn)‖en‖
≤δn‖xn-p‖+(1-δn)‖xn+1-p‖+‖en‖
由序列{xn}的定义知
‖xn+1-p‖=‖αnf(yn)+(1-αn)Jrnyn-p‖
≤αn‖f(p)-p‖+αnρ‖yn-p‖+
(1-αn)‖yn-p‖
≤δn(1-αn+ραn)‖xn-p‖+αn‖f(p)-p‖+
(1-αn+ραn)(1-δn)‖xn+1-p‖+
(1-αn+ραn)‖en‖
移项整理得
所以{xn}是有界的,从而{f(xn)},{Jrnyn},{Jrnxn},{un},{f(yn)}和{yn}是有界的。
第二步证明limn→∞‖xn+1-xn‖=0。
由式(1)定义可知
‖yn-yn-1‖=‖μnun+(1-μn)Jrn(un+en)-
μn-1un-1-(1-μn-1)Jrn-1(un-1+en-1)‖
≤μn‖un-un-1‖+|μn-μn-1|‖un-1‖+
(1-μn)‖Jrn(un+en)-Jrn-1(un-1+en-1)‖+
|μn-μn-1|‖Jrn-1(un-1+en-1)‖
(3)
和
‖un-un-1‖=‖δnxn+(1-δn)xn+1-
δn-1xn-1-(1-δn-1)xn‖
≤δn‖xn-xn-1‖+|δn-δn-1|‖xn-1‖+
(1-δn)‖xn+1-xn‖+ |δn-δn-1|‖xn‖
=δn‖xn-xn-1‖+ (1-δn)‖xn+1-xn‖+
|δn-δn-1|(‖xn-1‖+‖xn‖)
(4)
根据引理1得
‖Jrn(un+en)-Jrn-1(un-1+en-1)‖
Jrn-1(un-1+en-1)‖
(un-1+en-1)‖
≤‖un-un-1‖+‖en-en-1‖+
≤δn‖xn-xn-1‖+|δn-δn-1|(‖xn-1‖+
‖xn‖)+‖en-en-1‖+ (1-δn)‖xn+1-xn‖+
(5)
结合(3)式,(4)式和(5)式,有
‖xn+1-xn‖=‖αnf(yn)+(1-αn)Jrnyn-
αn-1f(yn-1)-(1-αn-1)Jrn-1yn-1‖
≤αnρ‖yn-yn-1‖+|αn-αn-1|‖f(yn-1)‖+
(1-αn)‖Jrnyn-Jrn-1yn-1‖+
|αn-αn-1|‖Jrn-1yn-1‖
≤|αn-αn-1|(‖f(yn-1)‖+‖Jrn-1yn-1‖)+
Jrn-1yn-1‖+αnρ‖yn-yn-1‖
≤|αn-αn-1|(‖f(yn-1)‖+‖Jrn-1yn-1‖)+
αnρ‖yn-yn-1‖+(1-αn)‖yn-yn-1‖+
≤(1-αn+αnρ) [δn‖xn-xn-1‖+
(1-δn)‖xn+1-xn‖+(1-μn)‖en-en-1‖+
|δn-δn-1|(‖xn‖+‖xn-1‖)+
|μn-μn-1|(‖un-1‖+‖Jrn-1(un-1+en-1)‖)+
|αn-αn-1|(‖f(yn-1)‖+‖Jrn-1yn-1‖)+
从而有
|μn-μn-1|(‖un-1‖+‖Jrn-1(un-1+en-1)‖)+
(1-μn)‖en-en-1‖+
这里
M1=supn∈N{‖f(yn-1)‖+‖Jrn-1yn-1‖}
M2=supn∈N{‖un-1‖+‖Jrn-1(un-1+en-1)‖}
M3=supn∈N{‖Jrn(un+en)-un-en‖}
M4=supn∈N{‖xn‖+‖xn-1‖}
M5=supn∈N{‖Jrnyn-yn‖}
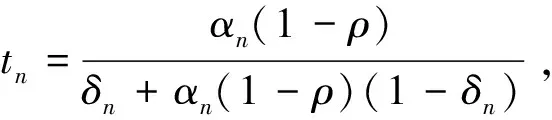
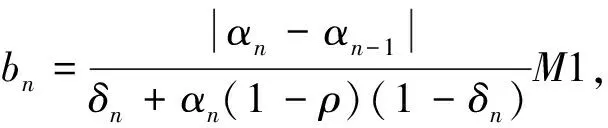
根据条件(i),得到bn=o(tn)。
令
则
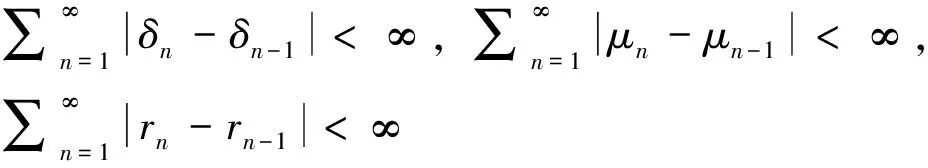
limn→∞‖xn+1-xn‖=0。
(6)
第三步证明limn→∞‖xn-Jrnxn‖=0。
由引理1,引理3,引理4和序列{xn}的定义,
知
‖xn+1-p‖2≤αn‖f(yn)-p‖2+(1-
αn)‖Jrnyn-p‖2
≤αn‖f(yn)-p‖2+(1-αn)‖yn-p‖2
≤αn‖f(yn)-p‖2+μn(1-αn)‖un-p‖2+
(1-αn)(1-μn)‖Jrn(un+en)-p‖2
=αn‖f(yn)-p‖2+μn(1-αn)‖un-p‖2+
(1-αn)(1-μn)·
≤αn‖f(yn)-p‖2+μn(1-αn)‖un-p‖2+
(1-αn)(1-μn)·
≤αn‖f(yn)-p‖2+μn(1-αn)‖un-p‖2+
(1-αn)(1-μn)·
≤αn‖f(yn)-p‖2+μn(1-αn)‖un-p‖2+
(1-αn)(1-μn)‖un+en-p‖2-
≤αn‖f(yn)-p‖2+μn(1-αn)‖un-p‖2+
(1-αn)(1-μn) [‖un-p‖2+
2〈en,j(un+en-p)〉]-
≤αn‖f(yn)-p‖2+(1-αn)‖un-p‖2+
2(1-αn)(1-μn)‖en‖·‖un+en-p‖-
≤αn‖f(yn)-p‖2+δn(1-αn)‖xn-p‖2+
2(1-αn)(1-μn)‖en‖·‖un+en-p‖+
(1-αn)(1-δn)‖xn+1-p‖2-
结合条件(iii),有
2(1-αn)(1-μn)‖en‖‖un+en-p‖-
g(‖Jrn(un+en)-un-en‖)
移项整理得
如果
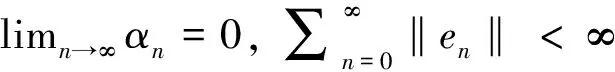
limn→∞g(Jrn(un+en)-un-en‖)=0。
如果
有
‖xN+1-p‖2≤‖x0-p‖2<∞
所以,得
即有
limn→∞g(‖Jrn(un+en)-un-en‖)=0。
根据g的性质,可知
limn→∞‖Jrn(un+en)-un-en‖=0
(7)
观察
‖Jrnxn-xn‖≤‖xn-un-en‖+
‖un+en-Jrn(un+en)‖+‖Jrn(un+en)-Jrnxn‖
≤2(1-δn)‖xn-xn+1‖+2‖en‖+
‖Jrn(un+en)-un-en‖
limn→∞‖xn-Jrnxn‖=0
(8)
第四步证明limn→∞‖yn-Jrnyn‖=0。
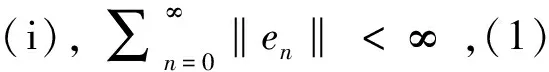
limn→∞‖un-xn‖=limn→∞(1-δn)‖xn+1-
xn‖=0;
limn→∞‖xn+1-Jrnyn‖=limn→∞αn‖f(yn)-
Jrnyn‖=0;
limn→∞‖yn-un‖
=limn→∞(1-μn)‖Jrn(un+en)-un‖
≤limn→∞(1-μn)‖Jrn(un+en)-un-en‖+
limn→∞(1-μn)‖en‖=0。
进一步,得
limn→∞‖yn-Jrnyn‖≤limn→∞(‖yn-un‖+
‖un-xn‖+‖xn-xn+1‖+‖xn+1-Jrnyn‖)
和
limn→∞‖xn-yn‖≤limn→∞(‖xn-un‖+
‖un-yn‖)
即有
limn→∞‖yn-Jrnyn‖=0;limn→∞‖xn-yn‖=0
(9)
第五步证明limn→∞‖yn-Jrxn‖=0。
由引理1可知
‖yn-Jryn‖≤‖yn-Jrnyn‖+‖Jrnyn-Jryn‖
‖yn-Jrnyn‖
根据(9)式和条件limn→∞rn=r,有
limn→∞‖yn-Jryn‖=0
(10)
另外
‖xn-Jrxn‖≤‖xn-yn‖+‖yn-Jryn‖+
‖Jryn-Jrxn‖
≤2‖xn-yn‖+‖yn-Jryn‖
结合(9)式和(10)式,可知
limn→∞‖xn-Jrxn‖=0
(11)
第六步证明limn→∞sup〈p-f(p),j(p-xn)〉≤0。
设xt=tf(xt)+(1-t)Jrxt,由引理5知,{xt}强收敛到p,也是(2)式的唯一解。对∀t∈(0,1),有
‖xt-xn‖2=t〈f(xt)-xt+xt-xn,j(xt-xn)〉+
(1-t)〈Jrxt-Jrxn+Jrxn-xn,j(xt-xn)〉
≤t‖xt-xn‖2+t〈f(xt)-xt,j(xt-xn)〉+
(1-t)‖xt-xn‖2+
(1-t)〈Jrxn-xn,j(xt-xn)〉
≤‖xt-xn‖2+t〈f(xt)-xt,j(xt-xn)〉+
(1-t)‖Jrxn-xn‖‖xt-xn‖
移项整理得
〈xt-f(xt),j(xt-xn)〉
根据第一步结果和(11)式,得
limn→∞sup〈xt-f(xt),J(xt-xn)〉≤0。
注意到,当t→0+时,xt→p,
|〈p-f(p),j(p-xn)〉-〈xt-f(xt),j(xt-xn)〉|
≤|〈p-f(p),j(p-xn)〉-
〈p-f(p),j(xt-xn)〉|+
|〈p-f(p),j(xt-xn)〉-
〈xt-f(xt),j(xt-xn)〉|
≤‖p-f(p)-xt+f(xt)‖‖xt-xn‖+
‖p-f(p)‖‖p-xt‖→0,t→0+
∀ε>0,∃δ>0,对∀t∈(0,δ),有
〈p-f(p),j(p-xn)〉
≤〈xt-f(xt),j(xt-xn)〉+ε
易得
lim supn→∞〈p-f(p),j(p-xn)〉
≤lim supn→∞〈xt-f(xt),j(xt-xn)〉+ε
由ε的任意性,有
lim supn→∞〈p-f(p),j(p-xn)〉≤0
即
lim supn→∞〈p-f(p),j(p-xn+1)〉≤0
(12)
第七步证明当n→∞时,xn→p。
‖xn+1-p‖2=αn〈f(yn)-p,j(xn+1-p)〉+
(1-αn)〈Jrnyn-p,j(xn+1-p)〉
≤(1-αn)‖yn-p‖‖xn+1-p‖+αnρ‖yn-p‖·
‖xn+1-p‖+αn〈f(p)-p,j(xn+1-p)〉
αn〈f(p)-p,j(xn+1-p)〉
≤αn〈f(p)-p,j(xn+1-p)〉+
(δn‖xn-p‖+(1-δn)‖xn+1-p‖+
‖en‖)2]
=αn〈f(p)-p,j(xn+1-p)〉+
‖xn+1-p‖2+(1-δn)2‖xn+1-p‖2+
2δn‖xn-p‖‖en‖+2δn(1-δn)‖xn-
p‖‖xn+1-p‖+2(1-δn)‖xn+1-p‖‖en‖]
‖en‖(‖en‖+2δn‖xn-p‖+2(1-
δn)‖xn+1-p‖)+(2-δn)‖xn+1-p‖2]+
αn〈f(p)-p,j(xn+1-p)〉
这表明

2δn‖xn-p‖+2(1-δn)‖xn+1-p‖]+
令
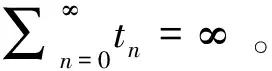
令

令
2δn‖xn-p‖+2(1-δn)‖xn+1-p‖]
已知ρ∈ [0,1),αn∈(0,1)和0<δ≤δn<1,有
2-[1-αn(1-ρ)](2-δn)>2-2+δn>δ,
进一步有
cn<
p‖]
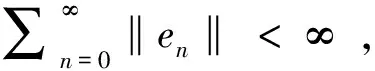
推论1设E是自反的一致凸Banach空间,具有一致G-微分范数。C是E中的非空闭凸子集,且具有正规结构。令f:C→C是压缩映像,压缩系数ρ∈[0,1)。A是E中的m-增生算子且N(A)≠∅。对于任一x0∈C,∀n∈N,序列{xn}由下式生成
若{αn},{μn}和{rn}⊂(0,1),{en}⊂E,满足如下条件:
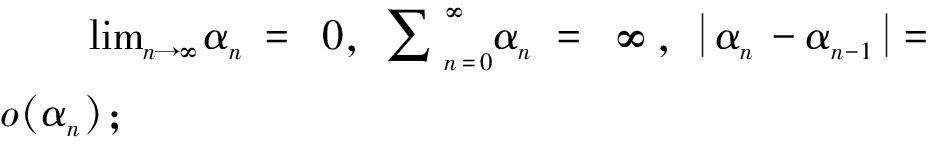

那么序列{xn}强收敛于一点p∈N(A),也是变分不等式问题(2)的解。
推论2设E是自反的一致凸Banach空间,具有一致G-微分范数。C是E中的非空闭凸子集,且具有正规结构。令f:C→C是压缩映像,压缩系数ρ∈[0,1)。A是E中的m-增生算子且N(A)≠∅。对于任一x0∈C,∀n∈N,序列{xn}由下式生成
若{αn},{δn},{μn}和{rn}⊂(0,1),满足如下条件:
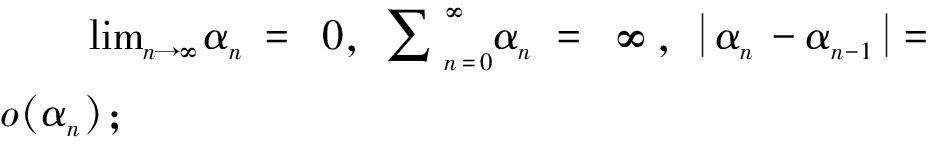

那么序列{xn}强收敛于一点p∈N(A),也是变分不等式问题(2)的解。
