具有输入饱和约束的周期多智能体系统的双边一致性 *

何冬燕，谢玮玮，杨新荣

（广西师范大学 数学与统计学院，广西 桂林 541004）

0 引言

众所周知，多智能体系统的集群性行为已在生物学、物理学、计算机科学和控制工程等领域有了相应的研究结果。例如，多机器人系统、无人机、编队控制［1］、群集［2-3］和卫星群［4］的姿态对准衔接等等。在现有研究中，主要有智能体的协作或竞争性行为，针对这两种行为，常用符号图来描述智能体之间的合作或竞争关系。［1-7］利用符号有向图描述多智能体系统，可以将其用于考虑各种动态性行为的研究。［5-7］基于符号网络图的描述，如何将智能体的最终状态达到一致性是研究者比较关注的问题，主要应用在无线传感器网络中的时钟同步、自主智能体的交会和无人驾驶飞行器的编队控制等领域。

在系统满足渐近零可控且有界控制的条件下，［8］低增益反馈技术是实现半全局渐近镇定的有效方法。该方法也被用来处理多智能体系统的半全局一致性问题。［15-16］利用低增益反馈技术以及李雅普诺夫函数方法，文献［15］和［16］分别在有向网络拓扑图和无向网络拓扑图框架下研究了存在饱和约束的线性多智能体系统的半全局一致性问题。基于以上文献所得结果，文献［7］首次给出了类拉普拉斯反馈控制律使得多智能体系统达到半全局双边一致。但文献［7］只考虑了具有定常系数矩阵的系统，并没有考虑具有周期系数矩阵系统。然而在现实世界中，具有周期动力学的多智能体系统却应用于很多领域中，例如，机器人系统、卫星网络或飞机编队控制等领域。由此可见，周期性多智能体系统是一类非常重要的系统，从而吸引了许多研究者对其进行研究。［9-12］综上所述，关于周期多智能体系统的双边一致性研究相对较少。因此，对周期动力系统作进一步深入研究是十分必要的。

本文所采用以下记号：用ℓ(A(t)) 表示矩阵A(t) 的特征乘子。令C∘={z：|z| ＜1 }，C⊕={z：|z| ≤1 } 以及C•={z：|z|= 1 }，则C⊕=C∘∪C•。

1 问题阐述与预备知识

1.1 符号图的基本知识

设N阶加权无符号/符号有向图G={V，ε，Aa}，其中V={ 1，2，…，N}为节点集，ε⊆V×V为边集，Aa=[aij]∈RN×N是描述边信息的关联邻接矩阵。非零元素aij依附在边(i，j)∈ε上。(i，j)∈ε表示从节点j到节点i存在有向边，并规定aii= 0，∀i= 1，2，…，N。如果aij≠0，则aij＜0 或aij＞0。正/负权重aij表示相邻连接的两个智能体存在合作/竞争关系。L(G)=L=[lij]∈RN×N表示拉普拉斯矩阵，如果i≠j，则lij=-aij，否则lij=在符号有向图中，G的有向路径是一系列边(i1，i2)，(i2，i3)，…，(il-1，il)，其中所有节点i1，i2，…，il互不相同。如果有向图G中有两个不同的节点连接到有向路径上，则称有向图是强连通的。

1.2 问题描述

考虑以下2π周期多智能体系统的双边一致性问题：

其中A(t)：R→Rn×n，B(t)：R→Rn×m分别为系统矩阵和控制矩阵。xi(t)∈Rn表示智能体i的状态，ui(t)∈Rm表示作用于智能体i上的控制输入，sat：Rm→Rm表示饱和函数sat(ui)=[ sat(ui1)，…，sat(uim) ]T。对于给定的系统（1），找到类拉普拉斯反馈控制律

使得闭环多智能体系统

达到半全局双边一致，其中K(t)∈Rm×n是待定的增益矩阵，aij表示与底层拓扑图有关的邻接矩阵Aa的第(i，j)个元素。

1.3 符号图的相关知识

任意N阶无符有向图G，Gi，i= 1，2，…，q(1 ≤q≤m)，当Gi不仅是G的极大子图，而且是强连通时，称Gi为G的强连通分部。不失一般性，假设Gi，i= 1，2，…，q(1 ≤q≤m) 是G的强连通分部，每个强连通分量有nl，l= 1，2，…，q个节点。此外，G的拉普拉斯矩具有以下Frobenius 结构：

定义1［7］RN正交阶规范变换由D= diag {l1，l2，…，lN} 作用而来，其中li∈{-1，+ 1 }。经过规范变换后，若li≠lj，则矩阵元素符号将发生改变，否则保持不变。定义是RN中所有规范变换的集合。

定义2［7］如果对于任意给定的有界集X⊂Rn，可以计算出一个增益矩阵K(t)，使得对任意的i，j=1，2，…，N，只要xi( 0 )∈X，且则周期多智能体系统（1）可达到半全局双边一致。

引理1［7］给定任意一个具有有向生成树的无符有向图G，设是与G相关联的拉普拉斯矩阵，具有Frobenius 范式。定义其中δi，i= 2，…，q是任意标量。对于任意y∈RN，且满足则下列不等式成立：

其中

如果G1只包含G的根节点，意味着那么Q可以是任何正数；否则，其中为有向图G1的代数连通性，定义为

2 主要结果

假设1矩阵对(A(t)，B(t))是可控的，且矩阵A(t)满足ℓ(A(t))⊂C•。

定理1若系统（1）满足假设1 且底层拓扑图是具有有向生成树的结构平衡图［5］，则可设计增益矩阵K(t)使得反馈控制定律（2）实现系统（1）的半全局双边一致。

由文献［13］可知P(t，γ)随γ单调递增且。因此，选取γ足够小，使得

进一步简化得：

意味着

其中P(t)=P(t，γ)。因此，ei(t)，i= 1，2，…，N以指数速率趋于0。意味着

其中= 1，所以系统（1）可以达到半全局双边一致。因此，

又P(t，γ)随着γ的增大而增大。因此，可以选择γ足够小，使得

对于xi( 0 )∈X，i= 1，2，…，N，则

即不等式（6）是满足的。因此定理1 证毕。

3 例子验证

下面通过文献［8］中的例子说明本文所得结果的有效性。

考虑2π周期系统（1），其系数矩阵A(t)，B(t)由如下矩阵给出，并选取ω= 4。

系统的状态转移矩阵记为：

由此可计算出矩阵A(t)的特征乘子集为l(A(t))={ 1，1，1 }，因此，假设1 是成立的。

可选取γ= 0.27，β= 0.6，δ2= 0.8，δ3= 0.6，由此计算出文献［8］中方程（11）的唯一对称正定解为：

其中

考虑如图1 所示的有向拓扑图。由图1 可知，拓扑图共有6 个节点且含有有向生成树。其中，虚线/实线分别表示智能体竞争/合作关系。又由强连通分部及结构平衡的定义，节点可分为两个子节点集V1={ 1，4，5，6 }和V2={ 2，3 }，因此，符号图G的拉普拉斯矩阵L可表示为：

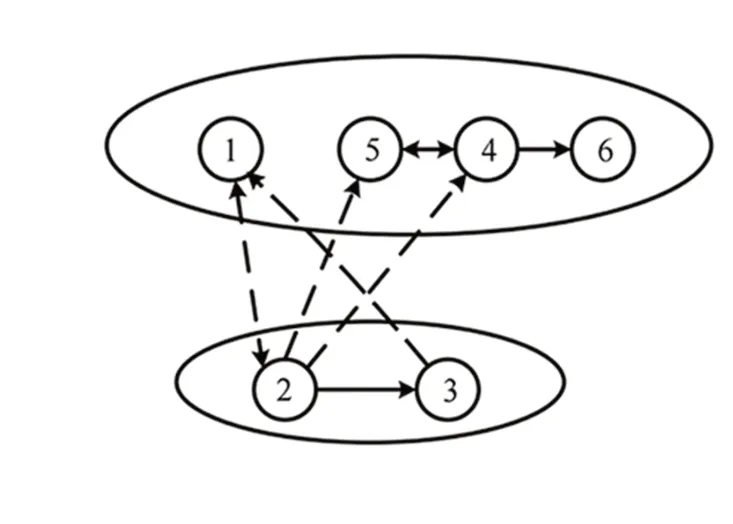
图1 6 个智能体的网络拓扑图

由图2～图4 可以看出，智能体1、4、5、6 和智能体2、3 的大小相等，符号相反。误差状态轨迹如图5 所示，可以看出所有智能体的误差状态最终趋于零。由图6 可知，多智能体系统的饱和控制输入ui(t) 均小于饱和值ω= 4。综上所述，基于设计的类拉普拉斯反馈控制律，实现了周期系统的半全局双边一致。

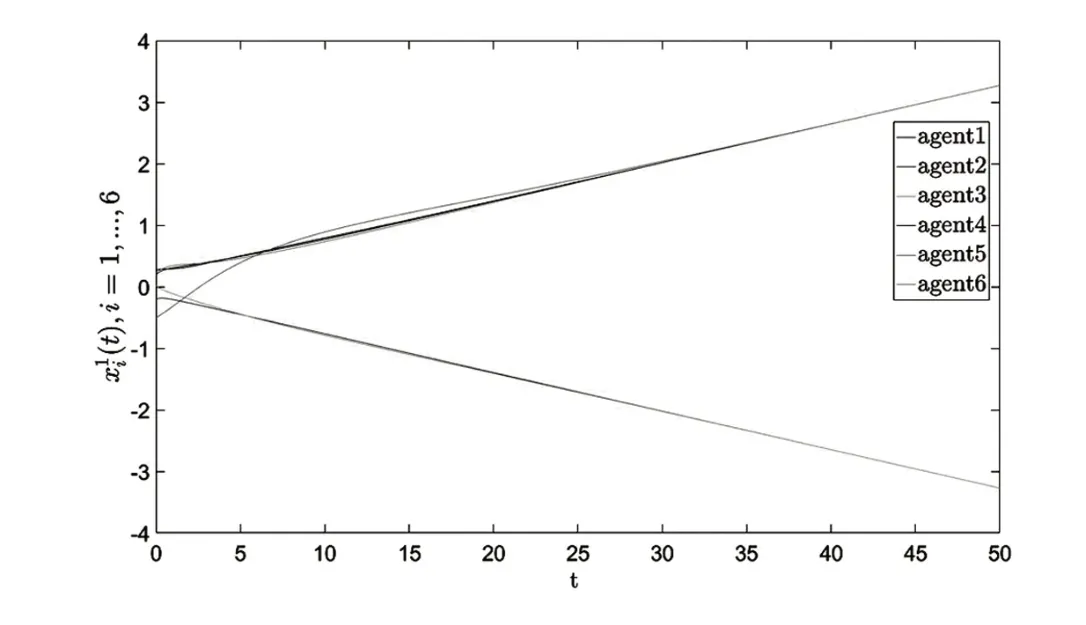
图2 智能体状态 = 1,…,6 轨迹图

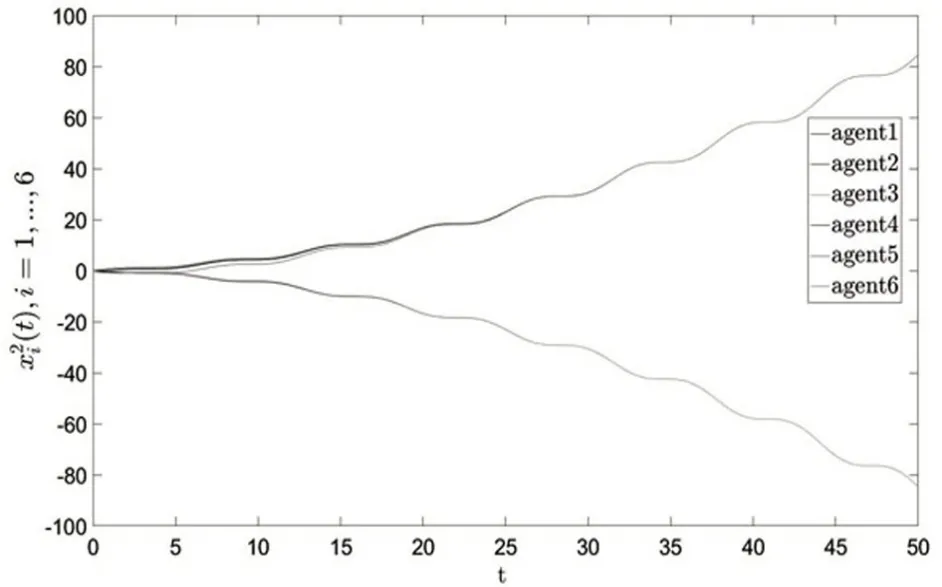
图3 智能体状态,i = 1,…,6 轨迹图

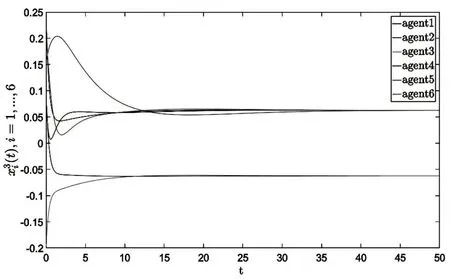
图4 智能体状态,i = 1,…,6 轨迹图

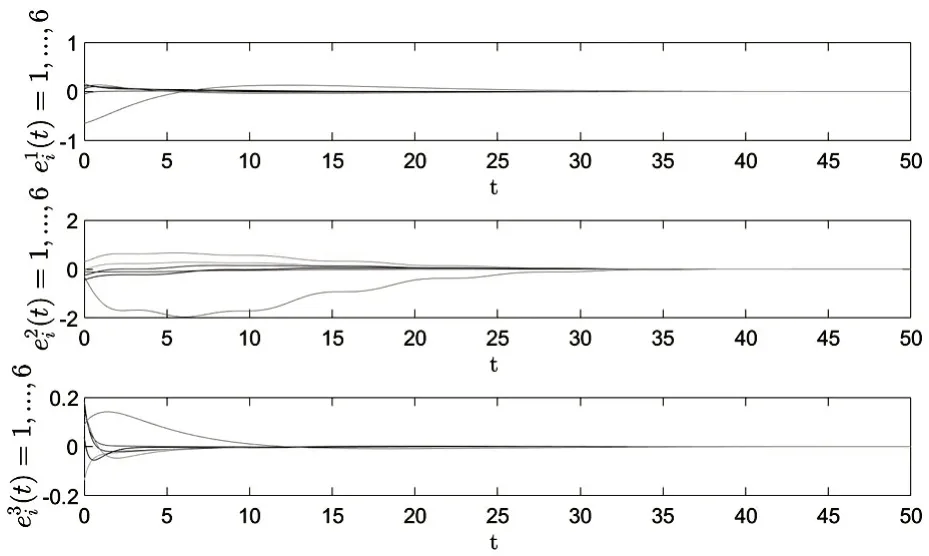
图5 智能体误差状态轨迹图

图6 控制ui ( t ),i = 1,…,6

4 结语

本文主要研究了具有饱和约束的周期多智能体系统的半全局双边一致性问题。给出了类拉普拉斯反馈控制律，实现了周期系统的半全局双边一致。利用李雅普诺夫函数的方法，分析了该算法的收敛速度。并通过算例说明了所得结果的有效性。