基于改进型蚁群算法的路径优化仿真实验
2023-05-22汪伦杰王棪
汪伦杰,王棪
(1.贵州大学 现代制造技术教育部重点实验室,贵州 贵阳 552200;2.贵州大学 机械工程学院,贵州 贵阳 552200)
0 引言
路径优化即路径规划问题,在行李分拣系统中,路径优化是提高分拣效率的关键。在给定的传输网络中,以行李的出发点和终点作为输入,以传输带速度等作为约束条件,通过一定的算法得到满足条件的最优输送路径,是路径优化的主要内容[1-3]。根据实际需求的不同,所采用的优化标准也各不相同,例如距离最短路径、时间最短路径、拥挤级别最低路径、可靠性最大路径等。路径优化的核心问题即图论中的最短路问题[4-6]。
在行李输送的过程中,由于行李本身属性的差异性,导致不能按照单一的标准进行最优路径选择。例如针对易碎行李,在保证输送效率最高的同时还要保证该路径的平稳性。对于危险系数较高的行李,首先要满足的是三级安检的正常进行,而不是输送速度的最优,特别是某些需要人工进行开包的行李,尤其要避免其在输送过程中被剧烈地碰撞和颠簸。行李与旅客所乘坐航班的信息是一一对应的,对于值机延迟的旅客,在保证行李顺利安检的同时,如何保证行李与旅客的同步性尤为重要,这就要求行李在输送过程中时间最短,保证该行李的及时装机,同时能够区别于其他行李而被单独对待。诸如此类特殊属性是行李输送系统中经常需要关注的,该类信息对于最优路径选取的影响不容忽视[7,8]。
1 传统蚁群算法的局限性
在利用蚁群算法[9,10]寻求最优输送路径时,一般将蚂蚁看作行李托盘。蚂蚁依据路径选择策略对行李进行选择,否则就返回仓库,进入下一轮的选择。如果蚂蚁完成了范围内所有行李的选择,算法对每一只蚂蚁所构建的路径进行计算,并对信息素进行更新,得到一次的迭代结果。多次的迭代可以得到一个优化解。相比于其他智能算法,蚁群算法在最优路径选择方面具有较高的优势,但是仍有其局限性。
初始行李的选取将直接影响最优路径的求解,这是因为蚂蚁和行李具有双重负载要求,蚂蚁的活动具有访问数量和顺序的问题。传统的基于蚁群算法的最优路径选取算法,都是以与蚂蚁初始位置相连的节点为关键节点的,当行李处于非关键节点时,蚂蚁走不出理想的最优路径。
2 改进型蚁群算法
2.1 蚂蚁位置初始化
初始化方式可描述如下:将所有蚂蚁置于托盘集散中心,在t时刻,将时间距离信息按照组合优化选择模型生成初级最优路径。初始行李选择可表示为:
其中,allow(0)蚂蚁处于集散中心的初始位置。设定q为[0~1],设定q0为[0.8~0.95]。蚂蚁位置的初始化是最优与随机选择的结合,蚂蚁会选择与自身信息素关联度最高的行李作为待处理对象。随着算法迭代次数的增多,路径上信息素的正反馈增强,蚂蚁将被引导到关键节点附近对待处理行李进行搜索。
2.2 路径选择方式
在蚁群系统(Ant Colony System,ACS)中,启发因子ηij可定义为蚂蚁当前位置i与目标(待处理行李或者滑槽)位置j之间距离dij的倒数,可表示为:
当蚂蚁k在t时刻的位置为i,目标位置为j,可得路径选择公式为:
其中:allow(i)表示蚂蚁在当前位置i的目标位置集;q为random(0,1),q0设定为[0.8~0.95];蚂蚁k处于位置i时选择目标j的概率可表示为为信息影响因子。该种路径选择策略使蚂蚁以较大概率q0向信息素与η乘积最大的待处理目标移动。这将使以随机原则选择的目标位置所占比例减少。在保证蚂蚁路径选择的方向性的同时,增加搜索选择的多样性。
2.3 信息素更新及限制
每次迭代结束,规定只有本次最优解或者全局最优解集合中的路径所对应信息素会增加,其他路径信息素因挥发而减少。即信息素的更新为局部更新和全局更新的结合,可表示为:
为避免算法的过早收敛,需要对信息素的浓度做出限制。用τmax和τmin分别表示信息素的上限值和下限值。每次迭代结束,需要算出各个路径新的信息素浓度,并根据以下调整准则进行调整。
τmax、τmin分别定义为:
其中:ρ表示信息素挥发系数;Lgb代表全局最优解长度。在收敛状态下,Pbest>0.5 对寻求最优解更有利。
2.4 算法步骤
改进蚁群算法步骤如下:
步骤一:基于多准则路径优化选择模型进行初始路径选择。确定出发点S和终点E,基于有向图模型G=(V,E,W),确定路径所有节点集合V和路径集合E,计算距离最短模型。由路径行李密度Qij计算道路饱和度K,综合单件行李安检时间和行程时间,得到时间最短路径选择模型。依据航班信息确定距离和时间的权重系数ωc、ωd。由公式(9)得到初始最优路径。
步骤二:蚁群算法初始化。按照目前的行李最优路径,设置迭代次数N、路径长度L以及迭代次数上限T;将e个托盘从周边仓库中调出,并将托盘与行李一一对应起来,计算行李路径之间的关联度ηij及信息素初始值τ0。初始化每个托盘的禁忌表tk(k=1,2,...,e),由路径长度lek和负载量lok得到路径上的信息素τij。
步骤三:信息素局部更新。托盘按照负载条件进行路径规划,每走过一段路径就按照式(4)进行信息素局部更新。
步骤四:返回仓库。如果托盘完成一次运输,则回到最近仓库,并将仓库号添加到禁忌表tk,更新lek和lok。
步骤五:2-opt 搜索。当所有托盘路径构建完毕后,就对该路径进行2-opt 搜索并更新lek、tk,否则回到步骤三。
步骤六:优化初始值。算法经过N次迭代,最优路径不再变化,则对lek与S进行比较。当lek<S时,t=tk,用较短的lek替换掉算法初始化时的S,并对信息素进行更新;如果相同,则进行交换搜索并更新信息素。
步骤七:循环条件。当迭代次数N≤T,则返回步骤二,否则算法结束并输出最优解。
3 基于改进蚁群算法的行李传输路径仿真实验
在行李管理系统中,出于安全出行的考虑,对每件行李最多要进行5 级安检。首先是X 光机进行1 级安检,对行李进行扫描,并将扫描结果以透视图方式发送至2 级安检进行判读。如果行李判读安全,则直接进入行李分拣转盘进行滑槽匹配分拣;如果有疑问,则传输至第3 级CT 机进行检查,经过CT 机检测通过的进入行李分拣转盘;没有通过的进入第4 级EDT 设备进行检测,检测通过的在行李分拣转盘进行分拣;没有通过检测的进入5 级人工开包间进行开包处理。
为了得到行李传输的最优路径,需要综合行李自身特殊属性、航班信息、行李实时定位信息及分拣传输设备运行情况等多方面信息。系统架构如图1所示。

图1 行李传输系统
以某机场行李分拣系统为参考,在舍去2 级和4 级安检的条件下,对行李传输系统进行场景结构搭建。在系统中设置了4 组值机岛,一级安检设备8 套,3 级安检CT 机4 台,行李分拣转盘4 个,行李托盘库4 个,在最后设定了4 个5级安检人工开包间。
为了验证该仿真实验,在系统入口界面进行相关设置,按照不同行李要求,将路径选择标准定为距离最短、时间最短以及转角最少。将三种运算结果同时显示出来,以方便比较。
云平台所接入对象为某机场历年行李业务数据经挖掘清洗处理后的月平均客流量信息,以及该月内行李实时定位数据镜像。该云平台实现了对航班信息、行李信息以及旅客信息的集成化处理。云平台接口的实现,可以使本行李传输路径仿真系统在最大可能条件下实现与真实行李传输工况的统一。为了降低仿真所耗资源,将DCV 数量设定为30,行李属性为普通属性,即不具备易碎、防压、防倾覆等特殊属性。
实验结果如图2所示。可见基于最短路径标准的路径1 与基于最少转角的路径2 相比,总路程长度相差3.1 m,时间差为47 s,但是转角数差值则为8。这说明即使在距离和时间相差不大的情况下,不同的路径选择标准下所得到的解在转角数上会有大的差别;基于时间最短标准所得到的路径3,行程距离比路径1 和路径2 都要长,且差距较大,平均差距为64.4 m,但是输送时间却比路径1 和路径2 要短很多。经计算可得,路径1 和路径2 的平均传送速度为0.78 m/s,路径3 传输速度为1.56 m/s。
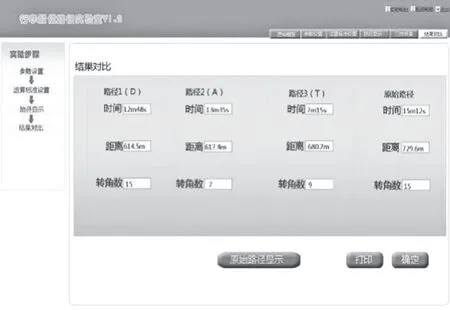
图2 实验结果
通过对原始路径信息的分析可以发现,在当前运行机制中,设定了行李托运值机柜台与滑槽的对应关系,这就要求旅客依据提示到指定柜台办理托运。如果在其他柜台办理托运,行李不是直接被输送至滑槽处,而是需要先按照最短路径被传输至相应值机岛,再被分配到该值机岛所对应的行李传送路径。由结果可得,平均传送速度为0.80 m/s,传送路径全长729.6 m,通过转角数为15。以上数据是在系统设计最低压力下的理想结果。
由仿真实验可得,基于蚁群算法的最优路径计算是根据动态路径以及行李实时定位等信息,并结合航班信息来判断行李路径选择标准的,最后根据该标准为行李选择最优路径。该方法在提高行李服务质量的同时,也实现了对行李传输系统资源的合理分配和有效利用。
4 结语
本文以影响行李输送的多方面因素为输入,以模糊理论为依托,得到了基于时间和距离约束的行李分拣系统的最优路径选择模型;同时结合蚁群算法对路径优化算法进行了改进,最后通过实验验证了本文算法的合理性和有效性。
