基于改进型粒子群算法的栽植机四杆机构优化设计
2023-05-20李盼
李 盼
(湖南城建职业技术学院,411101,湖南湘潭)
平面四杆机构作为多杆机构的基础,应用十分广泛,在众多工农业机械和工程机械中得到了广泛的应用,在栽植机中也都用到了四杆机构[1]。
对于栽植机四杆机构的设计,传统设计方法采用的是作图法与解析法[2]。这些方法只能按照少数精确点进行设计,更难以同时兼顾其他性能指标,其设计精度和效率不能够满足现代机械的需求。因此,国内外学者针对栽植机四杆机构优化设计问题,在受力分析、轨迹优化等各方面进行了相关研究[3-5]。这些方法都有较好的设计结果,但是需要额外的设计数理知识。因此,智能优化算法被应用于栽植机四杆机构的优化设计[6-8]。
本文针对栽植机四杆机构设计问题,提出了一种基于改进型粒子群算法的优化设计方法。首先,以栽植机四杆机构为研究对象,建立了以机构输出角的平方偏差最小化的优化模型。其次,提出了一种改进型粒子群算法,通过引入非线性的动态惯性权值系数,平衡粒子群的局部改良能力与全局搜索能力。最后,将所用方法应用于栽植机四杆机构的优化设计,并与复合形法、约束随机方向法的优化设计结果进行比较,发现设计结果有了明显优化,验证了该改进型粒子群算法更适用于栽植机四杆机构的优化设计。
1 数学模型
栽植机四杆机构简化图如图1 所示。其中,ABCD为平面四杆机构,A、B、C、D 分别为不同的铰链,AB 为曲柄,AD 为机架,BC 和CD 分别为连杆和摇杆。B'、C'为该平面四杆机构在右侧极限位置时B、C 的位置。当原动件曲柄AB 的转角φ=φ0~(φ0+90°)时,要求从动件摇杆的输出角能够满足函数(φ-φ0)2,其中φ0、Ψ0分别为右侧极限位置时曲柄AB 和摇杆CD 的初始位置角。以机架AD 方向的逆时针作为标准方向,则机构传动角范围应满足条件:45°≤γ≤135°。取曲柄长度为单位长度l1=1,则机架相对长度l4=5。
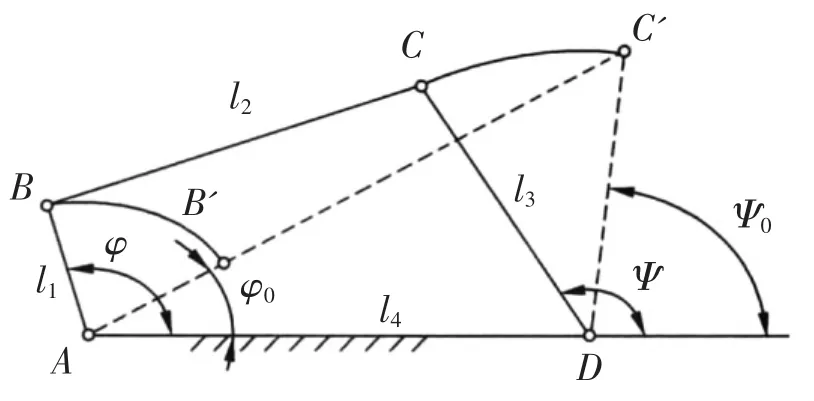
图1 栽植机四杆机构简化图
1.1 设计变量
根据图1 所示,该平面四杆机构按照原动件和从动件角度对应关系,有5 个独立参数:连杆长度、摇杆长度、机架杆长度、曲柄的初始角和摇杆的初始角。按照图1 所示,可以根据平面四杆机构确定φ0、Ψ0在极限位置时的运动几何关系:
因此,可以得到设计变量为:
1.2 目标函数
优化设计的目标是使得实际的输出角尽可能与期望输出角相同,可以理解为机构的输出角的平方偏差最小,因此目标函数为:
式中:Ψsi为期望输出角,s 为离散点数,i 为各离散点的序号。
根据图2 所示,可以由机构的运动几何关系确定期望输出角的表达式,即
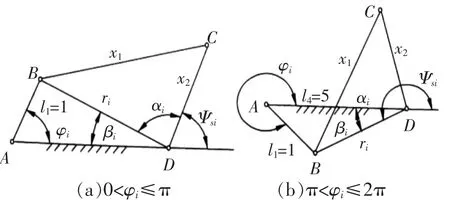
图2 机构的输入角与输出角关系
式中αi和βi,可以根据几何关系得到:
1.3 约束条件
(1)传动角约束条件。为了保证机构具有良好的传力性能,对于该平面四杆机构,其最小传动角要满足要求γmin≥45°或最大传动角满足要求γmax≤135°。
根据图3 所示,平面四杆机构具有最小传动角或最大传动角时,曲柄AB 恰好与机架AD 共线,因此可以得到:

图3 机构的传动角极值
即可得到约束方程:
(2)杆长约束条件。根据平面四杆机构中曲柄存在的杆长之和条件,可以得到约束方程:
根据上述约束条件,绘制出与约束条件相关联的设计平面,得到图4。从图4 可知,杆长相关的约束条件对于该优化设计问题来说,属于无作用约束,不组成该模型求解的可行域。

图4 约束条件的设计平面
综上所述,可以得到该优化设计问题的数学模型为:
2 改进型粒子群算法
传统的设计方法主要采用的是作图法或解析法,该设计方法不仅耗时长、效率低,而且所得到的设计结果有时候也难尽如人意。因此,为了提升优化设计的精度和效率,采用了一种群智能优化算法,即自适应权值粒子群算法(APSO),根据上述建立的相关数学模型,对栽植机四杆机构进行优化设计。
2.1 自适应权值粒子群算法(APSO)
粒子群算法(PSO)的主要思想是将微粒群的运动近似于鸟类的飞行,通过粒子群之间的协作与信息共享来求解复杂的优化问题,即
为了更好地对微粒的飞行速度进行控制与调整,引入了惯性权重系数,同时为了避免粒子群陷入局部极值、早熟等现象,平衡粒子群的局部改良能力与全局搜索能力,采用非线性的动态惯性权值系数,该算法亦称为自适应权值粒子群算法,即
2.2 外点惩罚函数法
平面四杆机构优化设计问题属于约束非线性规划问题,采用直接解法的难度大且难以得到良好结果,因此为了更好求解该类问题,本文所采用的是外点惩罚函数法,即
3 平面四杆机构优化结果
针对该优化设计问题,采取复合形法、约束随机方向法和自适应权值粒子群算法分别进行优化设计,对比不同优化方法所得到的优化结果并进行分析。
3.1 利用复合形法进行设计
复合形法是指在n 维设计空间的可行域内,对复合形的各顶点的目标函数值逐一进行比较,不断取点最坏点,代之以既能使目标函数值有所下降,又能够满足所有约束条件的新点,逐步调向最优点。
由于该栽植机四杆机构设计问题从数学模型可知,是一个二维非线性优化设计,因此可以直接在可行域内选择K 个顶点,构成初始复合形,即:
利用Matlab 软件进行计算,其计算结果如图5 所示。

图5 复合形法计算结果
3.2 利用约束随机方向法进行设计
利用Matlab 中的rand(m,n)函数,产生一个一行两列的随机函数,将[0,1]区间内均布的伪随机数列{ri}转换成(-1,1)区间内均匀分布的随机数列{yi},在可行域内人为选择一个初始点,然后生成随机方向,生成新点;检验该新点的可行性与适用性,如该新点满足终止条件,则输出最优点和最优值;反之,继续计算,直至满足终止条件。
利用Matlab 软件进行计算,其计算结果如图6 所示,适应度曲线如图7 所示。

图6 随机方向法计算结果
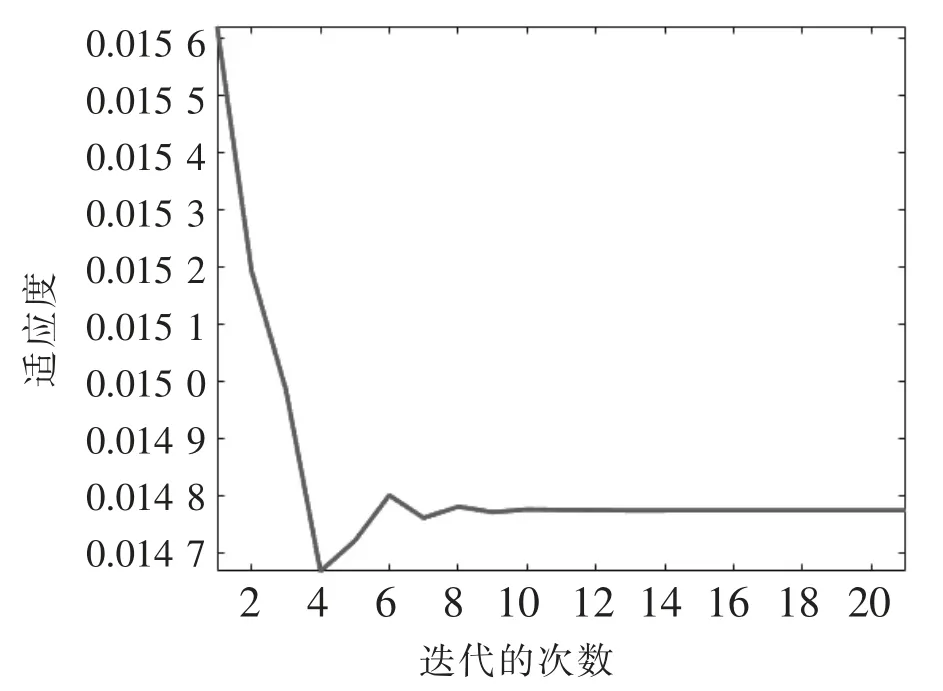
图7 随机方向法适应度曲线
3.3 利用自适应权值粒子群算法进行设计
设置自适应权值粒子群算法的计算参数,粒子群数为100,最大迭代次数为1 000,惯性权值系数为0.729 8,学习因子均为1.496 18。
利用Matlab 软件进行计算,其计算结果如图8 所示,适应度曲线如图9所示。从图9 可知,自适应权值粒子群算法反映了比较好的鲁棒性和适应性。

图8 APSO 计算结果

图9 APSO 适应度曲线
对比复合形法、约束随机方向法和自适应权值粒子群算法的计算结果,得到表1。从表1 可知,APSO 的计算结果明显好于其余方法的结果,且具有良好的全局收敛性和收敛速度,因此可以认为APSO 在平面四杆机构优化设计方面具有可行性和正确性。

表1 不同算法计算结果对比表
4 结语
针对栽植机四杆机构设计问题,提出了一种基于改进型粒子群算法的优化设计方法,得到了以下结论。
(1)传统的经验设计所得到的结果往往不尽如人意,为了提高设计的精度和效率,采用智能优化算法(APSO)对其进行优化设计。
(2)采用APSO 的计算结果明显好于复合形法和随机方向法的结果,且具有良好的全局收敛性和收敛速度。
(3)智能优化算法相比于常规设计方法,避免了经验设计的盲目性,对于栽植机四杆机构的优化设计具有良好的指导意义。
