基于等维灰数递补GM(1,1)与发展带模型的我国安全生产事故预测研究

刘 伟,张丽丽

(华北科技学院 经济管理学院,北京 东燕郊 065201)

0 引言

当前,安全生产和安全发展已成为全社会关注的焦点问题。准确地预测安全生产事故相关数据,有利于做好安全生产事故预防工作,进而提高我国整体的安全生产水平。

由于使用单一模型预测存在一定局限性,国内外学者使用多种模型或将单一模型进行组合,建立集成预测模型,通过不同模型之间的优势互补提高预测效果。如龙会典、严广乐[1]于2017年构建了一个动态GM(1,1)-Markov链组合预测模型,以1991-2014年广东省单位GDP能耗数据实证了该模型的预测效果;Wedding等[2]于1996年建立了由模型与神经网络组合成的时间序列集成预测模型;Aslanargun等[3]于2007年对旅游需求建立季节模型与神经网络集成的预测模型,并在此基础上比较了组合模型与单一模型的预测效果。研究结果表明：多种预测方法的效果要好于单一预测。

灰色预测法是邓聚龙教授灰色系统理论中提出的预测方法[4]。灰色系统理论以“部分信息已知,部分信息未知”“小数据”“贫信息”“不确定性”系统为研究对象[5]。对于传统GM(1,1)模型而言,如果原始序列本身光滑度不高,或者存在某些极端值,就会严重影响模型的预测精度。因此,模型的初始值、背景值和参数估计方法等是影响 GM(1,1) 模型的预测精度的常见因素[6]。为了提高GM(1,1)模型的预测精度,可通过选取相关建模数据弱化算子的变换方法来实现[7]。针对小样本序列预测问题,灰色预测模型通过序列运算算子弱化原始序列的随机性,提高光滑性构建具有部分微分、部分差分性质的模型,以揭示行为系统的发展趋势[8]。目前,灰色预测模型已经成为处理不确定系统的一种有效方法,在交通[9]、能源[10]、水文[11]等领域取得了广泛应用。

通过梳理文献发现基于灰数GM(1,1)模型对我国各类安全生产事故进行预测的文章尚属空白。因此,本文基于事故数据等维灰数递补GM(1,1)模型和发展带区间预测模型,对2021-2025年我国安全生产事故数据进行了点预测(递推值和基础值)和区间上下界预测,为安全应急管理工作和制定安全发展政策提供基础数据支撑,并针对安全事故预防工作提出了对策与建议。

1 理论模型设计与步骤

1.1 等维灰数递补模型与发展带理论

灰色理论认为,系统历史信息对研究系统有一定的作用,但与预测时间更接近时期中的信息对研究系统的特殊性更有价值。这是由于随时间的推移,未来的一些扰动因素将不断进入系统而对系统施加影响。因此,GM(1,1)模型虽可以进行长期预测,但是从灰平面上看,真正具有实际意义且精度较高的预测值,仅是最近的一、二期数据,其他远期的预测数据仅反映一个趋势[12]。而我国统计数据通常滞后一年以上,影响了改善生产系统结构的决策行为。而等维灰数递补GM(1,1)模型是一种动态模型,它先用已知数据生成原始数列,建立GM(1,1)模型预测一个值,将其补充至已知数列中,同时去掉第一个已知数据,使序列等维再建立GM(1,1)模型,再预测下一个数值,并补充到数据列中,同时去掉最老的一个数据……,如此循环,用预测灰数新陈代谢逐个预测,依次递补完成预测,直到完成预测目标或达到要求的预测精度为止,预测精度比静态GM(1,1)模型有显著提高[13]。

无论静态GM(1,1)模型还是动态GM(1,1)模型,预测值都是点预测,有时我们需要认识行为系统未来数据变化的数据范围,而发展带反映式则预测出系统未来数据变化取值区间,实现了从点预测到区间预测的拓展,具有重要现实指导意义。

1.2 建模事先检验

设原始序列为x(0),建立高精度GM(1,1)预测模型之前需作事先检验,满足以下检验：

(1)x(0)的级比检验

(2)x(0)的准光滑性检验

若以上检验均通过,则表明序列满足GM(1,1)模型的建模条件,适合建立GM(1,1)模型[5]。

1.3 GM(1,1)模型建模

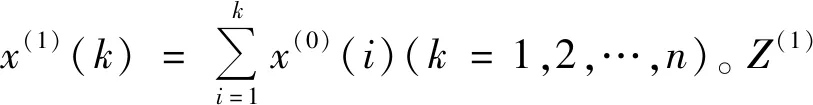
则GM(1,1)灰微分方程对应的白化微分方程为：

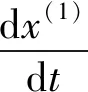
(1)

求解微分方程,可得到预测模型：

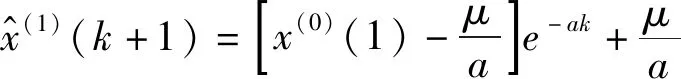
(2)

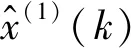
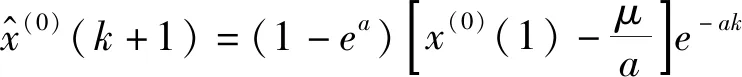
(3)

1.4 模型精度检验

求得灰色预测模型后,需要通过检验模型精度来判定模型是否满足要求。模型检验一般包括关联度检验、残差检验和后验差检验。常用残差检验和后验差检验法[5]。

(2) 计算原始序列的标准差S1和绝对误差序列的S2。

(3) 计算后验差比C=S2/S1。

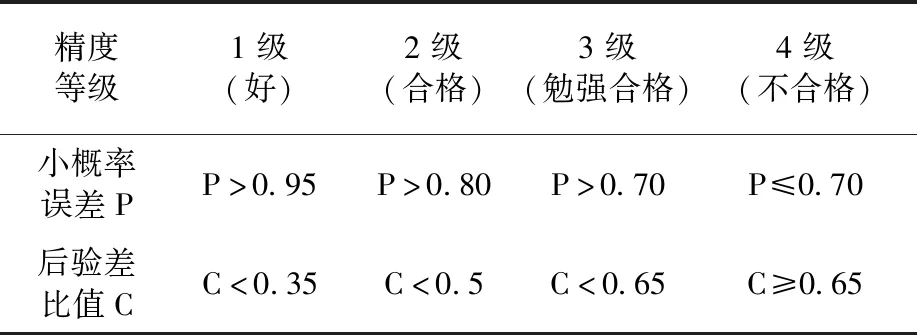
表1 精度检验等级分类对照表

1.5 等维灰数递补GM(1,1)模型建模

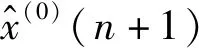
1.6 构建发展带区间模型

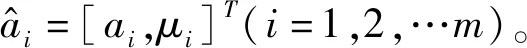
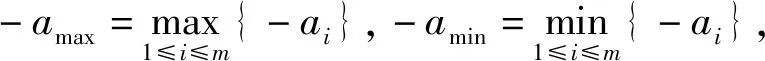
(4)

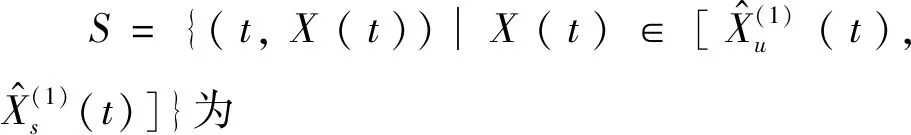
2 数据选择与建立安全生产事故GM(1,1)模型

2.1 数据来源及建模事先检验

本文选取2013-2020年我国安全生产事故相关数据进行预测,数据来源于《2014-2021中国社会统计年鉴》,见表2。对我国安全生产事故6个指标数据进行级比检验,项数为n。

取n=8,相关指标序列的级比σ∉[e-2/n+1,e2/n+1]=[0.801,1.249],不符合建模条件。

取n=7,相关指标序列的级比σ∉[e-2/n+1,e2/n+1]=[0.7788,1.284],不符合建模条件。

取n=6,只有重特大事故发生数序列的级比σ∈[e-2/n+1,e2/n+1]=[0.751,1.331],符合建模条件,其他指标的级比都不满足级比条件,不符合建模条件。

取n=5时,6个指标序列的级比σ∈[e-2/n+1,e2/n+1]=[ 0.717,1.396]且通过准光滑性检验,符合建模条件。因此,我们选择2016-2020年我国安全生产事故数序列建立GM(1,1)预测模型,预测2021-2025我国安全生产事故数据,见表2。

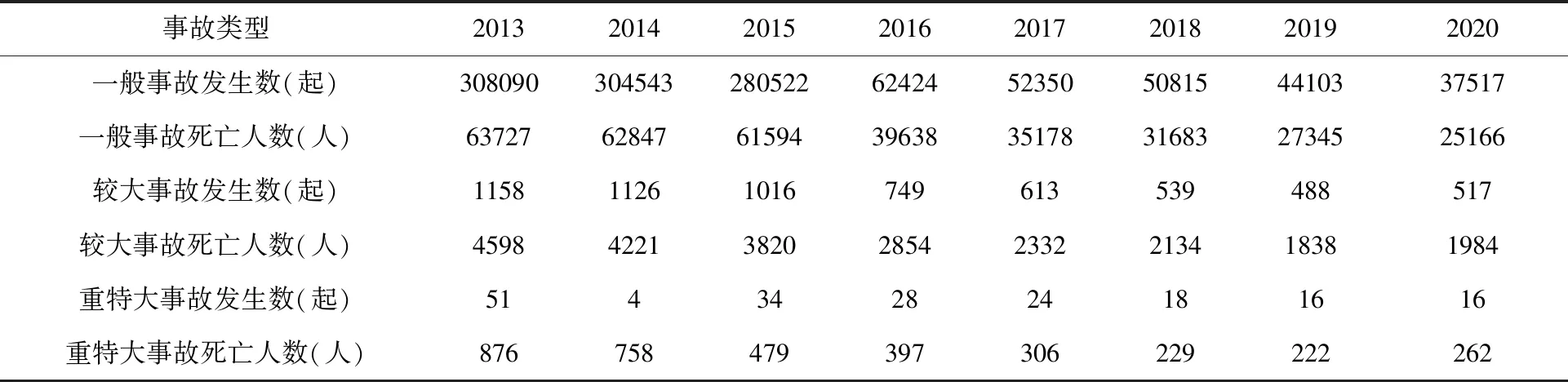
表2 2013-2020年我国安全生产事故发生数与死亡人数统计表

资料来源：《2014-2021中国社会统计年鉴》。备注：全国生产安全事故统计的项目包括：农林牧渔业、采矿业、商贸制造业、建筑业、交通运输业及其他行业。其中交通运输业包括铁路运输业、道路运输业、水上运输业和航空运输业及其他运输业。所以文章所指的安全生产数据包括与生产有关的交通事故。

2.2 构建等维灰数递补GM(1,1)模型

(1) 对原始数列构造一次累加序列

可得参数估计值为

(3) 得出预测模型：

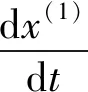
(4) 全国一般事故发生数预测模型为：

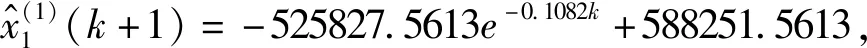
(5) 模型检验：-a=-0.1082<0.3,C=0.0441<0.35,P=1>0.95,后验差检验为1级好,根据表1,通过检验,列入表3中,可进行中长期预测分析。

(6) 等维灰数递补预测计算。依据2016-2020年我国一般事故发生数数据的GM(1,1)模型,完成对2021年预测数据,然后将2016年数据去掉,补充2021年的预测数据,再根据2017-2021年数列,重复上述步骤进行灰数递补建模完成对2022年数据的预测,直至完成对2025年的预测。同时,计算平均相对误差、后验差比C和小误差概率P值,见表4和表5。

表3 静态GM(1,1)模型及精度检验表

表4 动态GM(1,1)模拟精度检验表

2.3 对所有指标建立GM(1,1)预测模型并等维递补预测

重复上述步骤,对我国一般事故死亡人数、较大事故发生数和死亡人数、重特大事故发生数和死亡人数建立静态GM(1,1)模型并进行相关检验,列入表3中。对照表1,我国生产事故的所有数据序列的GM(1,1)模型的参数-a均小于0.3,C值均小于0.35,P值均大于0.95,均达到1级,通过检验,均能够进行中长期外推预测。进行灰数递补模拟预测平均相对误差计算和灰数递补模型的模拟精度检验,见表4。并进行等维灰数递补预测计算,见表5。

表5 我国2021-2025年生产事故数据预测表(等维灰数递补GM(1,1)模型)

2.4 安全事故数据发展带区间预测

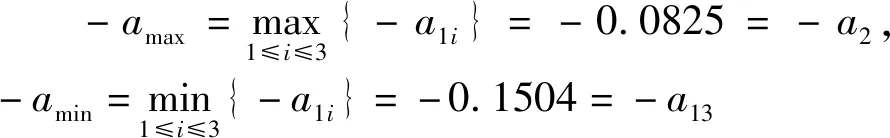
由最高值和最低值求得基本预测值,即区间的组中值。同理,求出安全事故其它数据序列的发展带上界序列响应式和下界序列响应式,见表6。进而求出2021-2025年所有安全事故数据最高值、最低值和基本预测值。最高值与最低值形成区间及其精度见表7。

表6 生产事故数据发展带上界/下界序列响应式

续表

表7 我国2021-2025年生产事故数据预测表(发展带预测值)

3 预测分析

(1) 通过等维灰数递补GM(1,1)模型分析,建立5维等维灰数递补GM(1,1)模型,提高了静态GM(1,1)模型的拟合精度和预测精度,对我国2021-2025年生产事故数据等维灰数递补预测显示：除重特大事故死亡人数呈微波动增长外,“十四五”期间预计我国一般事故、较大事故发生数和死亡人数、重特大事故发生数则呈平稳下降态势。根据模型预测,2025年我国一般事故发生数和死亡人数分别为20490起和14008人,较大事故为394起和1469人,重特大事故为8.5起和227人。

(2) 通过构建我国安全生产事故数据发展带上界与下界序列响应式区间预测,对我国2021-2025年安全生产事故数据的最低值、最高值和基本值进行预测。预测反映了我国“十四五”期间安全生产事故的发展趋势、事故数据的上下边界及中间基础值,即2025年我国一般事故发生数的预测区间和基本值为[17744,27481 ]/22613起,死亡人数为[13101,13923]/13512人;较大事故发生数为[243,451]/347起,死亡人数为[925,1568]/1247 人;重特大事故发生数为[4,12]/8起,死亡人数为[74,365]/220人,精度在94%以上。对比表5和表7,除一般事故死亡人数超出最高值外,其他事故数据等维灰数递补GM(1,1)模型的预测值保持在事故数据发展带预测最低值和最高值之间且在事故预测基本值的附近。

4 结论

(1) 预测了我国“十四五”期间安全生产事故数据与发展态势。通过等维灰数递补GM(1,1)模型和发展带区间上下界序列响应式预测模型,对我国“十四五”期间的安全生产数据进行预测,提高了静态GM(1,1)模型的拟合精度和预测精度,模型拟合精度都达到1级,区间精度达94%以上。两种模型预测一致显示：我国“十四五”期间一般事故、较大事故的发生数和死亡人数、重特大事故发生数的数据均呈不同程度的下降,而重特大事故死亡人数则呈波动微升态势。因此,发展带区间模型预测的事故数据最高值和最低值,可作为我国2021-2025年安全管理工作中事故预防的上界警戒值和下界最优值,而发展带预测事故数基本值和等维灰数递补GM(1,1)模型预测值可作为我国同期安全生产事故数的目标参考目标值和评价值。

(2) 提出我国安全生产行为或运行系统已经发生了系统性变化。自2015年之后(包含之前的安全工作扰动因素的持续作用),我国在安全生产方面的发展与改革(扰动因素)基本是成功的,已经改变我国安全生产行为运行的特性,导致我国安全生产事故相关数据整体呈逐年下降趋势。但是模型预测显示,未来几年我国重特大事故死亡人数依然高居不下,且有回升趋势。因此,在化解和防止重特大事故死亡人数方面,安全扰动因素作用依然存在不足,需要强化实施针对重特大事故死亡人数的安全政策体系与措施方案。

(3) 依据我国安全生产事故新一年的数据置入到原数据中,运用新信息GM(1,1)预测,进一步提高最近一、两年事故数据的预测精度。研究表明要从根本上提高我国安全生产管理水平和扭转安全生产事故,就必须对生产过程继续强化安全扰动因素,全方位改善和提升我国的安全生产行为运行系统。事故预测为政府相关部门制定安全生产规则、安全投资政策、安全生产发展规划及开展安全行动方案提供基础支撑数据。