桥上CRTSⅢ型无砟轨道断缝值计算模型研究

桂昊、连西妮、梁斌

（柳州铁道职业技术学院，广西 柳州 545616）

0 引言

我国自主研发的CRTSⅢ型板式无砟轨道广泛应用在高速铁路桥上无缝线路[1]，在冬季低温环境下，桥上无缝线路在伸缩力峰值[2]或焊缝位置存在断轨风险[3]，危及桥上行车安全。因此，断缝值和断轨力检算是桥上无缝线路设计的控制性因素[4]。

现有关桥上无缝线路断缝值和断轨力方面的研究，大多采用公式法和简化的平面或空间力学模型。龚小平[5]提出一种解析法计算桥上无缝线路断轨力；魏贤奎等[6]建立了线-桥-墩平面力学模型，指出上承式拱桥无缝线路断缝值的简化算法计算结果与实际情况有较大差别；郑鹏飞等[7]针对斜拉桥上无缝线路，基于所建立的平面力学模型对断缝值影响因素进行了分析。桥上无缝线路长钢轨在低温条件下发生断轨时往往是单股钢轨折断，并在梁-板-轨的相互作用下形成新的力学平衡体系，现有的公式法和简化的平面力学模型无法体现出轨道、桥梁等结构的空间受力特点及其相互作用关系。

本文基于墩-梁-板-轨相互作用机理和有限元法，建立桥上CRTSⅢ型无砟轨道无缝线路精细化有限元模型，对钢轨断缝值、断轨力进行计算分析。

1 精细化有限元模型

1.1 模型组成部分

基于图1 所示的桥上CRTSⅢ型板式无砟轨道无缝线路墩-梁-板-轨相互作用机理，以5×32m 简支梁+（70+130+70）m 连续梁+5×32m 简支梁桥为例，建立详细考虑各细部结构的桥上CRTSⅢ型板式无砟轨道无缝线路精细化有限元模型，如图2 所示。其中，CHN60 钢轨采用铁摩辛柯梁单元模拟；轨道板、自密实混凝土层、凸台、弹性垫层、底座板、简支箱梁和连续箱梁均采用实体单元模拟；固定支座桥墩/台顶纵向刚度采用线性弹簧单元模拟；采用非线性弹簧单元模拟WJ-8 型扣件阻力r，并按式（1）计算取值。

图1 桥上CRTSⅢ型板式无砟轨道无缝线路墩-梁-板-轨相互作用机理

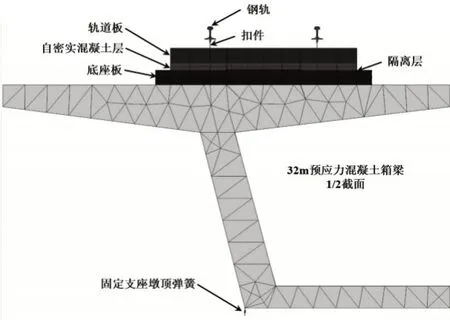
图2 精细化有限元模型横断面

1.2 断缝值与断轨力理论计算公式

钢轨断缝值和作用在墩台上的断轨力理论计算公式如式（2）和式（3）所示[8]。

式（2）中：λ为钢轨断缝；E为钢轨弹性模量；F为钢轨横断面面积；α为钢轨钢线膨胀系数；ΔTdmax为最大降温幅度；r为线路纵向阻力为钢轨断缝容许值；L为一跨（联）梁梁长。

1.3 温度荷载及计算假定

1.3.1 采用降温荷载，钢轨降温60℃，轨道板竖向考虑大小为45℃/m 的负温度梯度[9]，其余考虑整体降温20℃。

1.3.2 在附加伸缩力的影响下，连续梁桥上无缝线路温度力在最大温跨活动支座墩顶处达到最大，故假定在该处发生断轨。

1.4 主要物理量及其符号表示

本文模型所提取的数据中，主要结构物理量及其符号表示如表1 所示。

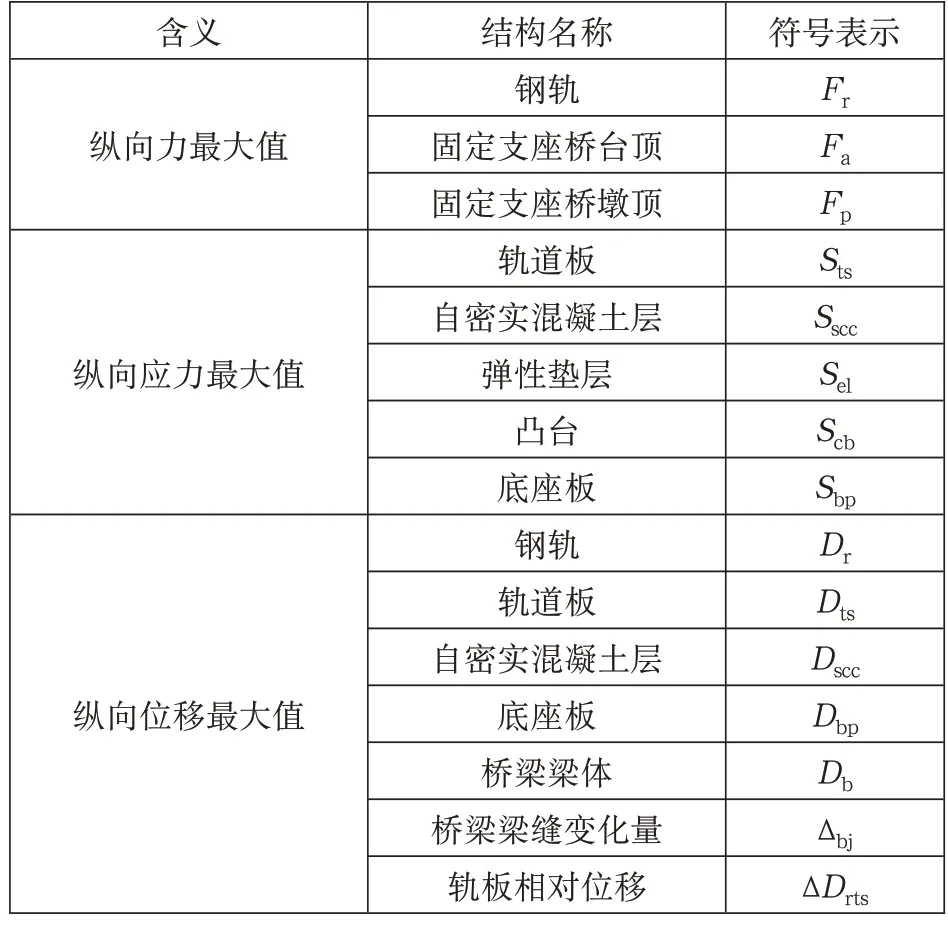
表1 主要结构物理量及其符号表示

2 模型验证

本文选取同为单元板式结构的桥上CRTSⅠ型板式无砟轨道进行对比，建立与已有文献相同桥跨模型[10]。在相同工况下，两种模型计算出的钢轨纵向力分布规律及其峰值大小基本一致，钢轨纵向力最大值误差仅为2%，表明本文建模方法的正确性和计算结果的可靠性。

3 桥上无缝线路断缝值计算

本节考虑在降温荷载作用下，主桥右侧活动支座桥墩顶处一股钢轨发生折断（1 号钢轨折断、2/3/4 号钢轨状态良好）和未断轨（1/2/3/4 号钢轨状态均良好）两种计算工况。钢轨和桥墩/台顶纵向力见图3，钢轨纵向位移和轨板相对位移见图4，各结构纵向力与位移最大值计算结果见表2。

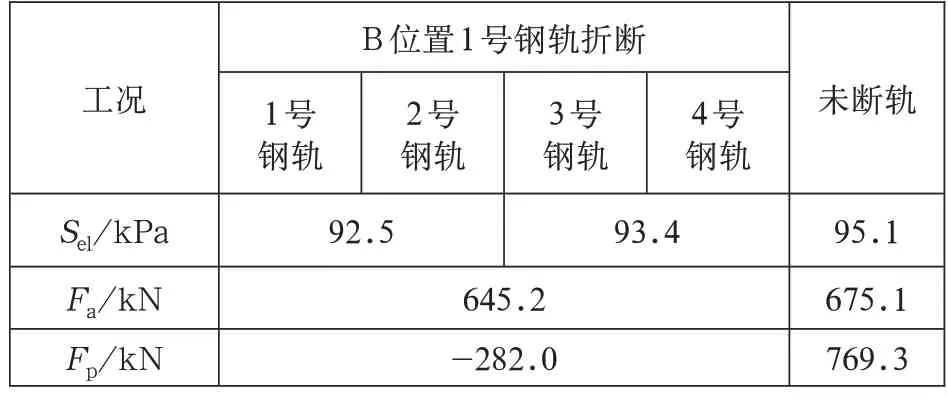
表2 （续）

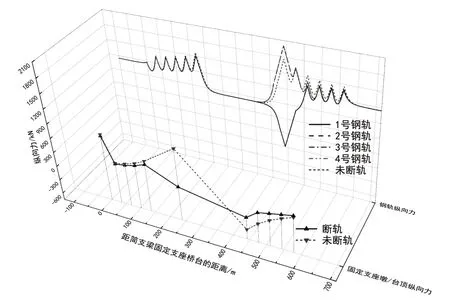
图3 钢轨和桥墩/台顶纵向力

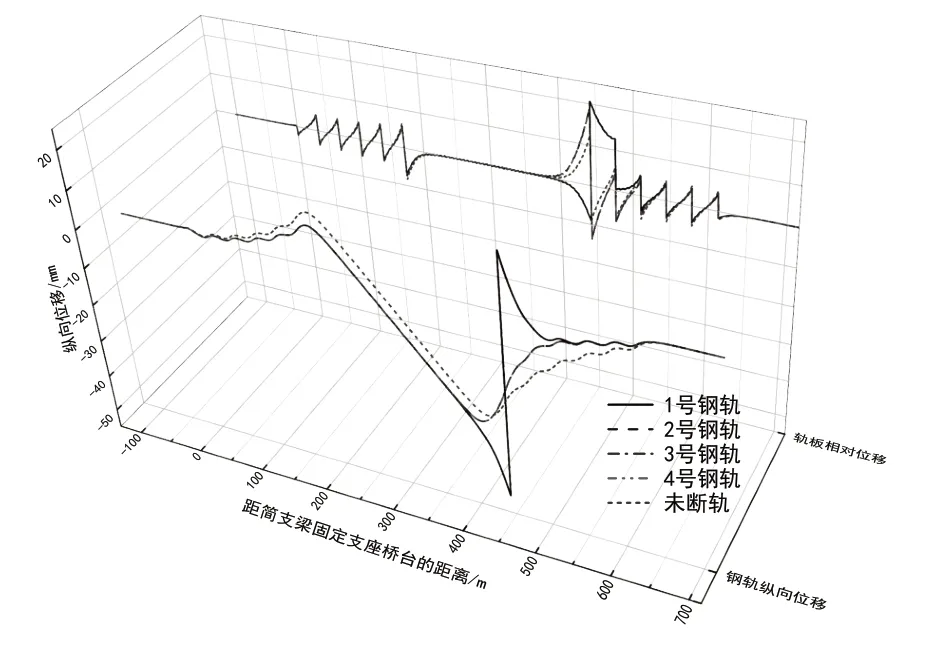
图4 钢轨纵向位移和轨板相对位移

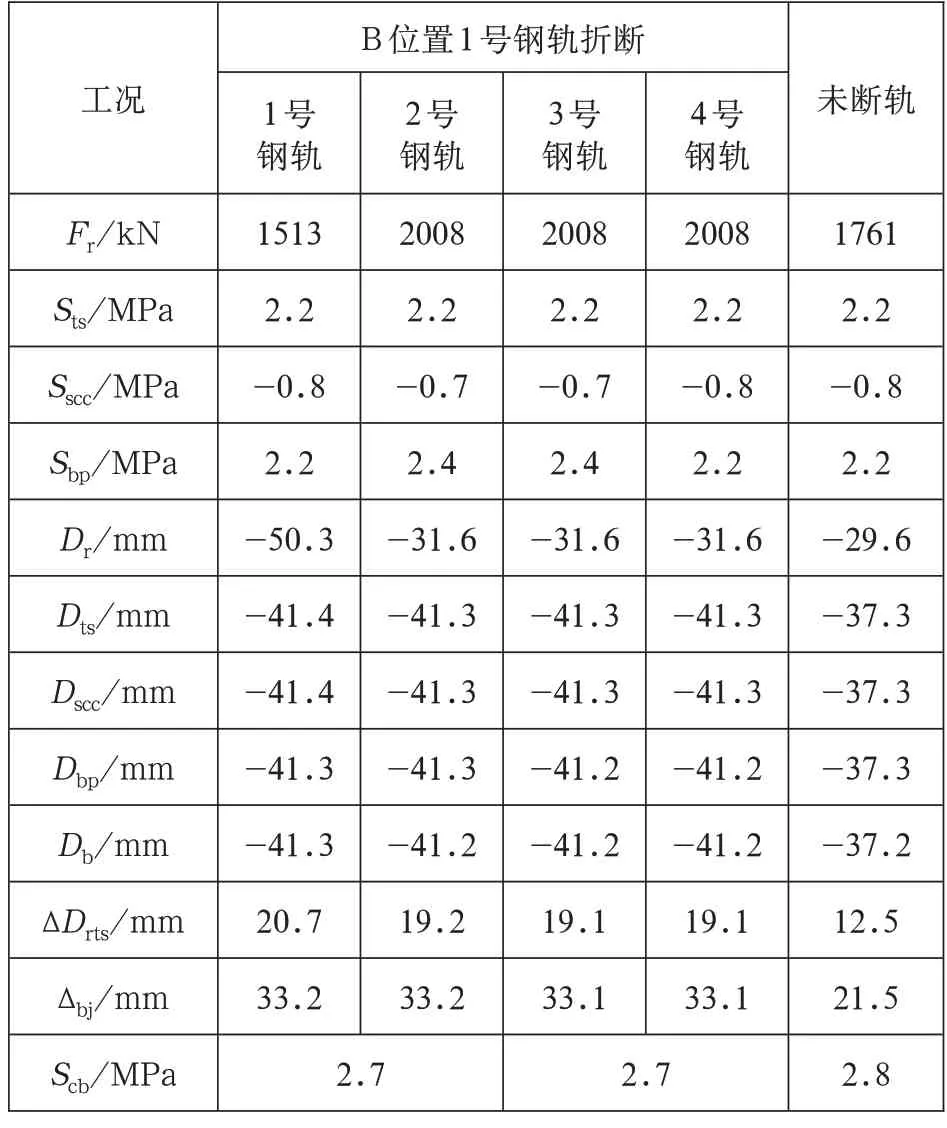
表2 各结构纵向力与位移最大值

由图3、图4 和表2 可知：极端低温条件下，无缝线路长钢轨在温度拉力作用下发生断轨并收缩形成断缝，断缝值达到63.1mm；折断钢轨（1 号钢轨）纵向力在断缝位置急剧降低至零，由于双线轨道和桥梁结构的整体性，折断钢轨的收缩对同线和邻线非折断钢轨（2 号和3 号、4 号钢轨）均产生了一定的附加拉力增量，从而增加了非折断钢轨出现断轨的风险；无砟轨道层纵向应力变化很小，桥梁和轨道结构纵向位移变化较大；轨板相对位移在断缝处突增至最大值后急剧降低至反向最大值、达到20.7mm，大大增加了断缝处扣件橡胶垫板滑出的风险。

相比未断轨，发生断轨后的折断钢轨纵向拉力最大值减小了14%，钢轨纵向位移最大值增大了70%，轨板相对位移和梁缝增量最大值分别增大了65% 和54%；同线非折断钢轨和邻线非折断钢轨的纵向力、位移峰值大小基本一致，其中，钢轨纵向拉力最大值均增大了14%，钢轨纵向位移最大值均增大了7%，轨板相对位移和梁缝增量最大值分别增大了53%和54%；而固定支座墩顶纵向力发生明显变化，距离断缝较近的6号墩和8 号墩顶纵向力变化量分别达到了795.1kN 和262.0kN，即作用在6 号墩顶的断轨力为795.1kN。

根据式（1）和式（2），采用公式法计算钢轨在降温60℃条件下发生断轨时的断缝值λ=33.3mm，仅为本文模型计算结果的0.53 倍，这是由于公式法计算断缝值时并未考虑到桥上无缝线路伸缩附加力对断缝扩展的影响。根据式（1）和式（3），采用公式法计算作用在墩台上的断轨力T3=1128.5kN，为本文模型计算结果的1.4 倍，这是由于公式法计算断轨力时未考虑双线轨道和桥梁结构的整体性，发生断轨后，同线及邻线非折断钢轨、相邻桥墩均会承担部分断轨力。本文所建立的精细化有限元模型则详尽考虑了以上因素，其计算的断缝值和断轨力更能反映出桥上无缝线路的实际状态。

4 结论

通过建立桥上CRTSⅢ型无砟轨道精细化有限元模型，计算并分析桥上无缝线路断缝值和断轨力，得出如下结论：

其一，双线桥上无缝线路一股钢轨发生断轨，折断钢轨的纵向力、纵向位移和轨板相对位移均在断缝处发生突变，且使同线和邻线非折断钢轨均产生14%的附加拉力，需重点对断缝位置的断缝值、轨板相对位移及断轨力进行检算。

其二，轨温降低60℃、主桥右侧活动支座墩顶处断轨的工况下，本文模型计算的断缝值和断轨力分别达到了63.1mm 和795.1kN，分别为公式法计算结果的1.9 倍和0.7 倍。

其三，公式法计算的断缝值偏小、断轨力偏大，存在一定的局限性；相较于公式法和简化的平面力学模型，本文所建立的精细化有限元模型能够反映出断轨工况下桥墩、箱形梁和无砟轨道各细部结构的空间力学特性实质，计算结果更加精确。