浅埋煤层快速掘进巷帮蠕变效应及滞后支护
2023-05-17黄庆享杜君武毛小娃杨涵问
黄庆享,赵 灿,杜君武,高 彬,毛小娃,杨涵问
(1.西安科技大学 能源学院,陕西 西安 710054;2.西安科技大学 西部矿井开采及灾害防治教育部重点实验室,陕西 西安 710054;3.陕煤集团神木张家峁矿业有限公司,陕西 神木 719300)
0 引 言
近年来,随着采煤装备水平的提高,回采速度加快,采掘接续日趋紧张。提高巷道掘进效率,缓解采掘接续紧张局面,成为矿井高效开采亟待解决的问题[1]。根据《煤矿巷道锚杆支护技术规范》[2]规定:掘进工作面严禁空顶作业;若两帮围岩稳定,帮锚杆施工可适当滞后。实践表明,不同矿井巷道围岩条件各异,巷道掘进采用的两帮滞后支护时间和距离差异较大。两帮滞后支护时间(距离)过小,支护与掘进工序相互影响,制约巷道掘进效率;两帮滞后支护时间(距离)过大,影响巷道支护效果和安全。因此,确定合理的两帮滞后支护距离和时间,对巷道安全和快速掘进具有重要意义。
国内外学者对巷道围岩变形时空效应和稳定性方面展开了大量研究。董方庭、宋宏伟等建立了巷道围岩松动圈支护理论,提出基于松动圈的围岩分类方法和锚喷支护机理[3-4]。黄庆享等根据巷道围岩自稳平衡现象,建立了巷道极限自稳平衡圈理论,提出“治顶先治帮,治帮先治底”的巷道支护理念[5]。李晓斌等进一步研究巷道围岩稳定性分类方法[6-9]。范庆忠分析巷道围岩蠕变衍生机制,提出强度极限临域内的岩石蠕变扰动效应理论[10]。刘朝科等对围岩进行蠕变试验,得到三轴压缩下围岩蠕变变形规律和破坏特征[11-12]。王芝银等基于岩石流变理论,研究不同应力状态下岩石黏弹塑性变形全过程的蠕变方程、蠕变破坏时间、蠕变变形与破坏属性[13]。陈卫忠、屈丽娜等通过三轴流变试验分析煤巷围岩蠕变规律,为预测巷道长期变形和确定合理支护方式提供依据[14-15]。马睿研究煤巷快速掘进顶板稳定性,提出合理的滞后支护方案[16]。综上所述,当前对巷道围岩滞后支护主要采用物理试验、数值模拟、理论分析等研究方法,都强调巷道围岩蠕变对巷道稳定性的影响,重点关注滞后支护距离对巷道稳定性的影响,对滞后时间的研究相对较少。
由于榆神府矿区浅埋煤层地压较小[17],煤层较稳定,煤巷掘进中通常根据经验采用两帮滞后支护以提高掘进速度。目前,对两帮滞后支护时间研究较少,实践中根据经验确定滞后支护时间存在一定的盲目性和安全隐患。以榆神府矿区张家峁煤矿14213胶带运输巷为研究对象,采用现场调查、理论分析和FLAC3D数值计算相结合的方法,研究煤巷掘进围岩蠕变规律与稳定性,确定两帮合理滞后支护时间,为煤巷安全快速掘进提供理论依据。
1 工程背景
1.1 掘进巷道地质概况
张家峁煤矿14213胶带运输巷(简称运输巷)位于4-2煤层,平均厚度3.34 m,平均埋深151.2 m,煤层倾角0.3°左右。覆岩土层厚度一般40 m左右,基岩厚度111.2 m。煤层直接顶为砂质泥岩,厚2.42 m,泥质胶结,饱和抗压强度17.16×106Pa,属不稳定型顶板。基本顶为细粒砂岩,交错层理发育,孔隙式泥质胶结,厚17.76 m,饱和抗压强度28.36×106Pa,属较稳定型顶板。直接底为泥质粉砂岩,厚1.37 m,饱和抗压强度为11.65×106Pa,属较软底板。运输巷煤层顶底板钻孔柱状如图1所示。
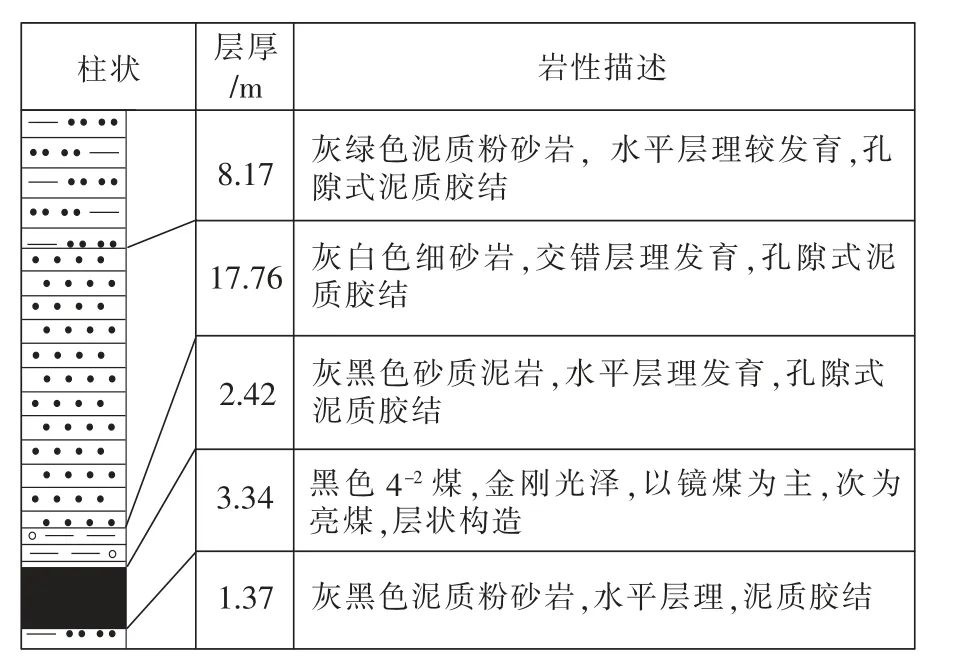
图1 运输巷钻孔柱状图Fig.1 Column diagram of borehole in headgate
1.2 巷道断面形状及支护参数
运输巷断面形状为矩形,巷道宽6.0 m,高3.3 m,断面面积19.8 m2。顶板采用锚网支护,帮部采用锚杆支护,巷道断面如图2所示。
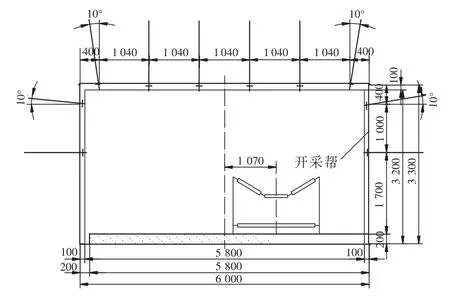
图2 巷道支护断面(mm)Fig.2 Section of headgate support
顶板锚杆间距1 040 mm,排距1 200 mm,顶部最外侧锚杆距帮400 mm,向帮部偏斜10°布置,其余锚杆垂直布置,每排6根锚杆,锚杆初始锚固力大于60 kN,预紧扭矩大于100 N·m。帮部锚杆间距1 000 mm,排距1 200 mm,帮部最上方锚杆距顶板500 mm,向顶部偏斜10°布置,其余锚杆均垂直轮廓线布置,每排4根锚杆。非开采帮锚杆采用φ22 mm×1 800 mm左旋螺纹钢锚杆,锚杆初始锚固力不低于60 kN,预紧扭矩不低于100 N·m。开采帮采用φ20 mm×1 800 mm玻璃钢锚杆,锚杆初始锚固力不低于60 kN,预紧扭矩不低于60 N·m。
2 巷道两帮稳定性和失稳范围分析
2.1 巷道围岩松动圈分析
巷道开挖后,围岩应力重新分布,当应力达到或超过围岩强度时围岩发生破坏,从巷道周边逐步向深部扩展形成围岩松动圈[18-19],如图3所示。
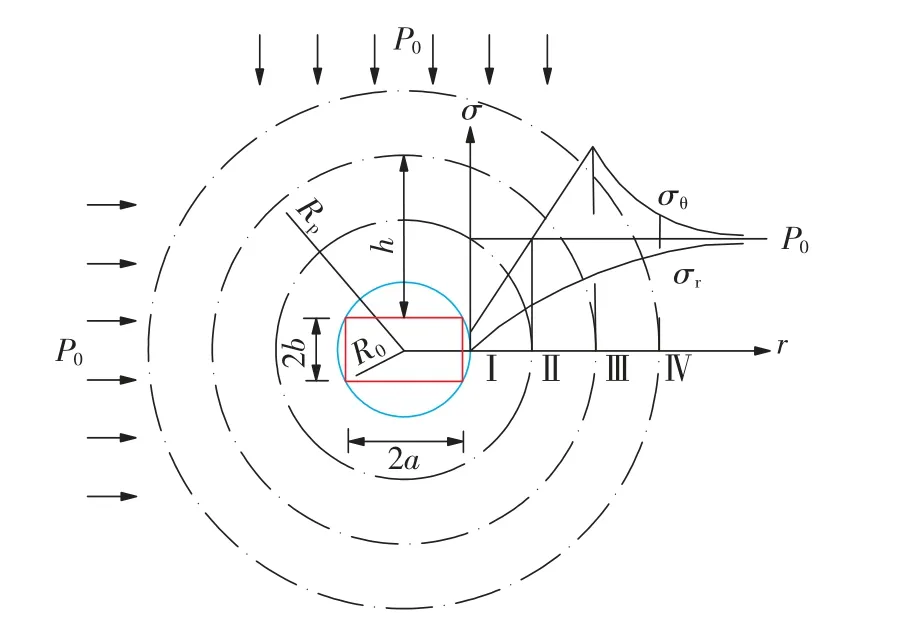
图3 巷道开挖后围岩应力分布状态Fig.3 Stress distribution of surrounding rock after headgate excavation
巷道围岩松动圈的大小、围岩强度和应力相关,巷道支护的作用主要是增强松动区(Ⅰ区)围岩残余强度,抑制碎胀变形,控制裂隙发育。对于矩形巷道,确定巷道松动圈的方法主要有等效圆法[20-21],将矩形巷道等效为圆形巷道,通过计算圆形巷道塑性区范围确定其松动范围。
根据莫尔-库伦强度准则及弹性理论可知,静水压力作用下的圆形巷道在弹性区和塑性区的径向应力和切向应力为
式中 σer为弹性区径向应力,Pa;σeθ为弹性区环向应力,Pa;σpθ为塑性区径向应力,Pa;σpr为塑性区环向应力,Pa;r为围岩中任一点与等效圆形巷道中心的距离,m;p0为原岩应力,Pa;Rp为塑性区半径,m;R0为圆形巷道半径,m;C为围岩的黏聚力,Pa;φ为围岩的内摩擦角,(°)。
根据图3,切向应力σθ的最大值位于巷道弹、塑性区的交界处,由交界处向巷道周边逐渐减小并恢复至原岩应力状态。由于巷道的弹、塑性边界处σθ相等,由式(2)和式(4)得,松动圈半径为
设矩形巷道宽度为2a,高度为2b,则矩形巷道的等效圆形巷道半径,代入式(5)则可以得出等效松动圈半径。则矩形巷道顶板松动高度hct和两帮松动宽度hcs分别为
式中 a为矩形巷道宽度的一半,m;b为矩形巷道高度的一半,m。
2.2 巷道围岩松动范围及稳定性类型确定
根据运输巷围岩和覆岩资料,基岩平均容重为24 kN/m3,土层平均容重为18 kN/m3;4-2煤层内摩擦角平均为37.41°,黏聚力为1.46×106Pa。巷道宽度6.0 m,高度3.3 m,即a=3.0 m,b=1.65 m,等效圆形巷道半径R0=3.42 m。将相关参数代入式(5)、式(6)和式(7),可得运输巷顶板松动范围hct=1.87 m,两帮松动范围hcs=0.52 m。
根据围岩稳定性分类[3],见表1,运输巷两帮松动圈位于40~100 cm,属于较稳定围岩。因此,该运输巷围岩较稳定,具备滞后支护条件。
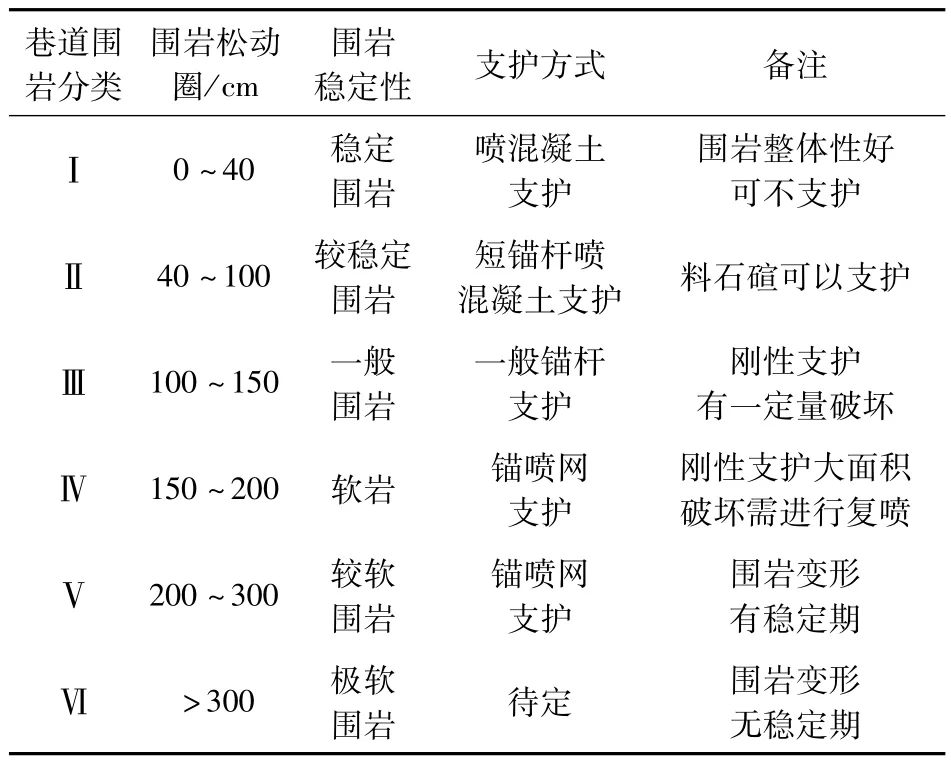
表1 围岩稳定性分类Table 1 Classification of surrounding rock stability
3 巷道围岩蠕变时间效应
巷道围岩的蠕变[22]一般包含初始蠕变Ⅰ、稳定蠕变Ⅱ和加速蠕变Ⅲ的3个阶段,如图4所示。围岩蠕变主要是由岩石损伤随时间演化引起的,岩石损伤具有一定的临界值,当应力水平低于岩石损伤临界值,岩石将发生稳定蠕变,不会发生破坏;当应力水平达到岩石损伤临界值时,岩石微裂隙将加速扩展,出现加速蠕变,最终岩石发生破坏。因此,巷道滞后支护必须在加速蠕变阶段前进行,将巷道围岩变形控制在稳定蠕变阶段,保障巷道安全。
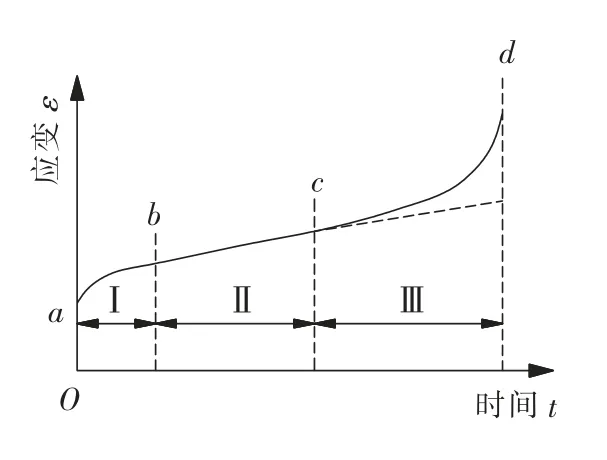
图4 岩石蠕变过程Fig.4 Creep process of rock
Cvisc流变模型是将马克斯韦尔(Maxwell)模型、开尔文(Kelvin)模型和塑性元件(St.V体)串联,即柏格斯(Burgers)模型与一个塑性元件串联得到的黏弹塑性模型,如图5所示。图中σ为岩体应力,EM,EK,ηM,ηK分别为马克斯韦尔弹性模量、开尔文弹性模量、马克斯韦尔黏性系数和开尔文黏性系数;σf为屈服应力,若外力小于σf,则不会产生变形,一旦当σ达到σf时,会在等应力下出现塑性流变;εM,εK,ερ分别为马克斯韦尔体、开尔文体的应变和塑性应变。Cvisc流变模型可呈现岩土弹性、塑性和粘性特性,能够描述压缩及剪切流变特性[23],能够准确反映巷道围岩蠕变特性。
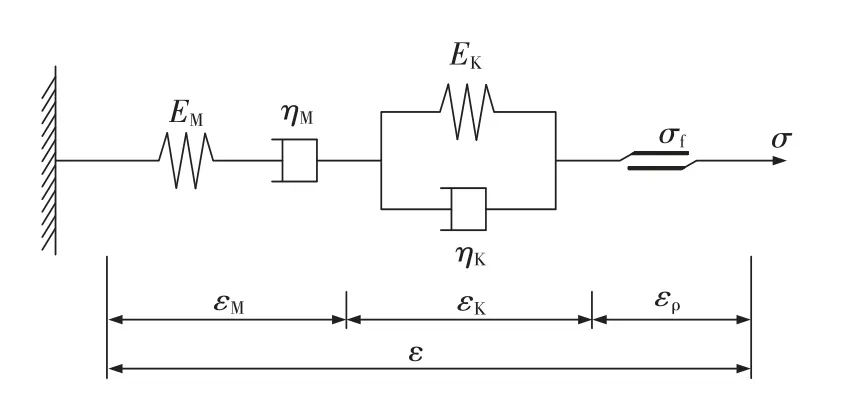
图5 Cvisc流变模型Fig.5 Cvisc rheological model
如图5所示,Cvisc流变模型由理想弹簧、理想黏壶和塑性元件3种基本元件组成,可得
由式(8)、式(9)得出柏格斯(Burgers)模型一维蠕变方程为
因此,Cvisc模型一维蠕变方程为
采用Cvisc流变模型,模型参数赋值时除了考虑煤岩力学参数外,还考虑开尔文黏性系数ηK,马克斯韦尔黏性系数ηM,膨胀角α,开尔文剪切模量GK和马克斯韦尔剪切模量GM,可通过剪切模量与弹性模量的换算关系由开尔文剪切模量和马克斯韦尔剪切模量换算出对应的弹性模量,煤岩力学参数可反演出蠕变参数。基于Cvisc模型的FLAC3D软件完成式(8)~式(11)的运算,可以模拟巷道围岩蠕变过程和规律,结果更加接近实际。
4 巷道蠕变模拟及两帮滞后支护时间确定
为揭示巷道开挖后两帮变形与破坏时间效应,采用FLAC3D中的Cvisc蠕变模型模拟14213胶带运输巷两帮不同滞后支护时间下的变形破坏规律,确定合理的两帮滞后支护时间。
根据4-2煤层地质条件及巷道煤岩力学参数构建FLAC3D数值计算巷道模型,煤岩力学参数见表2,模型走向长度86 m,倾向长度100 m,高度54.5 m,模拟巷道断面宽6 m,高3.3 m。模型共计172 200个单元,182 019个节点。模型顶部为自由边界,底部为固定边界,模型前后左右限制水平位移,由于模型未模拟至地表,模型以上部分根据岩层厚度及容重计算得出顶部施加2.1 MPa的等效载荷。
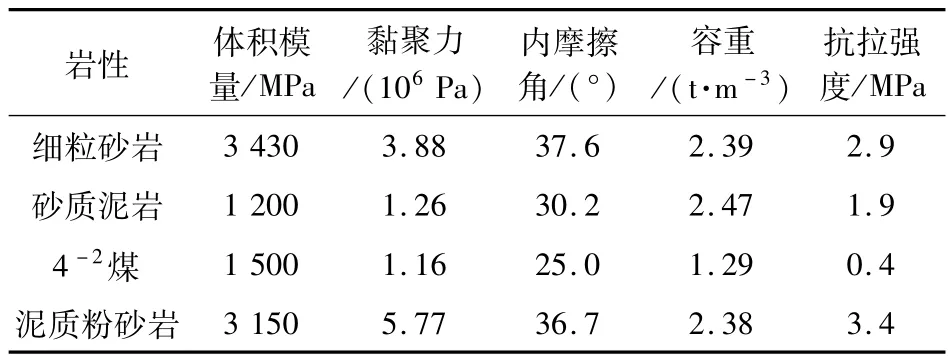
表2 煤岩力学参数Table 2 Mechanical parameters of coal and rock
巷道顶板锚杆支护对于巷道围岩稳定具有重要作用。为了分析巷道顶板支护强度对两帮蠕变效应的影响,采用FLAC3D模拟不同顶板支护强度下的巷道两帮变形情况,如图6所示。可见,2~38 d内,顶板不支护、顶板锚杆支护60 kN锚固力和120 kN锚固力3种情况的两帮移近量接近;40 d后,顶板不支护相较于顶板锚杆支护时两帮移近量有所增加,最大达到295 mm;顶板锚杆支护120 kN锚固力相较于60 kN锚固力的两帮移近量略有减小,2种情况两帮变形量接近。考虑到60 kN锚固力施工难度较120 kN锚固力小,确定合理的顶板锚杆锚固力为60 kN。
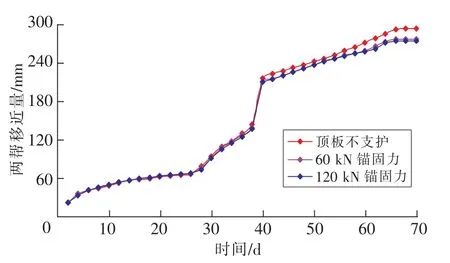
图6 不同顶板支护情况下两帮蠕变Fig.6 Creep of two ribs under different roof support
4.1 仅顶板支护时围岩蠕变规律与时间效应
运输巷开挖后,对顶板进行及时的锚杆支护,两帮不支护,数值计算模型如图7所示。运输巷开挖后仅顶板支护时,水平位移分布如图8所示,巷道两帮移近量蠕变曲线如图9所示。
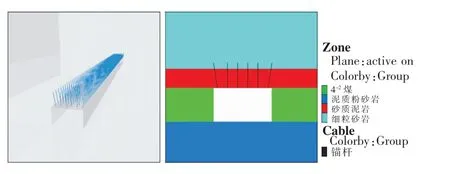
图7 巷道仅顶板支护时计算模型Fig.7 Calculation model of headgate with only roof support
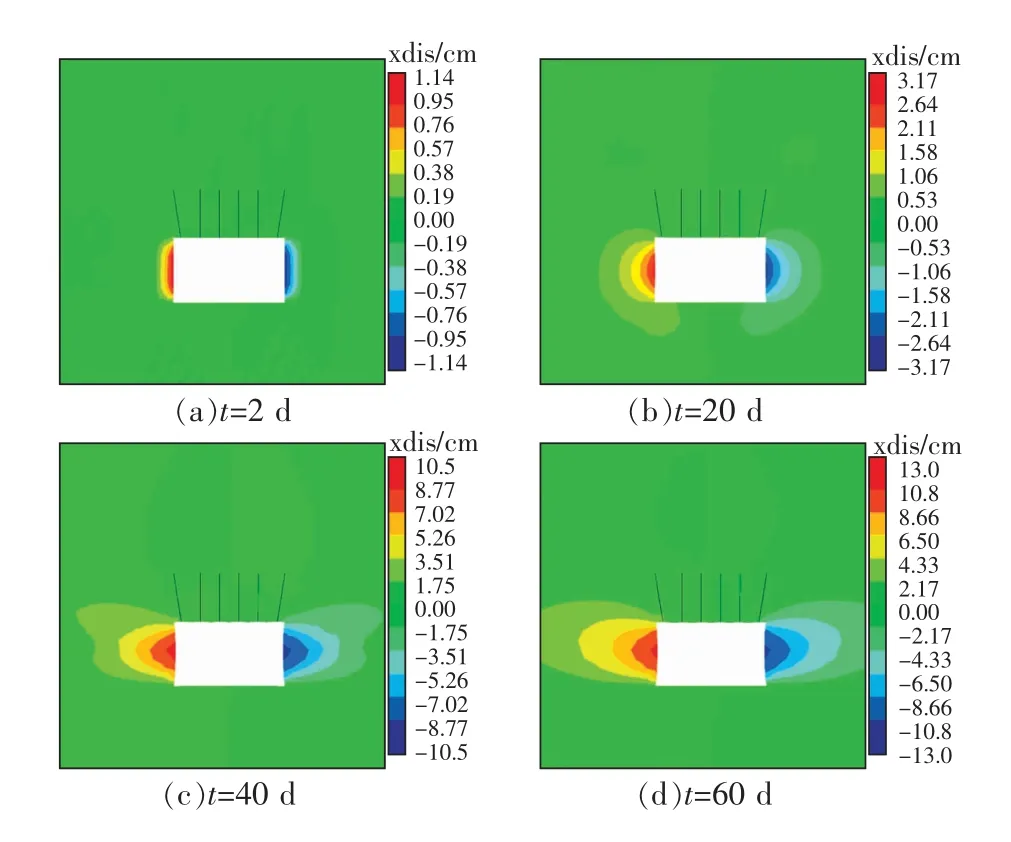
图8 巷道仅顶板支护时水平位移分布Fig.8 Horizontal displacement distribution of headgate with only roof support
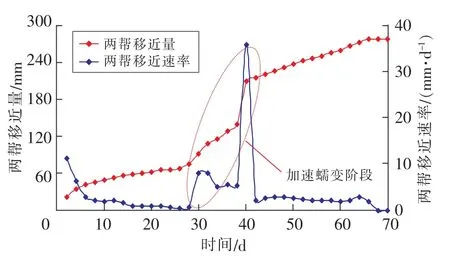
图9 巷道仅顶板支护时两帮移近蠕变Fig.9 Approaching creep of two ribs of headgate with only roof support
4.1.1 巷道两帮移动变形时间效应
1)初始蠕变阶段。巷道开挖5 d内,两帮移近速率由10 mm/d迅速下降,并稳定3 mm/d以内。
2)稳定蠕变阶段。巷道开挖6~28 d内,两帮移近速率由3 mm/d缓慢下降为1 mm/d,以平均2 mm/d稳速移近,移近量增长缓慢。
3)加速蠕变阶段。巷道开挖29 d后,进入加速蠕变阶段。巷道开挖29~40 d,两帮移近变形出现加速蠕变,40 d时,两帮移近速率增加至36 mm/d,增大了18倍,巷道两帮变形剧烈,承载能力和稳定性明显下降。巷道开挖40 d后,两帮移近速率下降至3 mm/d内。65 d后两帮移近量稳定在278 mm。
4.1.2 巷道两帮塑性区发育时间效应
仅顶板支护情况下,运输巷两帮塑性区随时间变化规律如图10所示。巷道开挖28 d以内,两帮塑性区深度为0.5 m,范围较小。巷道开挖40 d以后,两帮塑性区发育深度达到1.3 m,并且随着时间的增长,塑性区范围不断扩大。
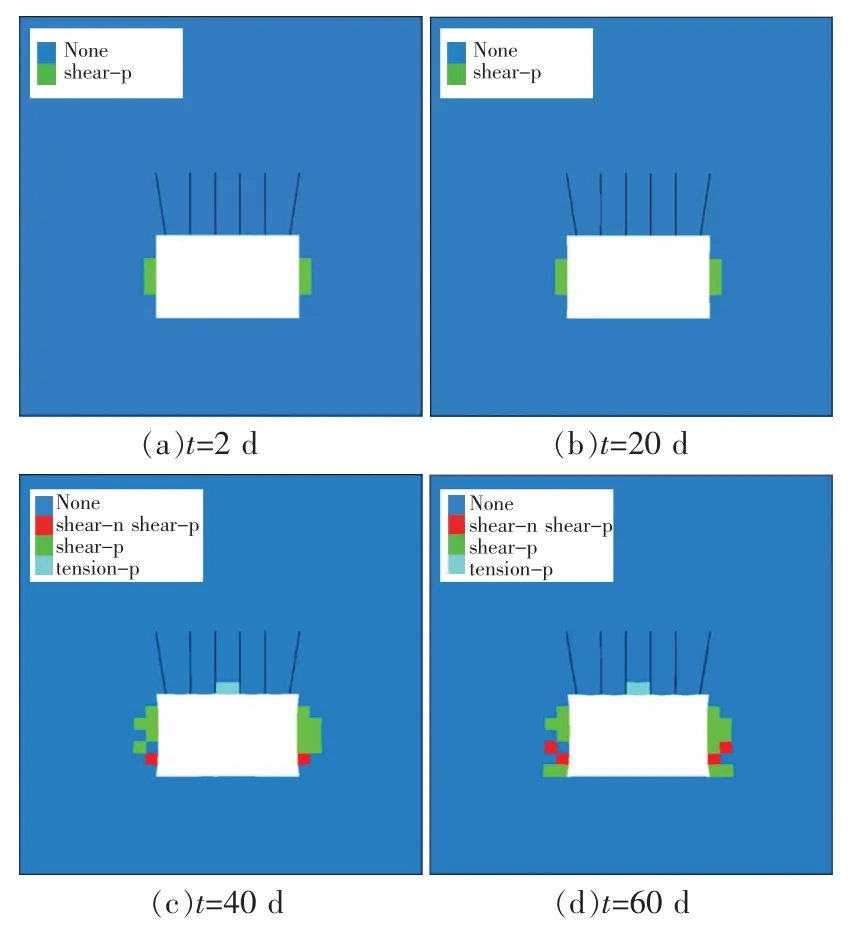
图10 巷道仅顶板支护时塑性区分布Fig.10 Plastic zone of headgate with only roof support
4.1.3 巷道顶板下沉时间效应
仅顶板支护情况下,运输巷顶板下沉蠕变如图11所示。巷道刚开挖顶板下沉速率3.8 mm/d,然后迅速下降。开挖4~29 d顶板下沉速率稳定在0.25~0.8 mm/d,基本处于稳速变形。巷道开挖30~31 d时,顶板下沉速率上升至3.3~3.5 mm/d,然后迅速下降并稳定在0.3 mm/d以内。开挖40 d后顶板下沉稳定,最大下沉量35.3 mm。巷道顶板下沉未出现加速蠕变,表明顶板及时支护效果明显。
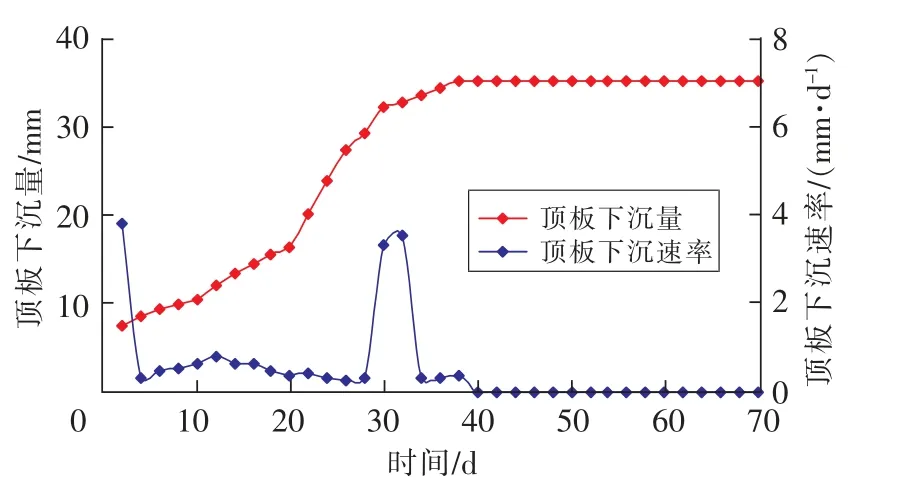
图11 巷道仅顶板支护时顶板下沉蠕变Fig.11 Roof subsidence creep of headgate with only roof support
综上分析,巷道开挖28 d内两帮处于稳定蠕变期,29 d后开始加速蠕变,两帮滞后支护需在巷道掘进28 d内进行。
4.2 两帮滞后支护时围岩蠕变规律与时间效应
为保证巷道稳定性,必须在两帮加速蠕变之前进行滞后支护。为此,开展了巷道两帮滞后支护的模拟,滞后支护选择在巷道开挖后28 d进行(巷道加速蠕变前),如图12所示。
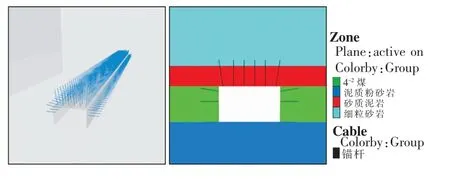
图12 巷道两帮滞后支护计算模型Fig.12 Calculation model of headgate with two ribs lag support
4.2.1 巷道两帮移动变形时间效应
运输巷两帮滞后支护后,水平位移如图13所示,两帮移近蠕变曲线如图14所示。
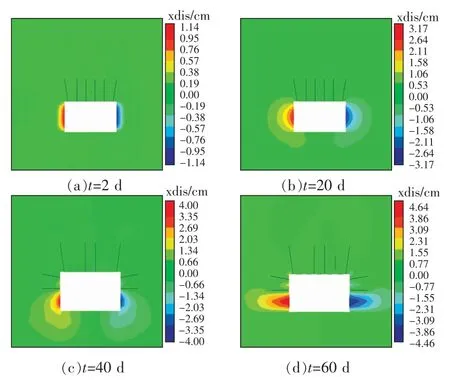
图13 巷道两帮滞后支护时水平位移分布Fig.13 Horizontal displacement distribution of headgate with two ribs lag support
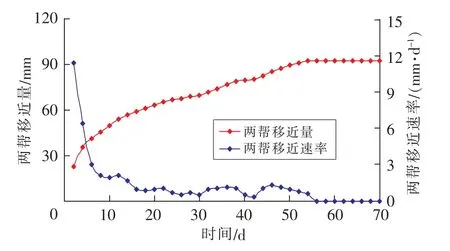
图14 巷道两帮滞后支护时两帮移近蠕变Fig.14 Approaching creep of two ribs of headgate with two ribs lag support
巷道掘进滞后28 d进行两帮支护后,巷道两帮移近速率由支护前的平均2 mm/d降为0.9 mm/d,下降了55%。巷道两帮移近变形在56 d后达到稳定,未出现加速蠕变,两帮最大移近量为92.8 mm,比两帮不支护减小67%。巷道顶板和两帮稳定,说明在加速蠕变前进行滞后支护效果明显。
4.2.2 巷道两帮塑性区发育时间效应
巷道两帮滞后支护时,随着时间的增加,巷道顶板未出现拉破坏,仅在巷帮及顶板中部出现小范围塑性区,如图15所示。巷道开挖40 d后,两帮的塑性区发育深度0.5 m,比两帮不支护减小61.5%。
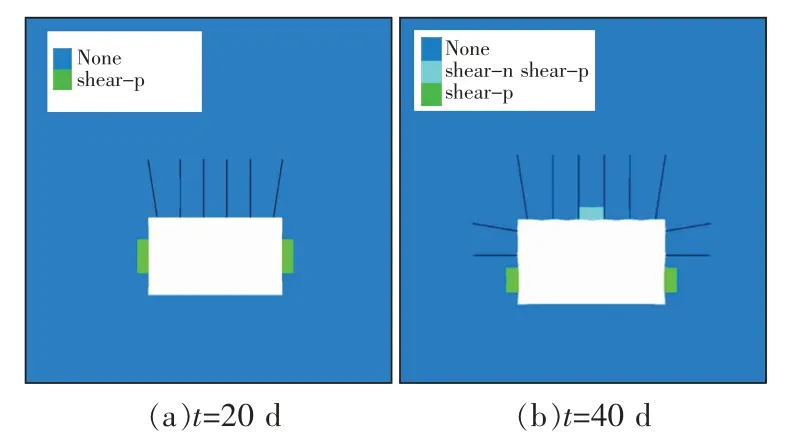
图15 巷道两帮滞后支护时塑性区分布Fig.15 Plastic zone of headgate with two ribs lag support
4.2.3 巷道顶板下沉时间效应
巷道两帮滞后支护情况下,巷道顶板下沉蠕变曲线如图16所示。开挖20~40 d顶板下沉速率在0.5~2.2 mm/d范围,平均下沉速率1.4 mm/d,顶板未出现加速蠕变。可见,两帮支护后顶板最大下沉速率由原来的3.2 mm/d下降为2.2 mm/d,巷道顶板下沉在40 d后趋于稳定,顶板处于稳定蠕变。
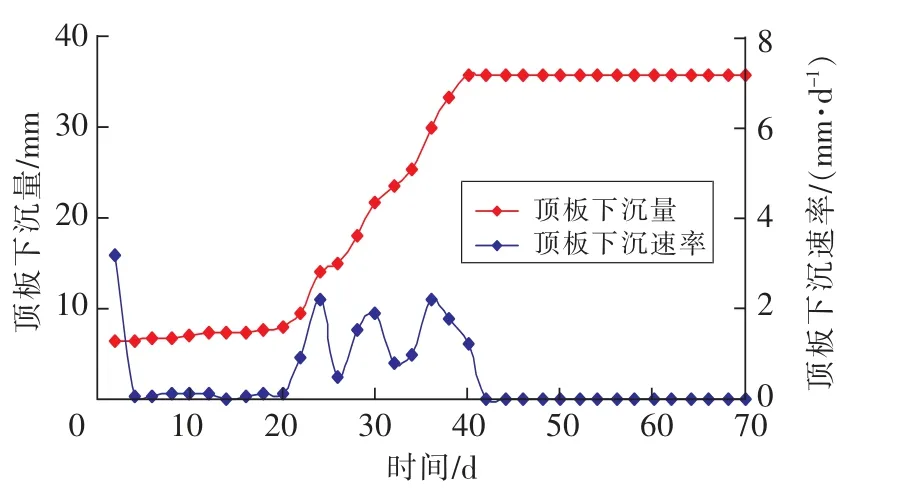
图16 巷道两帮滞后支护时顶板下沉蠕变Fig.16 Roof subsidence creep of headgate with two ribs lag support
4.3 工程实践
根据上述研究,14213胶带运输巷的最大滞后支护时间为掘进后28 d。张家峁煤矿据此进行巷道掘进支护实践,现场支护如图17所示。

图17 巷道顶板和帮部支护现场Fig.17 Site of headgate roof and two ribs support
根据4-2煤层14213胶带运输巷顶板离层仪3#测点观测情况,如图18所示,该巷道自2021年2月至9月,顶板离层仪深部基点观测数据最大值为12 mm,顶板离层量很小;实测巷道两帮移近量小于30 mm,无片帮情况,巷道围岩稳定。实践表明,采用合理的两帮滞后支护,提高掘进速度,促进工作面安全高效开采。
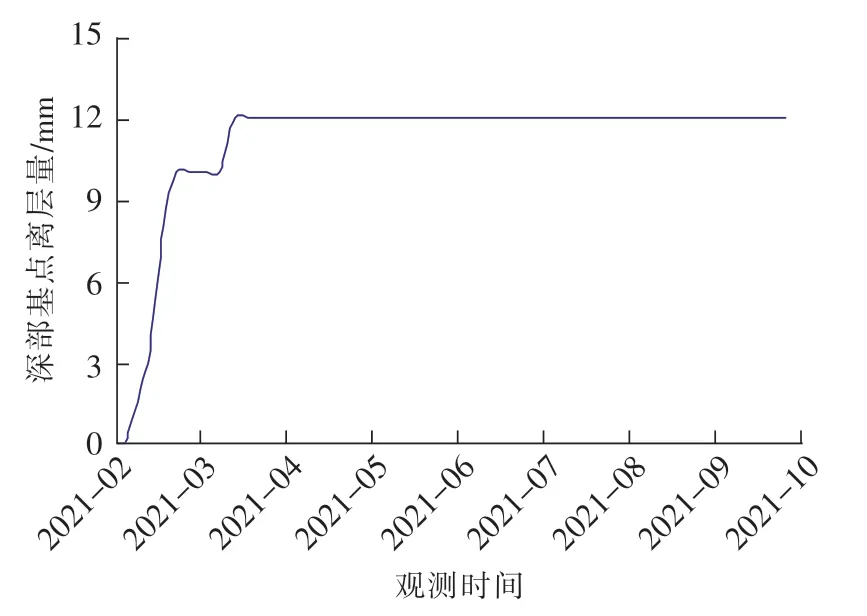
图18 顶板离层仪3#测点深部基点离层量Fig.18 Quantity of abscission at the deep base point of 3#measuring point of the roof abscission instrument
5 结 论
1)根据张家峁煤矿14213胶带运输巷断面及围岩条件,通过松动圈理论和等效圆法,得出矩形巷道两帮松动范围为52 cm,巷道两帮属于较稳定围岩,可以通过两帮滞后支护,提高掘进速度。
2)根据围岩蠕变规律,合理的滞后支护应当在围岩加速蠕变之前进行,以保障巷道安全。
3)张家峁煤矿14213胶带运输巷顶板及时支护两帮无支护时,28 d内两帮处于稳定蠕变,29 d后出现加速蠕变,两帮滞后支护需在28 d内进行;巷道两帮滞后28 d(加速蠕变前)进行支护,两帮移近速率下降55%,两帮移近量下降67%,未出现加速蠕变,滞后支护安全。
4)合理的两帮滞后支护,可保障巷道安全,有效提高巷道掘进速度。
