复杂山区地形滑雪场区域风环境数值模拟

贺佳伟,赵亚哥白,张洪福,辛大波

(东北林业大学 土木工程学院, 黑龙江 哈尔滨 150040)

0 引言

滑雪场是提供高山滑雪、跳台滑雪、越野滑雪等竞技滑雪运动的体育场地,通常有赛道、运输索道、服务场馆等基础设施。风场条件是运动员成绩和滑雪场安全运营的主要影响因素之一,主要体现在2个方面。首先,运动员赛训成绩受到风速和风向的影响。其次,运输索道的运行也受到风场环境的限制。滑雪场建设选址大多数为山区,滑雪场区域山丘起伏,沟壑纵横,增加了滑雪场区域风场的复杂性,使得地处滑雪场区域的赛道、索道等基础设施所受风的影响具有较强的不一致性。因此,开展复杂山区地形滑雪场区域风环境研究,精确地评价滑雪场区域的风环境,对于提高赛训质量,保障安全运营具有重要意义。

开展复杂地形风场研究手段通常包括现场实测、风洞试验和CFD(computational fluid dynamics, CFD)数值模拟。现场实测是获取风场信息的最有效手段[1-4],可以准确地分析风速谱、湍流强度、阵风因子、湍流积分尺度等脉动风特性。例如黄国庆等[5]通过在宣威方向桥位处附近建设测风塔,安装数据采集系统,实现了普立特桥位处风特性的实测研究。风洞试验通过制作真实地形的缩尺模型,根据试验目的合理布置监测点来获取监测位置的风特性参数。例如YAMAGUCHI等[6]利用风洞试验获取平均风速和湍流度等,研究了日本沿海地区复杂地形下的气流特性。胡峰强[7]以贵州北盘江大桥和湖北四渡河大桥周边的地形为工程实例,结合风洞试验结果以及附近气象台的数据资料,提出了复杂地形桥址地区设计基本风速梯度的修正方法。由于现场实测成本较高,需要长时间的数据采集,对仪器设备野外工作的性能有很强的要求[8],而风洞试验受实验室条件的限制,地形模型缩尺比较大时,会出现雷诺数效应,CFD数值模拟具有省时、经济、高效的特点,因此,CFD数值模拟技术成为研究复杂地形风场特性的重要手段[9-11]。随着CFD技术在复杂地形风场模拟的广泛应用,在各方面的研究已取得很多进展。在复杂地形建模方面,胡朋等[12]和刘志文等[13]通过建立地形过渡段来消除来流风经过地形截断边缘出现的分离和绕流等现象,减小“人为峭壁”对数值模拟的结果影响。在模拟区域范围大小及网格划分方面,张希斌[14]研究了复杂地形范围大小对数模拟的影响。肖仪清等[15]、周志勇等[16]和CHAO等[17]通过设计多种网格方案来确定最优网格最优划分方式。在数值模湍流模型的选取方面,TANG等[18]采用开源CFD软件OpenFOAM, 应用基于雷诺平均 Navier-Stokers(RANS)方程和修正的k-ε湍流模型,实现了高分辨率的风资源分布和准确的风速估算。HUANG等[19]基于平衡大气边界层模拟获取入口边界条件,用SSTk-ω模型对香港小蚝弯观测站周围的复杂地形进行多风向数值模拟,并与风洞试验和观测数据进行对比,验证数值模拟的准确性。

综上,近年来开展复杂地形风环境研究主要集中在工程建设选址、风能资源评估等方面,开展滑雪场区域风环境的研究较少。文中利用数值模拟方法针对亚布力滑雪场所在区域开展风环境研究,分析了滑雪场赛道区域、索道位置风场特点,并对赛训和索道运营安全提出建议。

1 数值计算模型

1.1 工程概况

黑龙江亚布力滑雪场地处于山地林区,是我国重要的滑雪比赛及训练基地,雪场及设施建设具有典型的代表性。针对滑雪场区域地形的特点,从地形图上选取滑雪场中心半径为3 km范围的地形。在此地形中包括1.2 km滑雪赛道和长800 m运输索道,A～E为现场风速仪的安装位置,滑雪场区域平面如图1所示。雪场周围具有数量众多的高海拔山峰,风场环境具有高度的复杂性,滑雪场周边高程如图2所示,M1～M4为周边山体,E为风速仪位置。

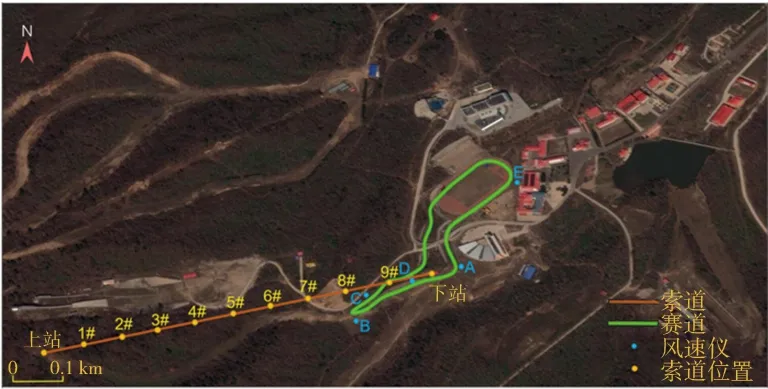
图1 滑雪场区域平面图Fig. 1 Plan of ski resort areas

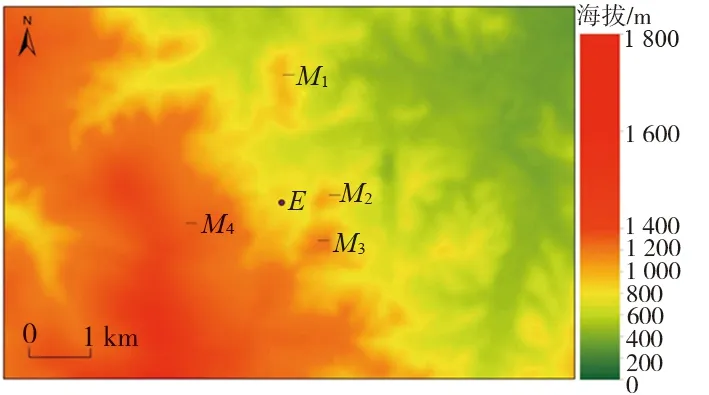
图2 滑雪场周边高程图Fig. 2 Elevation map around the ski resort

1.2 计算模型及网格划分

针对图1的地形范围,高程数据采用全球数字高程模型(ASTER GDEM),分辨率为30 m。考虑到地形数据直接建模会出现截断高差,通过HUANG等[20]提出的地形过渡曲线建立过渡段来减小“人为峭壁”的影响,如图3所示。过渡曲线如式(1):

图3 地形过渡段Fig. 3 Terrain transition surfaces

(1)

式中,x、y为归一化处理之后的过渡曲线的长度和高度,根据式(1)通过地形边缘的高程就可以得到地形过渡段的长度。

为了确保来流风得到充分发展,根据FRANKE等[21]对数值模拟计算域的建议,入口距离地形中心的距离为5.5D,地形中心距出口距离为10.5D, 地形中心距两对称边界的距离为5.5D,D是模拟地形的直径6 km,计算域的高度Hd为7 km。计算域的尺寸为16D×11D×Hd, 地形模型阻塞率小于3%,满足规范要求。

整个计算域分成3个部分,包括:外围区域、空心圆柱过渡区域和内部圆柱地形区域,如图4所示。

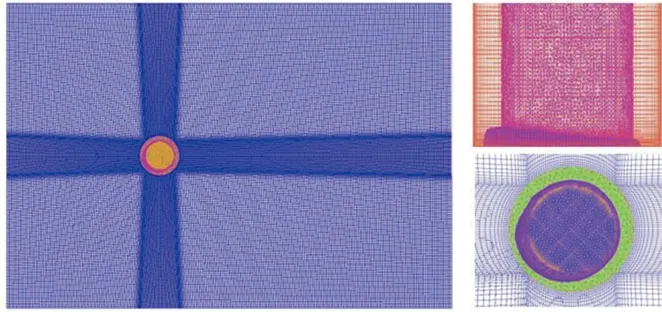
图4 计算域网格划分Fig. 4 Computational domain meshing

采用四面体和六面体网格混合的划分方法,外围区域由于关注来流和尾流发展的阶段,选择结构化六面体网格。过渡区域及地形区域,由于曲面不规则,采用非结构化的四面体网格。考虑到地形的复杂性,在近地面边界层设置5层棱柱体网格,第1层网格高度为1 m,增长因子为1.1。Uf为入口10 m高度位置的风速(m/s),U为测点距离地面高度的风速(m/s),图5为877万、628万、533万的3种不同数量网格下,风速仪E位置的无量纲化风速剖面模拟结果。3种不同数量网格下风剖面几乎完全重合,这表明文中计算结果与网格数量无关。为节约计算资源,在文中均选取533万的网格模型进行滑雪场风环境的数值模拟研究。

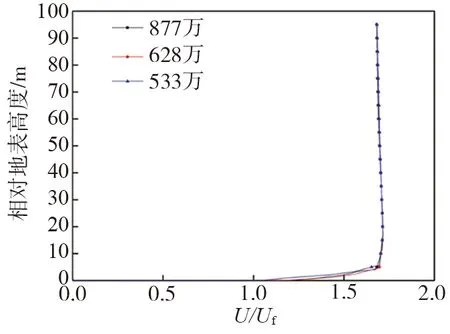
图5 网格无关性验证Fig. 5 Independence analysis of grid resolution

1.3 边界条件与计算参数设置

计算域内地形的粗糙度会对风速的垂直分布产生较大的影响,它在很大程度上决定了区域内的局部流动条件和近地面边界层的发展[22]。Fluent在处理壁面函数时,是通过将粗糙度长度z0转换为粗糙度物理高度ks进行设置[23],粗糙度长度和粗糙度物理高度之间存在的关系为:

(2)

式中:Cs为粗糙度常数,通常取0.5;根据地表粗糙度分类的划分[24-25],有少量的树或建筑的城镇,本研究中地形区域的地表粗糙度长度z0设为0.03 m。

计算域的上方和2个侧面设置为对称边界条件,底面过渡区域及地形采用无滑移边界条件,出口为压力出口(pressure-out)。计算域入口通过用户自定义函数(UDF)进行编译,速度入口表达式为式(3),按我国规范的大气边界层B类地表风剖面规律(指数α为0.15)进行设置,湍动能k及耗散率ω的入口条件[20]如式(4)、式(5)所示:

(3)

(4)

(5)

式中:Ux表示地面高度z处的风速(m/s);Ur表示参考高度zr处的风速;湍流强度I取5%,湍流积分尺度l取500 m; c为常数0.033。

湍流模型选用对流动分离解析度较好的k-ωSST剪切应力模型[26],压力与速度耦合处理选SIMPLEC算法。梯度插值方法为Green-Gauss Node Based,动量、湍动能、耗散率的控制离散格式采用二阶迎风(second order upwind),压力基非稳态求解器,计算时间步长为0.1 s,总体残差设为10-6,当速度迭代不再随时间波动,认为计算收敛。

1.4 计算工况与观测点设置

选取12个来流风向(见图6),定义0°为正北风向,来流风的角度顺时针旋转为正,每30°为1个工况,工况1～12的来流风向为0°～330°。滑雪场赛道区域地势处于地形的凹段,选取风速仪E海拔高度处的平面风速,研究不同来流风向下地形对滑雪场赛道区域风环境的影响。

图6 风向工况示意Fig. 6 Sketch of wind direction cases

为了得到索道处风环境特性,在索道缆车行进方向上站与下站之间等距布置9个观测点,观测点距地表高度约10 m,索道下站到上站地势逐渐升高,上站与下站高程差约200 m,如图7所示。 通过计算不同来流风下风速放大系数、风攻角、风偏角来获取索道行进方向各观测位置处的风环境特性。风速放大系数定义为山体某一高度风速的平均值与入口处同一高度处风速的比值,用以量化山体对来流风速的放大作用。

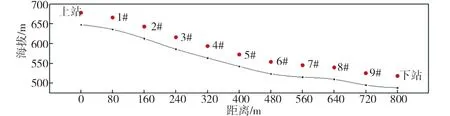
图7 索道观测点布置示意Fig. 7 Sketch of ropeway observation points layout

风速放大系数Cu、风攻角α、风偏角β的计算表达式见式(6)～式(8):

(6)

(7)

(8)

式中:U为索道观测点位置的风速;Uf为入口10 m高度位置的风速;Uu、Uv、Uw、分别代表纵向、横向、竖向的风速分量。

1.5 CFD数值结果验证

基于前述的网格及相应的边界条件,在山体前选取某一位置来绘制风速剖面,对来流风进行了自保持分析,从图8中可以看出,山前与入口风剖面几乎重合,说明风速具有较好的自保持性。

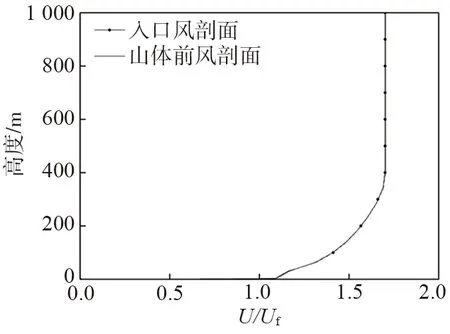
图8 风剖面自保持性验证Fig. 8 Self-preservation verification of wind speed profile

图9给出了来流风经过地形过渡段后的流场情况,来流风在地形过渡段边缘风速开始减小,经过地形过渡段后气流有一定的缓慢抬升,当气流到达地形中间区域时风速已基本保持来流风速的大小,表明地形过段曲线应用于山区风场建模具有较好的过渡性能,数值模拟结果具有可信度。

图9 地形过渡区风速云图Fig. 9 Wind speed contour of the terrain transition areas

为了验证CFD数值模拟的准确性,根据图1中各风速仪采集的数据,将CFD数值模拟结果与现场实测的风速及风向进行对比。定义2组风速比:

1)定义标准风速比K,K是测点位置的风速与参考点位置风速的比值。由于风速仪C的安装位置海拔较高,风速受周围地形地势的影响较小,选取风速仪C的位置作为参考点,如式(9)、式(10)所示:

(9)

(10)

式中:Kexp、Knum为实测风速比和模拟风速比;Wi、Vi为风速仪i位置的实测和数值模拟的平均风速;WC、VC为风速仪C位置的实测和数值模拟的平均风速。

2)定义水平风速比KH,KH是某海拔高度处局部水平风速与模拟入口10 m高度处风速的比值,如式(11)所示:

(11)

式中:VH为海拔高度为H的局部水平风速;V10为远方来流入口10 m高度处的平均风速。

观测点C一个月(2019年12月)的现场实测风向统计结果如图10所示,平均风向大多在90°～240°。现场实测数据选取10 min平均风速数据,6个风向下的模拟风速比与实测风速比如图11(a)所示。

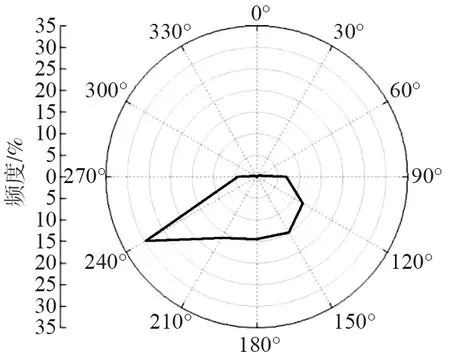
图10 风速仪C现场实测风向分布频度Fig. 10 Frequency of wind direction distribution measured on site by anemometer C

从图11(a)中可以看出,模拟风速比Knum与实测风速比Kexp的误差基本在20%以内,表明模拟与实测对应方向的风速比具有良好的一致性。图11(b)为数值模拟风向(PHInum)对应的现场实测方向(PHIexp),模拟风向与现场实测的偏差小于15°。

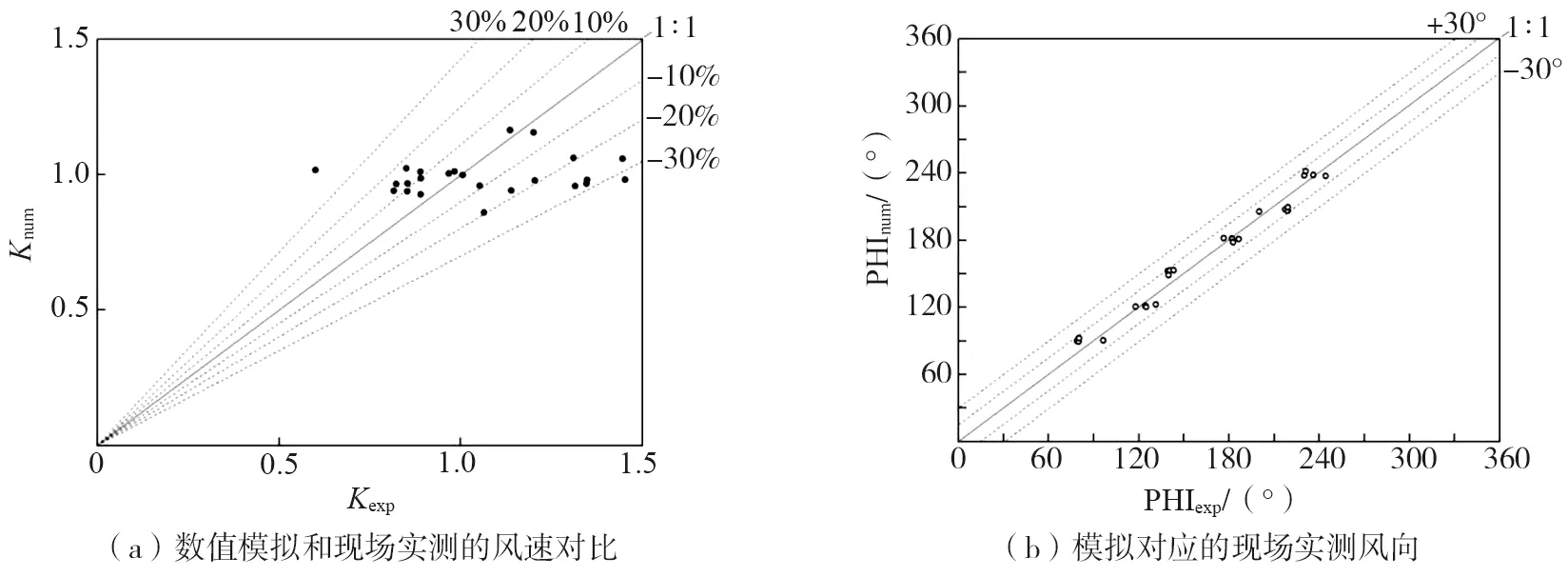
图11 数值模拟结果与现场实测对比Fig. 11 Comparison between numerical simulation results and field measurements

来流风向分别为90°和180°,海拔高度为532 m的风速仪位置周边区域的模拟风速比如图12和图13所示。入口风向为90°时来流风从开阔地带向山谷地区靠近,风速逐渐减小。来流风向为180°时研究区内风速会受到高山影响,风速先减小后增加。数值结果符合该研究区地形风场的常规分布特征,表明数值模拟具有一定的准确性。

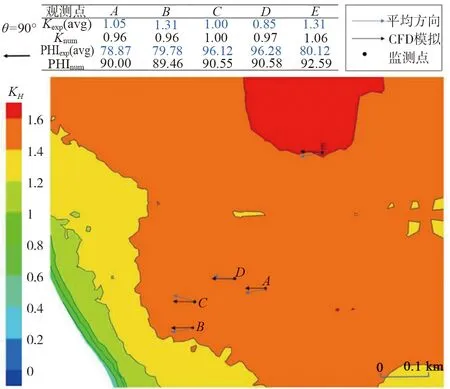
图12 风速仪位置周边区域KH云图(来流风向90°,海拔高度532 m)Fig. 12 KH contour of the surrounding areas of the anemometer (incoming wind direction 90°, altitude 532 m)

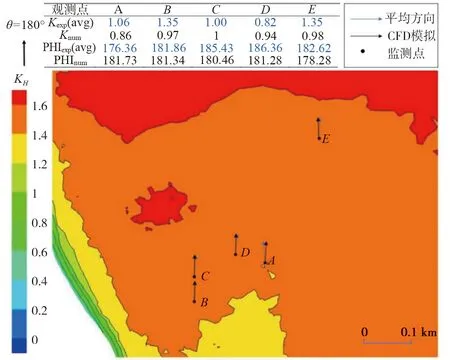
图13 风速仪位置周边区域KH云图(来流风向180°,海拔高度532 m)Fig. 13 KH contour of the surrounding areas of the anemometer (incoming wind direction 180°, altitude 532 m)

2 雪场区域数值模拟的应用

2.1 滑雪赛道风场分析

E点周围的风速场分布如图14所示,图中黑色箭头表示风的流动方向,云图中地形范围白色区域是山体在海拔高度为505 m处的截面。

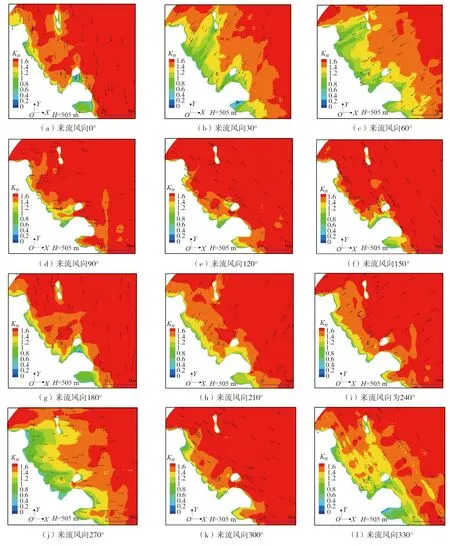
图14 E点周围的KH云图Fig. 14 KH contour of the surrounding areas of the point E

当来流风向为0°时,来流风在山体M1和M4之间出现加速,之后风速开始衰减,在到达赛道E点附近出现风速增大现象。来流风角为30°和60°时,山体M1和M2对来流风起到了阻挡作用,来流风到达赛道附近观测点E时风速相应的减小。来流风向角为90°和120°时,来流风经过山体M2和M3出现峡谷风效应,风速在2个山峰之间加速,之后平缓地过渡到观测点E。来流风向为150°和180°时,来流风经过2个山体,到达E点附近经历了2次折减。来流风向角为210°、240°、270°和300°时,来流风主要受山峰M4的影响,风向角为270°时阻挡影响较大,观测点E附近的风速最小。风向角为240°、270°和300°时,来流风均在山体M2和M3之间出现峡谷加速效应。来流风向为330°时,山体M1和M4对来流风起到了阻挡作用,来流风到达赛道附近观测点E时风速逐渐减小。风的流动方向会受到邻近山体的影响,在来流风270°较为明显。整体上看,来流风向为30°、60°、270°和330°时,滑雪场邻近山体对来流风的阻挡效应最大,赛道处的风速较小,适宜正常开展比赛及训练。

2.2 索道位置处风环境评价

索道各位置的风速会受到邻近山体的影响,从图15中可以看出,除来流风向为270° 外,来流风速经过复杂地形后,索道各观测位置的平均风速放大系数Cu基本大于1,风速整体增大。总体上,索道各观测位置风速均受地形地势条件的影响,地势较高的观测位置处的Cu整体大于地势较低位置处的Cu,但6#观测点的Cu最小,1#位置的Cu最大。因此,可将1#观测点位置的风速作为索道安全运营的阈值风速,当此观测点风速超过索道的安全限值风速20 m/s时[27],应停止索道的运行。来流风向为0°时,索道各观测点的Cu最大。来流风向为270° 时,各观测点的Cu最小,分析结果与前文2.1节中地形对滑雪场区域风场的影响基本一致。

风攻角是影响缆车气动力系数的重要参数,也是结构抗风设计中考虑的重要因素[28-29]。由图16可见风攻角呈180°对称分布,来流风向为0°～150°时,气流从低海拔流向高海拔地区,会出现“爬坡”现象,索道1#～9#位置产生正向的风攻角。来流风向为180°～330°时,来流风越过山顶后尾流产生向下的风速分量,气流出现“下坡”现象,索道1#～9#位置产生负向风攻角。总体上看,各工况索道上站到5#观测点位置的风攻角较大,这是因为上站到5#观测点位置之间的海拔较高,地势与周边平坦地区相比起伏大,地形地势对气流的影响显著,产生较大的风攻角。而6#观测点到索道下站位置之间的海拔相对较低,地势相对平坦,风攻角较小。在该滑雪场抗风设计中,要考虑风攻角对索道上站到5#观测点位置之间产生的不利影响。

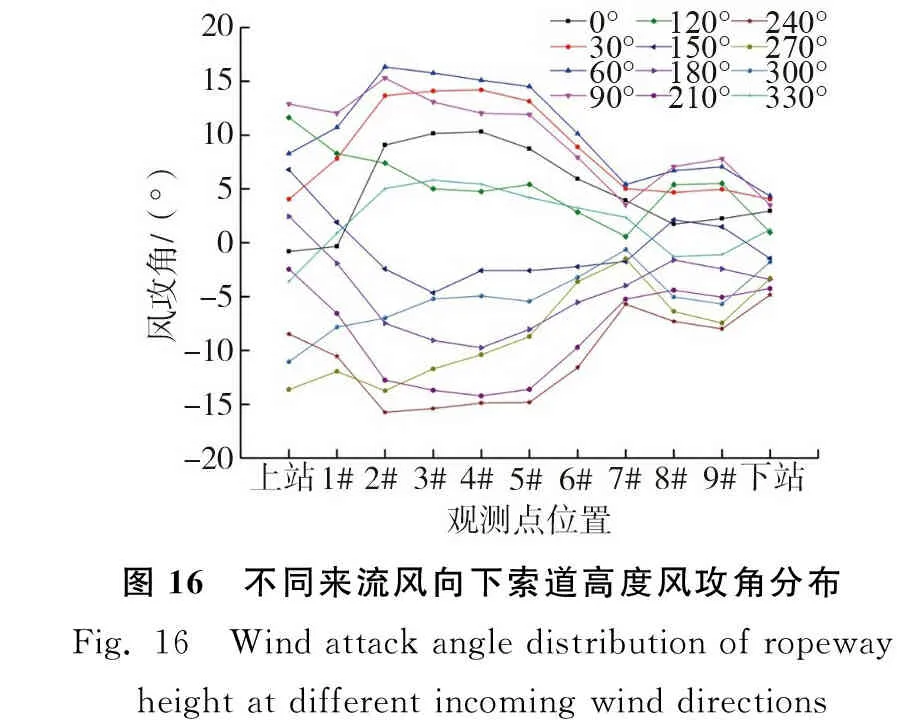
图17列出了不同来流风向下索道高度观测位置的风偏角分布。来流风向为270°时,5#观测点到索道下站位置之间的风偏角较大,除此来流风向外,风偏角变化较大的位置均在索道上站到3#位置之间,5#～7#位置由于受局部地形的影响,风偏角变化也相对较高。由图1可知,4#位置由于受到周围地形地貌的影响各来流风向下风攻角变化均较小,总体上看,索道位置地势越高对气流的流动方向影响越大。风偏角对索道缆车的行进安全有重要的影响,根据GB 50127—2020《架空索道工程技术标准》[30]风速大于5 m/s横向摆动一般小于0.24 rad(约13.75°)时不离开承载索。来流风向为330°时的索道上站到3#位置,以及来流风向为270°时,5#位置到索道下站位置,风偏角均大于13.75°,当风速大于5 m/s时,应考虑风偏角对索道安全运行的影响。

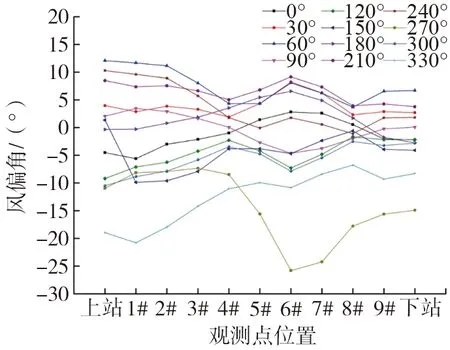
图17 不同来流风向下索道高度风偏角分布Fig. 17 Wind yaw angle distribution of ropeway height at different incoming wind directions

3 结论

以亚布力滑雪场为工程背景,利用三维地形建模及CFD模拟方法,研究了地形对滑雪场赛道风场的影响以及滑雪场索道区域风空间分布特性,主要结论如下:

1)文中采用地形过渡曲线对山区地形进行建模,利用组合网格划分方式,通过壁面函数方法对研究区进行CFD数值模拟。数值模拟结果与现场实测的偏差基本在20%以内,CFD数值模拟方法具有一定的准确性,能够满足复杂地形滑雪场区域风特性研究的要求。

2)基于该方法可以有效地开展亚布力滑雪场赛道风场分析,来流风向为30°、60°、270°和330°时,滑雪场邻近山体对来流风的阻挡效应最大,赛道处的风速较小,适宜正常开展比赛及训练。

3)该数值方法可以模拟评价亚布力雪场索道风环境,索道各观测位置的平均风速放大系数Cu基本大于1(来流风向270°除外)。1#观测点位置的风速可作为索道安全运营的阈值风速。风攻角和风偏角均受地形地势的影响,风攻角较大的位置出现在索道上站到5#观测点之间,风偏角变化较大的位置出现在索道上站到3#观测点之间。