基于改进MPC 算法的四旋翼无人机轨迹跟踪控制

张鑫 吴伊凡 崔永琪

（航天工程大学 北京市 101416）

四旋翼无人机可以携带各种设备，具有结构简单、机动性强等特点。可广泛应用于军事、商业、农林牧等领域。然而，该系统具有欠驱动、强耦合、非线性等特性。为此，国内外许多学者提出了各种算法来针对四旋翼无人机的飞行控制问题，包括PID算法[1]、模型预测控制[2]、滑模控制[3]、自抗扰控制[4]等。上述控制算法可以使四旋翼无人机控制系统保持稳定。然而四旋翼无人机在实际飞行中受风干扰的影响较大，会对机体本身造成损坏，维护成本高[5]。

综上所述，针对风扰对四旋翼无人机轨迹跟踪控制影响这一问题，本文提出了一种结合MPC 和ESO 算法的轨迹跟踪控制方法，所设计的控制器采用内外环控制结构，外环位置控制器与内环姿态控制器均采用MPC和ESO 结合的方法，该控制器旨在实现在风扰动情况下四旋翼无人机的精确轨迹跟踪控制。仿真结果表明，与自抗扰控制相比，本文所设计的控制器有更小的稳态误差和更强的抗干扰能力。

1 风扰下四旋翼无人机动力学模型

四旋翼无人机在飞行过程中会受到许多因素的影响，这样会使得四旋翼无人机的动力学模型会比较复杂。针对这种情况本文作出以下一些合理的假设：

（1）将四旋翼无人机视为刚体，机体坐标系原点与质心重合，在运动过程中质量保持不变。

（2）忽略旋翼在运动过程中产生的弹性形变。

（3）四旋翼无人机飞行过程中姿态角变化较小，适用于小姿态角假设。

（4）四旋翼无人机旋翼产生的升力与旋翼转速的平方成正比[6]。

1.1 四旋翼无人机空气动力学分析

自然界的风主要为突风，紊流，风切变等，实际上这些类型的风不会单一出现。针对四旋翼无人机飞行所处的环境，主要考虑了紊流风场的影响。本文采用结构简单且适用的Dryden 紊流风场[7]来描述。四旋翼无人机在运动过程中受到紊流风场的扰动是不可避免的，这使得四旋翼无人机的控制器设计需要考虑抵抗这种干扰。因此分析紊流风场对四旋翼无人机的位置平动和姿态转动的影响[8]，可以更方便准确的建立四旋翼无人机动力学模型。

对四旋翼无人机中的一个旋翼在紊流风场下进行受力分析，如图1 所示。

图1 中，Vw为风速，Vd为诱导速度，为合速度。这三个速度方向的关系如下：

旋翼产生的诱导速度可以由下式给出：

式（2）中，ρ为所处环境的空气密度，Fi为旋翼产生的升力大小。A为旋翼桨叶扫过的面积。

在外部风场中，旋翼产生的总升力FR是旋翼的拉力Fi与风产生的升力FW的矢量和，如下式：

由式（1）、（2）、（3）可得FW为：

紊流风场作用下，旋翼产生的总空气力矩MR可由下式计算：

式（5）中，kd＞0 与旋翼形状以及空气密度等因素有关。

1.2 紊流风场下的四旋翼无人机动力学模型

四旋翼无人机的运动过程是由刚体的平动和绕质心的转动组成，在地面坐标系下建立平动方程，在机体坐标系下建立转动方程，根据牛顿-欧拉方程，得出下式：

式（6）中，m 为四旋翼无人机的重量，ζ=[xyz]T为无人机质心的位置坐标，F为无人机受到的合外力，I=diag(Ix,Iy, Iz) 为惯性张量对角矩阵，η=[pqr]T为无人机三个旋转角对应的角速度，τ为无人机受到的总合外力矩[9]。

四旋翼无人机产生的总升力U1为四个旋翼产生的升力之和，其表达式如下：

四旋翼无人机是轴对称结构，四旋翼无人机在运动过程中会产生滚转力矩U2、俯仰力矩U3以及由于反扭矩产生的偏航力矩U4，其表达式为：

式（8）中，l表示四旋翼无人机的质心到旋翼中心的水平距离，表示第i旋翼转速的平方值，λ为升力系数，μ为扭力系数。

四旋翼无人机在飞行过程中，产生的陀螺力矩的表达式为：

式（9）中，Ip为旋翼的转动惯量，ωT=-ω1+ω2-ω3+ω4为旋翼的相对转速。

由式（6） ～ （9）可得，四旋翼无人机在紊流风场下的动力学模型为：

式（10）中U=[U1U2U3U4]T为虚拟控制量，f=[fx fy fz fφ fθfψ]T为四旋翼无人机受到的风的扰动量，具体表达式见文献[10]。

2 四旋翼无人机控制器设计

2.1 MPC-ESO控制算法构建

为了使四旋翼无人机在紊流风场的干扰下更精确的跟踪参考轨迹，本章控制器是基于MPC-ESO 算法设计的，采用内外环结构，对应的四旋翼无人机控制结构示意图如图2 所示。

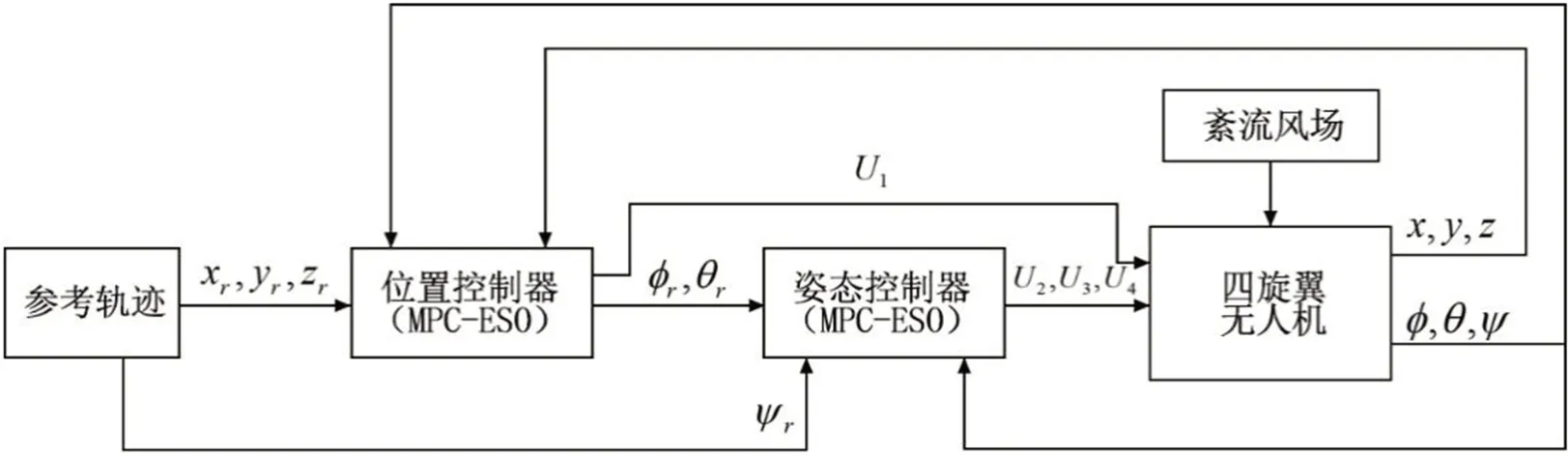
图2：四旋翼无人机控制结构示意图

其中xr，yr，zr和ψr是给定的参考轨迹，U1是位置控制器得到的控制输入量，φr和θr是位置控制器得到的欧拉角参考值，U2、U3和U4是姿态控制器得出的控制输入量。

2.2 四旋翼无人机控制器设计

2.2.1 位置控制器设计

2.2.2 姿态控制器设计

3 仿真结果与分析

本文通过MPC-ESO 的方法设计了位置控制器和姿态控制器，为了验证该控制器在轨迹跟踪控制方面的性能，在建立四旋翼无人机在紊流风场下的动力学模型的基础上，将本文提出的控制器与自抗扰控制系统进行仿真对比验证。

本文设定四旋翼无人机的初始位置为x0=0.5，y0=0，z0=0.5，初始姿态为φ0=0，θ0=0，ψ0=0。四旋翼无人机的参考轨迹为

四旋翼无人机在风扰动条件下利用设计的控制器进行跟踪控制模拟仿真，四旋翼无人机在三维空间的轨迹跟踪效果图如图3 所示，并与自抗扰（ADRC）轨迹跟踪控制系统进行比较，结果如图4、图5 与图6 所示。

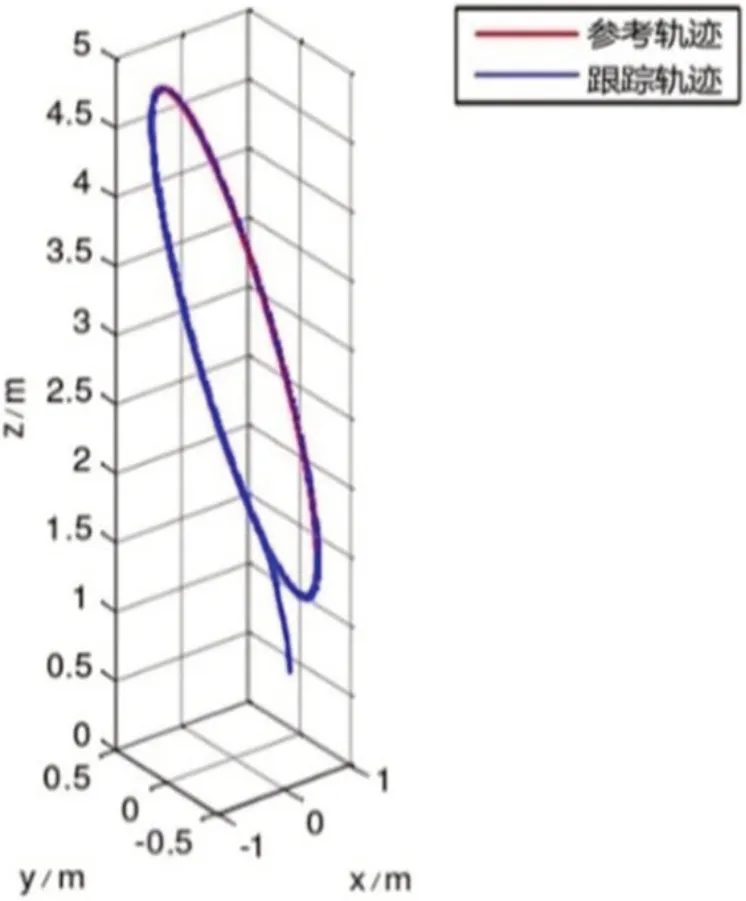
图3：三维轨迹跟踪仿真图

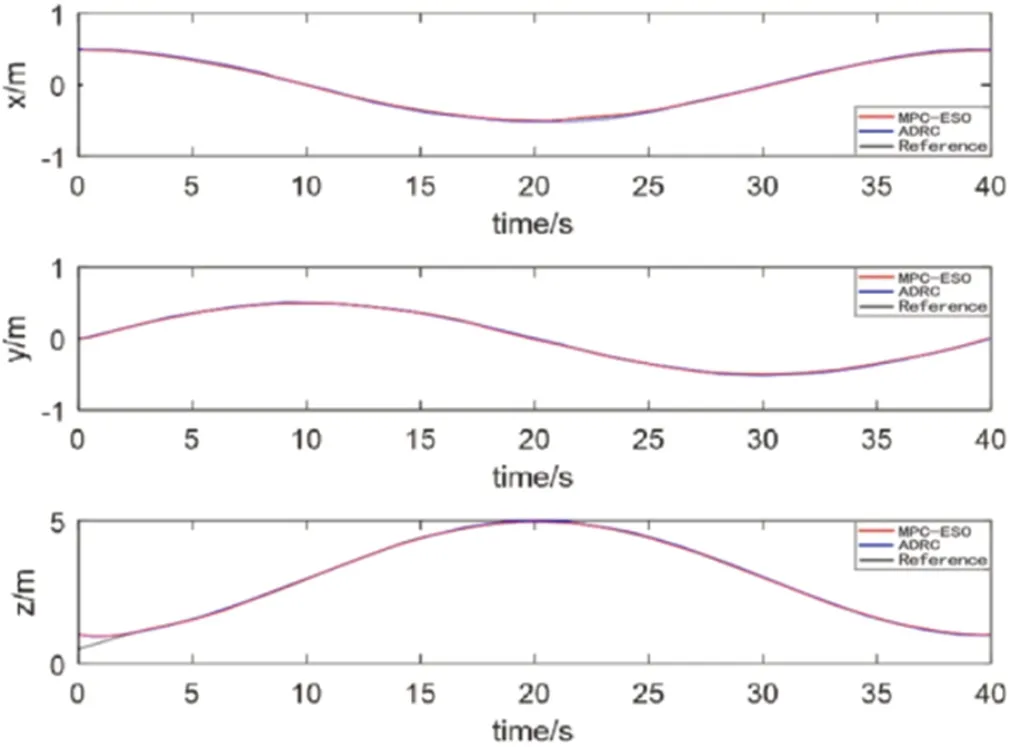
图4：位置跟踪控制曲线

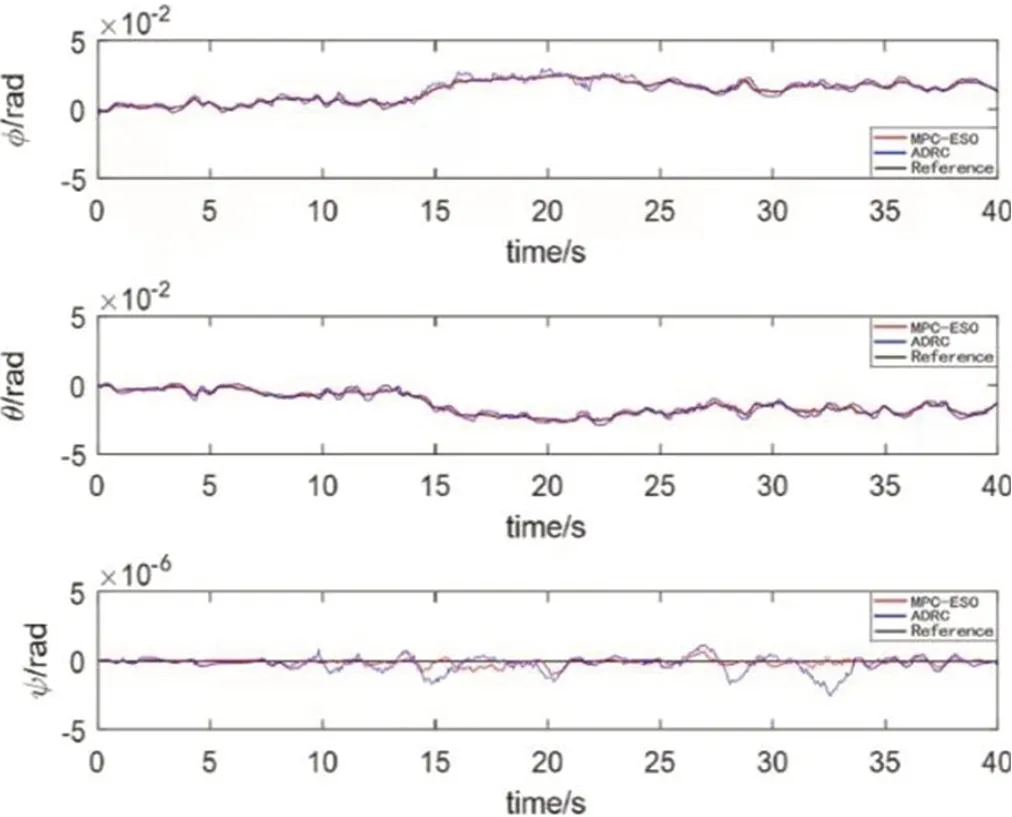
图5：姿态跟踪控制曲线

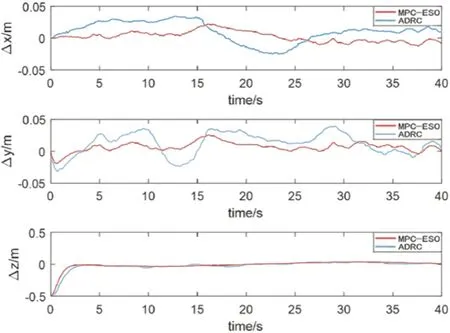
图6：轨迹跟踪控制误差曲线

由以上结果图可知，在受到风场干扰的影响以及初始位置不在参考位置上的情况下，提出的控制器仍能够使四旋翼无人机精准跟踪参考轨迹，并且实现了姿态控制，能较快的达到设定值并保持稳定，实现了姿态的快速响应，提高了风扰影响下四旋翼无人机轨迹跟踪控制品质。与ADRC 控制器相比，MPC-ESO 控制器跟踪误差更小，抗干扰能力更强。

4 结论

四旋翼无人机在实际飞行过程中避免不了风扰的影响，为实现四旋翼无人机飞行控制系统在风干扰下的快速响应和可靠控制，提出了一种MPC-ESO 算法的飞行控制策略。所设计的控制器采用双闭环控制结构，其能够保证四旋翼无人机在风扰动条件下的稳定运行，在飞行过程中能够精准的跟踪参考轨迹，提高了控制系统的稳定性与跟踪性能。