人工智能在船舶航行数学建模中的应用
2023-05-14赵珈玉鞠岩松
白 灵,赵珈玉,鞠岩松
(1. 长春电子科技学院 光电科学学院,吉林 长春 130000;2. 长春理工大学 化学与环境工程学院,吉林 长春 130000)
0 引 言
船舶在航行过程中,会遇到海面勘探、石油开发等水域作业情况,为使船舶安全航行,规划其航行航线意义重大。杨琪森等[1]提出的船舶路径规划与避障方法,该方法通过构建马尔可夫决策过程抽象模型,通过深度强化学习算法,规划了船舶航行路径。谢新连等[2]提出复杂水域船舶路径规划方法,该方法建立环境模型,分析海浪对船舶速度的影响,利用改进粒子群算法优化船舶航行路径。上述2 种方法虽可实现船舶航线优化,但优化结果不够准确。人工智能算法也被称为机器学习算法,其包含寻优算法、识别算法等多种算法[3],是求解目标函数算法,可通过反复迭代输出最优解。面对当前船舶航线优化算法存在的不足,研究人工智能在船舶航行数学建模中的应用,为船舶导航提供技术支持。
1 基于人工智能的船舶航行数学建模
1.1 船舶航线规划数学模型构建
海上钻井平台或勘探区域作业通常包含多个水上、水下作业点,船舶在该区域航行时,受其作业点影响,威胁其航行安全[6],因此船舶航行时需规避海上不同作业点。
在建立船舶航线优化模型之前,使用Maklink 图论方法描述海上作业点分布,在海上作业水域建立Maklink 连接图,利用该图描述船舶在作业水域内可航行网络图,并将其表述为可求解的数学模型。令S和T分布表示船舶航行起点和终点,在点S和T之间的航线点序列 {S,q1,q2,···,qk,T}构成,在该点序列内,排除船舶航行起点和终点之外,其中包含的点均存在转向的可能。当船舶航行速度为定值情况下,使用 θqi表示船舶在点位置的转向角, φmax表示船舶在其设计航速下的转向极限角数值。船舶在转弯时,需考虑其转弯半径[7],船舶航速为10 kn 时,其最小转弯半径和转向角参数如表1 所示。

表 1 船舶最小转弯半径参数设计Tab. 1 Parameter design of minimum turning radius of ship
令Vt表示船舶航行速度,R表 示大型船舶航道转弯半径,当船舶为10×104~15×104t 的大型货轮时,其航道转弯半径计算公式如下:

式中:θ 表示船舶在某个点的转向角度;L表示船舶长度。
在综合考虑船舶转向角度和转弯半径后,建立船舶在海上作业区域航线规划数学模型,其表达公式如下:
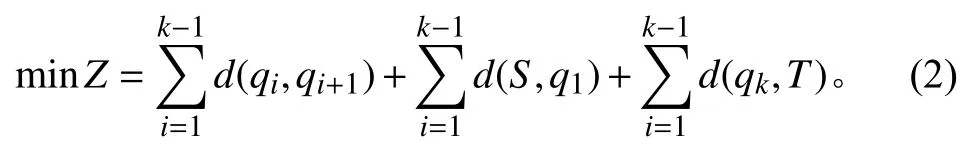
式中: minZ表示船舶在海上作业区域航线规划目标函数;(qi,qi+1) 为 由 点qi和qi+1两 点 组 成 的 航 线 段;d(·)表示航线点之间距离;(S,q1)表 示船舶起点S到q1航线点之间的航线段;(qk,T) 为船舶航线点qk到终点T之间的航线段。
令k表示船舶航行路径终点前的一个点,Z和Zmin分别表示航线与危险区域最小距离和最小安全距离。设置公式(2)约束条件为:
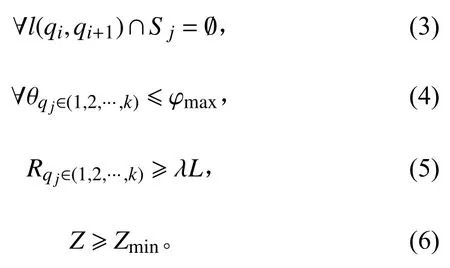
式中:l(qi,qi+1)表 示由qi和qi+1两点连接组成的航线点集,该点集与作业危险区域点集S j的交集为空集;船舶 航 行 时 节 点 θqj∈(1,2,···,k)的 转 角 需 小 于 φmax;λ表 示 船舶最小转弯半径和船舶长度比值。
经过上述步骤,完成船舶航线规划模型构建。
1.2 基于Dijkstra 算法的船舶航线规划模型求解
通过构建船舶在海上作业危险区域航线规划模型,利用Dijkstra 算法求解该模型,获得船舶在海上作业区域初始航线,其详细过程如下:
将求解船舶在海上作业危险区域航线规划模型问题转换成有向图最短路基问题[8],利用图论方式描述该模型,令W表示有向弧权值集合,则其船舶在海上作业危险区域航线规划模型图论表达公式如下:

式中:G表示船舶航线规划有向图;V=(v1,v2,···,vn)
表示航线有向图顶点集合;A表 示顶点之间有向弧集合。
利用Dijkstra 算法求解船舶在海上作业危险区域航线规划模型步骤为:
步骤1对航线有向图顶点V=(v1,v2,···,vn)赋予2 个标号 (U,E) ,U表示临时标号,该标号为实数,用于描述定点路径长度,E表示永久标号,描述有向弧的起始点。

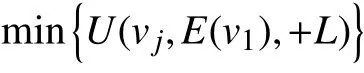
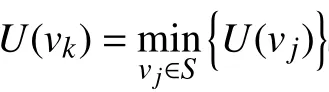
步骤5当vk=vn时 ,则得到航线点的最小距离E(vk)。
经过上述步骤,得到船舶在海上作业区域初始航线。
1.3 基于人工智能算法的船舶初始航线优化方法
使用Dijkstra 算法求解船舶在海上作业危险区域航线规划模型,得到其初始航线时,受航线点数量较多影响,其生成的初始航线无法满足船舶航行时的机动性能,因此以船舶在海上作业危险区域初始航线为基础,使用人工智能算法内的蚁群优化算法对船舶初始航线优化处理。
将船舶航行初始航线上的节点赋予初始值,生成初始信息素矩阵,其中危险区域节点的初始值为0,其他节点初始值为1。当时刻为t时,蚁群移动到线段Li位置。令第k只蚂蚁在点a(xi,yg) 位置,ηab(t)表示点a和b之 间的能见度,bj为线段Li+1上 的节点,ψ (j)为时刻为t时 ,节点j上残留的信息素。蚂蚁k在运动时,每个路径上的信息素决定其移动方向。在时刻为t时 ,蚂蚁k从a(xi,yg) 处转移到b(xi+1,yi)处的概率计算公式如下:

式中: α表示信息素相对重要性;ρkab表示蚂蚁k从a(xi,yg) 处 转 移 到b(xi+1,yi) 处 的 概 率;Ω 和 Ω′分 别 表 示航线安全区域和风险区域;β能见度相对重要性。
蚂蚁依据公式(7)概率搜索,在搜索过程中按照下式全局更新规则更新其行走路径:

式中: ϑ表示信息素蒸发因子;∆ ψ(j)表示全局更新因子,其计算公式如下:
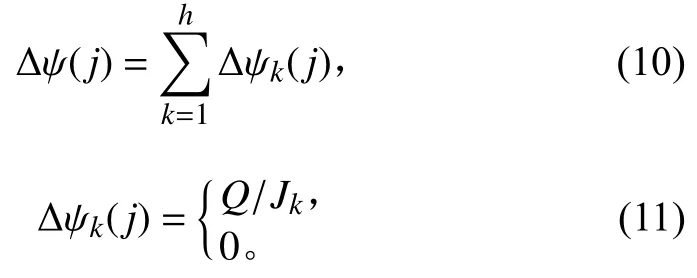
式中:h表示蚂蚁总数;Q表示常数;Jk表示蚂蚁搜索到可航行路径目标函数。
蚁群按照公式(9)更新其路径后,当迭代次数达到阈值次数,则输出当前路径,该路径即为优化后的船舶在海上作业区域航行路径,利用该路径为船舶导航,保障其安全航行。
2 实验分析
以某中型货运船舶作为实验对象,其需穿越海上石油钻井平台作业区域,其作业区域分布以及船舶航行起点位置如图1 所示。

图 1 海上作业区域与船舶航行起点Fig. 1 Offshore construction area and ship navigation starting point
2.1 作业水域可航行网络图
生成海上作业区域可航行网络图是获得船舶初始航线和航线优化的基础,使用本文方法获取海上作业区域,作业水域可航行网络如图2 所示。

图 2 作业水域可航行网络Fig. 2 Navigable network of construction waters
可知,本文方法可有效依据海上石油钻井平台作业区域得到船舶可航行线路,生成船舶可航行线路网络图,为后续得到船舶初始航线与初始航线优化打下良好基础。
2.2 船舶初始航线生成与航线优化
使用本文方法生成该船舶从起点到目的地航线,并对该航线优化处理,初始航线生成与航线优化结果如图3 所示。

图 3 初始航线生成与航线优化结果Fig. 3 Initial route generation and route optimization results
可知,使用本文方法可有效生成该船舶航行的初始航线,但该初始航线需要多次变更航向才可到达目的地,且生成的初始航线穿过7 号、8 号作业区域与11 号作业区域,该3 个作业区域呈三角形分布,中间航道较为狭窄,影响船舶航行航速。而使用本文方法对该初始航线优化后,优化后的航线仅需变更一次航向即可到达目的地,同时航行穿越作业区域时,其航道较宽,船舶可安全航行。综上结果,本文方法可有效生成船舶航行初始航线,并使用人工智能算法对其优化处理,具有较好的应用效果。
3 结 语
为了保证船舶的安全航行,研究人工智能在船舶航行数学建模中的应用方法。通过建立船舶航行数学模型并求解后,得到船舶航行初始航迹,通过人工智能算法中的蚁群算法,对其初始航迹优化,使船舶航行更加安全。通过对本文方法实际验证,其在生成船舶航线网络图,得到初始航线并优化方面均具备较好的能力,可用于船舶穿越海上作业区域导航,为船舶安全航行提供保障。
