基于动态矩阵控制算法的室内温度控制研究

单文啸, 李 科, 王睿鑫, 李卓阳, 丛铭阳,魏 存, 周志刚

(1.哈尔滨工业大学 建筑学院, 黑龙江 哈尔滨 150090; 2.寒地城乡人居环境科学与技术工业和信息化部重点实验室, 黑龙江 哈尔滨 150090; 3.中国工商银行数据中心, 上海 201800)

1 概述

提高供热质量、实现用户自主调控是智慧供热的目标之一[1]。由于室内供暖系统具有较大时滞性,传统室内温度控制方法(根据实测温度与设定温度的偏差来调节阀门开度)易出现室内温度调节不及时和室内温度超调的现象[2]。而采用预测控制的思想,预先计算室内温度与设定温度之间的偏差,提前对阀门进行调控,可以有效解决上述问题。

本文提出基于动态矩阵控制(Dynamic Matrix Control,DMC)算法的室内温度控制方法。将动态矩阵控制算法联合TRNSYS软件,建立散热器室内供暖系统仿真模型,对室内温度控制效果影响因素(用户调节阀流量特性、供暖时期、供水温度)进行分析。比较动态矩阵控制算法、PID控制、预测-反馈预测控制对室内温度控制效果。

文中的控制系统主要由控制器、被控对象、执行机构组成,其中控制器采用DMC算法,被控对象为室内温度,执行机构为用户调节阀。

2 DMC算法

DMC算法是一种预测控制算法[3]。该算法主要由预测模型、滚动优化、反馈校正3部分组成。先通过预测模型提前计算室内温度与设定值之间的偏差,然后通过滚动优化计算出下一时刻的最优控制量,最后通过反馈校正来校准预测模型。

2.1 预测模型

预测模型首先要获取对象的单位阶跃响应曲线a(t),并按指定的采样周期T给出各采样点的值ai=a(iT),i=1,2,…,n。这组对象的动态特性参数被称为预测模型向量a=(a1,a2,…,an)T,n为预测模型的建模时域长度。

单位阶跃响应是形容对象特性的一种非参数模型,由于线性系统满足叠加原理,因此可以使用单位阶跃响应参数来预测未来时刻的输出,并据此推导出预测模型:

在时间t=kT之前,控制系统保持稳态。

在t=kT时加入控制作用Δu(k),在t=(k+1)T时加入控制作用Δu(k+1),在t=(k+2)T时加入控制作用Δu(k+2),最后在t=(k+m-1)T时加入控制作用Δu(k+m-1)。控制系统稳定后,在t=kT时,在未来p个时刻的预测输出ypm(k)为:

ypm(k)=yp0(k)+ΑmΔum(k)

(1)

式中ypm(k)——t=kT时,在m个控制增量Δu(k),Δu(k+1),…,Δu(k+m-1)作用下,未来p个时刻的预测输出矩阵,p×1型

yp0(k)——t=kT时,无控制增量时未来p个时刻的预测输出矩阵,p×1型

Αm——DMC算法的动态矩阵,其元素由单位阶跃响应参数组成,p×m型

Δum(k)——从t=kT时起控制增量矩阵,m×1型

p、m——预测时域、控制时域,m≤p≤n

本文建立的预测模型为单输入单输出模型,输入为阀门开度,输出为室内温度。通过阀门开度变化对控制系统施加阶跃激励,待控制系统稳定后,可从温度变化曲线中提取阶跃响应数据,从而完成预测模型的建立。

2.2 滚动优化

DMC算法是一种以优化确定控制策略的算法。通过优化指标J(k)确定出不同采样时刻的未来m个控制增量Δu(k),Δu(k+1),…,Δu(k+m-1),使未来p个输出的预测值ym(k+1|k),ym(k+2|k),…,ym(k+p|k)尽可能接近期望值w(k+1),w(k+2),…,w(k+p)。

在t=kT时,优化性能指标可取为:

式中qi、rj——误差权、控制权系数

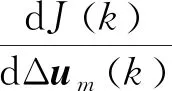
Q=diag(q1,q2,…,qp)

R=diag(r1,r2,…,rm)

式中Q——误差权矩阵,对角线元素为误差权系数qi,p×p型

R——控制权矩阵,对角线元素为控制权系数rj,m×m型

wp(k)——在t=kT时,未来p个时刻的输出期望值矩阵,p×1型

2.3 反馈校正

由于实际过程中存在模型失配与弱线性特性等不确定影响因素,为了纠正预测模型与现实之间的不一致性,需要利用过程的错误信息及时纠正输出预测值。为此,在t=kT时首先实施Δum(k)中的第1个控制增量Δu(k):

Δu(k)=cΔum(k)=d[wp(k)-yp0(k)]

c=(1 0 … 0)1×m

式中c、d——中间变换矩阵,分别为1×m型、1×p型

由于Δu(k)已作用于控制对象,控制系统未来的输出预测值yp1(k)要加上Δu(k)的影响,可由式(1)计算。在下1个采样时间t=(k+1)T,需要检测控制系统的实际输出y(k+1),并与预测模型计算的输出y1(k+1|k)进行比较,得出预测误差e(k+1):

e(k+1)=y(k+1)-y1(k+1|k)

式中e(k+1)——在t=(k+1)T时的预测误差

y(k+1)——在t=(k+1)T时控制系统的实际输出

y1(k+1|k)——在t=(k+1)T时预测模型的输出

预测误差反映了预测模型中的各种不确定性因素,则对控制系统的输出预测可以通过误差加权的方式进行校正。

ycor(k+1)=yp1(k)+he(k+1)

式中ycor(k+1)——在t=(k+1)T时经误差校正后所预测的控制系统在该时刻的输出

h——误差校正向量,用于修正模型

在t=(k+1)T时,由于时间基点的改变,预测的未来时间点也将移动到t=(k+2)T,t=(k+3)T,…,t=(k+p+1)T。因此,ycor(k+1)的元素还需要通过移位才能成为t=(k+1)T时的初始预测值,可用向量形式表示为:

yp0(k+1)=sycor(k+1)

式中s——位移变换矩阵

在t=(k+1)T时,有yp0(k+1),就可以再次进行新的预测、优化,整个控制过程就是这样滚动着进行的。

2.4 DMC算法特点

DMC算法本质上是对控制增量的一种计算方法,无论模型是否存在误差,它总是可以把控制系统输出值稳定到期望值附近。即使受到干扰,它也可以使控制系统的被控量恢复到设定值。综合来看,DMC算法有以下特点。

① 可以在算法中考虑控制系统的控制量、被控量的约束条件,在满足约束条件的情况下求出下一时刻的最优控制量。

② 把误差权矩阵Q、控制权矩阵R作为设计参数,实际工程应用时可以增强算法的适用性。

③ 以控制增量作为系统的输入量,相当于在控制系统中加入了数字积分环节,因此即使模型存在失配问题,也可以得到无静差的控制效果。

3 室内温度控制仿真模型

TRNSYS软件利用TYPE155组件通过COM接口与计算机软件进行通信,并作为一个单独的进程启动,不会影响其他组件的运行和计算。本文主要研究室内温度控制系统,在计算机软件中编制DMC算法控制程序,通过TRNSYS软件仿真建筑物的实际传热过程,在每个仿真时刻向DMC算法控制程序传递用户室内温度,即可通过相应的DMC算法控制程序计算出下一时刻的阀门开度,完成一个控制周期循环。

3.1 建筑模型

以某住宅建筑为例搭建建筑模型,该住宅建筑共3层,每层3个房间,每个房间的长×宽×高均为5.0 m×3.5 m×3.0 m,外窗面积均为2.7 m2。采用Sketch Up软件建立建筑物三维模型(见图1)。每个房间设置为1个单独的热区。为降低户间传热的影响,在内墙和楼板加入保温层。通过围护结构比热容反映其蓄热特性。围护结构主要参数见表1。1层房间从左到右编号分别为f11、f12、f13,2层房间从左到右编号分别为f21、f22、f23,3层房间从左到右编号分别为f31、f32、f33。热负荷主要构成为围护结构传热量、冷风渗透耗热量,并考虑太阳辐射得热量、人员发热量、照明装置及设备发热量。室外气象参数取北方某城市典型年气象数据。

表1 围护结构主要参数

图1 建筑物三维模型

散热器供暖系统为双管下供下回式,每个房间仅1台散热器,额定散热能力为2.8 kW,设计供水温度为60 ℃。用户调节阀设置在每个房间入户回水管上。楼栋单元入口处设置压差控制阀,进行水力解耦,使每个房间的供回水压差维持一定,保证用户调节阀开度与用户供水流量成对应关系,并防止各用户自主调节室内温度产生频繁的振荡。

在TRNSYS模拟中获得预测模型,将所有房间的初始温度设置为20 ℃,先在最小流量下运行48 h,待供暖系统平稳后,在48 h时将所有用户调节阀开度调至最大,按最大流量运行。取第48 h到供暖系统平稳后(第54 h)这段时间温度上升曲线作为动态特性参数的取值范围,即预测模型的建模时域为6 h。考虑到计算时间复杂度和用户调节阀的调节频率,以10 min为采样周期T,则建模时域长度n为36。

3.2 DMC算法参数调优

DMC算法参数主要有预测时域p、控制时域m、误差校正向量h、误差权矩阵Q、控制权矩阵R。这些参数对DMC算法的控制精度、控制稳定性有着重要影响。引入温控误差指标,以用户室内温度偏离设定温度的程度来评价控制效果。温控误差指标越小,说明DMC算法的控制效果越佳。温控误差指标σcomf的计算式为:

式中σcomf——温控误差指标

N——采样数量

y(k)——t=kT时实际室内温度,℃

yset(k)——t=kT时设定室内温度,℃

tN——仿真时间,min

T——采样周期,min,取10 min

以房间f33为例,在供暖中期(1月1—3日),供水温度为60 ℃,采用直线型用户调节阀时,对DMC算法参数的选取进行分析,并作为后续仿真模型的取值。初始室内温度为18 ℃,在0～10 h设定室内温度为22 ℃,在10～24 h设定室内温度为17 ℃。

预测时域p表示对kT时刻以后多少步的输出逼近期望值感兴趣,而误差权系数qi反映了不同时刻逼近的重要性,通常可使误差权系数qi为1,对预测时域p进行选取。设定控制时域m为3、误差校正向量元素hi为1、控制权系数ri为0.01,预测时域p取值范围为6～24。温控误差指标随预测时域p的变化见图2。由图2可知,温控误差指标随预测时域p增大而减小。考虑到计算时间复杂度,预测时域p取18。

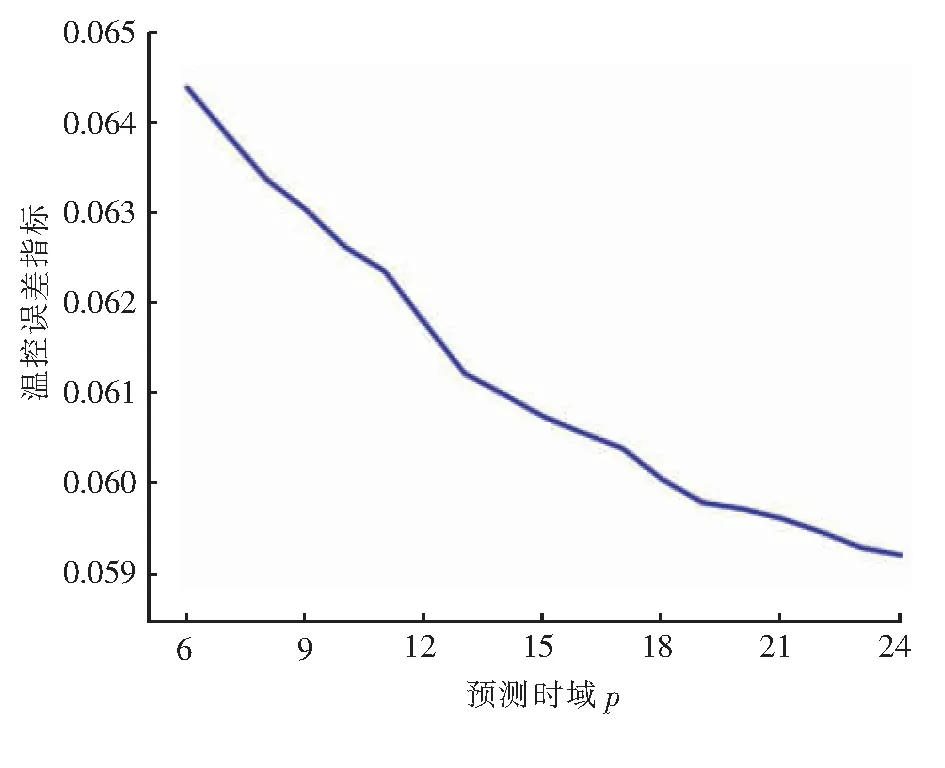
图2 温控误差指标随预测时域p的变化

误差权系数qi仍取1,设定预测时域p为18、误差校正向量元素hi为1、控制权系数ri为0.01,控制时域m取值范围为3～8。温控误差指标随控制时域m的变化见图3。由图3可知,温控误差指标随控制时域m增大而增大。当控制时域m取3时,温控误差指标最小,因此控制时域m取3。

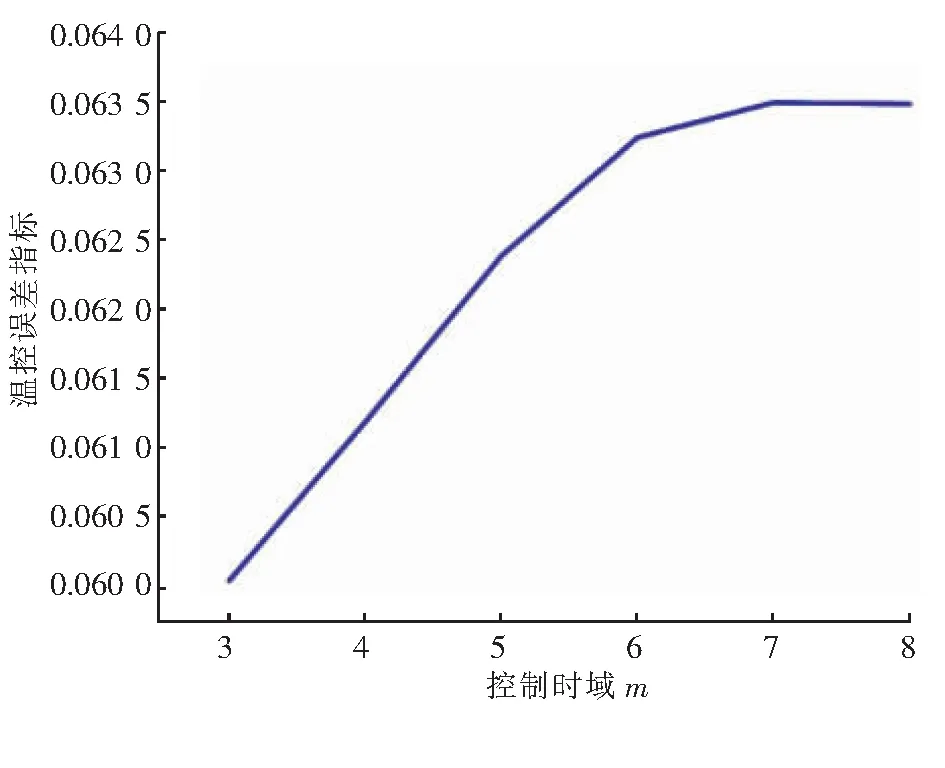
图3 温控误差指标随控制时域m的变化

误差校正向量h中元素hi的选择与其他参数无关,是DMC算法中可以直接调节的参数。它一般在控制系统受到干扰或仿真模型存在失配问题时才会起作用,而对控制的动态响应则没有较大影响。元素hi的选取应兼顾控制系统的鲁棒性和抗干扰性,可取一个关于参数β的方程:

h1=1

hi=βi=2,…,N; 0<β≤1

设定预测时域p为18,控制时域m为3,参数β取值范围为0.5～1.0。温控误差指标随参数β的变化见图4。由图4可知,温控误差指标随参数β增大而减小。当参数β取1时,温控误差指标最小,因此参数β取1。

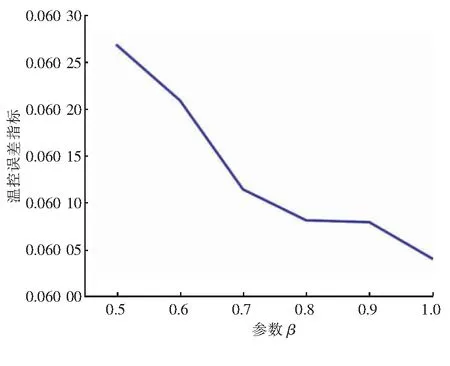
图4 温控误差指标随参数β的变化

控制权矩阵R的作用是适度限制Δum(k)的剧烈变化,并作为软约束添加到优化性能指标中。误差权系数qi仍取1,设定预测时域p为18、控制时域m为3、误差校正向量元素hi为1,控制权系数ri分别取0.01、0.00。控制权系数ri分别取0.01、0.00时,房间f33实际室内温度、用户调节阀相对开度随时间的变化分别见图5、6。由图5、6可知,与控制权系数ri取0.00相比,控制权系数ri取0.01时,实际室内温度偏离设定值的幅度及用户调节阀相对开度变化幅度更小。因此,控制权系数ri取0.01。

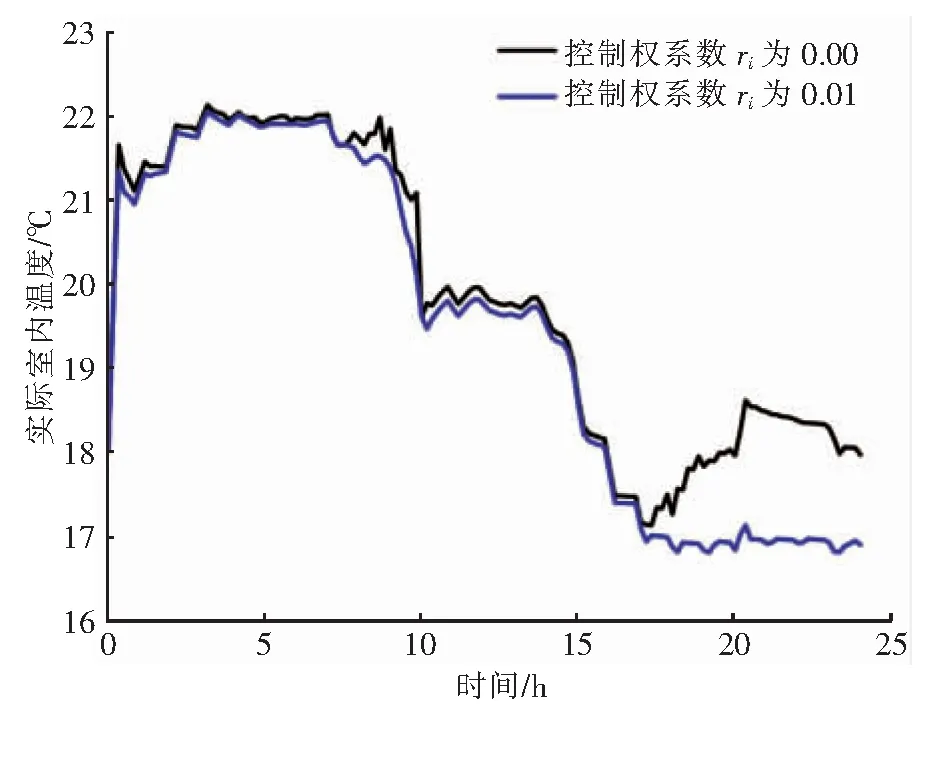
图5 控制权系数ri分别取0.01、0.00时房间f33实际室内温度随时间的变化

图6 控制权系数ri分别取0.01、0.00时房间f33用户调节阀相对开度随时间的变化

4 室内温度控制效果影响因素

4.1 用户调节阀流量特性

以房间f33为例,在供暖中期(1月1—3日),供水温度为60 ℃条件下,分析用户调节阀流量特性对实际室内温度的影响。初始室内温度为18 ℃,在0～10 h设定室内温度为22 ℃,在10～72 h设定室内温度为17 ℃。不同流量特性用户调节阀房间f33实际室内温度随时间的变化见图7。由图7可知,不同流量特性用户调节阀在DMC算法控制下,实际室内温度均接近设定室内温度,这说明DMC算法具有比较强的鲁棒性。

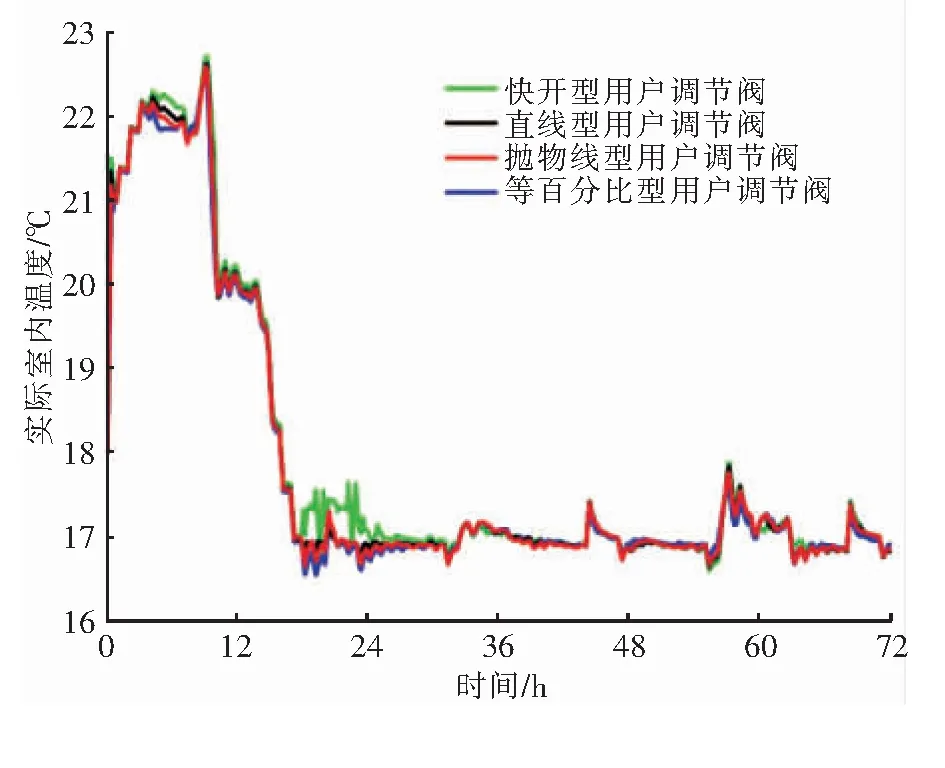
图7 不同流量特性用户调节阀房间f33实际室内温度随时间的变化

仿真时间内不同流量特性用户调节阀房间f33温控误差指标见表2。由表2可知,直线型、抛物线型、等百分比型的温控误差指标接近,因此本文采用比较简单常见的直线型用户调节阀。

表2 仿真时间内不同流量特性用户调节阀房间f33温控误差指标

4.2 供暖时期

以房间f33为例,供水温度为60 ℃,初始室内温度为18 ℃,采用直线型用户调节阀,分析供暖时期对实际室内温度的影响。供暖初期(11月3—5日)、供暖末期(3月21—23日),在0～10 h设定室内温度为23 ℃,在10～72 h设定室内温度为20 ℃。供暖中期(1月1—3日),在0～10 h设定室内温度为22 ℃,在10～72 h设定室内温度为17 ℃。

不同供暖时期房间f33实际室内温度、用户调节阀相对开度随时间的变化分别见图8～10。由图8、10可知,在供暖初期11月4日12:00、供暖末期3月22日12:00,用户调节阀相对开度接近0甚至为0时,实际室内温度均有较大幅度跃升,跃升量分别为2.0、0.7 ℃。在供暖初期11月5日12:00、供暖末期3月23日12:00,实际室内温度平稳,几乎没有跃升。主要原因为:11月4日、3月22日的实际室内温度刚从23 ℃降下来,12:00用户调节阀相对开度已接近0甚至为0,而围护结构的蓄热量未完全释放,且在12:00室外温度和太阳辐射均处于较高水平,因此实际室内温度出现了较大跃升。在与11月4日、3月22日12:00基本一致的室外气象条件下,11月5日、3月23日12:00实际室内温度没有出现明显的跃升,说明此时围护结构蓄热量基本释放,且用户调节阀发挥了调节作用。由图9可知,在供暖中期,室外温度成为影响实际室内温度的主导因素,用户调节阀发挥了调节作用。

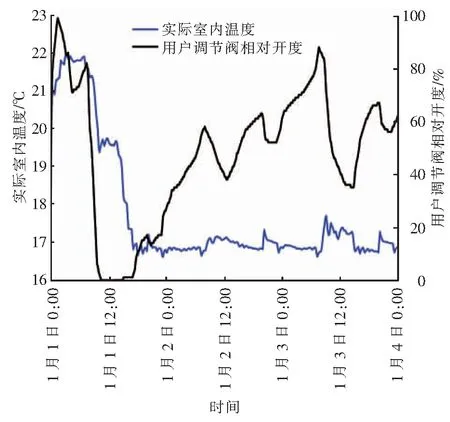
图9 供暖中期房间f33实际室内温度、用户调节阀相对开度随时间的变化

图10 供暖末期房间f33实际室内温度、用户调节阀相对开度随时间的变化

仿真时间内不同供暖时期房间f33温控误差指标见表3。由表3可知,各个供暖时期的温控误差指标相对合理,说明不同的供暖时期,DMC算法均能保持较强的鲁棒性。

表3 仿真时间内不同供暖时期房间f33温控误差指标

4.3 供水温度

以房间f33为例,初始室内温度为18 ℃,供水温度分别取55、60、65 ℃,在供暖中期(1月1—3日)分析供水温度对实际室内温度的影响。在0～10 h设定室内温度为22 ℃,在10～72 h设定室内温度为17 ℃。不同供水温度房间f33实际室内温度随时间的变化分别见图11～13。由图11～13可知,不同供水温度下实际室内温度均能控制在设定值附近,供水温度为55 ℃时实际室内温度波动幅度比较大。

图11 供水温度为55 ℃房间f33实际室内温度随时间的变化

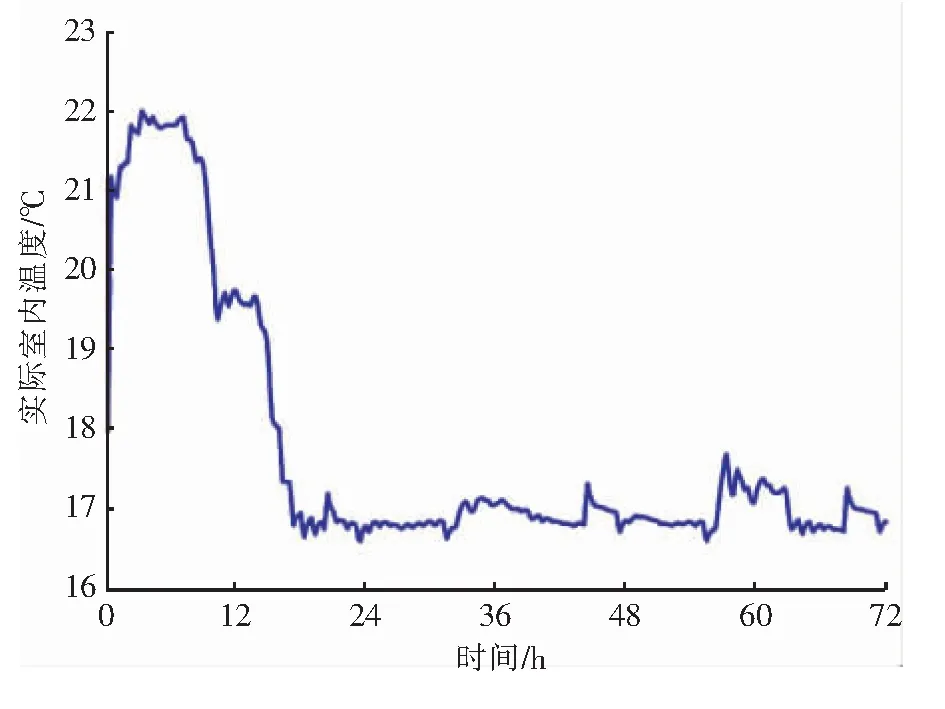
图12 供水温度为60 ℃房间f33实际室内温度随时间的变化

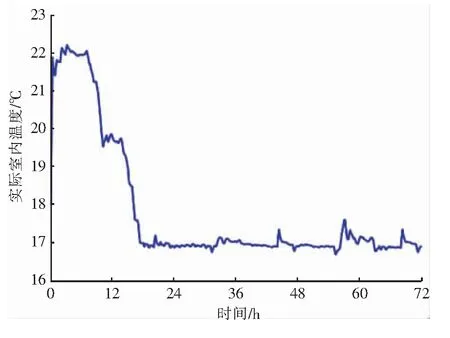
图13 供水温度为65 ℃房间f33实际室内温度随时间的变化

仿真时间内不同供水温度房间f33温控误差指标见表4。由表4可知,不同供水温度的温控误差指标比较接近,供水温度60 ℃的温控误差指标最小。说明DMC算法具有较强的鲁棒性。

表4 仿真时间内不同供水温度房间f33温控误差指标

5 控制效果对比

5.1 预测-反馈预测控制

对于室内供暖系统,输入的边界条件一般可以分成两类:一类是可控输入,如供水流量。另一类是不可控输入,主要包括可以预知但是无法改变的外部作用,如室外温度,以及其他环境、对象等引起的不确定性干扰。预测-反馈预测控制是通过不停调整可控输入来降低不可控输入的影响,从而达到符合期望的控制效果[4]。对于室内供暖系统,室外温度可以通过天气预报提前得知,因此可采用预测-反馈预测控制方式实现室内温度控制。

5.2 比较结果

以房间f33为例,供水温度为60 ℃,室内初始温度为18 ℃,在供暖中期(1月1—3日)比较DMC算法、PID控制、预测-反馈预测控制对室内温度的控制效果。在0～10 h设定室内温度为22 ℃,在10～72 h设定室内温度为17 ℃。

DMC算法、PID控制、预测-反馈预测控制对室内温度的控制效果分别见图14、15。

图14 DMC算法、PID控制对室内温度的控制效果

由图14可知,与PID控制相比,DMC算法对室内温度的控制效果更佳,未出现明显的室内温度超调现象。仿真时间内,DMC算法、PID控制房间f33温控误差指标分别为0.035 303、0.048 001,进一步说明DMC算法对室内温度的控制效果更佳。

由图15可知,DMC算法、预测-反馈预测控制对室内温度的控制效果比较接近。仿真时间内,DMC算法、预测-反馈预测控制房间f33温控误差指标分别为0.035 303、0.035 233,说明预测-反馈预测控制对室内温度的控制效果略优于DMC算法。虽然预测-反馈预测控制利用了室外温度的预测信息,通过前馈补偿提高了控制精度,但与DMC算法相比,实际室内温度曲线并未发生本质变化。因此,预测-反馈预测控制对提升室内温度控制效果有限。

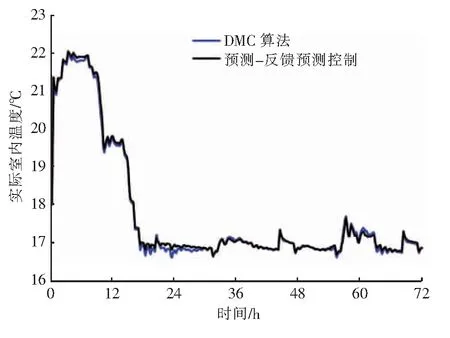
图15 DMC算法、预测-反馈预测控制对室内温度的控制效果

6 结论

① DMC算法具有比较强的鲁棒性。

② 与PID控制相比,DMC算法对室内温度的控制效果更佳。

③ 预测-反馈预测控制对室内温度的控制效果略优于DMC算法,但效果有限。