巧用圆规解决一次函数与折叠问题

姜莹

图形的折叠，实质上就是全等变换，即折叠前后的图形全等. 针对对应点不确定的折叠问题，在抓住折叠形成的等线段和等角，并综合运用图形的性质和勾股定理等相关知识的基础上，若能巧妙地使用圆规，利用半径相等，则可以快速锁定对应点的位置.

例题精析

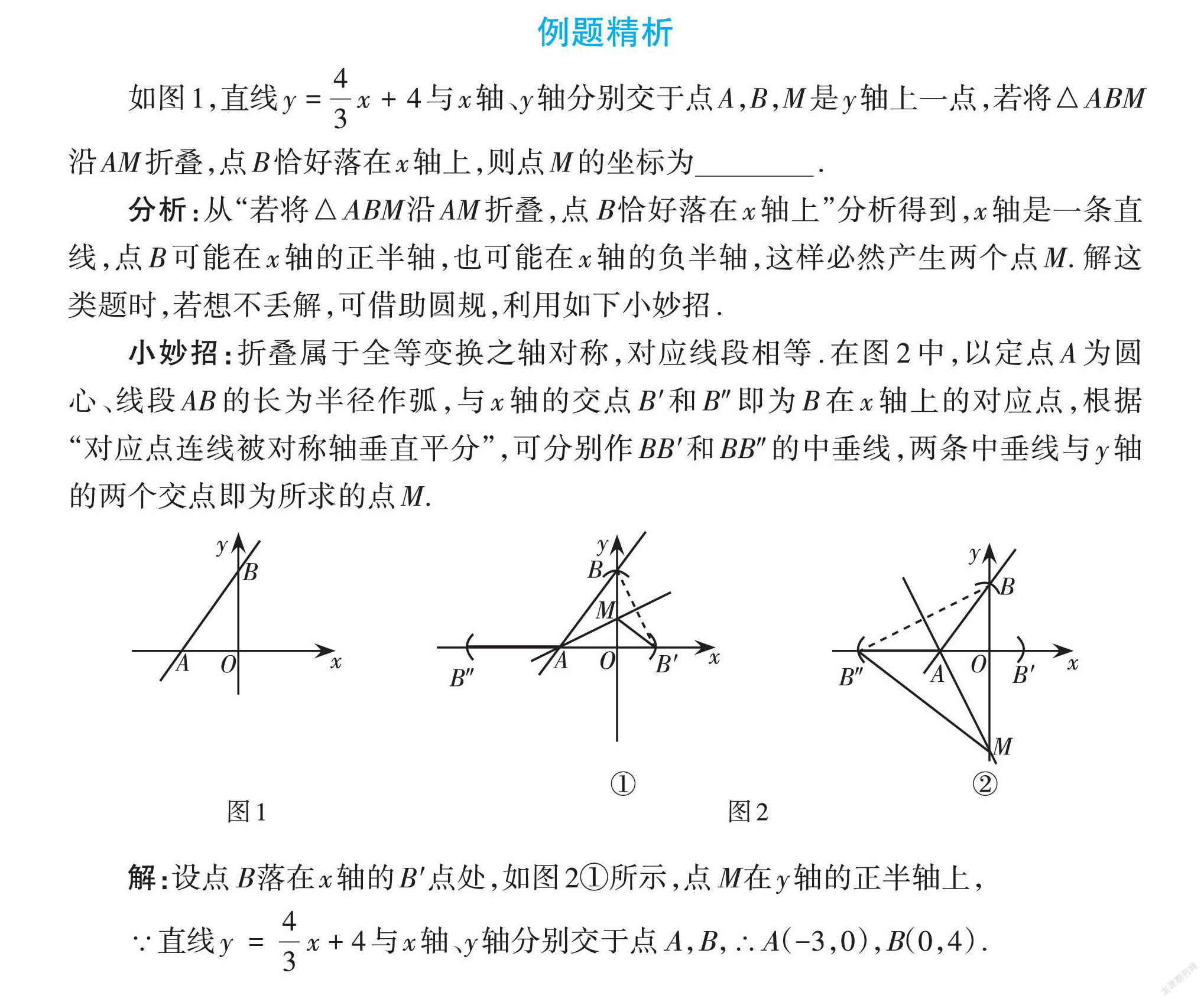
如图1，直线[y=43x+4]与[x]轴、[y]轴分别交于点[A]，[B]，[M]是[y]轴上一点，若将△ABM沿[AM]折叠，点[B]恰好落在[x]轴上，则点[M]的坐标为 ．

分析：从“若将△ABM沿[AM]折叠，点B恰好落在[x]轴上”分析得到，[x]轴是一条直线，点[B]可能在[x]轴的正半轴，也可能在[x]轴的负半轴，这样必然产生两个点[M]. 解这类题时，若想不丢解，可借助圆规，利用如下小妙招.

小妙招：折叠属于全等变换之轴对称，对应线段相等.在图2中，以定点[A]为圆心、线段[AB]的长为半径作弧，与x轴的交点B'和B[″]即为[B]在[x]轴上的对应点，根据“对应点连线被对称轴垂直平分”，可分别作BB'和[BB][″]的中垂线，两条中垂线与y轴的两个交点即为所求的点[M].

解：设点B落在x轴的B'点处，如图2①所示，点M在y轴的正半轴上，

∵直线y  =  [43] x + 4与x轴、y轴分别交于点A，B，∴A（-3，0），B（0，4）．

∵将△ABM沿AM折叠，∴[AB'=AB]．

∵OA = 3，OB = 4，∴[AB=5=AB']，∴[B'O=AB'-OA=2]．

设点M的坐标为（0，m），则[B'M=BM=4-m]，

[在Rt△B'OM中，∠MOB'=90°]，由勾股定理，得 [B'M2=B'O2+OM2]，

∴m = [32]，即M [0，32]，

如图2②所示，点M在y轴的负半轴上，设点M的坐标为（0，n），

由折叠知，AB[″] = AB = 5，B[″]M = BM， ∴B[″]O = 8，B[″]M = 4 - n．

[在Rt△B″OM中，∠MOB″=90°]，根据勾股定理可得[B″M2=B″O2+OM2]，

∴[4-n2=82+-n2]，∴n = - 6，即M（0，-6）．

综上所述，点M的坐标为[0，32]或（0，-6）．

巩固训练

如图3，直线[y=-125x+12]与x轴、y轴分别交于点A，B，M是y轴上一点，若将△ABM沿AM折疊，点B恰好落在x轴上，则点M的坐标为 ．（答案见本页）

方法迁移

如图4，点E为长方形ABCD的边AB的中点，连接CE，作射线DE，若点F为长方形ABCD边上任意一点，沿EF将矩形折叠，使点A恰好落在射线DE上，已知AD = 2，CD = 4，则DF = ．（答案见本页）

（作者单位：辽宁省实验中学分校）