饱和交通流状态下公共交通优先感应控制优化
2023-05-12吕悦晶同奕萌张萌萌薛永康谢文俊
吕悦晶 同奕萌 张萌萌 薛永康 谢文俊
(武汉科技大学汽车与交通工程学院1) 武汉 430065) (青海省公路局2) 西宁 810001) (山东交通学院交通与物流工程学院3) 济南 250357)
0 引 言
公共交通具有载客量大、人均占用道路资源小、运行效率高等优点,优先发展城市公共交通成为解决城市交通拥堵的一条重要途径.
随着“公交优先”研究的深入,公交优先控制策略逐步被分为三类:被动式优先、主动式优先和实时优先.早期对公交优先的研究以被动优先与主动优先为主.被动优先是通过收集公交车辆运行的历史数据来预测需要的优先等级,因此无法适应实时交通需求的变化.Sunkari等[1]结合美国《公路通行能力手册》(HCM)中的信号交叉口延误计算公式,基于两类周期加权延误建立了公交信号优先配时优化模型.马万经等[2]提出了一种考虑时空资源组合优化的被动优先模型,实验证明在对社会车流影响较小时,可以显著降低公交车辆的车均延误.主动式优先是依靠检测器对公交车辆运行情况进行识别分析,实时调整交叉口信号控制方案,从而实现公交车辆的优先通行.Vincen等[3]提出了延长绿灯时间和缩短红灯时间两个基础性无条件公交优先策略,但因为主动优先不能协调公交车辆与社会车辆的运行效益,会对其他非优先交通流正常通行产生很大干扰的弊端[4].至20世纪90年代中期逐步被实时优先所替代,实时优先控制以Chang等[5]的研究为开端.高先觉[6]在传统公交优先感应控制的基础上,根据各车的到达情况实时对非优先相位绿灯进行压缩,确保公交优先.
5G、物联网技术、云计算等新一代信息技术的发展,改变了传统交通信息采集和交通控制方法.在车路协同环境下,公交车辆可通过车载设备与路侧进行通信,可以获得更精确的车辆运行实时位置、加减速、运行轨迹等信息,为公交优先控制的研究提供了新的技术支持.魏然[7]提出了在一种在车路协同环境下综合考虑乘客人均延误减少的公交优先信号控制方法,运用蜻蜓优化算法求解延误模型,并使用VISSIM进行仿真分析,证明了此公交优先方法的有效性.罗浩顺等[8]结合公交车以车队形式通过交叉口的需求,提出了一种以交叉口综合延误为目标,通过发射预指令车速信息,结合车速引导措施的公交优先信号控制方法,使公交车顺利通过交叉口,减少车队截尾.
公交优先控制策略研究在提高公交运行效率、缓解交通拥堵等方面已经取得了很多成果[9].但在饱和交通状态下,非优先车流的到达率远大于驶离率,交叉口内部的非优先相位车辆排队长度不断增加,甚至导致多次排队现象发生,交叉口的整体运行情况受到了干扰.本文基于此,为使得交叉口整体效益最优,提出一种饱和交通流状态下的公交优先感应信号控制模型.并以实际交叉口为例进行仿真验证.
1 公交优先控制策略研究
1.1 前提假设
①交叉口进口道设有公交专用道;②交叉口信号控制设有公交专用相位;③交叉口内部车辆都装有车载设备OBU,可与路侧设备RSU进行通信;路侧设备RSU可以接收车辆的当前车辆位置信息、行驶速度及实时路况信息等;④路侧设备RSU通过与车辆的车载设备OBU信息交互后,可通过内置的TSP算法预测出车辆抵达当前交叉口停车线的时间;⑤不考虑车道宽度、坡度等要素对行车速度的影响,忽略非机动车及行人对交叉口运行的影响;⑥公交车匀速行驶,只有进站和出站时做减(加)速度一定的匀减(加)速运动.
1.2 非优先相位的最小绿灯时间模型
将路侧设备RSU设置在路口,采集非优先相位的实时车流信息.根据交叉口非优先相位的绿灯时间确定排队溢出点的位置,即通过车载设备与路侧设备进行通讯,采集非优先相位的绿灯时间内所能通过的车辆数以确定出排队溢出点位置.溢出点前排队的车辆可以在下一个绿灯时间内通过交叉口,在溢出点后到达的车辆在下一个绿灯时间内无法正常通过交叉口,需再等待一个绿灯时间才能通过交叉口.
结合公交优先策略,为了减少非优先相位车辆在交叉口的排队,提出非优先相位的最小绿灯时间模型.
(1)
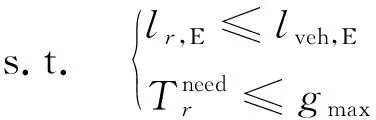
(2)
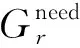
1.3 公交优先感应控制优化模型
基于非优先相位的最小绿灯模型,提出一种适应饱和车流状态下的交叉口公交优先感应控制信号模型,其控制策略见图1.
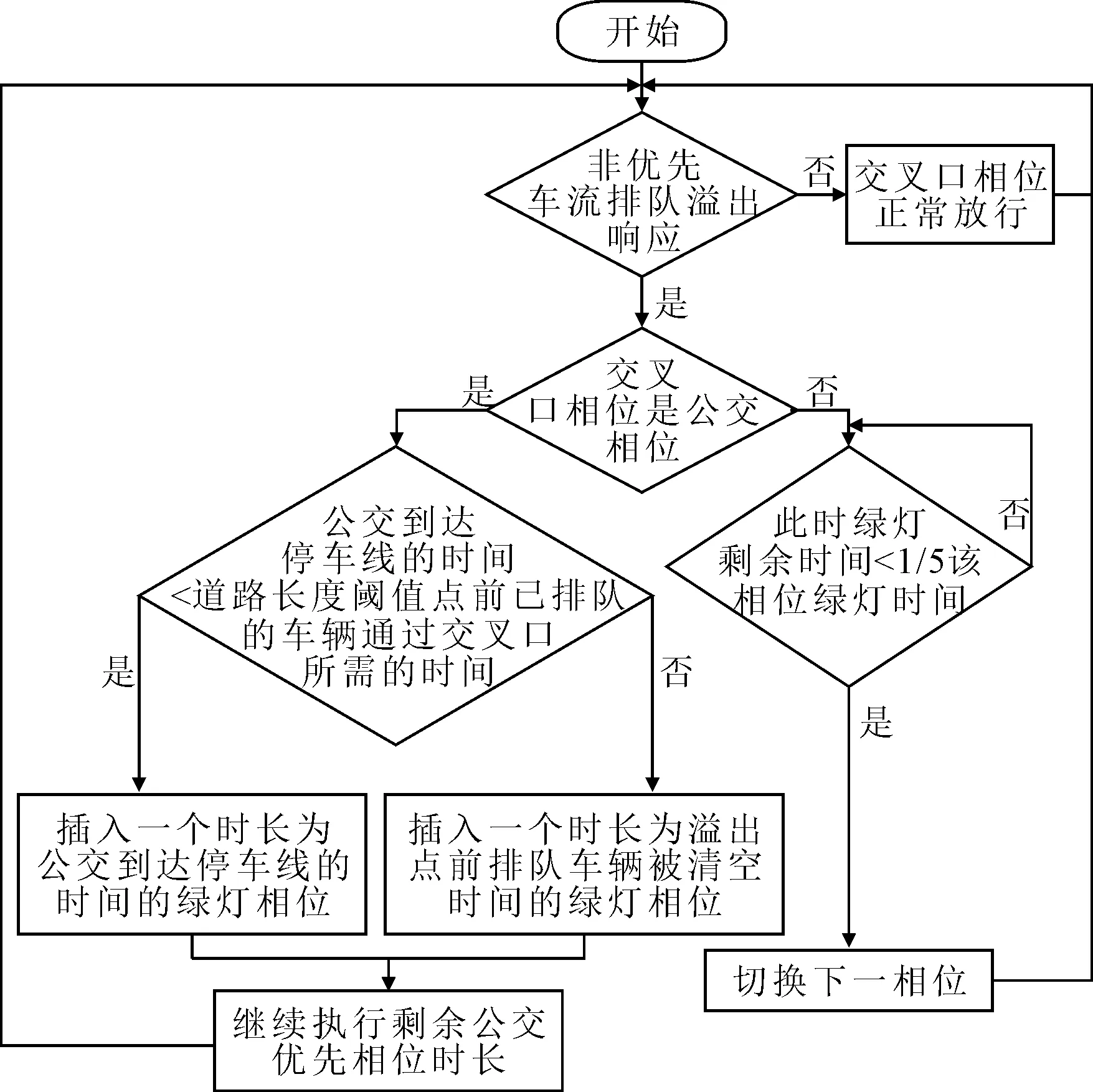
图1 感应控制策略
1.4 控制参数
1.4.1非优先相位排队消散约束
根据饱和交叉口非优先相位车辆的交通特性,建立交叉口非优先相位最大排队长度约束,非优先相位的排队车辆为
(3)
饱和车流状态下,交叉口非优先相位绿灯时间允许的最大排队长度不能超过溢出点的位置,即:
(4)
因此,非优先相位车辆的消散时间为
(5)
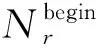
1.4.2公交车辆到达交叉口停车线的时间
1) 公交车辆在站台上游 此时的公交车辆位于站台上游,见图2.公交车辆需要经过减速进入公交站台、在站台完成乘客上下车交换和加速驶出公交站台三个过程,才可达交叉口停车线.
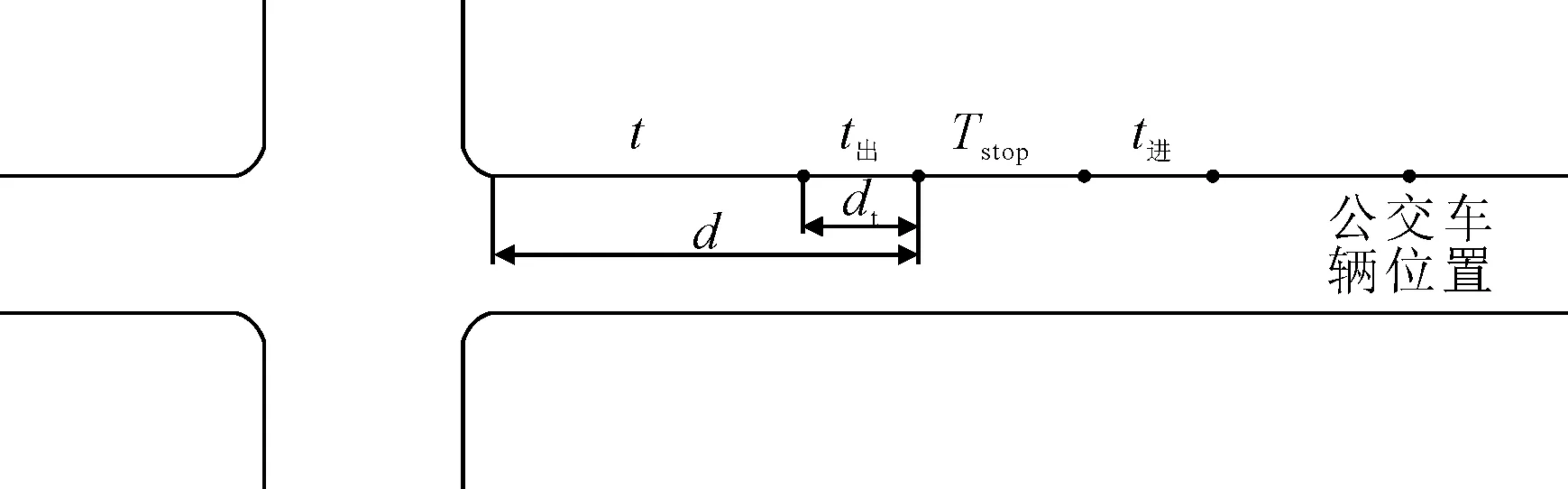
图2 公交车辆位于站台上游
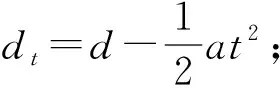
当溢出点检测到非优先相位车辆溢出后,此时公交车辆还需
(6)
式中:a为公交行驶加(减)速度,m/s2;Tstop为公交车辆的停站时间,s;t进、t进分别为公交车辆进出站时间,s;Vcur为公交车辆在公交专用道上正常行驶的速度,m/s;d为公交站台距交叉口停车线的距离,m.
2) 公交车辆在站台内 溢出点检测到非优先相位溢出时,若此时的公交车辆位于站台内,公交车辆到交叉口停车线只需要经过加速驶出站台,再保持当前车速行驶至停车线两个过程,见图3.因此在这种状态下公交车辆到交叉口停车线所需要的时间与公交车辆在站台上游的计算方法类似,即:
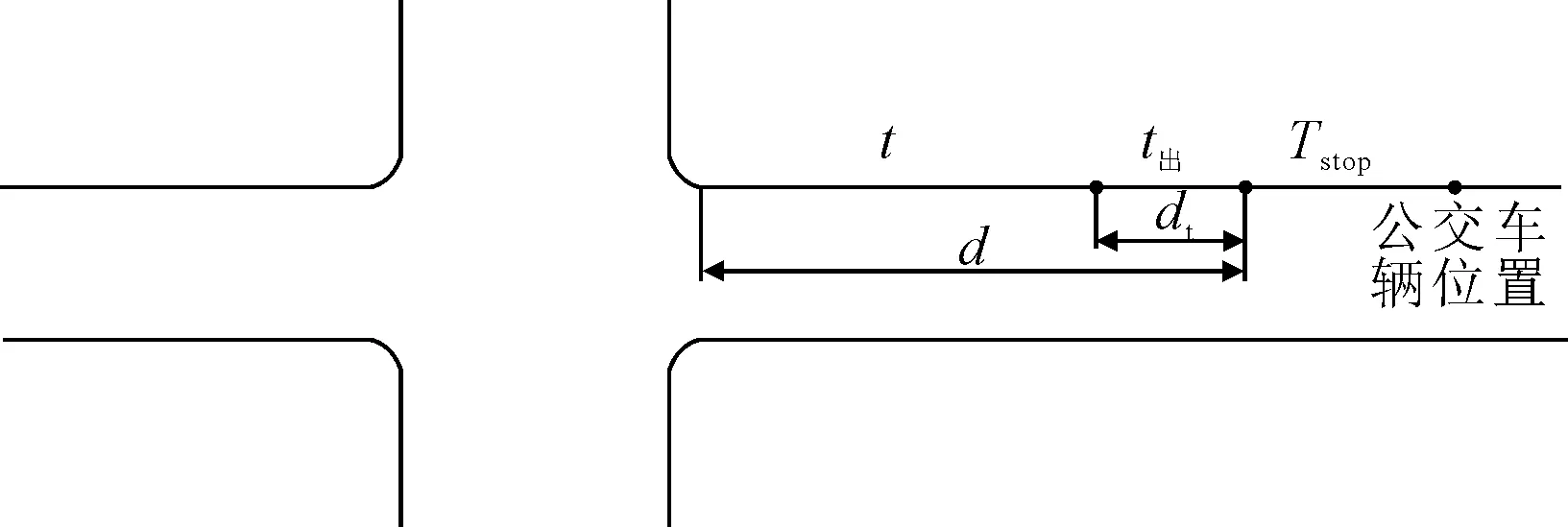
图3 公交车辆位于站台内
(7)
3) 公交车辆在站台下游 溢出点检测到非优先相位车辆溢出时,若此时公交车辆位于站台下游,则此时公交车辆只需保持当前行驶速度继续行驶至交叉口停车线即可,见图4.因此,公交车辆行驶至交叉口停车线的时间为
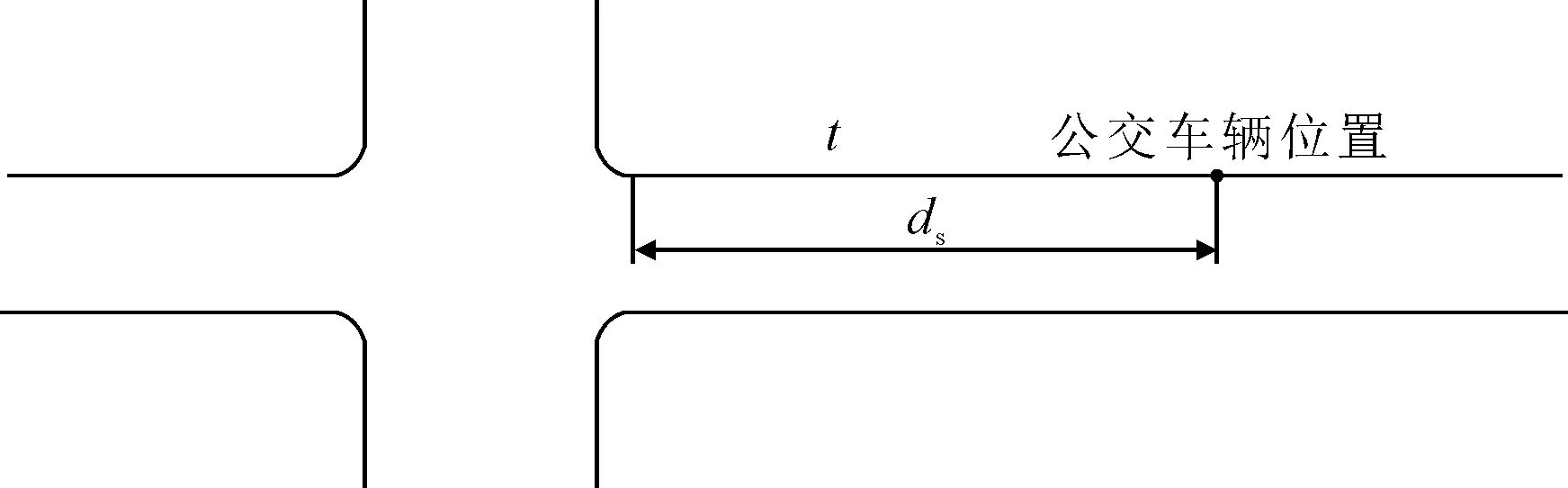
图4 公交车辆位于站台下游
(8)
式中:ds为公交车辆距交叉口停车线的距离,m.
1.4.3感应信号控制约束
感应信号控制的基本原理是在最短绿灯结束前,若检测到车辆仍有通行的需求,则继续延长一个单位绿灯时间,绿灯时间一直可延长至交叉口最大绿灯时间.即在预置的时间间隔内,绿灯可延长,反之中断.本文所提出的信号控制属于感应信号控制,所以约束条件为
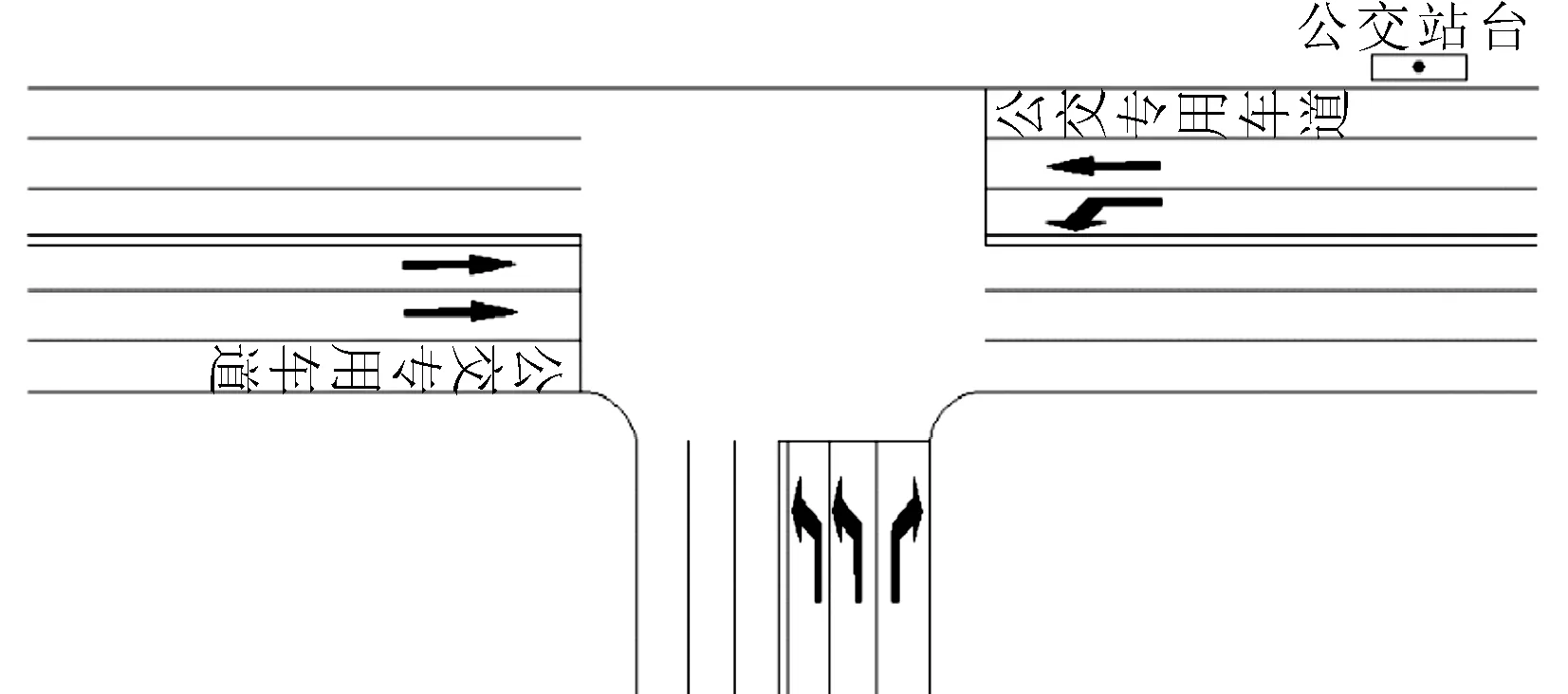
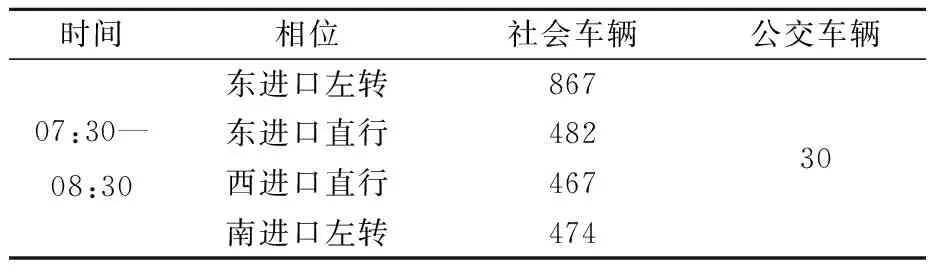
gmin (9) 式中:gei为非优先相位有效绿灯时间;gmin为最小绿灯时间;gmax为最大绿灯时间,绿灯延长时间不超过周期总时长的10%. 有效绿灯时间是指交叉口实际显示的绿灯时间减去该相位总损失时间后实际用于该相位的车辆通行的时间,即一个周期的有效绿灯时间为周期时长减去周期内总损失时间. (10) 式中:L为绿灯损失时间. 信号交叉口延误是反映车辆在交叉口上受阻、行驶时间损失的评价指标.对于设置有公交专用道的交叉口,公交车辆与其他社会车辆分道行驶,两种不同类型的车辆的到达率与饱和流率都不相同,在交叉口产生的车辆延误也不相同. 考虑公交车和非优先相位车辆的车辆载客数、运行特性差异,以交叉口人均延误最小为优化目标,采用交叉口延误模型对交叉口进行评价,即: (11) 以济南市某一T型交叉口实际调研数据为例,此交叉口的社会车辆拥堵严重,公交相位为东西直行相位,交叉口车辆右转不受信号控制.交叉口基本设置见图5,其中东西向为通行主干道并设有公交优先相位,进口道由内向外分别为左转车道、直行车道、公交专用车道. 图5 交叉口基本概况 选取调查时段为早高峰(07:30—08:30),选用此交叉口进行仿真实验,将东进口方向的左转车流作为感应控制车流,该交叉口的车流到达情况见表1. 表1 交叉口各车道交通量 单位:pcu/h 根据实际调查,此交叉口为三相位信号控制,周期为130 s,其相位相序以及信号配时参数,见表2. 表2 信号配时方案 单位:s 为了方便计算,给定以下条件及参数值. 1) 交叉口的相位相序设计以及相位间隔时间保持不变. 2) 根据调查,社会车辆平均载客量1.5人/辆,公交车辆平均载客量为25人/辆. 3) 根据实际调查,一个绿灯时间内平均可正常通行社会车辆15辆,因此方案中溢出点设置在距交叉口停车线100 m处. 2.2.1社会车辆元胞自动机模型运动规则 对于社会车辆i而言,在t时刻它的位置为Xi(t),速度为Vi(t),车长均为lc,在停车线上游设置长为ld的减速区,其运动规则如下. 1) 加速规则 Vi=min(Vi(t)+a+,Vmax) (12) 式中:a+为车辆的加速度值. 2) 出于安全考虑对于车速的限制,在本模型中相邻两辆车的最小间距为1. Vi=min(Vi,di(t)) (13) 式中:di(t)为车辆i与前车的间距, di(t)=Xi+1(t)-Xi(t)-lc-1 (14) 3) 减速规则 对于在绿灯周期的车辆或在红灯周期但不在减速区内的车辆i,考虑司机驾驶行为中的不确定因素而导致的随机减速: Vi=max(Vi(t)-a-,0) (15) (16) 式中:pd为随机减速概率;a-为随机减速度;r为在[0,1]之间均匀分布的随机数. 对于在红灯周期并处于减速区内的车辆i: (17) Vi=max(Vi(t)-a-,0) (18) Δi=Xs-Xi(t) (19) 4) 位置更新规则 车辆运动采用并行更新方式,车道采用周期性边界条件. Xi(t+1)=Xi(t)+Vi(t) (19) 2.2.2公交车辆元胞自动机运行规则 对于公交车辆而言,公交停靠站为直线式停靠站.公交停靠时间TS,公交停靠区长度Lpark进入公交站台前有一段长LD的减速区. 1) 加速规则 Vj=min(Vj(t)+a+,Vmax) (20) 2) 减速规则 未在减速区的公交,依据恒速控制模型进行减速 Vj(t+1)=max(Vj(t+1)-a-,0) (21) (22) 在减速区的公交 (23) Vi=max(Vi(t)-a-,0) (24) Δj=XT-Xj(t) (25) 3) 位置更新规则 Xj(t+1)=Xj(t)+Vj(t) (26) 选取交叉口车均延误、人均延误和交叉口平均排队长度对交叉口运行状况进行评价,得到设计方案的评价结果见表3~4. 表3 各车道车均延误 单位:s 表4 人均延误和平均排队长度 2.3.1交叉口车均延误 与对照方案相比,优化方案中,作为感应控制车流的东进口左转车流车均延误减少了31.9 s,车均延误减少了42.53%.其余车流的车均延误虽有增加,但对交叉口的通行影响较小.说明优化方案中提出的感应信号控制模型在饱和交通流状态下,可以有效地减少社会车辆的延误. 2.3.2交叉口人均延误 与对照方案相比,优化方案中的交叉口人均延误减少了7.55 s,人均延误减少了15.64%.说明优化方案中提出的感应信号控制模型在饱和交通流状态下,可以减少交叉口的人均延误. 2.3.3交叉口平均排队长度 在交叉口运行时,每10 s记录一次在交叉口停车排队的车辆数.通过对单位时间内交叉口停车排队的车辆数进行统计.与对照方案相比,优化方案中的平均排队长度减少了5.977辆,下降了45.88%. 文中基于交叉口已经实施公交优先的策略下,提出了一种新的感应信号控制方法.以交叉口综合通行效益最大化为目标,统筹考虑了交叉口的通行效益,既保证了公交车辆的优先通行,又减少了非优先相位车辆在饱和车流状态下的排队.通过使用本文搭建的python元胞自动机仿真平台,验证了本文提出的控制方法可以保证在公交车辆的顺畅通行下,缓解了社会车辆排队通过交叉口的情况,提高了交叉口的通行效率. 实际中,行人和非机动车对交叉口车辆的正常通行会造成一定的干扰,今后需对交叉口的各种交通流进行综合考虑,并针对交叉口的多股车流的公交优先信号控制方法进行深入探讨.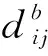
2 实例分析
2.1 仿真方案设计

2.2 仿真平台搭建
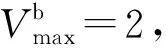
2.3 仿真方案结果评价分析


3 结 束 语
