公交一票制乘客精细化分类研究

李 军,区静怡,赵文婷

(中山大学 智能工程学院,广东 广州 510006)

0 引 言

随着移动互联网时代的多样化发展,公交出行给乘客带来了许多便利。大部分采取公交一票制的城市公交的付费方式不再拘泥于现金,而衍生出刷卡、NFC以及二维码支付等多元化的支付方式。虽然支付方式不同,公交一票制下乘客在乘坐公交工具时仍只需要进行一次付费行为。公交一票制乘车体系仅记录乘客的上车时间和站点信息,对乘车距离有差异的乘客均采用统一的收费原则。由于该体系缺乏乘客下车时空信息,难以体现不同乘客的完整出行特征,因而给公交一票制下的乘客分类带来了挑战。

目前乘客群体分类研究主要分为主观分类和客观分类2种基础类型。不同的乘客伴随着不同的社会经济属性,在主观分类中,乘客的个人特征、家庭特征以及出行目的等均可作为分类的重要依据[1-3]通过构建特征矩阵得到体现。乘客信息一般可通过问卷调查获得,但调查群体量大,且存在主观性强的缺陷。同时,根据乘客刷卡的卡片类型,如学生卡、老年卡和普通卡等,存在预设乘客身份和行为特征的情况,易影响乘客分类客观性。因此客观分类可避免过强的主观性分类,通过客观因素建立乘客分类模型,如出行强度、时间规律性、空间规律性等。针对出行强度和时间规律性,采用工作日高峰时段出行频率和时段等特征判断乘客活动频率与性质[4-5]。判断乘客的空间规律性时,一般采用出行距离或任2个站点的地理相近性进行体现,研究认为后者可取1 000 m以内的值作为判断值[6-7]。在选择聚类方法上,有研究从时间划分的角度使用K-means算法将乘客聚类成3类,在结合时间和空间的规律性上,可进行组合划分,但类别数较少[8],或通过DBSCAN聚类算法[9]与数据挖掘结合对乘客的出行行为进行分类;此外也有研究使用Two-Step聚类算法[10]并将乘客分成5种类型;通过细化出行强度的定义和优化初始聚类中心,有研究使用混合类型的聚类算法[11]将乘客分为4类;其中,各聚类算法各有优劣,K-means算法是一种迭代求解的聚类分析算法,给定预定的分类数,逐步迭代直至最优,可使类别内的平方误差最小,而类别间差距明显。DBSCAN聚类算法优点在于不需要定义聚类个数,可识别任意形状的聚类,对于密度差距较大的簇则难以处理[12];Two-Step聚类算法包括预聚类和聚类,其优点在于能同时处理分类变量和连续变量,使用更为客观的BIC准则[13],自动选择最佳簇数量。虽然上述聚类方法能在没有先验知识的情况下对研究对象进行分类,但仍存在单次聚类效果笼统的问题[11]。

上述以客观因素分类的研究中,对乘客的空间规律性分析均建立在可获取乘客上下车信息的情况,对于采用公交一票制的乘客分类适用性较低,且既有分类较为笼统,难以准确表示每一类别乘客的特征。已有研究可通过推断下车站点的方式对下车信息进行补全,如出行链匹配法或站点吸引权法[14-16],但推断方法对数据要求较高,乘客分类结果准确率受站点推断结果的影响。综上所述,针对公交运营所采用的一票制付费情况,笔者从乘客的上车时空信息考虑,推导其乘车强度、时间特性、空间特性及高峰特性,提出一种可应用于公交一票制分类方法,使用组合聚类的方法构建一个全群体乘客的精细化分类模型,采用广州市公交乘客的刷卡数据对模型作实例分析,并验证该分类模型的稳定性和有效性。公交乘客精细化分类模型可为公交服务运营优化、个性化公交服务和公交需求预测等带来新的契机。

1 乘客分类模型构造

1.1 分类指标构建

考虑相关性、误差以及公交一票制所记录的上车信息数据,选取乘客在乘车强度、时间特性、空间特性以及高峰特性的表现对公交一票制乘客分类模型进行分析。

1.1.1 乘车强度

乘车强度反应了乘客对某种交通方式的依赖性,根据公交一票制出行特点,分别以日和周为单位,乘客k的乘车强度表征项由以下4个指标构成:① 日均乘车次数sk为乘客对公共交通的依赖程度;② 乘车周数wk为以周为单位周期性出行强度;③ 每周平均乘车天数Ak为乘客单位周期内的公交利用程度;④ 周乘车天数标准差ηk为指标Ak的稳定程度。

1.1.2 时间特性

由于公交一票制只有上车信息,因此围绕上车时间来构建这一指标。针对现实中存在大量的单日单次乘车用户的特点,笔者把全体乘客都具备的首次乘车行为作为重点的时间特性指标,而周期性的指标围绕工作日和非工作日进行构建。乘客k的时间特性由以下指标进行刻画:① 日均首次乘车时间Tk为乘客在统计周期内的首次乘车时间平均值;② 日首次乘车时间标准差σk为乘客首次乘车时间Tk的波动程度;③ 周工作日平均乘车天数Rk为乘客工作日的周期性公交利用程度;④ 周非工作日平均乘车天数Nk为乘客非工作日的周期性公交利用程度。

1.1.3 空间特性

公交站点是体现乘客乘坐公交的空间规律的重要指标,有研究表明乘客的首次和末次乘车站点有很大可能为居住地和活动目的地,且互为起点和终点[17-18]。考虑到一票制下的乘车行为无下车信息记录,选取乘车日的首次乘车和末次乘车来揭示乘客蕴藏的乘车空间特性。此外由于乘客对公交线路的选择不是唯一的,在出行端点区域内公交站点都有可能被选择,乘客在出行端点邻近区域的集中程度可以作为一项有效的分类指标,该指标值越高,表明其空间规律性越高。

我国对常规公交和轨道交通的站点服务区域分别是以500 m和800 m为半径计算时,覆盖率不得低于90%,因此可以设定相邻站点之间距离ε是否小于500～1 000 m来判断任意两个站点是否可认为是乘客在乘车时可同时考虑的邻近站点。假设乘客k在总研究周期范围内的总乘车天数Dk大于1 d,分别计算其日首次和末次乘车站点邻近指数。

(1)

(2)

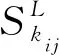
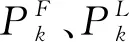
1.1.4 高峰特性

工作日的公交出行人群存在大量通勤者,有着明显的早晚高峰特征,而在非工作日内则较不明显。乘客在工作日早晚高峰时段的乘车站点邻近指数,可对乘客的通勤特征进行刻画,乘客在所给定的高峰时段中乘车站点规律性越强,则其指标取值更高。在统计时段内有多次乘车行为的乘客k,分别计算早晚高峰指标公式如下。

(3)

(4)

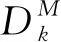
分类模型中所用到的各特性下各特征指标的单位、类型以及取值范围如表1。由于存在部分乘客在空间特性和高峰特性指标计算时需分类取值,因此对该部分乘客进行额外标定以作区分,故此类指标为组合型。

表1 公交一票制乘客分类指标

1.1.5 指标筛选

确定分类模型下的指标构建后,针对具体研究对象,部分指标可能存在较强的相关性,影响分类结果。笔者选择斯皮尔曼相关性系数对指标进行计算筛选,其指标取值范围为[-1,1]。在筛选过程中,对于相关性系数落在[-0.5,0.5]中的指标可认为相关性较弱,对于落在此区间外的指标对可认为相关性较高,应考虑予以剔除。

1.2 乘客分类

公交一票制下的乘客信息中蕴藏其分类特征,由于乘客类型多样,随机性强,一次分类难以精细化描述乘客特征,笔者采用多次分类的方法。

考虑到所选取的特征指标多样,K-means聚类适用于数值型的变量,Two-Step聚类分析法适用于分类型和数值型的变量。其中Two-Step聚类的第1阶段是预聚类,采用BIRCH算法中CF树生长的思想,依次遍历数据点,生成CF树,同时预先聚集密集区域内的数据点形成小的子簇。第2阶段则是聚类阶段,以子簇为对象,利用凝聚法逐个合并距离最近的簇,直至达到期望的数量。期望的最佳簇数通常采用施瓦兹贝叶斯准则(BIC)进行初估,确定大致范围;其次根据前后两个最近簇距离的比值,精确定位最佳簇数。

首先,对乘客进行一次分类。由于乘客分类指标中除了连续型指标,还存在组合型指标,因此在Two-Step聚类时将此类指标视作分类型,得到若干个簇。在此次分类中并未体现乘客在组合型指标的表现,而其设立旨在对在此类指标下有表现的乘客予以描述。因此将首次聚类下的簇进行划分,将组合型指标中空间特性分类和高峰特性均表现一致的簇称为清晰簇{C1,…,Cx},反之则为非清晰簇{U1,…,Uy}。

其次,对乘客进行2次分类。为实现乘客的精细化分类,需对清晰簇和非清晰簇进行再次聚类。对清晰簇中每一个簇分别进行K-means聚类,对每一个簇均定义一个聚类特征组,且组合型指标的取值还原为[0,1],作为连续型指标分析。在聚类过程中,设置适当的聚类K值。如对簇C1进行聚类,选取聚类值K1,得到聚类结果{C1-1,…,C1-K1}。对所得到的非清晰簇视作一个簇,根据簇的特点调整相应的特征组,若此类簇仍存在分类型指标,则需进行再次Two-Step聚类。通过上述方法,可构建一个全群体乘客的精细化分类模型。聚类过程如图1。

图1 组合聚类下的公交一票制乘客分类流程

2 实例分析

选取广州市公交一票制IC卡数据对本方法进行验证,数据采集时间为2014年3月—2014年6月。

为排除乘车周期性的影响,选取每月其中一个自然周的刷卡记录作为研究数据。乘客刷卡数据包括刷卡信息、乘客卡号、刷卡时间、线路编号及刷卡站点,公交运营和设施数据包括线路站点表及站点空间信息。

在分类指标计算中所需的乘客信息为卡号、刷卡时间、站点及其经纬度。所得用户数为2 580 576名,所有刷卡记录为51 558 503条。

2.1 指标筛选

站距判断阈值ε设为1 000 m,为了拓宽早高峰和晚高峰时段,分别取06:00—10:00和17:00—21:00。采用斯皮尔曼相关性系数对各分类特征进行相关性分析,两两特征间的相关性系数如图2。

图2 两两特征间的斯皮尔曼相关性系数

由于存在多个特征指标冗余的情况,因此需要剔除乘车周数和每周平均乘车天数2个指标,剩余指标数用于聚类分析。

剔除重复指标后对乘客进行乘车统计,初步情况表明,4周内仅一次乘车的乘客占15.01%,无空间特性表现;约50%的用户在高峰特征中的统计时段内仅有一次或无乘车行为。

2.2 聚类结果

首先,进行一次分类,采用Two-Step聚类法,将乘车强度和时间特性的特征作为连续型变量,将空间特性和高峰特性的特征作为分类型变量并加入目标变量选择器中,选定对数似然距离进行测量,设置施瓦兹贝叶斯准则(BIC)作为聚类准则,得到的最优聚类数为5簇,聚类效果良好。对所得到的簇根据空间特性和高峰特性的表现进行划分,其中簇1和簇5为清晰簇,簇2、簇3、簇4为非清晰簇。

其次,进行2次分类,按照簇顺序依次进行精细化分类:对簇1进行K-means聚类,观察簇特征后取对应聚类特征组,迭代45次后收敛,并分为4个类别,记作类别1～类别4。同时,将簇2～簇4视作原始数据并再次进行Two-Step聚类,选择相应的连续型和分类型特征组,共得到3个类别,记作类别5～类别7。对簇5同样进行K-means聚类,由于簇5在空间特性和高峰特性的分类型指标上无表现,因此取乘车强度和时间特性指标作为聚类特征组,10次迭代后实现收敛,并分为2个类别,记作类别8、类别9。综上,本案例的乘客精细化分类可分为9个类别。根据各类别乘客的特征,表2分别给出了各类别乘客定义。结合组合聚类的分类结果,各类别乘客的数量及所占的比例如图3。

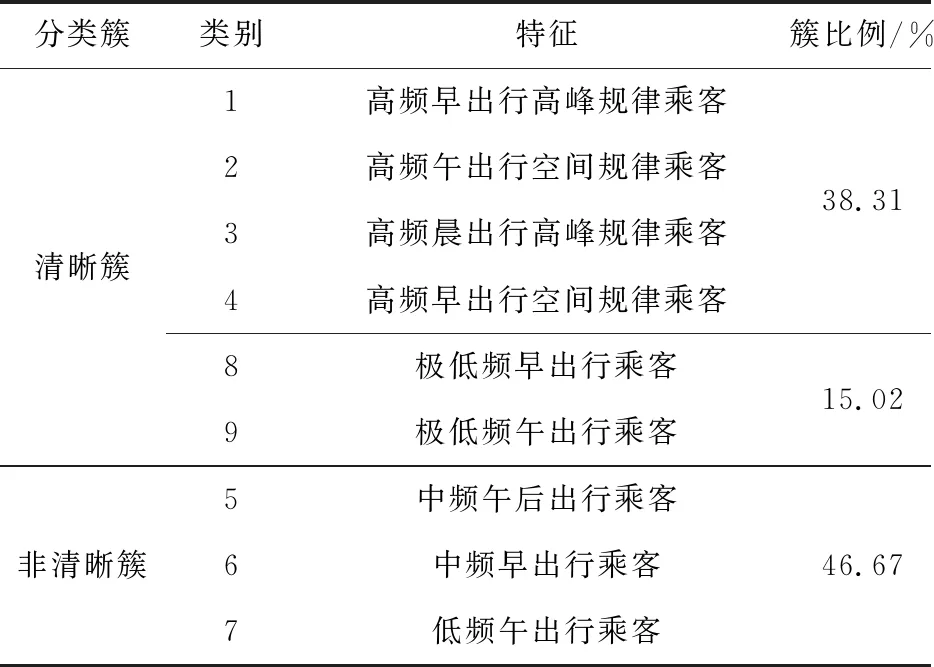
表2 乘客分类特征

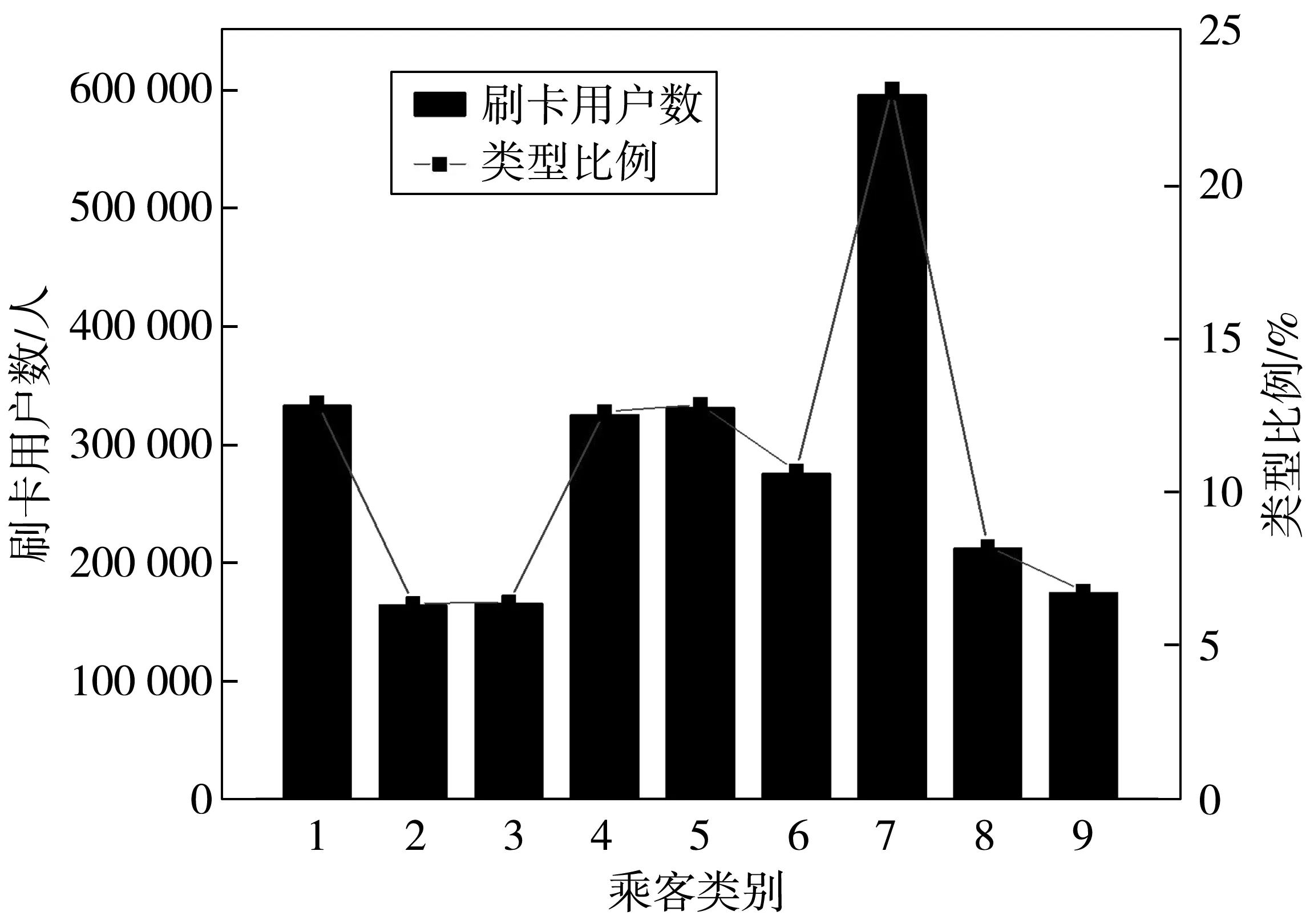
图3 各类别乘客数及所占比例

2.3 类别分析

通过比对各不同类别的乘客在乘车强度和乘车时间、空间以及高峰特性上的分布特征,可以了解各分类下的乘车规律,各类别乘客特征均有明显差异。

类别1～类别4的乘客,在乘车强度上表现具有更强的依赖性;类别5～类别7的乘客,其在空间特性和高峰特性上有不同的表现;类别8和类别9的乘客,在统计周期内仅有1 d有乘车行为。

其中类别1、类别3的乘客在空间特性和高峰特性上表现更好,表明这两个类别的乘客在乘车站点的时间空间选择上更相近,其中类别3表现更规律。类别2、类别4的乘客在首次乘车时间上有较低的稳定性,且类别2的首次乘车时间相对较晚。类别5～类别7的乘客表现为在所有统计的工作日早晚高峰中有1次以内的乘车行为,其中类别7为早晚高峰均无多于2次的乘车,且这3类乘客的日均首次乘车时间都在早上10点之后。类别8和乘车时间早于类别9,且这两类别的乘客无明显乘车强度、时间特性和空间特性,但在所有乘客中占15%。

图4为各类别乘客在日均乘车次数、日均首次乘车时间、空间特性和高峰特性的表现。

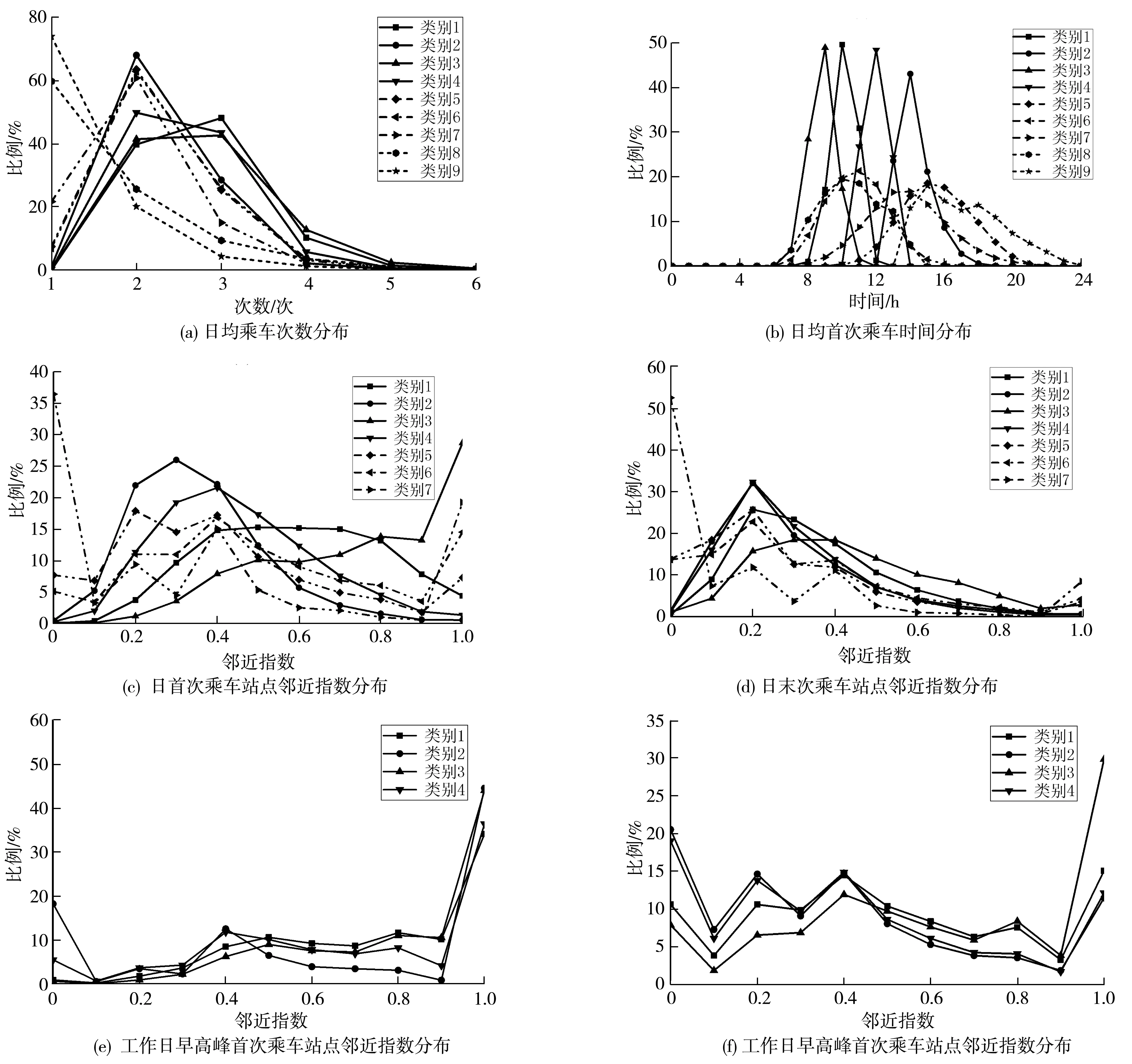
图4 不同类别乘客中的各分类特征分布情况

表3给出了不同类型乘客的聚类中心信息。

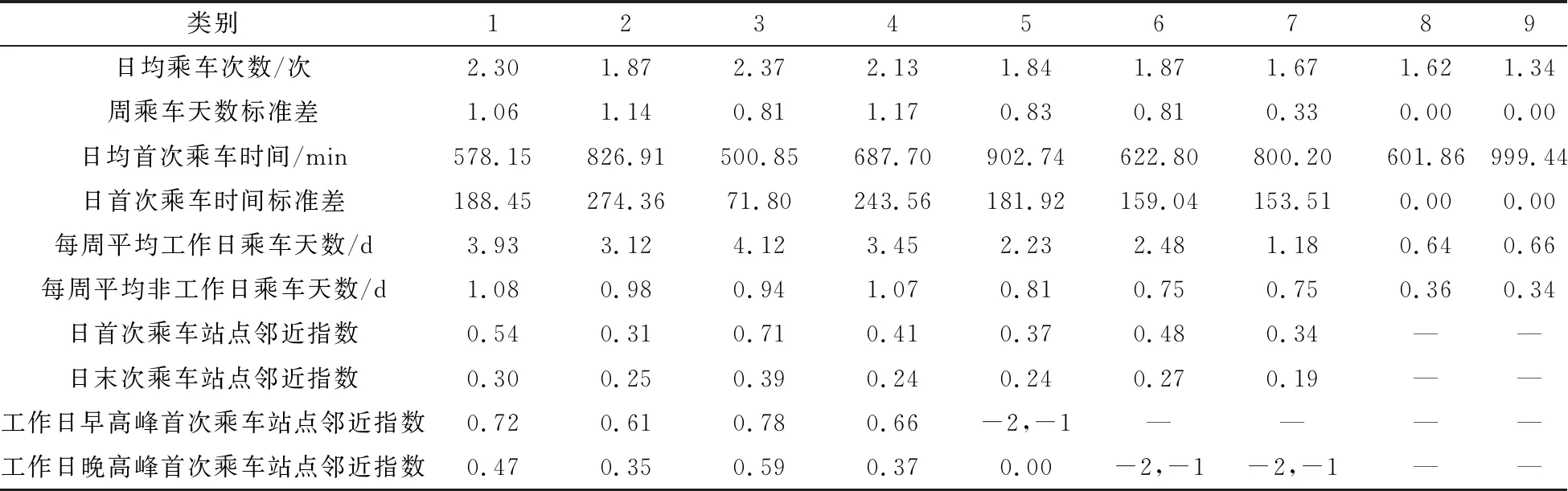
表3 乘客用户聚类结果

2.4 案例小结

笔者使用公交一票制乘客精细化分类模型可将案例乘客分成9个类别。与其他分类方法相比,有以下特点,说明该分类模型对广州市公交一票制下的乘客分类效果优良,有效性和稳定性较高。

1)应用一票制下的空间特性和高峰特性指标,仅利用上车信息实现有效刻画广州市乘客不同的乘车特性,而不需要计算乘客的出行距离、出行OD对等指标,避免了下车站点推断准确率所引起的误差。

2)对广州市的公交乘客作出9种分类情况,与以往对广州市的乘客分为3类或4类相比,分类更细致,更能全面表示现实乘客情况;对不同频率出行乘客的出行特征作出了乘车强度、时间特性、空间特性和高峰特性等的细致描述,不仅限于将时间、空间规律性进行组合或通过出行频率高低对乘客进行分类;更可有效刻画城市乘客出行特征,如案例中广州的早高峰时段相对较晚(08:00—11:00),且持续时间较长,另外乘客群体中极低频乘客有一定占比。

3)聚类效果稳定。选取每一自然周内有乘车行为的乘客,并对每周内的乘客进行类别统计,如表4。各自然周内乘客分类情况相近,数据表明分类模型有较强的稳定性。

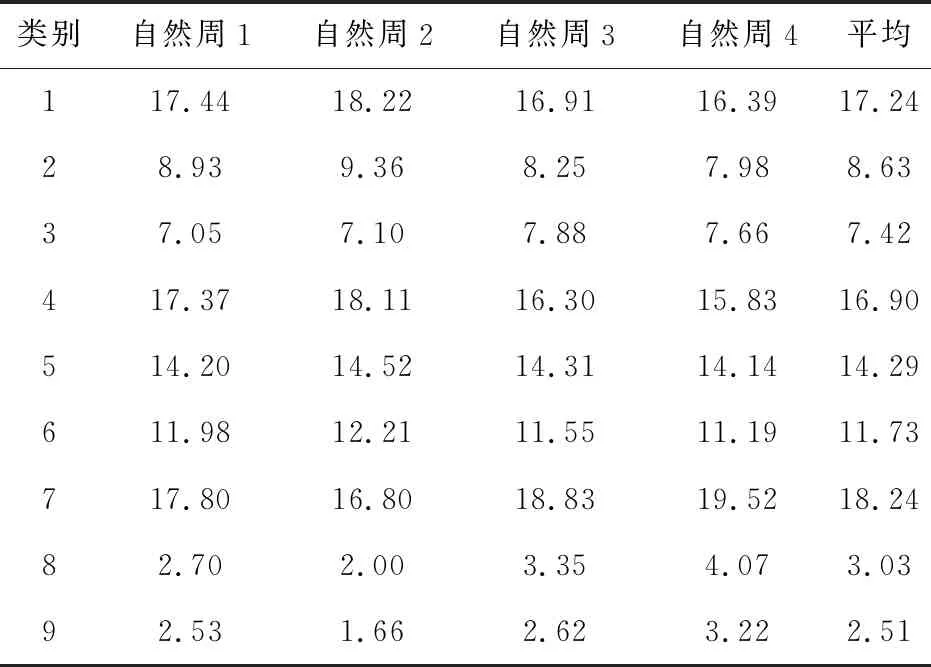
表4 各自然周内乘客分类占比情况

3 结 论

以使用公交一票制乘车用户为研究对象,通过对刷卡数据的挖掘,提出了一种针对公交一票制乘客的精细化分类方法,该方法可以有效识别乘客的乘车特征。以选取乘客的乘车强度、时间特性、空间特性及高峰特性的特征指标,以组合聚类的方式实现对乘客的精准化分类。

区别于传统的乘客分类研究,笔者所提出的分类方法存在以下几点优势:①不局限于乘客的付费方式,可应用于全类型的乘车付费方式;②针对使用一票制付费方式的公交乘车行为,与记录上下车信息的公交分类不同,补充了关于公交一票制下的乘客分类研究;③针对无下车信息的研究背景,对单一乘客的多次上车站点信息提出空间指标和高峰指标的计算方法;④对公交一票制下的乘客作出精细化分类,对由清晰簇和非清晰簇分类下的高频、中频、低频乘车用户的特征作出细致化描述,对于高频乘车用户的特征作再分类,对乘客的分类更全面;⑤公交乘客精细化分类有助于公交运营者深入了解乘客出行特征,可用于公交服务质量提升、运营优化、公交需求预测、个性化公交服务等。

后续研究可考虑距离阈值选取和时段选择对于分类效果的影响,同时基于数据拓展的基础上,采用包含位置关系的多源数据,改进分类方法,使结果更符合全群体乘客的出行规律。