基于改进人工势场算法的CT 扫描床路径规划算法
2023-05-10华宇宁
华宇宁,郜 鹏
(沈阳理工大学自动化与电气工程学院,沈阳 110159)
近十年来,国产CT 迅猛发展,其整体性能的提升是进一步提高市场占有份额的重要因素。CT 多轴运动控制系统作为CT 机的重要组成部分,其性能的提升尤为重要。 其中,CT 扫描床路径规划算法是CT 多轴运动控制系统中一个比较重要的研究课题。 路径规划是指寻求一条从起始点到目标点,能够避开障碍物的最优或次优无碰撞路径。 CT 扫描床的路径规划分为两种,分别是CT 扫描床与CT 旋转扫描架的单轴独立控制和CT 旋转扫描架与CT 扫描床的多轴联动控制。单轴独立控制指的是CT 旋转扫描架与扫描床分开运动,当扫描床移动至指定预扫点时,将位置信息反馈给CT 机固定控制单元(SCU),SCU 再控制CT 旋转扫描架动作。 此方法能较好地完成CT 扫描床的路径规划,但CT 机单次图像扫描的采集时间加长,影响CT 机的性能指标。 因此,多采用CT 旋转扫描架与CT 扫描床的多轴联动控制。 多轴联动控制指的是CT 扫描床与CT 旋转扫描架同步进行路径规划,由SCU 同时控制两者的运动状态,避免发生干涉碰撞。
目前,CT 中常用的多轴联动控制通常是通过床高与旋转扫描架倾斜角度的函数进行路径规划。 该多轴联动控制方法虽然可以完成CT 旋转扫描架和CT 扫描床的同步路径规划,但属于无时序控制,造成扫描床不能平稳运行,影响患者舒适感。 目前,主流的路径规划算法有人工势场算法[1]、遗传算法[2]、神经网络算法[3]、粒子群算法[4]、动态窗口算法[5]等。 其中,遗传算法存在计算效率低、易过早收敛等问题;神经网络算法存在收敛速度慢、易出现局部极小值等问题;粒子群算法缺乏速度的动态调节,不能有效解决一些非直角坐标系问题;动态窗口算法路径规划时的轨迹空间较小,路径平稳性较差。 与上述算法相比,人工势场算法因其计算量小、实时性好、易于实现等优点,在无人机[6-7]、AGV[8-9]、移动机器人[10]等领域应用广泛。
本文将人工势场算法应用到CT 多轴运动控制系统中完成扫描床的路径规划。 CT 旋转扫描架正倾、负倾与扫描床运动过程中产生的干涉点,视为障碍物,扫描床作为运动体,在完成路径规划时,需要避开干涉点,求得一条最优或次优的无碰撞路径。
传统人工势场算法在实际应用中会产生局部最优解问题和目标不可达问题,影响路径规划效率,或可导致路径规划失败。 国内外学者在解决上述两个问题时,一是通过修正斥力函数或引力函数解决目标不可达问题[11],二是改变运动体的势场等方法解决局部最优解问题[12-13]。 针对传统人工势场算法的不足,本文从引力距离函数、斥力距离函数及虚拟扫描床位置点解决目标不可达与局部最优解问题,提高扫描床的避障能力和路径规划的有效性。
1 传统的人工势场算法
人工势场(Artificial Potential Field,APF)算法由Khatib[14]提出并首次应用在机械臂的路径规划研究中。 该算法本质上是一种虚拟力场算法[15-16],基本思想是假设目标点和障碍物之间存在引力势场力、斥力势场力,运动体在合力的大小、方向牵引下运动。 本文将旋转扫描架运动轨迹点定义为障碍物,预扫点对扫描床的作用力定义为引力,旋转扫描架对扫描床的作用力定义为排斥力。 扫描床在虚拟力场中的受力情况如图1所示。

图1 扫描床在虚拟力场中的受力情况
1.1 引力势场
引力势场表现为预扫点对扫描床的吸引能力,引力势场力的大小是由扫描床与目标点的距离决定的。 当扫描床靠近预扫点时,距离较小,引力势场力较小,当扫描床停留在起始点附近时,距离较大,引力势场力较大,因此吸引扫描床向预扫点位置移动。 在预扫点处,扫描床受到的引力势场最小;在扫描床起始点处,扫描床受到的引力势场最大。 引力势场函数定义为
式中:Uatt代表引力势场;katt为引力势场因子;X代表扫描床所在当前点的位置坐标;Xg表示预扫点的位置;X-Xg表示当前位置与预扫点的欧氏距离。
引力函数的负梯度表达式为
1.2 斥力势场
斥力势场表现为旋转扫描架对扫描床的排斥能力,斥力势场力的大小由旋转扫描架与扫描床之间距离决定,当扫描床在旋转扫描架附近时,距离较小,斥力较大,排斥扫描床使其远离旋转扫描架;当扫描床远离旋转扫描架时,距离较大,斥力势场力较小;当距离大于旋转扫描架最大影响范围时,此时的斥力为0,将不再产生任何作用。 斥力势场函数的表达式为
式中:Urep为斥力势场;krep为斥力势场因子;X0表示旋转扫描架目前的位置;X-X0表示扫描床当前位置与旋转扫描架之间的欧式距离;d0为旋转扫描架斥力势场影响的最大范围。
斥力函数的负梯度表达式为
1.3 传统人工势场算法的局限性
采用传统人工势场算法进行路径规划可能存在目标不可达问题:当扫描床到达预扫点附近时,预扫点对扫描床的吸引力接近为零,但此时旋转扫描架对扫描床的排斥力仍然存在,导致扫描床在斥力的作用下继续运动,造成目标不可达,如图2 所示。

图2 目标不可达问题
采用传统人工势场算法进行路径规划还可能存在局部最优解问题,主要有两种:①当扫描床受到的斥力等于引力且方向相反,如图3 所示,此时扫描床停止运动,无法达到预扫点位置;②当由几组斥力组成的合力等于引力且方向相反,此时也会出现局部最优解情况,如图4 所示。

图3 局部最优解情况①

图4 局部最优解情况②
针对传统人工势场算法的不足之处,并根据CT 多轴运动控制的特性,本文通过修正引力函数、斥力函数解决目标不可达问题,通过提出虚拟扫描床位置点解决局部最优解问题。
1.4 改进的人工势场算法
1.4.1 引力函数优化
针对预扫点对扫描床引力不足的情况,当扫描床进入障碍物作用域内,将扫描床与障碍物的距离函数y1引入引力势场函数中,如式(5)所示。
式中:l为障碍物最大影响距离;l0表示扫描床与障碍物的距离。
引进扫描床与障碍物的距离函数是为了增加引力,使引力在障碍物距离缩小时迅速增大。 当扫描床与障碍物的距离大于障碍物最大影响距离时,此时引力较大,仍使用原有公式。 当扫描床与障碍物的距离小于等于障碍物最大影响距离时,此时引力越来越小,因此需要提升引力函数的大小,解决引力不足的问题。 改进的引力势场函数为
则对应的引力为
1.4.2 斥力函数优化
随着扫描床与目标点的距离越近,引力也在不断减小,此时若不对斥力进行削减修正,极易造成靠近目标点时,斥力大于引力。 在路径规划的初始阶段,扫描床受到的引力极大,易与障碍物相撞,所以斥力的变化趋势应该同引力一致。 在原有斥力函数表达式中加入扫描床与目标点之间的距离作为距离函数y2,如式(8)所示。
式中(X-Xg)为扫描床与目标点之间的欧式距离。
通过距离函数y2可以调节扫描床在预扫点位置时斥力过大的问题。
改进后的斥力势场函数为
则对应的斥力为
1.4.3 局部最优解优化
在扫描床陷入局部最优解时,判断是否到达预扫点。 若没有,则通过扫描床虚拟位置点解决局部最优解情况。
扫描床虚拟位置点定义:方向与斥力合力方向或者引力方向垂直,移动距离在行程范围内随机取值,如图5 所示。
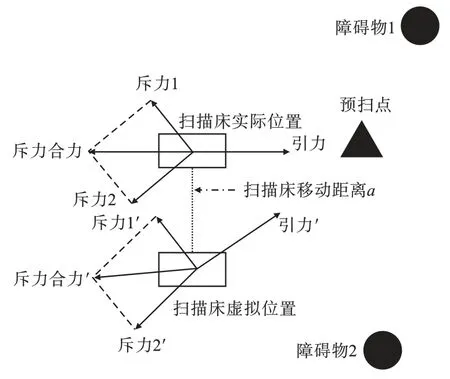
图5 局部最优解问题优化
分析图5 可知,当扫描床陷入局部最优解时,受力平衡。 当扫描床陷入局部最优解任一情况时,沿扫描床此刻位置的引力方向或斥力合力垂直方向添加一个虚拟位置点,扫描床位置沿扫描床斥力或引力垂直方向移动,移动距离为a,由虚拟位置点处扫描床的受力分析状态可得知,此时扫描床打破受力平衡状态,继续运动,待到逃离局部最优解,恢复使用扫描床实际位置。
2 仿真实验及分析
为验证改进人工势场算法在CT 多轴运动控制系统中的有效性,在MatlabR2018b 上分别进行传统势场算法与改进人工势场算法的仿真实验并进行对比分析。 模拟仿真位置参数设置:扫描床起始位置为(0,0);目标位置为(95,95);当迭代次数超过2 000 时记为超时。 四组仿真实验模型参数设置见表1。

表1 四组仿真实验模型参数设置
实验1:当扫描床受到的斥力与引力的合力为0 且斥力与引力方向相反时,此时产生了局部最优解,造成路径规划失败,无法达到预扫点,实验1 结果如图6 所示。

图6 实验1 结果
实验2:将扫描床虚拟位置点引入到传统人工势场算法中,扫描床逃离局部最优解,成功运行至预扫点位置,实验2 结果如图7 所示。
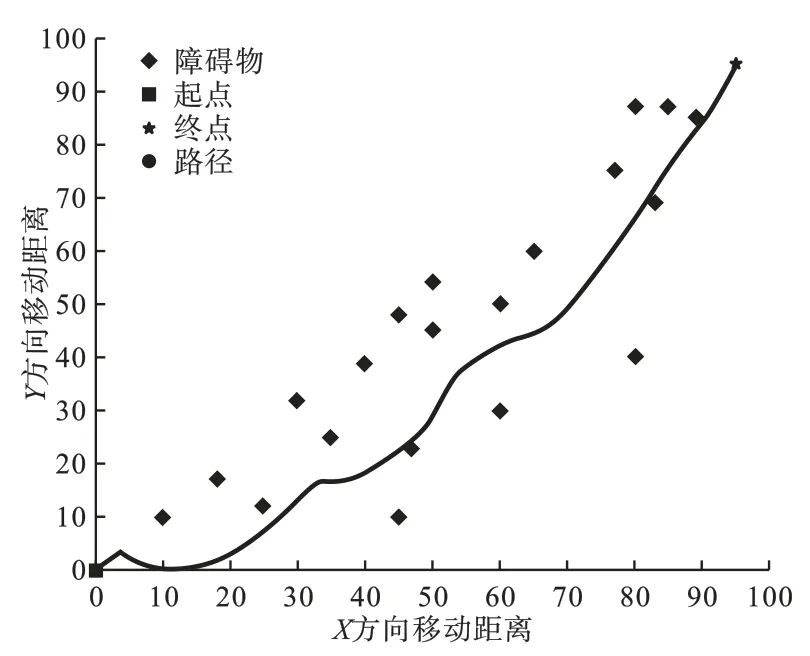
图7 实验2 结果
分析实验1、实验2 可知:在障碍物位置完全一样时,传统人工势场算法陷入了局部最优解且此时的迭代次数已经达到最大值,路径规划失败。实验2 中加入扫描床虚拟位置点,扫描床逃出局部最优解,完成了路径规划。
实验3:当预扫点位置障碍物较多时,即周围存在多个势场高点,此时扫描床在预扫点周围停止运动,造成目标不可达问题,实验3 结果如图8所示。

图8 实验3 结果
实验4:在改进的引力势场函数及斥力势场函数的作用下,扫描床越过了势场高点并成功运行至预扫点位置,实验4 结果如图9 所示。

图9 实验4 结果
分析实验3 可知,在障碍物位置完全一样时,在目标点附近,由于有障碍物的作用,传统人工势场算法受到的斥力很大,引力很小,此时扫描床并不能到达预扫点,导致路径规划失败。 分析实验4 可知,当改进了斥力函数和引力函数时,在接近预扫点时,虽然仍受到障碍物的影响,但是障碍物的排斥力远小于实验3 中障碍物受到的排斥力,此时只需要短距离绕行即可到达目标。 从实验3中其他障碍物的斥力可以看出,扫描床在远未达到预扫点时,受到的斥力远小于快抵达预扫点时的斥力;实验4 中,在未到达预扫点时,斥力远大于快抵达预扫点时的斥力。 即实验3 中扫描床受到的斥力要远小于实验4 中扫描床受到的斥力。所以,改进的人工势场算法在受到更大的斥力时,在临近预扫点位置的表现好于传统人工势场算法。 四组仿真实验结果见表2。

表2 四组仿真实验结果
由表2 可知,实验1 采用传统的人工势场算法,因其陷入局部最优解,迭代次数超过最大值,路径寻优失败。 实验2 加入了虚拟扫描床位置点,解决了局部最优解问题,迭代次数为487,完成了路径规划。 当预扫点周围障碍物较多(与旋转扫描架碰撞点)时,实验3 采用传统人工势场算法,迭代次数达到最大值时,尚未到达预扫点,路径寻优失败。 实验4 采用了改进的人工势场算法后,在迭代次数为362 次时,其寻优已结束,扫描床成功到达预扫点。
3 结论
本文针对CT 扫描床运行过程中的路径规划问题,提出了一种基于改进人工势场算法的CT扫描床路径规划方法。 本文提出的虚拟扫描床位置点方法,有效解决了CT 扫描床在运行过程中陷入局部最优解而造成CT 扫描床无法达到预扫点问题。 在引力势场函数、斥力势场函数中引进距离函数解决了CT 扫描床在预扫点附近目标不可达问题。 仿真结果表明,改进的人工势场算法能更好地完成 CT 扫描床运动过程中的动态避障。
