外部扰动下四维超混沌金融系统的完全同步问题

王仲连,郭荣伟

齐鲁工业大学(山东省科学院) 数学与统计学院,山东 济南 250353

混沌就是某些具有确定性的非线性系统,在一定参数范围内能给出非周期的、表面看来很混乱的输出,即来源于确定的体系的无规则运动。混沌现象揭示了在确定性和随机性之间存在着由此及彼的桥梁,这在科学观念上存在着深远的意义。越来越多的学者从不同的角度来研究混沌系统的同步问题,从两个相同系统的同步问题推广到两个不同系统的同步问题,甚至是两个不同维数的混沌系统之间的同步问题[1-4]。这里需要重点指出的是上述研究结果大部分没有考虑系统所受到的外部扰动,或者考虑的只是在某种意义下的有界扰动。事实上,对于一个系统来说,外部扰动是不可能完全避免的,并且有时系统所受到的扰动并不是有界的,比如在某一时刻系统受到了外部脉冲信号的干扰。因此,研究系统在外部干扰下的控制问题不仅具有重要的理论意义,而且具有重大的应用价值。UDE方法[5-7]是近年来处理系统中模型不确定性和外部扰动的一个非常好的方法,对于一些有界的外部扰动,该方法能实现精确的估计,从而实现精确跟踪或者渐近稳定。但是,对于某种类型的无界扰动,该方法只能给出鲁棒性的结果。受UDE思想的启发,通过寻找合适的函数进行卷积的方法对两种类型的扰动分别设计了相应的滤波器,均实现了控制目标。

四维超混沌金融系统[8]是一个的重要的经济学模型,其系统模型有四个变量,即货币、生产、劳动力和股票。该模型自提出以来,已经取得了大量的研究成果[9-12]。然而,正如上面所介绍的,外部干扰的影响,特别是在无界的外部干扰的影响,并没有被考虑。 因此,研究在无界的外部扰动下的四维金融超混沌系统的完全同步问题是非常重要和迫切的。

1 预备知识

定义1[1]:考虑如下的混沌系统

其中,x∈Rn是系统的状态,g(x)是连续的向量函数。

设系统(1)是主系统,则相应的从系统为

其中,y∈Rn是系统的状态,g(y)是连续的向量函数,B∈Rn×r是常矩阵,r≥1,u∈Rr是带设计的控制器。

再令E=y-x,则误差系统为

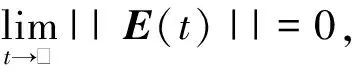
2 问题描述

考虑在外部扰动干扰下受控的四维超混沌金融系统[8]

其中,x∈R4是系统的状态,f(x)∈R4是连续的向量函数,d(t)∈R4是外部扰动,即

外部扰动d(t)有两种情况:

情况1:

情况2:

其中A,C是未知非零常数。

令系统(4)为主系统,则从系统为

其中,y∈R4是系统的状态,f(y)∈R4是连续的向量函数。

本文的主要目的是设计控制器u∈R使得

即主系统(4)和从系统(8)达到了完全同步。

3 主要结果

为了实现系统对外部干扰的抑制,受UDE思想的启发,对常数类型的有界扰动和多项式乘以三角函数类型的无界扰动分别设计了相应的滤波器,并实现了对上述干扰的精确抑制。

定理1 如果常数类型的有界扰动d1(t)=C,其中C是未知常数,则设计的滤波器为

其中,k是一个正数。

证明:当t→∞时

定理2 如果无界的外部扰动为d1(t)=Atsin(t),其中A是未知常数,则设计的滤波器为

证明:因为

而计算如下卷积得到

定理3 考虑主系统(4)和从系统(8)对于公式(6)所表示的有界扰动,设计的同步控制器如下:

u=us+ud, (11)

其中,

us=k(t)(1,0,0,0)E=k(t)E1, (12)

E=x-y,Gf(s)见公式(9),

证明:令E=x-y,则误差系统为

其中,

注意到,若E1=0,则下面的系统

是渐近稳定的。

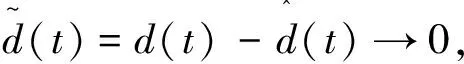
再对下面的方程两边取Laplace变换

整理可得到公式(13)中的ud。

对于第二种情况的扰动,证明过程类似,本文直接给出如下的结论。

定理4 考虑主系统(4)和从系统(8)对于公式(7)所表示的无界扰动,设计的同步控制器为

u=us+ud, (18)

其中us见公式(12),

E=x-y,Gf(s)见公式(10),k(t),F1(y,E)见公式(14)。

4 数值仿真

情况1:公式(6)所示的有界扰动。

选择主系统(4)的初值为x(0)=[1,2,-3,4],从系统(8)的初值为y(0)=[5,-2,3,2],反馈增益的初值k(0)=-1,d1(t)=100。MATLAB仿真结果见图1、图2、图3。

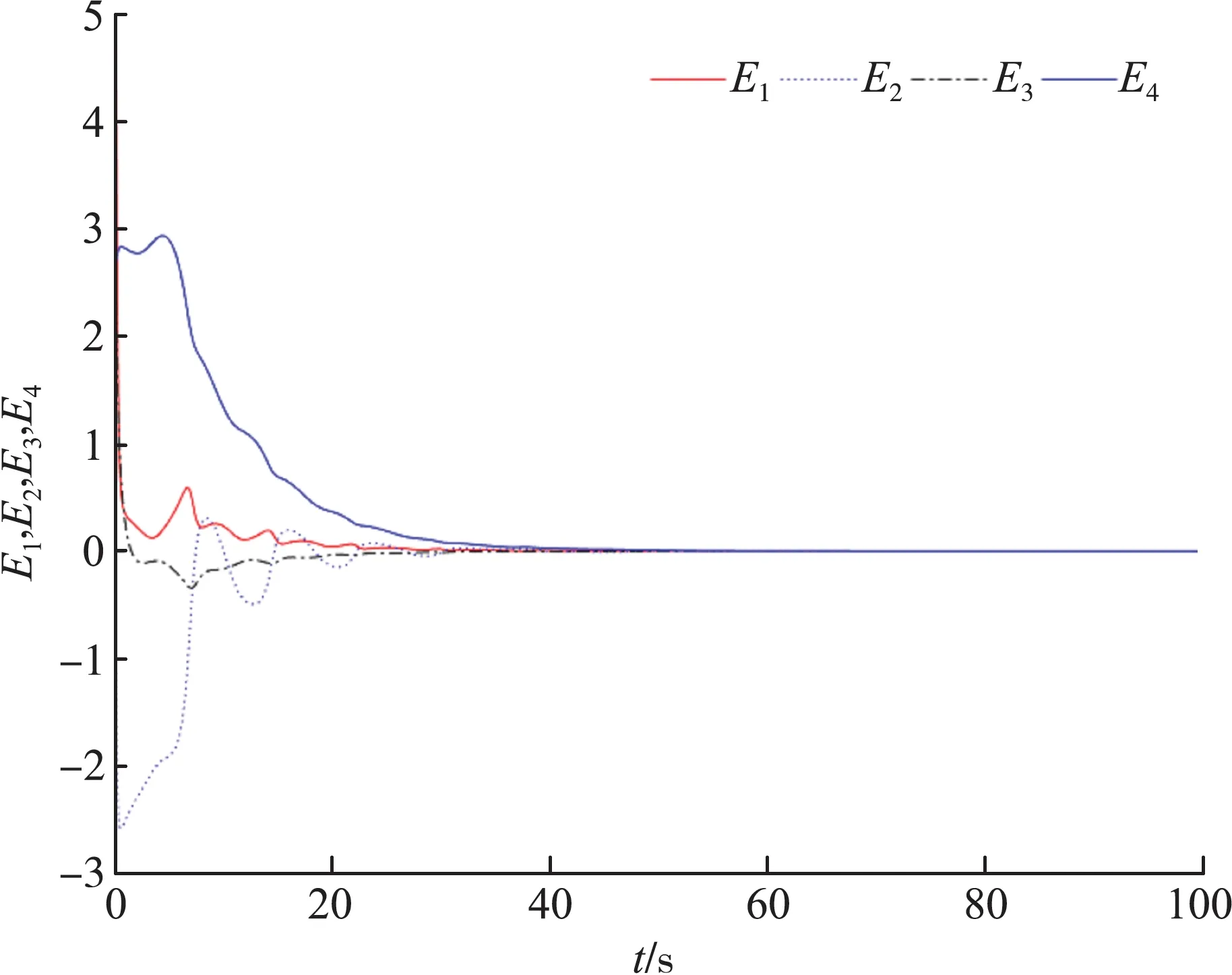
图1 误差系统渐近稳定

图2 动态反馈增益k(t)渐近收敛到一个合适的常数

图渐近收敛到d1(t)

情况2:公式(7)所示的无界扰动。

选择主系统(4)的初值为x(0)=[3,2,5,2],从系统(8)的初值为y(0)=[3,2,5,2],反馈增益的初值k(0)=-1,扰动d1(t)=10tsint。MATLAB仿真结果见图4、图5、图6。

图4 误差系统渐近稳定

图5 动态反馈增益k(t)渐近收敛到一个合适的常数

图渐近收敛到d1(t)

5 结 论

本文用基于扰动估计器的控制方法研究了四维混沌金融系统的完全同步问题。受UDE思想的启发,对于常数类型的有界外部扰动和多项式乘以三角函数类型的无界外部扰动,分别设计了相应的滤波器,并设计了相应的控制器,从而实现了该系统的完全同步问题。首次解决了在某种无界的外部扰动下四维超混沌金融系统的完全同步问题。数值仿真结果验证了理论结果的正确性和有效性。

获得的理论结果经过适当地修改可推广到研究一般的非线性系统的干扰抑制问题,为研究非线性系统的各种控制问题提供了理论支持。