机器人运动学模型参数修正
2023-05-10南京航空航天大学航空学院闻了然张方
南京航空航天大学航空学院 闻了然 张方
在工业自动化的大背景下,企业对工业机器人的精度要求越来越高。为了减少机器人在制造、安装、测量、连杆变形等因素下造成的定位误差,本文以一六轴工业机器人为研究对象,提出一种基于最小二乘法和机器人正运动学的运动学模型参数修正法,通过对比分析末端执行器的位置信息,对现有的运动学模型进行参数修正,从而降低工业机器人的模型误差,为机器人后续的轨迹规划工作提供了帮助。
随着科学技术的不断更新与发展,工业机器人在搬运、喷釉、弧焊等方面有着十分突出的贡献,对末端执行器的精度要求也变得更高[1]。工业机器人的定位精度决定着机器人工作性能的优劣。然而在工业生产过程中,工业机器人不可避免的存在误差,这些误差主要分为两个部分:制造、安装以及长时间工作导致的磨损和变形引起的几何误差和温度、机器自重等因素导致的非几何误差。上述的几种误差最终都会在末端执行器的位姿信息中体现出来,而位姿信息又与机器人的运动学模型相关。为了降低机器人的定位误差,需要对原有的运动学模型进行修正。
当前机器人运动学模型的建模方法普遍采用的是1955 年Danevit 和Hartenberg 提出的D-H 建模法[2]。而为了降低工业机器人定位精度误差,通常会对末端执行器进行反馈检测,实现全闭环控制[3,4]。这种方法虽然可以达到很高的精度,但是计算复杂,成本投入较高,不适用于焊接等精度要求不是特别高的工作。
针对该问题,本文利用D-H 建模法得出的变换矩阵,建立末端位姿信息与各运动学模型参数的关系式,并提出一种基于最小二乘法的改进模型修正法。在误差允许范围内仅测量末端在不同关节角下的理论位置和实际位置,而忽略姿态信息,完成运动学模型的参数修正,从而大大降低了运算难度,同时满足了精度要求,具有良好的工程实用性。
1 机器人运动学分析
1.1 机器人基本结构及D-H 参数
机器人可以视作由一系列刚体通过关节连接而成的一个运动链,通常境况下,我们称这些刚体为连杆,而关节将两个相邻的连杆连接起来。在进行机械臂结构设计时,通常优先选择仅具有一个自由度的关节作为连杆的连接方式,即转动关节或移动关节[5]。
本文以钱江QJRH4-1A 型机器人为例,从底部固定的基本连杆开始从下往上开始编号,第一个可动连杆为连杆1,直至连杆6。同时,在工作空间中,为了使末端执行器拥有6 个自由度,需要为机器人配置6 个旋转关节,前3 个主要确定位置,后3 个主要确定姿态。
一般情况下,在进行机器人D-H 参数设计时,需要考虑连杆长度、连杆转角、连杆偏距和关节角4 个参数[6]。
参考实体结构图建立机器人连杆坐标系,其中基坐标系在1 轴位置,4-6 连杆坐标系均在5 轴上,具体如图1 所示。

图1 钱江QJRH4-1A 型机器人连杆坐标系Fig.1 Linkage coordinate system of Qianjiang QJRH4-1A robot
通过对官方给出的模型图进行测量,该机器人的D-H 参数表如表1 所示。
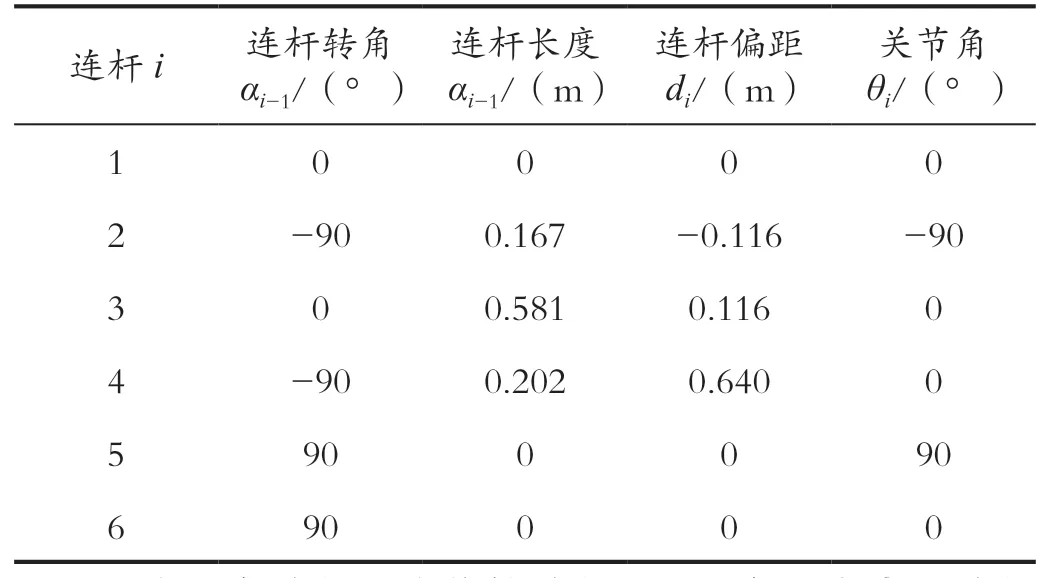
表1 钱江QJRH4-1A 型机器人D-H 参数表Tab.1 Table of D-H parameters of for Qianjiang QJRH4-1A robot
因为6 个关节均为旋转关节,D-H 参数表中,关节角一栏数值为机器人在零位时的数据,其本身是变量,取值范围不能超过限位角。
1.2 机器人正运动学
正运动学的主要思路是已知机器人各关节角,计算求解出末端执行器在基连杆坐标系下的位置和姿态[7]。参考图1 标识的各连杆坐标系位置,确定基连杆坐标系为坐标系{0},原点为1 轴所在位置,之后根据D-H 参数表确定各连杆坐标系的关系。任意2 个连杆坐标系之间的关系可用四阶变换矩阵T 来表示。对变换矩阵进行分块,左上角三阶矩阵为旋转矩阵R,右上3×1 矩阵代表后一个坐标的原点在前一个坐标系下的位置坐标,最后一行为固定值。具体矩阵如公式(1)所示:
为了方便书写,公式(1)中对三角函数进行如下简化,后文同理:
对于本文机器人,共设有6 个连杆,将D-H 参数带入公式(1),可得末端执行器在基连杆坐标系下的变换矩阵如公式(2)所示:
其中:
利用机器人正运动学,机器人末端的位置和姿态信息可以与连杆转角、连杆长度等参数一一对应。这为后续的运动学模型参数修正提供了理论依据。
2 运动学模型参数误差修正
2.1 最小二乘法原理
最小二乘法是一种数学优化技术。它通过最小化误差(真实目标对象与拟合目标对象的差)的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求出未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小[8]。这种方法理论成熟,计算简便且工程适用性强,可用来对未知参数进行辨识,其具体估计过程如图2 所示。
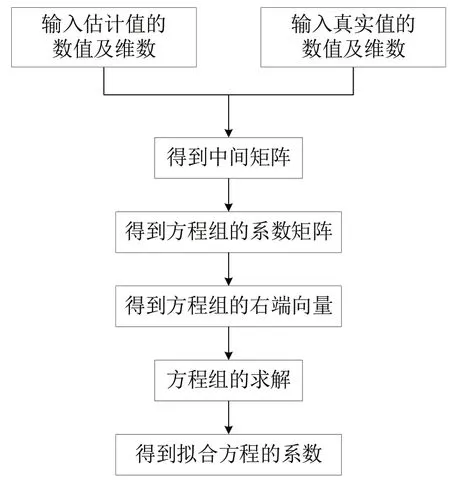
图2 最小二乘法示意图Fig.2 Schematic diagram of least squares method
最小二乘法的具体思路如下所示:令
设有m组实际值y,则有m组误差值:
因为最小二乘法的约束条件是保证函数的误差平方和最小,所以误差向量越小,最小二乘法最终拟合出来的数据质量就越高。其具体估计过程如图2 所示。
在这里假设最小二乘法的模型为:
在该模型中θ是变量,x是输入的定量,y是输出拟合值,即预测量。定义误差:
可知误差平方和:
上式可用以下方程组来表示,如公式(3)所示:
显然该方程组可转换为矩阵形式,如公式(4)所示:
该矩阵可简化为如公式(5)所示:
于是最小二乘法的表达式可简化为如公式(6)所示:
研究数据纳入SPSS17.0软件分析,计量资料以(± s)表示,采用t检验;计数资料用(%)表示,采用χ2检验,P<0.05差异有统计学意义。
满足该式的向量即为最小二乘法的解。显然,该误差函数是关于θ的多元二次函数方程组,要求取最小值,则只需令其一阶导数为0 即可。将上式对θ求导,并令其为0,可得到如公式(7)所示:
再变形可得到如公式(8)所示:
公式(8)就是最小二乘法所求的向量。
2.2 工业机器人运动学模型修正
由公式(2)可知,因为D-H 参数与变换矩阵相互独立,工业机器人的运动学模型满足最小二乘法要求的变量相互独立原则,考虑机器人的焊接精度要求,这里只考虑机器人末端的位置误差,不考虑姿态误差,从而大大减少了计算难度[8]。结合公式(2)给出的变换矩阵,机器人末端的位置信息由以下参数决定,如公式(9)所示:
显然影响末端位置的D-H 参数只有连杆长度和连杆偏距,对公式(9)进行偏微分可得如公式(10)所示:
根据2.1 节和公式(10)可设参数矩阵X,位置误差矩阵参数误差矩阵θ,其中:
接着多次测量机器人在任意关节角下末端直角坐标系实际值,并计算在各个关节角下末端的理论坐标值与误差。将计算得出的误差值列为矩阵放置在公式(4)右端,最终把所有矩阵带入公式(8)计算即可,位置误差矩阵具体为:
3 试验数据与分析
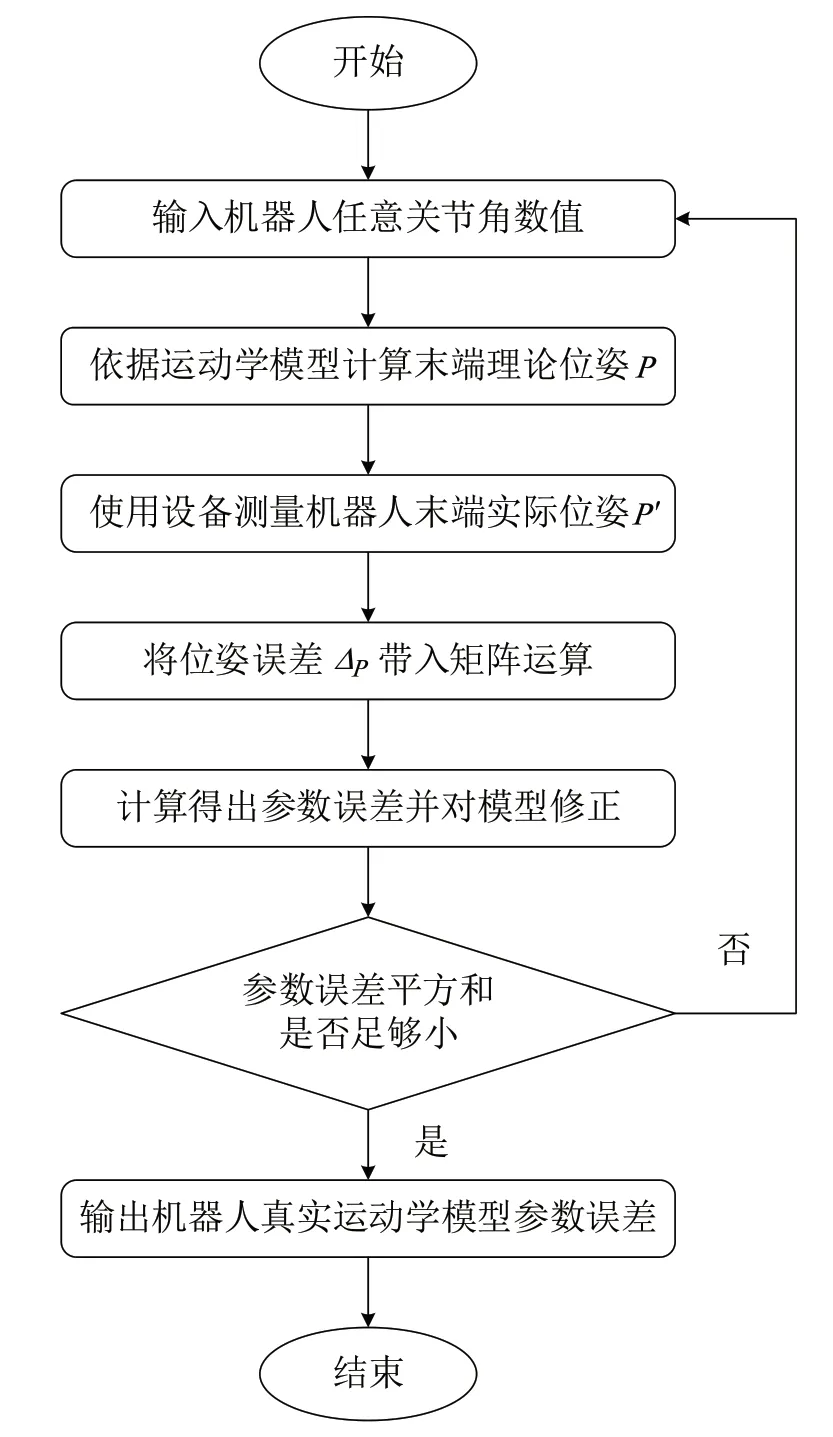
图3 运动学模型修正流程图Fig.3 Kinematic model correction flow chart
钱江QJRH4-1A 型机器人是一个焊接机器人,对末端位置的误差要求在1mm 以内。试验过程中首先使用上位机关节角示教模式使各轴旋转到任意位置并记录当前关节角度值,之后通过激光跟踪仪测量得到末端的位置信息并与计算得出的理论结果进行作差,最后将该数据输入程序中计算参数误差。试验现场如图4 所示。

图4 试验现场Fig.4 Experimental site
试验总共测量了10 组不同的关节角下末端的坐标值,之后将上述数据代入程序计算可得参数误差矩阵为:
θ=[-0.901 -1.441 2.673 -0.671 0.114 0.234 0.215 -0.098 0.505 0.273 -0.226 -0.027]
为了验证修正之后的运动学模型,将这10 组关节角代入新的D-H 参数并进行正运动学求解,与测量的末端位置进行比较,具体数据如图5 所示。修正后的平均定位误差从1.396mm 减少到0.582mm,小于1mm,符合焊接工程要求。

图5 机器人末端定位误差值Fig.5 Positioning error value of robot end
4 结论
为了提高机器人末端执行器的定位精度,本文首先对机器人进行了运动学建模,用连杆长度、连杆转角、连杆偏距和关节角4 个参数与机器人的末端位姿信息建立了对应关系。之后集合最小二乘法,通过多次测量与计算,对机器人的运动学模型进行了修正,使其定位误差降低在1mm 以内,同时也为后续的机器人轨迹规划工作提供了帮助。
