考虑轮胎非线性特性的分段线性化处理

张文静，张丽萍

（辽宁工业大学 汽车与交通工程学院，辽宁 锦州 121000）

随着近代工业的快速发展，四轮转向（Four Wheel Steering, 4WS）汽车的操纵稳定性研究愈发深入。朱亚伟等[1]通过仿真研究发现4WS 汽车相对于前轮转向汽车提升了汽车的操纵稳定性。张庭芳等[2]针对线控转向车辆的操纵稳定性问题提出了改进型的滑膜变控制策略，有效提高了汽车的操纵稳定性能。然而，考虑轮胎的非线性特性是极限工况下研究四轮转向汽车能否发挥其操纵稳定性非常重要的一环[3]。WANG 等[4]通过考虑控制输入和轮胎非线性，建立了4WS 路径跟踪T-S模糊模型，以提高汽车的操纵稳定性。

根据研究经验，如果用线性控制理论直接处理轮胎模型的非线性表达式是很困难的，并且也很难在车辆上进行应用。因此，本文采用“魔术公式”轮胎模型，从考虑轮胎的侧偏特性入手，将轮胎的侧偏特性进行了分段线性化处理，获得拟合后的分段线性轮胎模型公式，通过权函数将两段轮胎模型公式联立起来。所得结果通过MATLAB/ Simulink 进行验证。这样轮胎的非线性特性问题既得到解决，又减少计算量，使后续研究4WS 汽车的操纵稳定性更加合理。

1 魔术公式轮胎模型建立与分析

1.1 4WS 汽车二自由度动力学模型的建立

研究表明，二自由度动力学模型是研究汽车操纵稳定性的基本模型，其在线性范围内的精度可以反映大多数日常驾驶条件下车辆操纵稳定性的基本特征，即横向加速度小、方向盘转角小以及行驶速度正常等特征。二自由度车辆模型的转向原理如图1 所示。

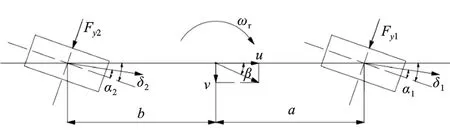
图1 4WS 汽车二自由度动力学模型

根据图1 可以列出4WS 汽车二自由度动力学方程：

式中，β为侧偏角；m为汽车的质量；Iz为汽车绕z轴的转动惯量；u为行驶速度；a、b分别为前后轴至质心的水平距离；δ1、δ2分别为前后轮的转向角；k1、k2分别为前后轮的侧偏刚度；Fy为y方向的合力；Mz为z方向上的合力力矩；ωr为横摆角速度。

为了使后续建模方便，将式（1）整理成状态方程的形式。其中状态变量为X=[β ωr]T，输入向量为U=[δ1δ2]T，系统输出向量为Y=[βωray]T。假设汽车匀速行驶，状态方程可表示为

整车相关参考系数如表1 所示。

表1 相关车辆模型参数表

1.2 轮胎侧偏特性分析

1.2.1 “魔术公式”轮胎模型

在不同的轮胎模型中，“魔术公式”模型可以用同一个公式来表示轮胎的不同力学性能，具有拟合精度高的优点。图2 为轮胎受力分析图。

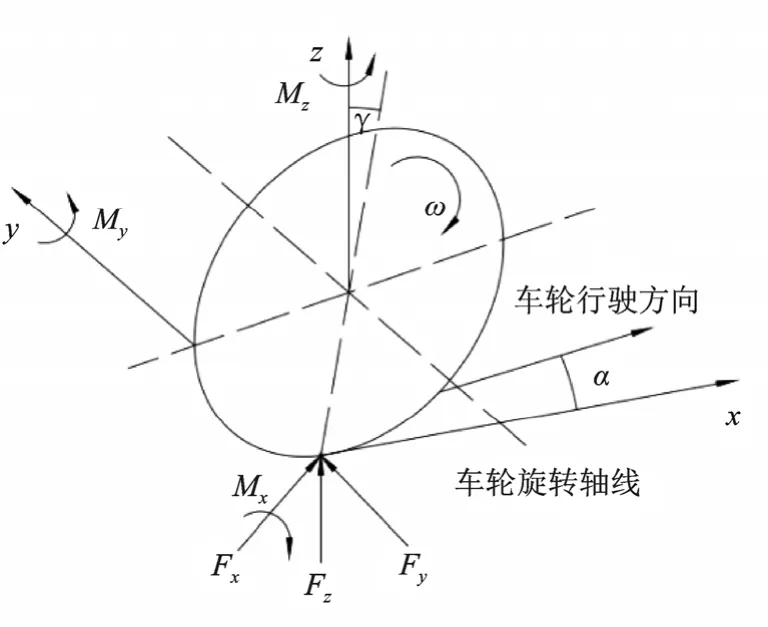
图2 轮胎受力分析图

对轮胎进行受力分析，其中，α为侧偏角；Fx为纵向力；Fy为侧向力。

轮胎的纵向力和侧向力用魔术公式表达为

式中，By为刚度因子；Cy为形状因子；Dy为峰值因子；Ey为曲率因子；αy为侧偏角自变量；α为轮胎偏角；Svy为垂直漂移；Gys为比例因子；Svys为滑动率引起的偏移。

轮胎的侧向力学特性曲线可以在MATLAB 中搭建轮胎的侧向力学模型得到，所得曲线如图3所示。

图3 魔术公式轮胎模型侧向力学特性曲线

由图3 可知，轮胎侧向力与侧偏角的关系有线性和非线性两种，且呈线性关系的范围很窄，基本在-3°～3° 以内。当侧偏角小于-3° 或大于3°时，侧向力增长的速度逐渐变缓，直到稳定在某一定值上。此时，轮胎的侧向力学特性基本不会再改变[5-6]。

1.2.2 魔术公式轮胎模型的分段线性化处理

根据轮胎侧向力与侧偏角的关系，为了更好地处理轮胎侧偏特性曲线，将轮胎侧偏特性曲线分为两段区域，即线性区域和非线性区域[7]，并将区域分界线即为α=3°，如图4 及表2 所示。

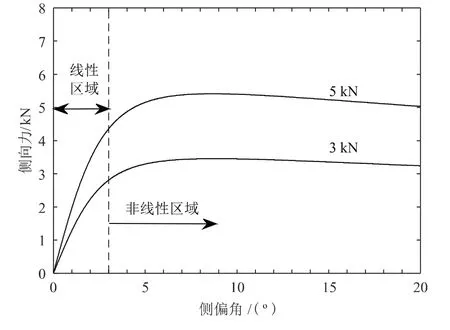
图4 轮胎侧向力特性曲线及分区

表2 侧偏特性曲线状态表

基于“魔术公式”轮胎模型，本文选取出作α∈(3°,10°)为离散数据点。同时车辆处在轮胎侧偏角大于10°的情况在实际行驶过程中比较少见，所以忽略侧偏角大于10°的非线性区域。轮胎非线性区域的侧偏刚度为区域内α∈(3°,10°)计算出的侧偏刚度。

对非线性区域的轮胎侧偏刚度拟合计算采用最小二乘法。求一组待定系数的值为最小二乘法的目标，故定义为式（4）：

根据最小二乘法的定义，将分区后的轮胎侧偏刚度利用MATLAB 进行拟合计算，并得到计算结果，其中在线性区域中拟合后的前轴侧偏刚度为k11=-199 80 N/rad，拟合后的后轴侧偏刚度为k21=-18 660 N/rad。而在非线性区域中拟合后的前轴侧偏刚度为k21=-102 430 N/rad，拟合后的后轴侧偏刚度为k22=-81 808 N/rad。

由式（2）可知，汽车系统状态空间方程的控制结构矩阵均取决于前后轴侧偏刚度的值。那么在轮胎的线性区域，此时的侧偏刚度等于前后轴在线性区域拟合后的侧偏刚度，则此时系统微分方程为

在非轮胎线性区域内，此时的侧偏刚度等于非线性区域拟合后的前后轴侧偏刚度，则此时系统微分方程为

引入跟随轮胎侧偏角变化的权函数从而将式（5）、式（6）所表述的二自由度车辆动力学模型联立[3]，定义如下：

式中，ω1为轮胎线性区的权函数；ω2为轮胎非线性区的权函数；两个权函数可以用图5 表示。取α1=2°，α1=8°，αt取前后轮胎侧偏角平均值。

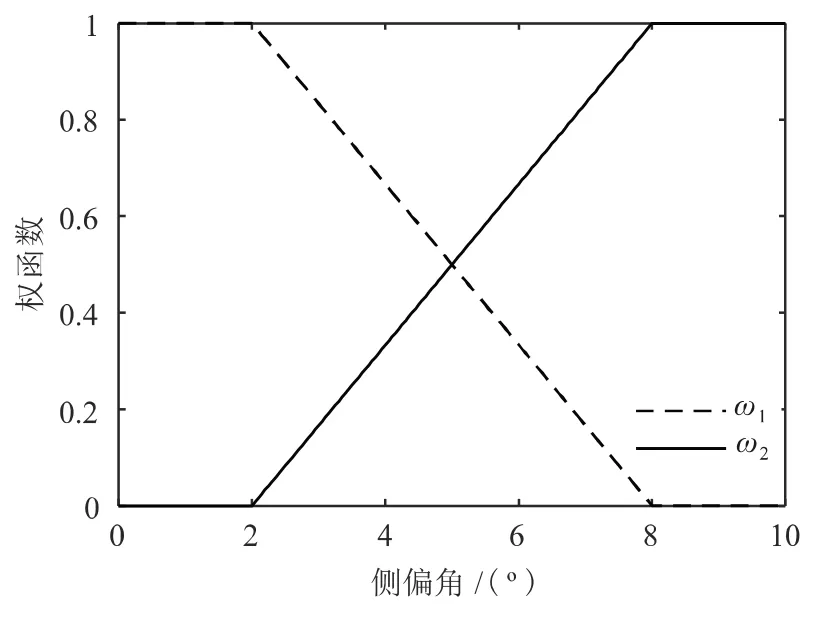
图5 权函数随轮胎侧偏角变化的曲线

当轮胎侧偏角大于0°时，在轮胎侧偏角变化整个区域，轮胎侧偏力的表达式可以列为线性区和非线性区的轮胎侧偏刚度和权函数之和，即

式中，Fy为轮胎侧偏力；αi(i=r, f)为前后轮胎侧偏角；αf1为分段线性选取的分界点。将线性区域微分方程和非线性区域微分方程联立可得

1.3 仿真验证

为了验证选取的权函数是否合理，对单胎载荷3 kN、5 kN 和7 kN 的侧偏刚度变化曲线与魔术轮胎公式侧偏刚度曲线进行对比分析[8]，仿真结果如图 6—图8 所示。

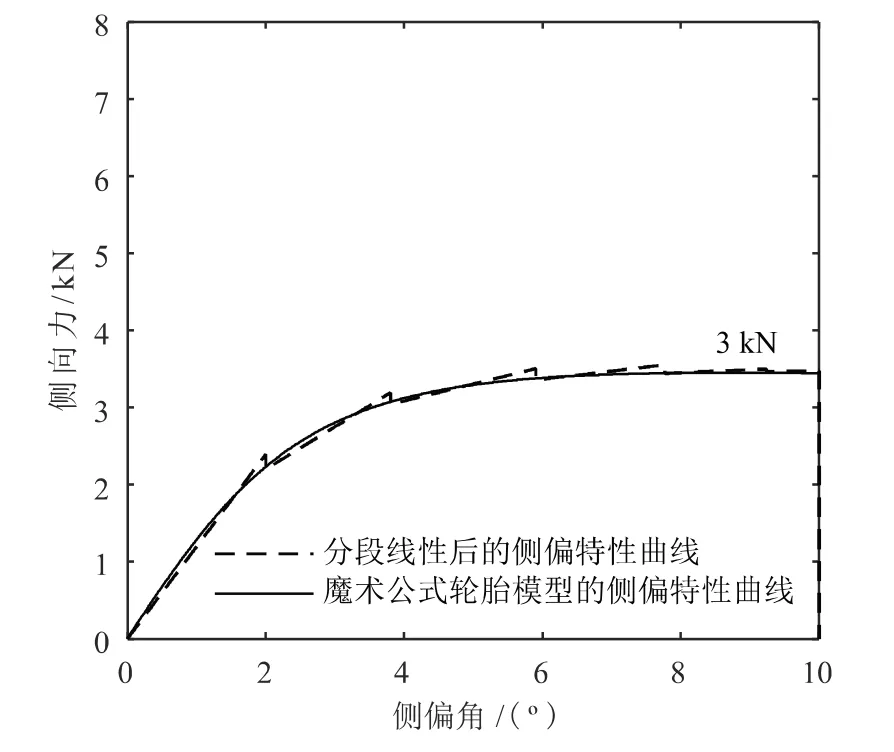
图6 单胎载荷3 kN 的分段线性模型侧偏特性与魔术轮胎式模型侧偏特性对比曲线

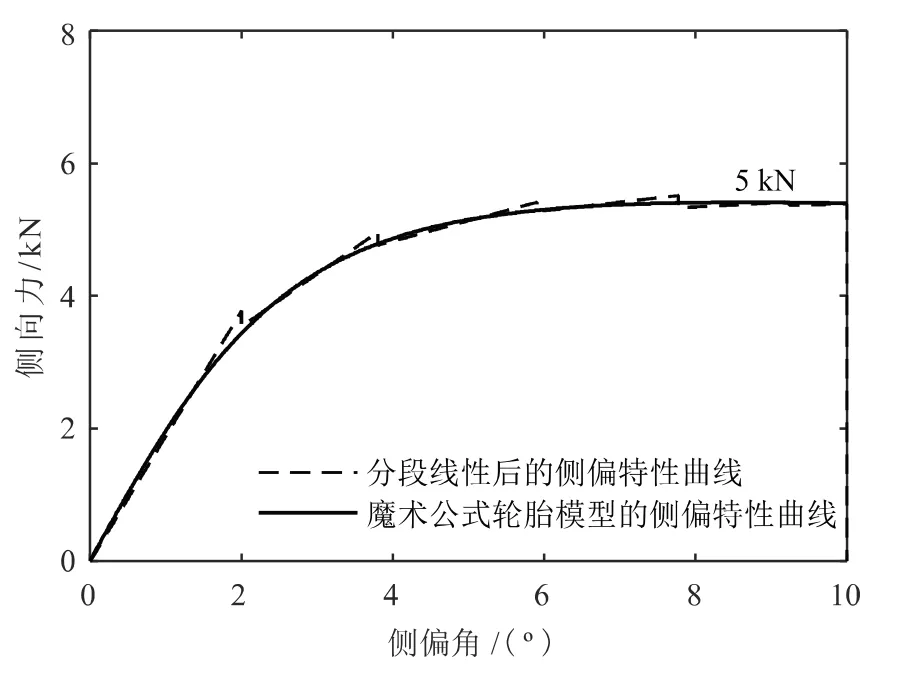
图7 单胎载荷5 kN 的分段线性模型侧偏特性与魔术轮胎式模型侧偏特性对比曲线

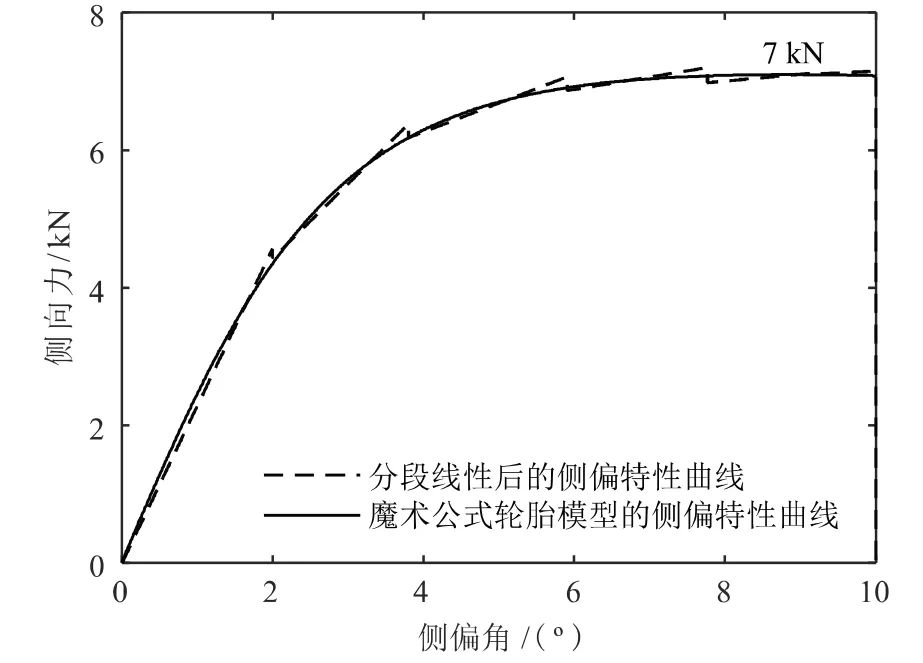
图8 单胎载荷7 kN 的分段线性模型侧偏特性与魔术轮胎式模型侧偏特性对比曲线

从图上可以看出轮胎侧偏角在10°以内，由权函数加权后的侧偏刚度曲线与魔术轮胎公式的侧偏刚度曲线变化趋势基本一致，表明对轮胎侧偏刚度曲线划分线性和非线性区域并由此引入权函数进行加权分析是比较合理的。

2 结论

以上针对汽车轮胎车侧偏特性的特点，建立分段线性的轮胎模型，由于分段线性轮胎模型与魔术公式轮胎模型非常接近，且分段线性轮胎模型需要的参数却很少，通过建立分段线性轮胎模型有效降低了轮胎模型的复杂程度，减少了计算量。且汽车轮胎侧偏角大于10°的实际行驶情况比较少，即使存在这种情况，在一定程度上也能够很好地表达轮胎侧偏力的变化。因此，该模型的建立更加接近车辆的实际使用情况，在汽车稳定性控制中具有一定的应用价值。