基于变指数趋近律的线控转向滑模控制

付 旭，刘亚莉，李舒欣，朗悦茹

（长安大学 汽车学院，陕西 西安 710064）

近年来，自动驾驶汽车的智能底盘技术研发进展成为关注的重点，其中线控转向技术由于易实现集成控制而逐渐受到重视[1]。线控转向关键技术包括变传动比技术、稳定性控制技术、转角跟踪技术。其中变传动比技术是指可自由设计期望的转向传动比，通过电子控制单元（Electronic Control Unit, ECU）实现数字信号和电信号的运放计算输出到转向执行器，保证汽车转向过程中的转向灵敏性和平稳性。线控转向是智能底盘域控制的组成部分，也是横纵向协调控制的计算平台，置换了方向盘和前轮系统之间的机械连杆，代之以传感器、执行器和ECU，实现可变传动比的设计理念。

1999 年TAJIMA J[2]首次提出理想变传动比与稳态横摆角速度增益之间的关系后，国内外学者对可变传动比及车辆稳定性控制策略进行了深入研究。其中第一类研究主要是以模糊控制为基础的专家系统设计[3]，考虑方向盘、车速及车辆运行状态进行控制算法优化，得到结果接近理想传动比，但难以脱离专家建议；第二类研究以车辆动力学为基础，综合考虑固定横摆角速度增益、固定侧向加速度增益、固定侧倾角增益及驾驶员操纵稳定性综合评价指标，进行传动比曲线拟合算法的最优化[4]，提高曲线精确性。但对稳定性影响工况考虑不全面，忽略了轮胎的非线性特性；第三类以考虑路面附着系数突变等外界因素，对车辆行驶的复杂时变、强非线性系统进行多次试验，建立离散增益值拟合曲线[5]，将稳定性扩展到变传动比设计中，使轮胎进入非线性区域时进行稳定性控制确保变传动比的有效性。

目前对车辆前轮转角的决策主要有基于汽车运动状态的前馈控制或反馈控制[6]，采用附加转向角的概念对输出转角进行更正，确保线控转向在满足驾驶员操作特性的前提下，符合行车稳定性要求。滑模控制器在研究领域也得到广泛使用，其高响应速度、强鲁棒性特质、易于实现的物理结构可以有效克服非线性系统的响应和精度问题。文献[7]基于滑模控制器的设计消除了系统参数不确定性和路面条件变化的条件对转向性能的影响，但文章过于关注控制器的理论研究，对车辆动力学性能对控制器的影响考虑尚存在弊端。在转角跟随技术方面常见的比例积分微分（Proportion Integral Derivative, PID）控制算法稳定性较差、调参复杂、应对极端工况响应较差，在此基础上大量能解决复杂系统控制精度问题的非线性PID 控制方法得以研究。线控转向具有许多优点，但仍有一些尚在研究中的技术和安全相关挑战有待解决。本文主要对线控转向技术中的变传动比技术和稳定性控制技术进行讨论，对转角跟踪部分使用PID 控制器自动调参进行定量研究。

因此，本文主要考虑汽车转向过程中的方向盘中心位置特性和速域特性进行变传动比模糊规则设计，实现模糊层面的图表查找法进行传动比的输出。搭建非线性2 自由度模型，建立动态横摆角速度差值滑模面进行反馈控制，并对趋近轨迹加以限制。通过动力学仿真软件搭建联合仿真模型，对多因素变传动比策略和改进后控制器的合理性进行测试验证。

1 系统模型搭建

1.1 车辆动力学建模

基于非线性2 自由度车辆模型，简化车辆侧向、横摆运动学方程为

式中，m为整车质量；Iz为横摆转动惯量；lf和lr分别为车辆质心到前后轴的间隔；Fy,f和Fy,r分别为前后轮胎的侧向力；γ为横摆角速度；vx和vy分别为车辆的纵向和侧向速度；δf为前轮转角；αf和αr分别为前后轮的侧偏角，本文cosδf≈1。

PACEJKA 轮胎模型[8]可用于计算轮胎的侧向力。忽略轮胎纵向力影响，通过经验参数值计算纯侧向滑移工况下的各项数值为

式中，μ为路面附着系数；a0=1.5，a1=0，a2=1 050，a3=1 200，a4=7，a5=0，a6=0.2。

前后轮胎的侧偏角定义如下：

式中，β为质心侧偏角。

1.2 线控转向系统建模

本文仅对线控转向执行总成进行系统建模，其中ECU 接受前轮转角信号后通过计算合理的前轮转角，输出对转向电机的进行位置控制，确保整个转向执行总成输出准确的前轮转角。定义功能模块包括转向器模块、驱动电机等。

齿轮齿条模块的动力学方程为

式中，Mr为转向齿条质量；xr为转向齿条位移；Br为转向齿条阻尼系数；F1和Fr分别为左前轮和右前轮施加在齿条两端的转向阻力；Kmd为转向齿条的扭转刚度；gsm为转向电机的减速比；θsm为转向电机转角；rp为转向小齿轮的分度圆半径。

转向执行电机电学平衡方程为

电机的电磁力矩与电流的关系为

式中，Tsm为转向执行电机转矩；Jsm为转向执行电机转动惯量；K2为转向执行电机电磁转矩系数；Bsm为转向执行电机阻尼系数；ism为转向执行电机电流。

简化转向电机模型可得

式中，Usm为转向电机电压；Rsm为转向电机电阻；Lsm为转向电机电感；Ksm为转向电机反电动势。

以上数学模型通过Simulink 搭建仿真模型后与CarSim 模型对比，验证非线性二自由度整车模型的正确性，便于后续研究，涉及的整车参数如表1 所示。

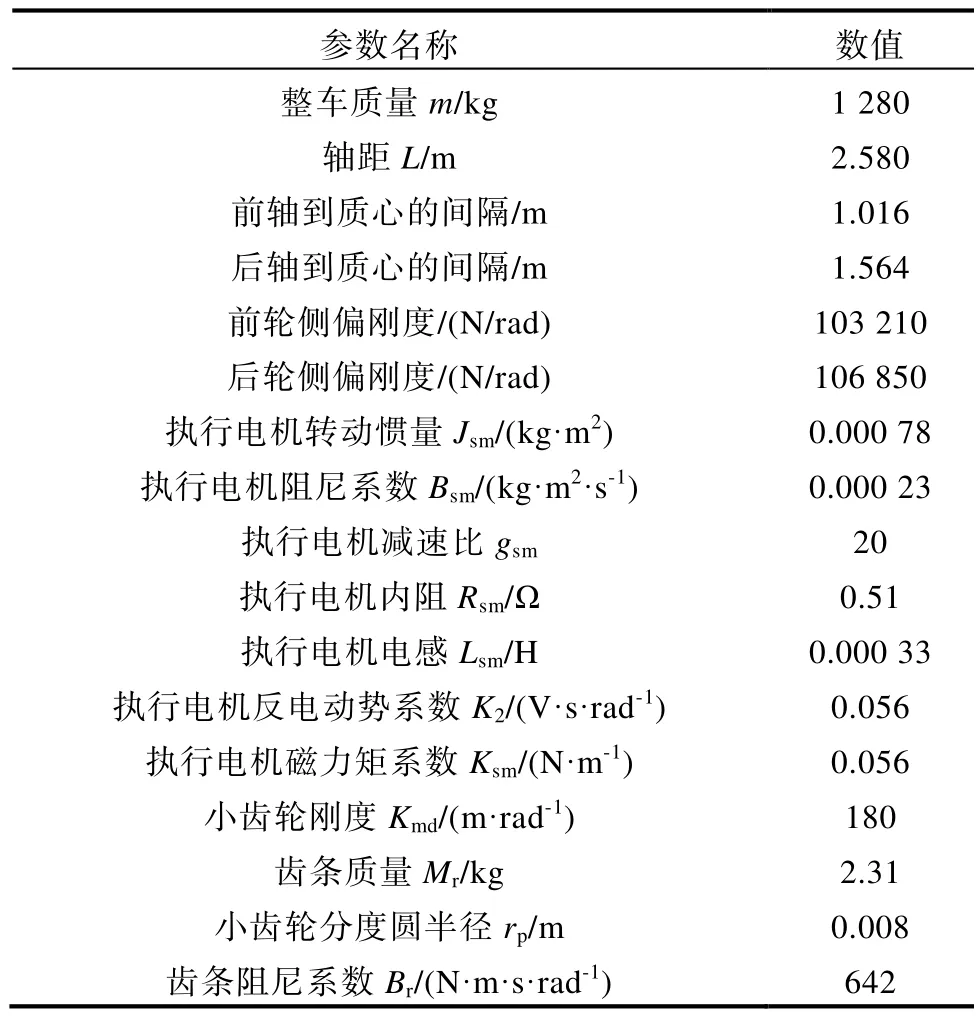
表1 整车参数

2 主动前轮转向滑模控制器

2.1 变传动比模糊策略

线控转向系统中，力学关系得以解耦，角传递特性得到改变。现有文献通过设计转向传动比改变车轮转角的映射关系，确保转向灵敏度保持不变，达到减轻驾驶员负担的目的。其中基于稳态增益的计算方法为通过计算固定增益进行数学推导，离线建立变传动比曲线或控制器模型。本文分析线控转向系统的指标需求、传动比设计的相关成因，最后综合考虑进行以下规则制定：

1）线控转向是乘用车底盘域控制的必要组成之一，在自动驾驶转向使能时，要求实现转向角分辨率不超过0.1°；转向角精度不超过1°；转向速度不超过540°/s，其中540°为机械转向方向盘单侧转角上限；角度环运行周期1 000 μs，输入为目标角度与实际轮胎（或方向盘）转速，输出目标转速，带宽30～50 Hz；保守助力保持在50%。此外要求功能安全等级为汽车安全完整性等级（Automotive Safety Integrity Level D, ASIL-D），且预期功能安全需要设计转向响应滞后导致的安全隐患问题。这一部分属于智能底盘域对线控转向的指标需求精度要求体现在实物产品开发中，本文不区分先进驾驶辅助系统（Advanced Driving Assistance System, ADAS）使能和自动转向使能，故不对此部分作深入讨论，只作ECU 的逻辑制定，对外围信号电路等不作要求。据文献调研本文可变传动比部分的设计可满足基础指标需求。

2）在速域特性中，车辆在低速行驶时，较小的转向传动比可以提高低速时的转向灵敏度；高速行驶时，较大的转向比则可以减小前轮转角的输出，改善行驶过程中的稳定性。文献[9]通过仿真分析得到，单纯地考虑一种增益是有失偏颇的，对前轮转向车辆来说，基于横摆角速度增益不变的可变传动比难以保证高速段的响应情况，对变传动比设计过程中低速段以横摆角速度增益为主，高速段以侧向加速度增益为主来增大全速域汽车行驶的稳定性。

3）在方向盘中心位置特性中，为了提高驾驶员转向操作的轻便性，在方向盘角度逐渐增大时需要逐渐减小转向传动比。在车辆行驶过程中，转向中心位置对转向比设计增量，同时为了防止因方向盘左右小幅度的摇晃等误操作造成的车辆行驶轨迹左右变化，随着车辆速度提高，方向盘中心位置处的转向比增量呈递减趋势，减少中间位置转向比增量对高速段的稳态增益的影响。同时方向盘转角的变化速率也会影响车辆横摆稳定性[10]，在高速情况下猛打方向盘时，可变传动比应随转向盘角度变化速率增大，本文通过实时监测方向盘角加速度θ˙，采取开关函数在车速大于100 km/h，方向盘角加速度大于1 时进行切换，可变传动比i随角加速度θ˙呈i=kθ˙变化，取k=17.3。

4）由于传动比的设置在不合理的情况下会带来一系列问题，下限过低会导致前轮转角达到转角极限值，上限过高会引起转向迟钝，在车辆换道、避撞及超车情况下产生严重影响。因此，根据研究中采取的车辆模型，设计车辆时速为0～120 km/h，参照国外已有的线控转向产品，设定模糊控制器内方向盘转角范围为-180°～180°，转向外侧最大车轮最大转角为30°，最小传动比选用6，最大传动比选用25。此外，路面附着系数也影响着可变传动比的取值，在曲线表现上为理想变传动比随着路面附着系数降低而提高[11]，本节主要采用模糊控制的设计，暂只讨论处于单一路况下的变传动比设计结果。

设置车速论域为{0，20，40，60，80，100，120}，方向盘转角论域为{-180，-120，-60，0，60，120，180}，转向传动比论域为{8，11，14，17，20，23，26}，模糊集均为{NB，NM，NS，ZO，PS，PM，PB}，基于三角形隶属度函数和重心法对模糊控制器输入输出进行处理。由此设计线控主动前轮转向车辆变传动比的模糊规则如表2 所示。

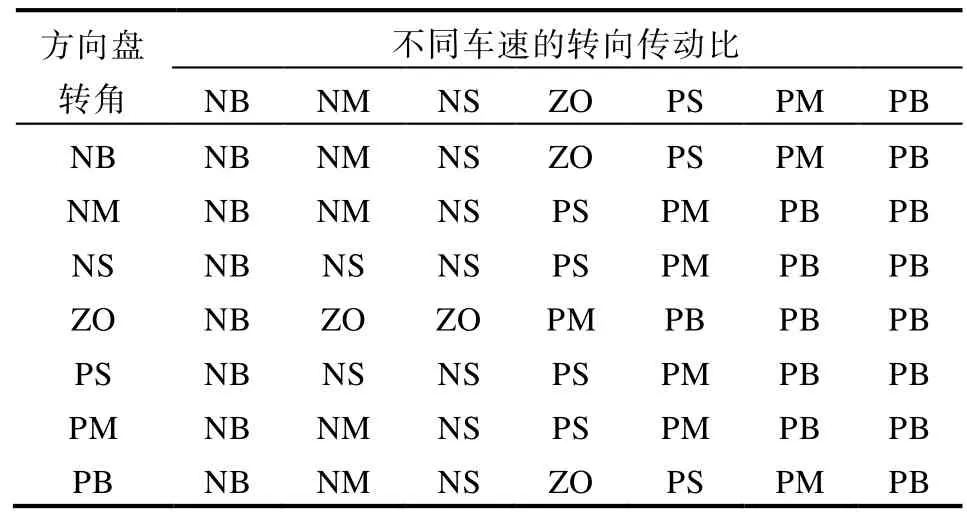
表2 主动前轮线控转向车辆变传动比的模糊规则

通过fuzzy control 设计可变传动比模糊策略生成map 图如图1 所示，车速为0～20 km/h 时，传动比约为6，此时比值小，能够使驾驶员在低速泊车等工况减小转向输入达到期望转向需求，提高转向灵敏度；车速为20～100 km/h 时，可变传动比与车速接近正比趋势，符合驾驶员操作习惯；车速为100～120 km/h 时，可变传动比为25，满足上述系统设计对稳定性的需求。

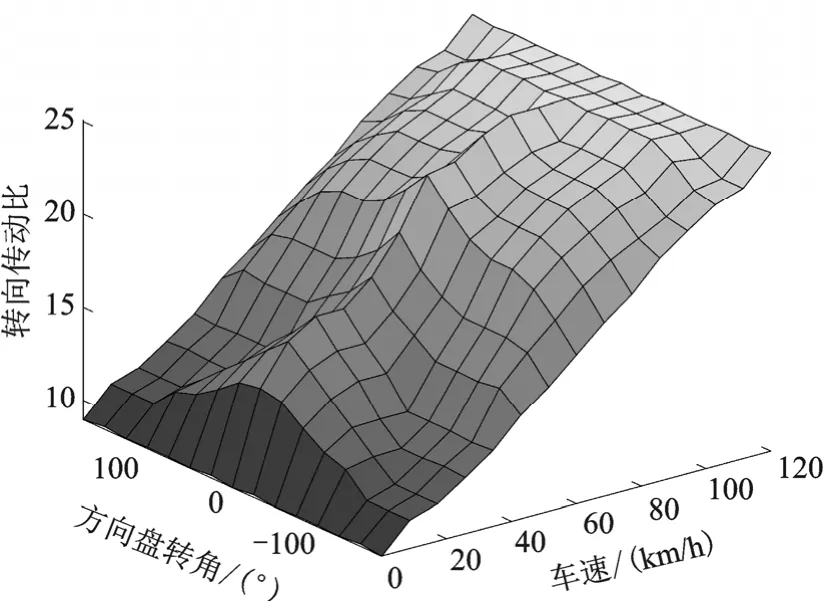
图1 线控转向传动比

2.2 改进滑模控制器

滑模控制能够应对复杂时变系统，应对参数变化带来的影响，保证系统良好的鲁棒性和自适应性，常被应用在汽车行驶稳定性的控制策略上。本节主要设计变指数滑模控制器对线控转向汽车的主动转向进行控制。

本文设计的滑模控制策略是对比实际横摆角速度γ与其理想值γd的差值，构建滑模面使实际横摆角速度跟随理想值的差值趋近滑模轨迹。设计基于非线性2 自由度模型的滑模控制器，设计最终决策转角输入为δf，为控制器补偿量Δδ和驾驶员的前馈输出δ*f之和。对于系统中的参考模型，采用非线性2 自由度模型，经过与2 自由度模型仿真对比发现前者与车辆动力学仿真模型的输出更为精确，能够更好地反映车辆的稳态响应情况。总体系统控制策略如图2 所示。

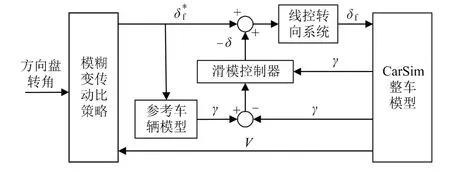
图2 系统控制逻辑图

则

滑模面为

根据2 自由度模型推导实际横摆角加速度为

其中

根据滑模控制的定义，系统在一定时间可收敛于切换面称为滑模控制的可达性，不同的设计轨迹将决定系统的收敛速度和效果。此时进一步确定趋近律，其中指数趋近律=-εsgn(s) -ks,ε＞0,k＞0 ，ε为系统趋近滑模面的速度，结合式（8）可知ε的设定决定系统到达滑模面的趋近速度及系统抖振大小。在传统指数趋近律中，通常将ε设计为常值，这意味着当ε较大时，系统趋近滑模面的速度较快，但抖振较大；当ε较小时，系统抖振较小，但趋近滑模面的速度较慢。针对以往传统指数趋近律存在的不足，这里改进的趋近律为

式中，f(s) = 1/[e|s|+ 1/|s|]。

由以上公式推导可得到系统的控制律为

3 仿真分析

3.1 角阶跃工况仿真分析

为了验证设计变传动比和改进滑模控制器的有效性，联合仿真通过在Simulink 中搭建转向系统模型，替代CarSim 整车模型（选取 C-Class Hatchback）中的转向系统，实现策略的验证。选取方向盘转角阶跃输入工况进行联合仿真分析，并与基于指数趋近率sat(s)饱和函数的控制器进行对比分析。设定试验初始条件车速为60 km/h，μ为0.85，在0～0.25 s 内方向盘角度输入从0 deg阶跃至90 deg，结果如图3 所示。由图3 可知，模糊变传动比相比固定传动比下的车辆横摆角速度和质心侧偏角明显降低，响应良好，满足了变传动比设计的功能和安全需求，操稳性和安全性得到提高，驾驶员的操作负担有效减轻。

图3 角阶跃工况响应仿真结果

设计滑模控制器A 为指数趋近律，引入饱和函数sat(s)通过动态切换状态来减小控制过程中滑模面附近的抖振现象，滑模控制器B 为本文改进后的变指数趋近律。在同样的方向盘角阶跃输入工况下进行了仿真验证分析，结果如图4 所示。改进控制器相比控制器A 性能优化明显，不仅可以有效跟随理想横摆角速的变化，而且在阶跃响应阶段控制器B 的超调量降低了9%，系统波动情况有所降低，有效提高了汽车行驶稳定性，控制器B 响应良好。

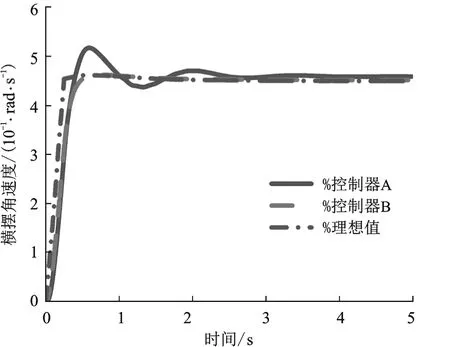
图4 控制器A/B 仿真结果

4 总结

通过利用车辆动力学模型仿真软件CarSim 和数学模型仿真软件Matlab/Simulink 搭建线控转向整车模型，对线控转向变传动比设计和稳定性层面的控制进行研究，主要研究内容如下：

1）基于两种固定稳态增益的特征、考虑对传动比的方向盘转角及车速两种影响因素，分析高速度段和低速段各自的影响侧重点，设计适用于主动前轮转向汽车的变角传动比模糊控制器，通过仿真验证相比固定传动比，能够降低车辆失稳状态指标，提高驾驶员转向轻便性，实现线控转向功能和安全需求。

2）搭建基于变指数趋近律的改进滑模控制器，跟踪车辆运行状态参数进行反馈控制，相比指数趋近律滑模控制器及饱和函数控制器能有效保证系统稳定性，减少系统抖振和超调量，改进反馈算法的效果得到明显优化。

对智能底盘车辆来讲，发展方向由驾驶辅助发展至自动驾驶，对转向系统的精度要求和功能安全要求逐渐完善，关键技术已成熟，后续将结合政策下的功能安全要求进行转向系统的修正。此外，由于模糊控制规则受限于设计者的经验知识，且模糊控制输出曲线的突变情况会造成电机冲突，影响工业应用可靠性和经济性。在后续的研究中也将进一步结合路面附着系数及其影响，分析突变路况的下车辆转向系统的响应特征，设计自然连续的可变传动比曲面，完善不同附着系数下状态切换条件或者生成混杂系统进行状态转换。同时，本文设计的反馈控制器验证仅限于仿真试验，下一步将搭建线控转向台架，结合驱动电机、speedgoat、传感器等设备，通过EtherCAT通信协议建立主从站及测试系统，进行控制策略的验证和改进。线控转向系统设计的最终目标是产品化，结合新型底盘集成控制，定义对应的模块接口，便于后续开发。