基于FTA-BN 的混合动力汽车故障诊断策略
2023-05-08万凌初牛礼民
万凌初 ,牛礼民,2 ,胡 超
(1.安徽工业大学 机械工程学院,安徽 马鞍山 243032;2.安徽工程大学 电气传动与控制安徽省重点实验室,安徽 芜湖 241000)
近年,新能源汽车市场规模快速扩大,带动了中国新能源汽车产品市场竞争力的快速提升,其中混合动力汽车(hybrid electric vehicle,HEV)在新能源市场占有重要地位。良好完整的汽车底盘系统可保证汽车的动力传输和转向的灵活,而底盘系统中只有离合器、发动机、电动机等各部件正常工作才能保证汽车具有良好的操稳性和平顺性,安全完成驾驶。因此,对汽车底盘系统部件进行故障诊断研究很有必要。
传统的机械故障诊断方法为人工判断法、简单仪表检测法,但人工判断和简单仪表检测准确度不高。随着计算机技术的快速发展,越来越多的学者研究采用故障模型、多智能体协调控制诊断等智能化的方法进行机械故障诊断。陈紫起等[1]将T-S 故障树与模糊理论相结合,提出了基于信心指数的专家调查法对柴油机进行故障诊断,但此方法推导过程复杂、运算量大,不符合用户诊断耗时短的需求;隋佳君等[2]结合Agent 技术的智能性和仿真模型的直观性,建立多Agent 故障传播模型,对润滑系统进行诊断,此方法能实现智能体系统的故障诊断,但Jade 编程环境复杂、难以工业应用;辛民等[3]通过设置最优权重机制,实现将专家系统用于车辆制动系统的故障识别与预警,但实际行驶过程中混合动力汽车的制动系统很少出现故障。综上可看出,目前研究多涉及汽车底盘单个部件的故障诊断,较少涉及汽车底盘系统中离合器、发动机、电动机、动力电池等多部件的融合故障诊断。
贝叶斯网络(Bayesian network,BN)是常用来解决非线性复杂系统不确定性推理的有效方法之一[4],同时能够结合多种渠道的信息进行判断推理,近年被越来越多地用于故障诊断领域。故障树诊断法将可能造成机构故障的原因逐级分解,绘制成如同树枝形状的图形进行表达[5]。基于此,通过收集HEV 底盘系统的故障现象,建立相应的故障树模型,提出基于FTA-BN 的底盘故障诊断策略,以期实现对HEV 底盘系统多部件的融合诊断。
1 基于FTA-BN 故障诊断系统的构建
HEV 底盘故障诊断系统的总体设计如图1,系统由故障库、数据表、推理机和人机交互界面等组成,通过信号采集设备搜集车辆底盘故障信号,将其输入诊断系统基于FTA-BN 计算出事件可信度,通过显示页面观察相应的诊断结果。以VB 语言作为程序开发语言,利用SQL Server 构建HEV 底盘故障的数据库,通过相应的控件实现对故障库的快速访问及故障的采集判断,完成对车辆底盘集成系统故障的智能诊断。
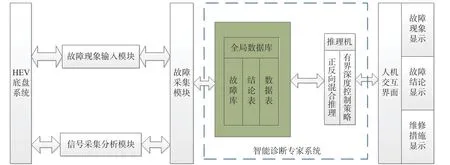
图1 故障诊断系统总体设计Fig.1 Overall design of fault diagnosis system
1.1 故障库的建立
文中主要构建离合器故障、发动机故障、电动机故障、动力电池故障等4 种故障树模型。故障树模型根据专家经验建立不易更改,而贝叶斯网络在信息处理方面具有较好的自学习能力[6]。故障树模型和贝叶斯网络具有相似的拓扑结构,考虑将故障树模型中的事件映射为贝叶斯网络,这样可有效融合专家的先验知识与数据驱动的方法,准确表达推理决策过程中的不确定性[7]。
贝叶斯网络由条件概率表和有向无环图组成,按照文献[8-9]中的转换方法,将故障树模型中的逻辑门关系与贝叶斯网络模型节点和条件概率进行转换处理。故障树的逻辑关系由与门和或门组成,故障事件中分成正常和故障状态,对应的贝叶斯网络中节点变量分别取0 和1,表示正常和故障状态。故障树逻辑门关系与贝叶斯网络节点的转换关系如图2。

图2 故障与非门和贝叶斯网络的转换Fig.2 Transformation of fault tree logic gate and bayesian network
通过3 条基本规则,可将故障树模型转换成贝叶斯网络模型:故障树模型中各底事件、中间事件、顶事件要与贝叶斯网络中的各节点对应;若故障树中底事件有多个相同,则在贝叶斯网络中将相同的底事件设定为一个节点;故障树模型中的事件与贝叶斯网络中的节点存在相互映射关系[10]。故障树与贝叶斯网络的转换流程如图3。
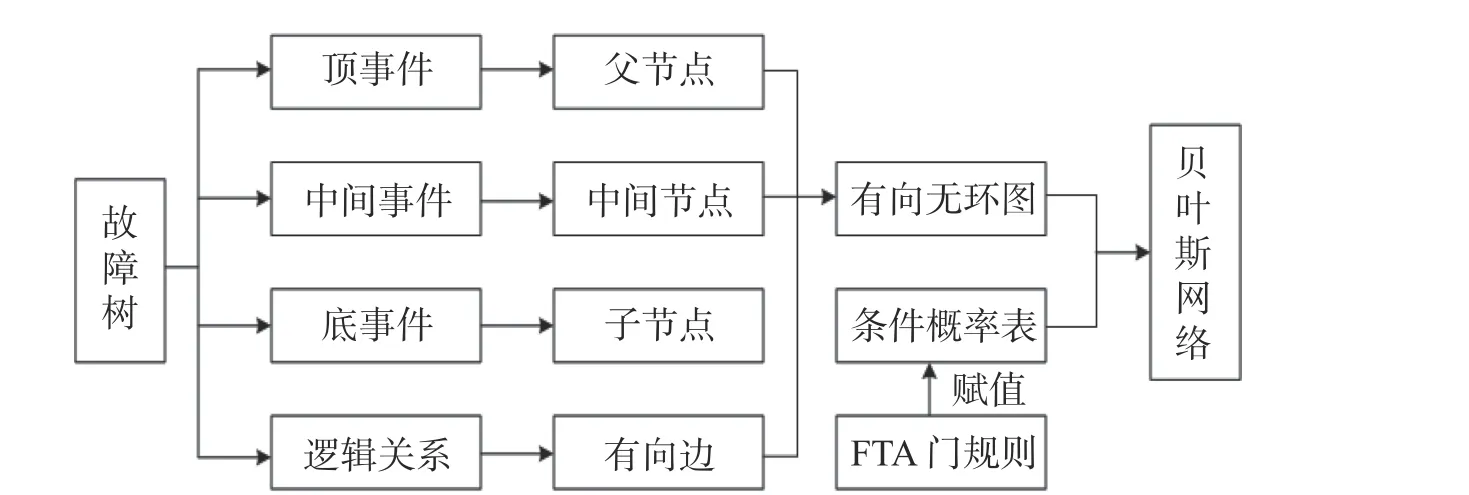
图3 故障树与贝叶斯网络转换Fig.3 Transformation of fault tree and Bayesian network
建立故障树的过程也是知识获取的过程,把构成故障树的顶事件、中间事件存入故障库,再把底事件即故障结论存入数据库,通过主键和外键的关系把各级故障树联系起来,完成故障库的建立[11]。此外通过查阅相关文献资料、询问有关技术专家和工人的经验,将这些经验进行归纳总结录入故障库。文中利用SQL Server 数据库管理系统创建HEV 底盘集成系统故障库,如图4。
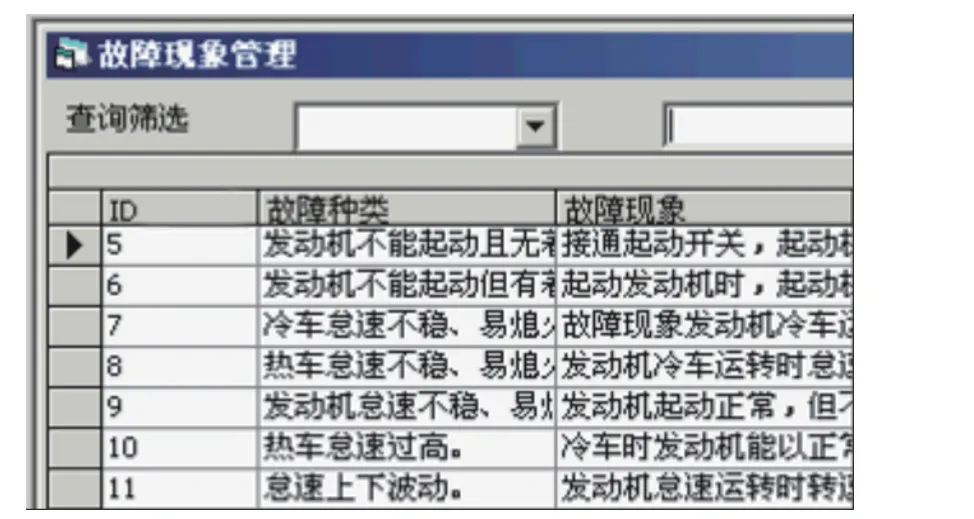
图4 故障库Fig.4 Fault database
1.2 数据表的创立
数据库中的繁杂信息需有适当的存储形式,使之在数据库中便于管理和调用。该系统将重要信息存放在数据表中,如表1,其中包括用户信息、故障记录、诊断次数等关键信息,为防止数据混乱,表中的任何一条记录都是唯一确定的。
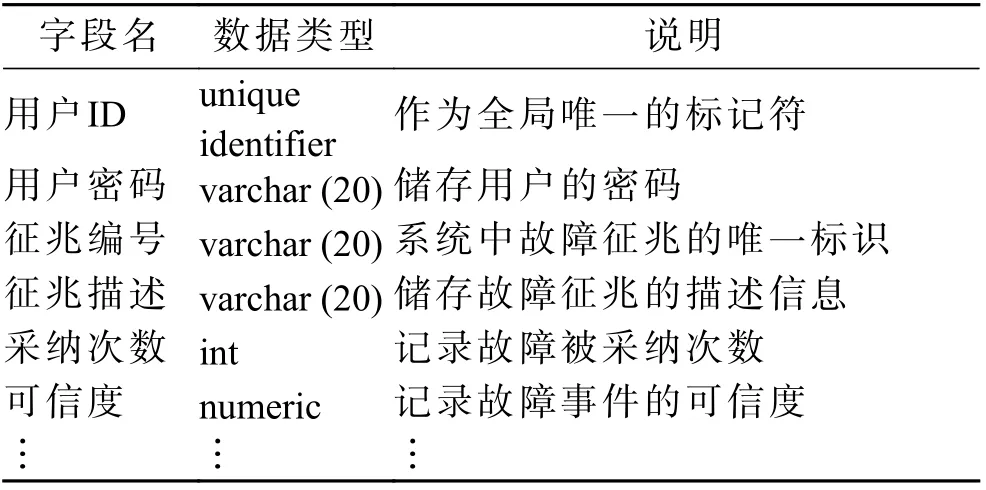
表1 数据表Tab.1 Date sheet
1.3 搜索方法的设计
搜索方法可分为深度优先和广度优先[12]。文中采用有界深度优先的搜索方法,从开始节点出发向子节点的方向逐级向下纵深搜索,并判断这些节点是否为目标点,如果到达深度阈值还未发现目标节点,返回上层父节点的其他子节点进行搜索,循环过程中找到目标节点。用户通过交互界面输入故障事件,系统以此为依据实现节点指针的位置变换,不断搜索子节点得出故障结论,用户可根据界面显示的故障结论采取相应的处理措施,故障诊断系统界面如图5。
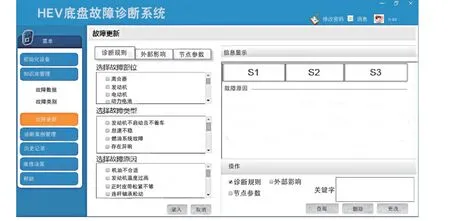
图5 诊断系统界面Fig.5 Diagnostic system page
2 基于FTA-BN 故障诊断系统的节点分析
2.1 基于全概率的故障事件
故障树模型分析分为定性和定量分析,用户输入故障征兆逐级推理出底事件,得到引起顶事件发生的最小割集,通过相应规则合理过滤与故障无关的故障树节点,节省诊断时间。采用下行法自上而下的顺序搜寻故障树,推理逻辑中的“与门”和“或门”会增大割集的数目,从故障顶事件开始依次把事件替换成下一级事件,最终简化得到系统的最小割集[13]。以电动机故障树模型为例,通过故障实例构建电动机故障顶事件,中间事件主要包括通电不启动、异常振动、空负载电流不平衡、电机异响等4 种,如图6。
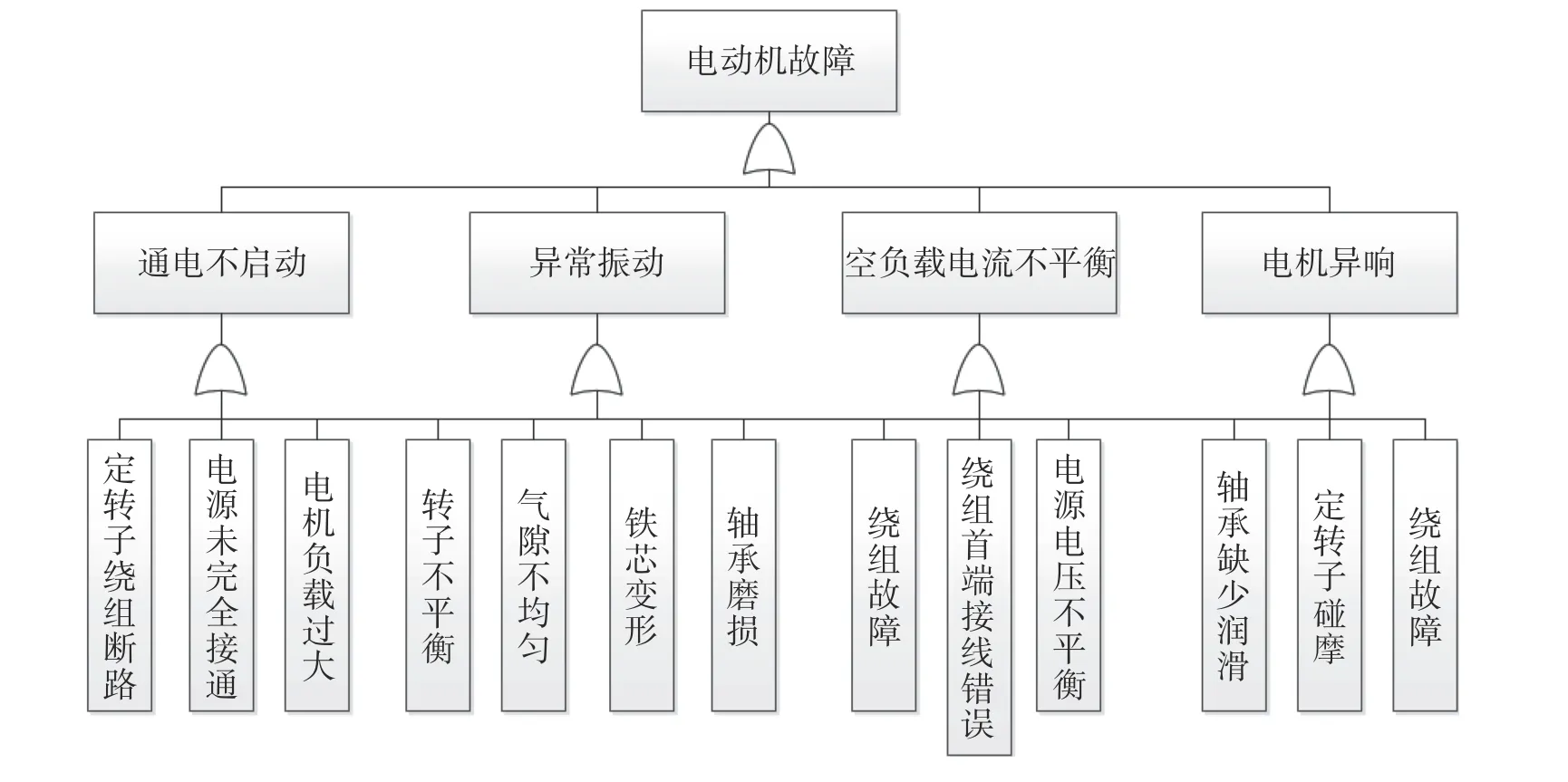
图6 电动机故障树Fig.6 Motor fault tree
系统中故障树大部分是或的关系,图6 中所示的故障树有13 个割集x1,x2,···,x13,其中存在子集C={x1,x2,x3,x4}, 且子集C∈ {x1,x2,···,x13},当集合C= (x1=x2=x3=x4=1)时 ,P(T)=1。这时顶事件T必然会发生,称子集C是顶事件T的一个割集,去掉割集中的任一底事件,都可引起顶事件T的发生,称该集合为最小割集。
定量分析是研究故障模型中所有导致顶事件发生的最小割集,计算确定相应顶事件的发生概率且求出底事件的相关重要度[14]。重要度指当故障树中各节点对应的故障事件、集合及最小割集发生时,引起顶事件发生的可能性,一般重要度包括概率重要度和关键重要度。
假设每个底事件是相互独立同时具有故障和正常的2 种状态,形成条件概率(A=i|B=j)来描述不同事件之间的概率关系。假设故障顶事件T发生,最小割集中事件相互独立且并不相容,可计算出顶事件发生的概率P(T):
式中:xi为割集;qi为底 事件发生的概率。底事件的概率重要度I1(i)为
通过降低相应事件的概率重要度就能降低故障顶事件的发生概率。通过故障树顶事件的发生概率可得到底事件i发生概率的变化率与引起顶事件发生概率变化率的比值,该值称为事件关键重要度或临界重要度,底事件的关键重要度I2(i)为
通过关键重要度可从敏感度和概率双重角度反映该事件对顶事件的影响。底事件的关键重要度与概率重要度的关系为
式中g为比例因子。
2.2 基于FTA-BN 的节点可信度
建立以故障征兆为顶事件、故障原因为底事件的故障树模型,结合贝叶斯网络求得在父节点发生条件下故障子节点的概率。求出的概率代表故障节点发生的优先级,可作为相应事件可信度,可较好地对系统发生故障时进行判定并得出可靠结论。
以图7 所示的三单元串并联简化贝叶斯网络模型为例介绍节点概率计算过程,假定T为电池故障,A为温度过高,最小割集x1,x2,x3分别为电池SOC 值低、风扇未启动、温度传感器损坏。
当系统为一般可靠性时,将2 个子节点看作互斥事件,可看出三单元有23-1=7 种故障状态,每个状态之间互斥,根据全概率理论结合贝叶斯网络可算出该父节点发生时子节点的发生概率:
式中:P1,P2,P3分别为子节点在某时间的发生概率;P(x1/T),P(x2/T),P(x3/T)为父节点T发生的情况下,子节点x1,x2,x3分别发生的概率,以此作为导致故障发生的可信度。
继续推导n个故障节点导致故障结论的可信度,引入2 个变量θ 和σ,表示节点的状态和此模式条件下的系统状态,0 表示正常状态,1 表示故障状态[15]。
式中:θk为 第k个故障状态下父节点T的状态;σk为第k个故障状态下第m个子节点的状态。由此可推导出在父节点T发生的情况下,任一故障节点发生的概率,并以此作为每个故障现象的可信度;

3 基于FTA-BN 故障系统的诊断
3.1 故障诊断流程
利用安装在车身的传感器监测得到的油箱压力、节气门开度、冷却剂温度等历史数据并结合相关领域的专家知识和经验完成故障树模型的建立,通过分析故障树的逻辑关系,找出网络节点的因果关系,结合基本规则完成面向对象的贝叶斯网络的建立[16-17]。在线诊断时,将故障现象输入面向对象的贝叶斯网络进行定量推理分析,如车速压力等将被作为参数输入故障征兆节点,计算出相应故障节点的可信度。在诊断系统中引入贝叶斯网络模型进行判断,排除车辆非线性系统的不确定性干扰。诊断策略实现步骤如下:
1) 用户在系统页面输入故障现象;
2) 系统根据输入的现象匹配合适的故障树,并搜索相应故障库中的结论;
3) 根据规则库寻找相应的故障节点;
4) 基于FTA-BN 计算网络中节点的可信度;
5)根据可信度输出故障源排序及故障状态信息。
基于贝叶斯网络系统诊断流程图如图8。
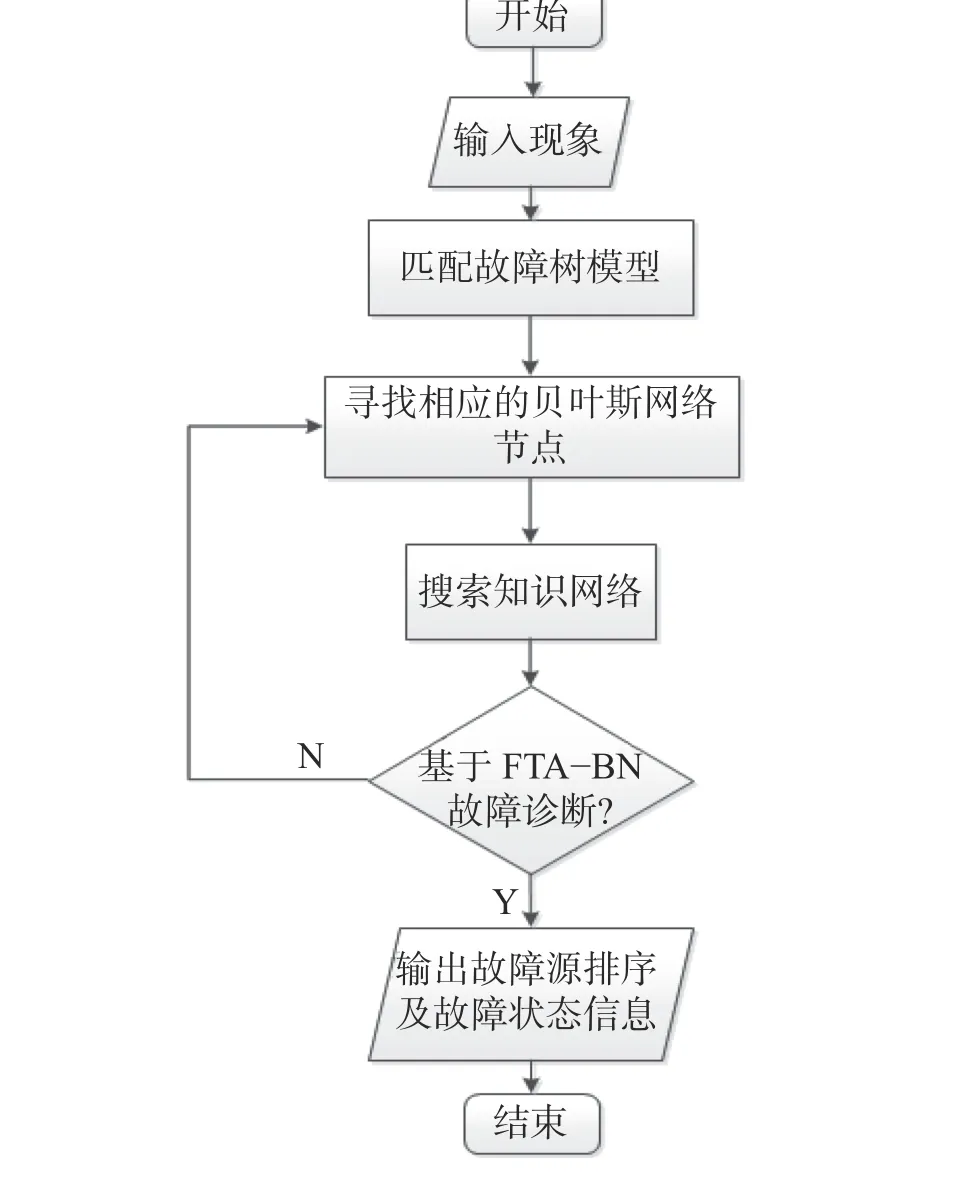
图8 基于贝叶斯网络诊断流程图Fig.8 Flowchart of diagnosis based on Bayesian network
求出的故障原因可信度是衡量该项原因对故障征兆影响的可信任程度,通过对节点的可信度排序,由高到低设置故障节点,使诊断系统快速定位到故障部位,优化算力,提高诊断效率。
3.2 故障诊断实例
使用连接线ES581 将电脑连接到车辆的电子控制单元(electronic control unit,ECU)收集车辆状态信息,将信息输入图1 所示的底盘故障诊断系统,通过提出的FTA-BN 策略计算事件的可信度,得出车辆的故障结论,给出相应维修建议。
通过BorgWarner 燃油动力系统公司内部试验场实车故障系统采集车辆数字信号和参数,结果如图9。SOAKTIME 为进气时间259 s ,VAMBTEMP 为环境温度24 ℃,FLTFLVLP 为油位信号,VIATSU 为进气温度24 ℃,VCOOLTSU 为冷却剂温度28 ℃,VKPH 为车速20 km/h,PURGEDC 为碳罐电磁阀开度随汽车发动开始增压,FLTDTVAC 为油箱压力等。基于提出的FTA-BN 策略对实车底盘系统进行检测,结果如图10。由图10 可看出:车辆发动机在行驶过程中存在异常,系统根据采集的数字信号计算出事件的可信度,可信度大于0.5 的故障结论为皮带松紧不够;诊断结论为调节相应皮带轮松紧度,排除车辆故障。
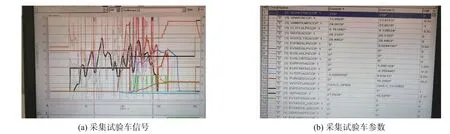
图9 试验车辆的采集数据Fig.9 Acquisition data of test vehicle
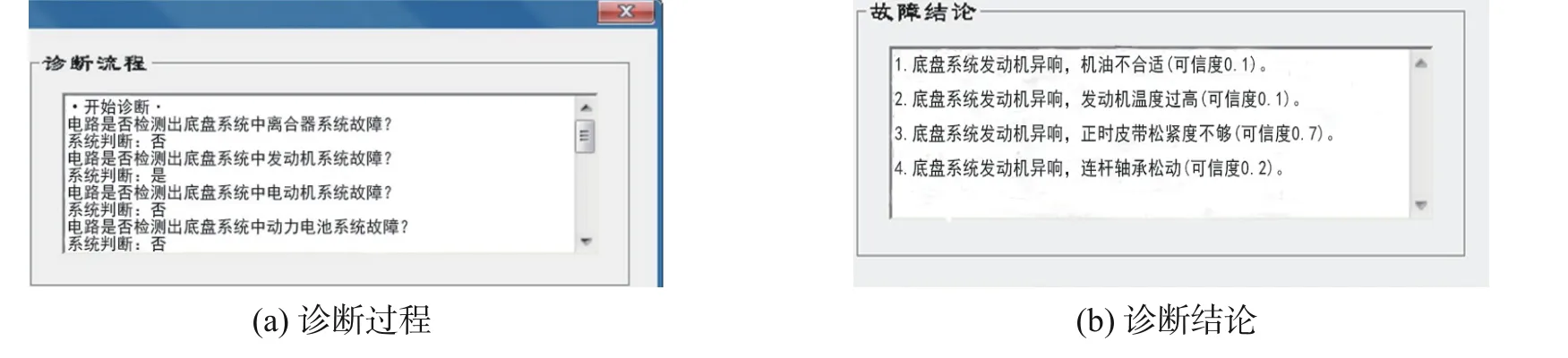
图10 诊断系统定位的故障Fig.10 Fault located by the diagnosis systemt
在BorgWarner 公司整车标定部门工程师的帮助下,利用采集的数据对设计的故障诊断系统进行验证,并与维修部门的人工经验判断结果进行对比。限于时间和成本的因素,进行小样本试验,共进行80 次,分成4 组,每组20 次,分别利用设计的故障系统诊断和人工各判断10 次,统计每次试验的故障情况,结果如图11(a)。由图11(a)可看出:依据FTA-BN 判断,故障事件为离合器、发动机、电动机及动力电池等故障,次数最高的故障事件为离合器故障、其次为发动机故障,符合混合动力汽车轻型车测试的实际道路运行状况中底盘中的离合器和发动机易发生故障的情况;依据人工经验判断,故障事件也均为离合器、发动机、电动机及动力电池等故障,次数最高的故障事件也为离合器故障,与FTA-BN 诊断结果一致,只是故障次数与FTA-BN 诊断结果若有差异,这主要是因为人为判断存在偶然性。将试验结果输入MATLAB 进行绘图,得出故障诊断准确度,结果如图11(b)。由图11(b)可看出:基于FTA-BN 故障诊断得出的准确度分别为0.9,0.8,0.9,0.8,平均故障诊断准确率为0.850;人工经验法得出的准确度分别为0.7,0.6,0.7,0.7,平均诊断准确率为0.675。提出的FTA-BN 策略故障诊断准确度大大高于人工经验,且能对混合汽车底盘系统进行融合诊断。
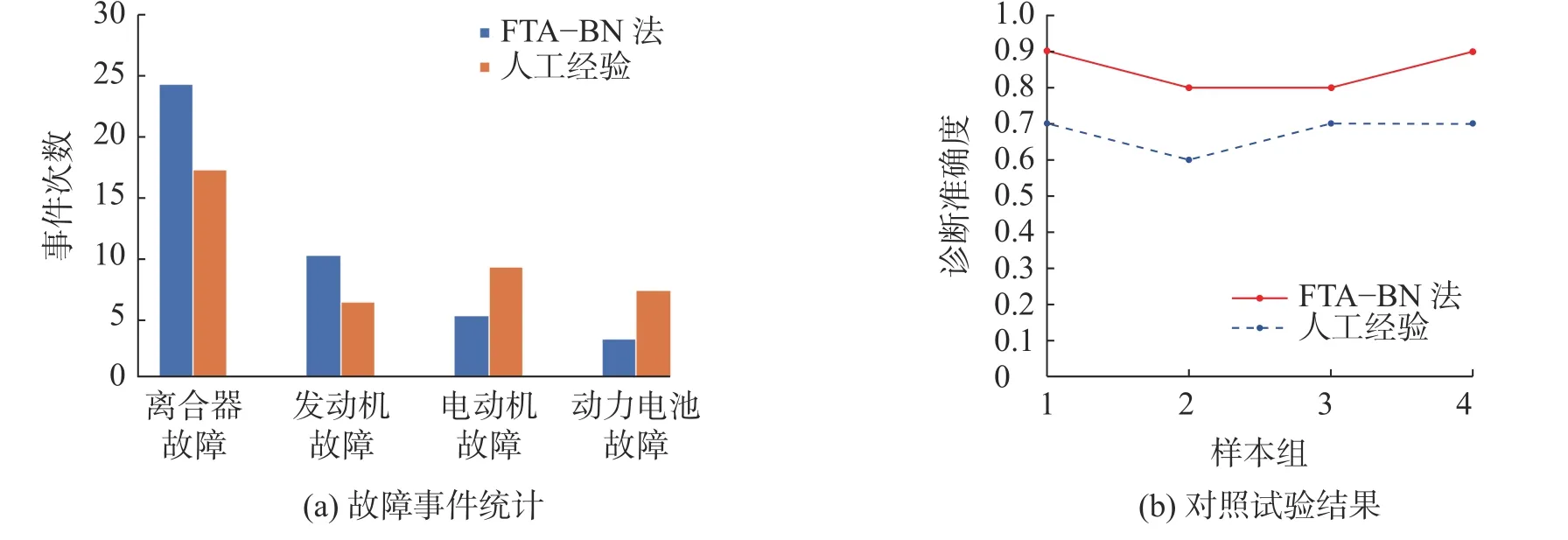
图11 故障诊断对照试验结果Fig.11 Fault diagnosis control test results
4 结 论
通过故障搜集,构建HEV 底盘系统故障树模型,再根据基本规则转化为网络节点,提出采用FTA-BN策略计算故障节点的可信度,根据节点概率输出相应的故障状态信息。样本对照试验结果表明:采用提出的FTA-BN 策略能对混合汽车底盘系统进行融合诊断,故障诊断的准确率为0.850,优于人工经验诊断的准确率(0.675)。进一步的研究重点是对代表故障的相关参数进行提取并输入神经网络进行训练,利用智能仿生算法和模式识别进行故障诊断,进一步提升诊断的准确率。
