J307 轮箍径-轴向轧制变形分析

黄林松 ，程明忠 ，黄孝卿 ，沈晓辉

(1.宝武集团 马钢轨交材料科技有限公司, 安徽 马鞍山 243010；2.安徽工业大学 冶金工程学院, 安徽马鞍山243032)

轮箍是组合式机车轮的重要部件[1]。轮箍作为一种典型的异形断面环件，过去采用粗轧+精轧两步轧制工艺，并在精轧中采用封闭孔型轧制成形[2]。为简化生产工序提高效率，在大型环件轧机上采用开口式孔型进行轮箍的单工步连续轧制成形，但开口孔型轧制的变形特点与闭式孔型显著不同。尽管环件轧制的基本理论得到一定发展[3]，但环件轧制时接触面会产生复杂的滑动现象[4-5]，金属变形解析难度较大，对其变形及工艺参数优化的研究多依赖有限元仿真分析[6-7]。环件径-轴向轧制仿真的关键问题是模型中辊系运动的正确控制，针对轧辊运动轨迹的控制，学者们提出了多种闭环控制算法。Deng 等[8]建立环件刚度条件的数学模型并提出一种导向辊的控制方法；郭良刚等[9]提出一种基于目标驱动的环件轧制闭环控制算法，实现轧辊运动轨迹的控制，并用于钛合金环件的控温轧制[10]；Peng[11]基于环件外表面12 个节点的位置跟踪计算环件外径变化，提出导向辊和锥辊运动的自适应控制算法。以上学者提出的环件轧制辊系运动控制算法均是针对具体的工艺条件，不能直接用于轮箍的径-轴向轧制仿真。

轮箍是一种断面形状复杂的环形件，相较于矩形截面环件，金属变形及工艺参数对异形截面环件轧制的影响更复杂。对于部分异形截面环件如锥形环件和内台阶环件[12-13]、L 型截面环件[14]、T 形环件[15]轧制过程的研究取得了一定成果，但对于轮箍这种带有外凸缘异形截面环件轧制过程的金属变形规律还有待进一步研究。Shen 等[16]、肖锋等[17]、丁彬花等[18]基于Marc/Superform 软件对车轮的轧制过程进行了有限元仿真，分析了车轮轧制过程的金属变形规律，为实现轮箍轧制的仿真提供了一定参考。对于轮箍轧制，横截面沿轴向呈非对称性，轧制过程金属的流动和轧制稳定性条件复杂。鉴于此，提出基于轮箍轧制过程实时外径变化的辊系运动自适用控制策略，建立轮箍轧制仿真模型，分析轮箍轧制过程的金属变形规律，为轮箍轧制工艺优化提供理论参考。

1 轮箍轧制模型建立

轮箍径-轴向轧制工艺如图1 所示：轧制过程中主辊和上锥辊旋转驱动轧件旋转；芯辊向主辊方向进给实现壁厚减薄，上锥辊压下实现高度减小；随环件外径的长大，锥辊向右侧平移，上下锥辊的锥心尽量保持对准环件的中心；左右抱辊向外侧移动，对环件保持一定的压力并使环件稳定旋转；主辊和芯辊间的辊缝构成径向变形区，上下锥辊间的辊缝构成轴向变形区；环件金属在径向、轴向2 个变形区内连续反复变形，实现径-轴向轧制。主辊上刻有孔槽，实现轮缘的成形。轮箍轧制过程是典型的三维非对称连续渐进变形过程，需建立完整的3D 模型才能对其进行仿真分析，辊系运动的准确描述是模型的关键。

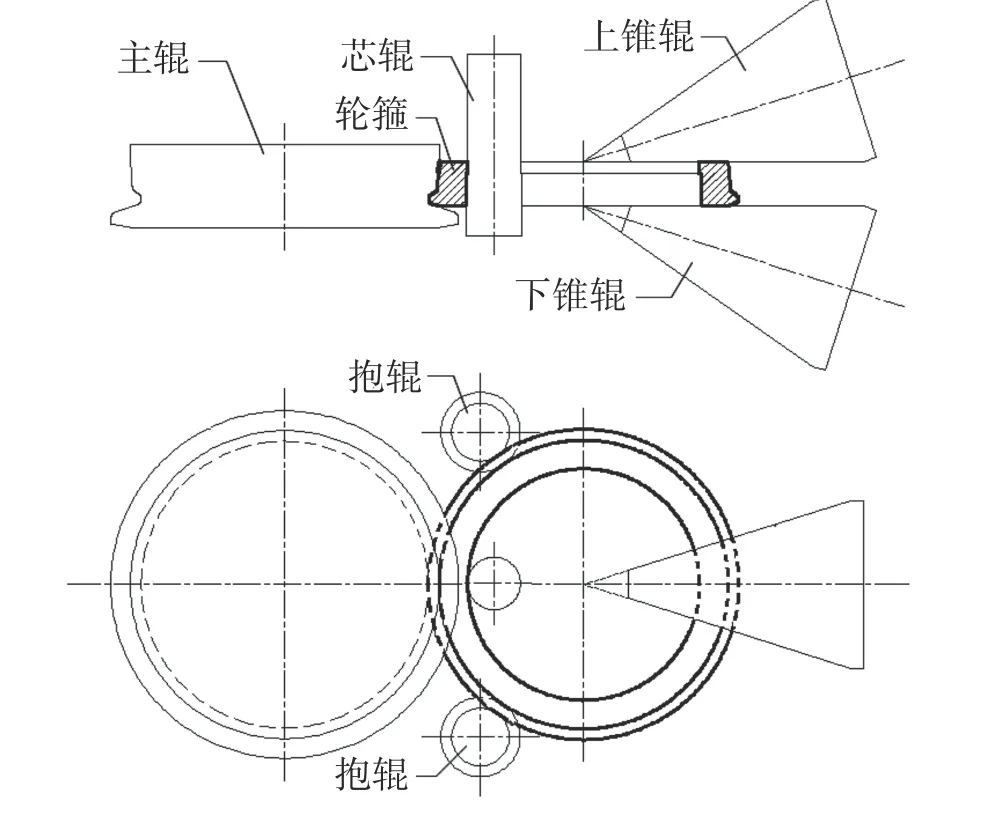
图1 轮箍径-轴向轧制工艺示意图Fig.1 Schematic diagram of railway tyre radial -axial rolling process

基于Marc/SuperForm 有限元分析软件，通过编写子程序实现芯辊、抱辊及锥辊的自适应控制运动，对J307 轮箍轧制过程进行模拟。建立的轮箍轧制有限元模型如图2，轧制粗制轮箍的目标外径(1 085±3)mm、目标高度(151±2)mm。

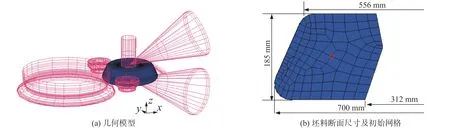
图2 轮箍轧制有限元模型Fig.2 Finite element model of railway tyre rolling

有限元模型中，轧件为变形体，工具为刚性体，轧件材料参数读取材料库中的C60 钢。设置坯料初始温度1 100 ℃，轧制过程中环件对周围的换热系数0.05 N/(s·mm·K)，辊面温度300 ℃，轧辊与轧件的接触传热系数15 N/(s·mm·K)，摩擦系数0.4，主辊转速2.45 rad/s。除主辊转速，其他轧辊或工具运动速度的设定依赖于环件实时外径的大小。芯辊进给速度和上锥辊辊缝高度的设定曲线如图3。外径增至1 069 mm 时，芯辊进给速度降至0.1 mm/s。锥辊辊缝高度随外径增加基本呈线性减小趋势，外径增至1 063 mm 时，锥辊辊缝高度达到目标值。轮箍轧制过程中金属变形量较大，尤其是轮缘部位网格发生严重畸变，为保证模拟的顺利进行，需进行网格自动重划分设置。加载时间步长0.004 17 s，总加载时间在子程序中通过判断外径目标尺寸再自由轧制2 圈来确定。

图3 芯辊进给速度及锥辊辊缝高度设定曲线Fig.3 Setting curves of core roller feeding speed and cone roller gap height

轧制过程中，随环件外径的长大环件中心位置发生变化，锥辊根据外径变化做平移运动，以保证锥心对准环件中心。锥辊旋转速度在轧制过程中也是变化的，需考虑径向、轴向变形区线速度的匹配及左右抱辊的受力情况对其进行动态调整。根据左右受力情况实时对称调整左右抱辊，保证轧制过程环件不发生左右偏移。芯辊进给速度、锥辊的旋转速度及平移速度和上锥辊的压下速度、左右抱辊的移动速度取决于模拟过程中环件外径的长大情况，因此提出基于轮箍轧制过程实时外径变化的辊系运动自适用控制策略。通过设置一个弹簧控制的测量辊实时测量轧件外径，通过编写子程序控制各工具的自适应运动。子程序结构如图4。

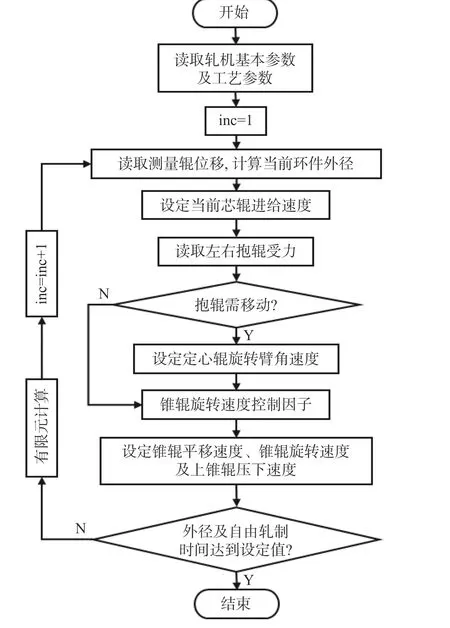
图4 辊系运动设定的子程序结构Fig.4 Subroutine structure of roller system motion setting

图5 为模拟过程中由子程序计算得出的锥辊旋转角速度变化情况。轧制过程中随轧件外径的增大，轴向变形区接触部位对应的锥辊外径增加，锥辊旋转角速度基本呈逐渐降低趋势。环件径-轴向轧制模型中，锥辊运动的描述是建模的难点之一，文中提出的算法可解决模型中锥辊转速设定问题。

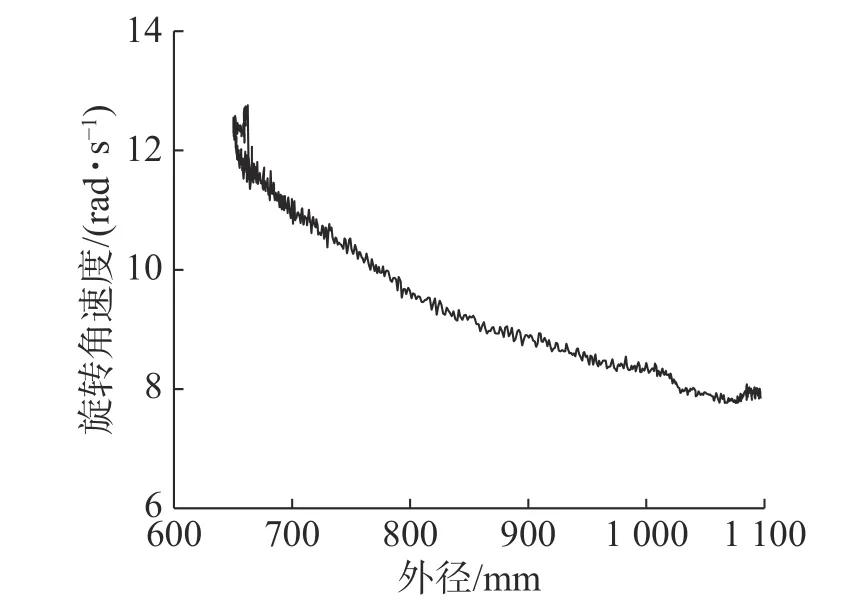
图5 轧制过程锥辊的角速度Fig.5 Rotation speed of cone roller during rolling

2 仿真结果分析

2.1 轮箍轧制过程的尺寸变化

模型加载时长为34 s，轮箍轧制16 圈，最终外径为1 092.0 mm，在目标尺寸的公差范围内。图6为轧制过程环件外径、壁厚的模拟值与试轧实测值。由图可6 看出：轧制15 s 后环件的外径模拟值与实测值基本一致，10 s 前，两者差异的主要原因是环件轧机实际记录的外径≥设置的初始外径(试轧初始外径为700.0 mm)，轧制初始阶段外径(踏面处)的减小过程在输出数据中没有体现；径向变形区的厚度模拟值与实测值相差不到2%。考虑到轧制初始阶段输出的外径不能反映外径减小情况，轮缘基本成形后扩径阶段的外径模拟值与实测值具有较高程度的一致性，认为轮箍轧制仿真模型具有较高的可靠性。

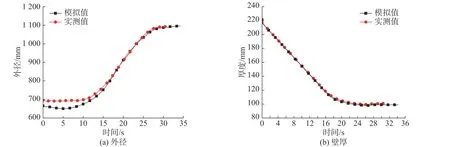
图6 轧制过程环件外径和壁厚模拟值与实测值的比较Fig.6 Comparison between simulation and measured values of the outer diameter and thickness of ring during rolling

由于环件外径的不断变化，轮箍轧制过程每圈旋转所需时间不同，第三圈时外径最小，所需时间也最短，为1.63 s；此后，每圈时间逐渐增多，第16 圈所需时间增至2.63 s。图7(a)为模拟所得环件外径与轧制圈数的关系。由图7(a)可看出：前3 圈轧制中，环件外径由666.0 mm 减至650.4 mm，主辊与环件外径面、芯辊与环件内径面逐渐贴合，变形集中在环件的内外径面；第3 圈后外径长大速度呈非线性变化，第9～13 圈外径增加量较大，第10 圈外径增量最大、约78 mm，实际轧制过程中需关注此阶段的外径增加量对轧制稳定性的影响，可适当减小芯辊进给速度；最后2 圈外径增量很小，仅约5 mm。图7(b)为模拟过程轴向变形区高度与轧制圈数的关系。由图7(b)可看出：轴向变形区高度的变化主要发生在第8～13 圈；第10，11 圈上锥辊有较大压下量，约9 mm。

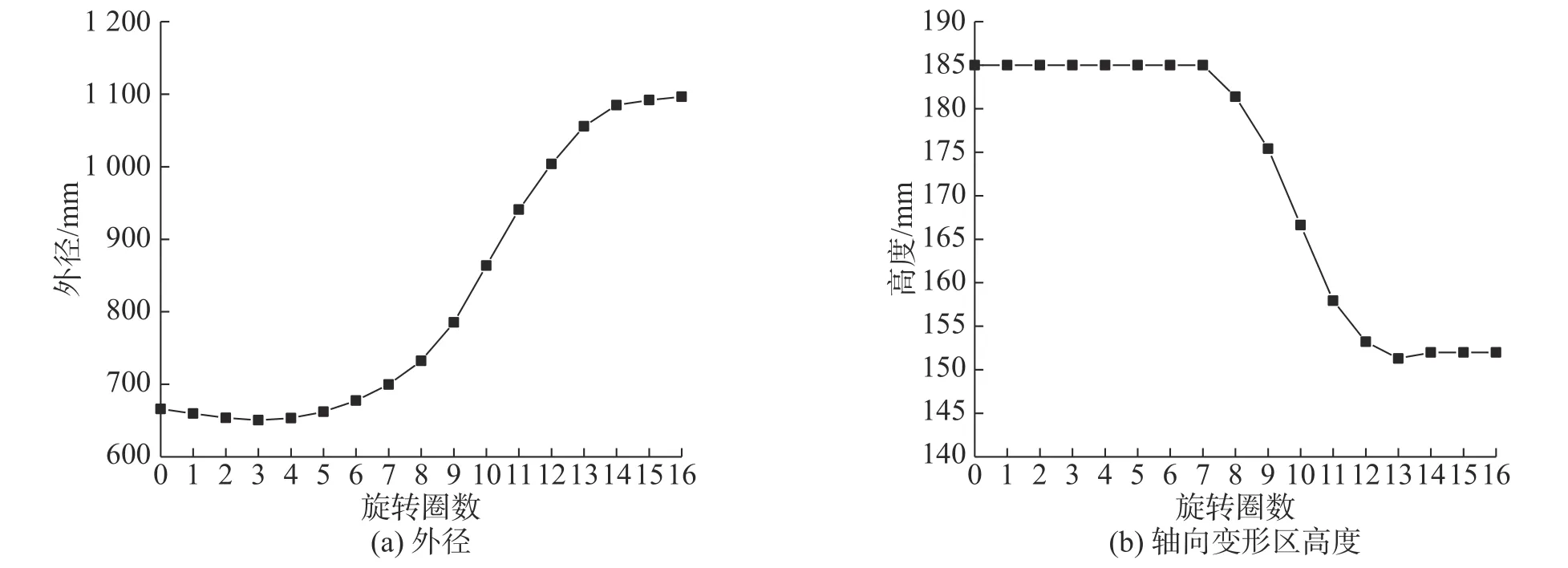
图7 轧制过程环件外径和轴向变形区高度Fig.7 Ring outer diameter and axial deformation zone height during rolling

径-轴向轧制时，径向变形区径向压下，轴向高度增加(轴向宽展)；轴向变形区高度压下，径向厚度也会相应增加(径向宽展)。图8 为轧制过程中某一截面高度的变化情况(图中每个竖格线间隔为轧制1 圈)。由图8 可看出：前6 圈轧制过程中，由于外径变化较小，锥辊没有有效压下，截面高度变化很小，第6 圈后截面高度呈明显矩形波动式变化；轧制至第10 圈时，径向变形区环件截面高度增加(轴向宽展量) 最大、达3.8 mm，轴向变形区高度压下量达11.5 mm；第11 圈时，轴向变形区环件截面高度压下达最大、达13.4 mm；第9～12 圈轧制过程中，径向、轴向变形区的轧制压下量较大，这与图7(a)中显示的此阶段扩径量较大对应；轧制末期，截面经2 个变形区时，高度仍有一定程度的变化，表明轧制结束时环件沿周向高度分布并不均匀，周向高度波动量约2.6 mm。

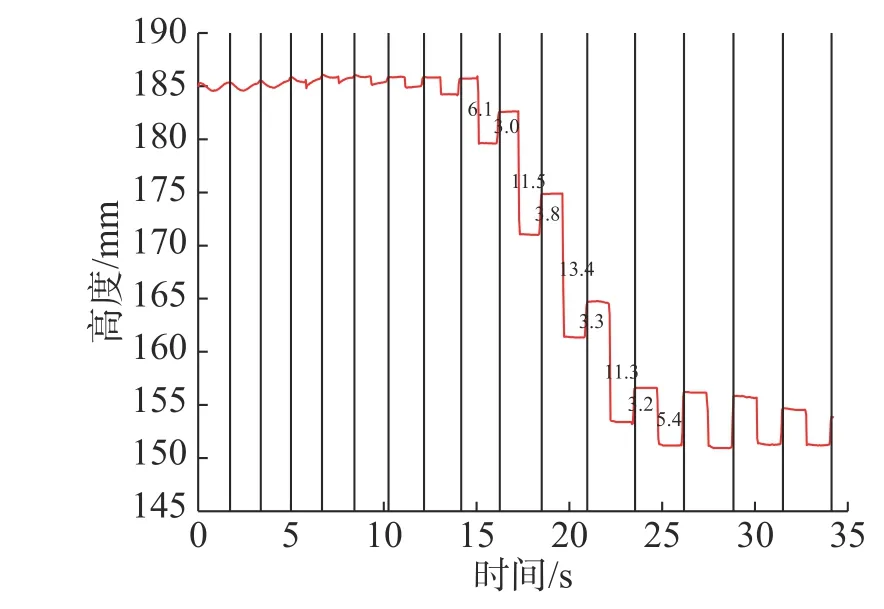
图8 轧制过程环件截面高度的变化Fig.8 Variation of ring section height during rolling

2.2 轮箍轧制过程的变形

轮箍轧制过程中变形分布很不均匀，内径面和外径面附近的变形显著大于截面心部。图9 为轧制不同时刻轧件的等效塑性应变分布。由图9 可看出：轧制第4 圈后，外径653.5 mm，轮缘完全成形，最大等效塑性应变位于踏面处，达1.93,径向变形区仅踏面上端和内径面下端较小区域尚未贴合轧辊；轧制第8 圈后，外径732.4 mm，最大等效塑性应变位于内径面上端区域，达5.34，轮箍断面心部的等效变形仍很小，约0.28；轧制第12 圈后，外径达1 003.9 mm，内径面向上端的最大等效变形增至9.30，心部累积变形达0.88。

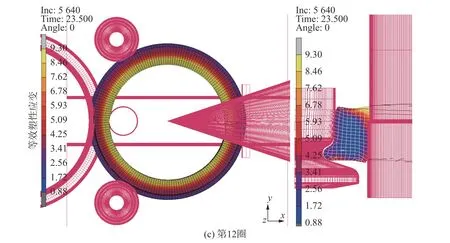
图9 轮箍轧制过程的等效塑性应变分布Fig.9 Distribution of equivalent plastic strain during tire rolling

轧制过程中，轧件断面心部塑性应变始终小于其他区域，应变大小反映变形深透程度。心部变形的深透性与轧制过程扩径效率及心部组织性能密切关系。图10 为坯料截面中心点(图2(b))在轧制过程中累积等效塑性应变的变化情况。由图10 可看出：累积等效塑性应变曲线呈阶梯变化，竖格线邻近的应变增量发生在径向变形区，竖格线之间的应变增量发生在轴向变形区。前2 圈轧制中，断面心部基本没有变形；第3 圈的径向变形区心部等效塑性应变增量约0.03，表明在轮缘和踏面成形阶段，心部基本没有变形。随壁厚减薄和径向压下的增大，径向变形区等效应变增量逐圈增加，第9 圈的径向变形区心部等效塑性应变增量达0.13，之后随芯辊进给量的减小，径向变形区等效变形增量又逐圈降低；从第9 圈开始，轴向变形区心部也发生明显的塑性变形，在第10 圈的轴向变形区断面心部的等效塑性变形增量达最大(0.10)，由此判断第9 圈后，轴向变形区环件周向延伸明显；轧制结束心部累积等效变形达到1.09。上述分析表明，当前工艺条件下，轮箍心部变形总体上较深透。

图10 轧制过程断面心部的等效塑性应变变化Fig.10 Variation of equivalent plastic strain at the center of the cross-section during rolling

2.3 轮箍轧制过程的轧辊受力

图11 为轧制过程轧辊受力情况。

图11 轧制过程中轧辊的受力情况Fig.11 Force condition of roller during rolling

由图11 可看出：轧制过程中，主辊和芯辊的受力(芯辊进给方向)基本平衡，轧制开始后，主辊和芯辊的受力逐渐增大，10 s 时(轮缘孔型充满，外径约680.0 mm)达到峰值，约1 400 kN，之后受力逐渐减小，自由轧制阶段受力约400 kN；轧制7 s 后(环件旋转约4 圈)，外径小于700.0 mm，上锥辊尚未有效压下，受力增至650 kN 并保持相对稳定，外径增至720.0 mm 后锥辊受力又缓慢增加；20 s 时(外径达912.0 mm，第11 圈)锥辊受力达峰值、约900 kN，随后锥辊受力逐渐减小。

3 结 论

提出基于轧制过程轮箍实时外径变化的辊系运动自适应控制策略，通过子程序开发实现对轮箍径轴向轧制的全过程三维有限元仿真，分析J307 轮箍轧制过程的尺寸变化和变形分布，得到以下主要结论：

1) 轮箍轧制过程中，各圈轧制变形量和扩径量均是非线性变化的。轧制至第9～13 圈时环件外径增量较大；轧制至第10 圈时环件外径增量最大，达78 mm/圈；轧制至第11 圈时轴向变形区高度压下量最大，达13.4 mm。

2) 轮箍轧制过程中，断面心部变形最小。第9 圈前断面心部主要是在径向变形区中发生变形；第9 圈后轴向变形区断面心部也发生明显塑性变形；轧制结束断面心部累积变形应变达1.09。

3) 主辊和芯辊在轮缘充满后外径约680 mm 时受力最大，约1 400 kN；锥辊在第11 圈外径达912 mm 时受力最大，约900 kN。