重载预测模型及RC连续梁桥结构反应分析

刘 浪 王 杰 叶仲韬

(1.重庆交通大学 省部共建山区桥梁及隧道工程国家重点实验室,重庆 400074;2.重庆交通大学 土木工程学院,重庆 400074;3.中铁大桥科学研究院有限公司,武汉 430034)

车辆荷载作为公路桥梁上的重要可变荷载,对桥梁结构安全性和耐久性具有很大影响[1].近年来,我国交通运输行业发展迅速,公路桥梁交通量和车载水平都大幅提升,但我国现行桥梁设计规范的荷载模型主要基于一般交通荷载调查,尚不能切实反映重载作用过程.同时,桥梁设计之初所采用的车辆荷载模型缺乏对未来车辆荷载水平的合理估计,且随着桥梁服役时间的增长,这种差异势必增大.

为提高车辆信息的准确性和可靠性,国内外学者开展了大量基于实测数据,或混合式蒙特卡罗车流模拟的车辆荷载研究[2-4],并采用概率统计方法建立车辆模型[5-6],进行车辆荷载效应的极值外推[7-9],以及重载总重或轴重阈值和模型研究[10-11].统计数据表明[12],我国卡车数量及总吨位数每年都在以不同的速率递增,即交通量和荷载等级呈现明显的非平稳增长,上述荷载模拟方法不能体现该非平稳性,导致重载作用下的结构内力验算失真.为此,本文首先基于“最不利荷载效应”提取实测重载数据,深入分析重载时间频度和重量集度的非平稳特性,然后分别基于季节时间序列(SARIMA)模型和RICE 外推理论,提出考虑非平稳性的重载模型建立方法,最后依据实际重载交通流分布,将建立的非平稳重载模型加载至桥梁有限元模型,对结构产生的荷载效应进行对比与分析.

1 实测车辆数据采集情况

本文收集了广西省内6 座大桥2007、2010 及2011年的健康监测数据,其中2011年缺少6月和10月数据,6个采集点共有6×34×30 d=6 120 d数据.考虑三车道同向行驶情况,共获得41 095 437条车辆信息记录(包括车道、时间、速度、轴重等).剔除异常记录后剩余40 513 489有效车辆.采用作者提出的基于最不利效应的重载判别方法[13],最终获得5 310 992条重载数据.

2 重载特性分析

2.1 重载的周期性分析

年平均日交通量(ADTT)只能粗略反映重载交通情况[14].为进一步了解重载时间频度的变化规律,现定义年平均小时交通量(AAHT),即1年内桥上每小时的总交通量除以实际采集天数,其中每小时总交通量统计规则为:将1 d划分为24个时段,0～1时刻到达的车辆统计为1时车辆,以此类推.统计出3年24 h的年平均小时交通量,如图1所示.由图1可知,各年的交通量具有明显的周期性,一天内各小时的交通量差异显著,其中,9:00～13:00出现单峰值,约占重车数量的33%,23:00～1:00出现谷值.图示结果说明AAHT能够反映交通量的周期性和非平稳增长.

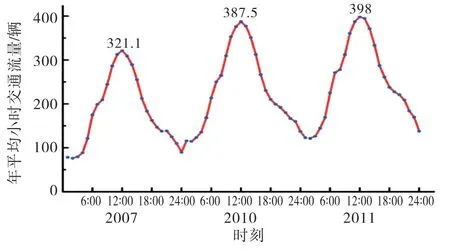
图1 实测重载的年平均小时交通量

2.2 重载车型统计分析

考虑到重载的空间分布与荷载特性参数差异较大,现将提取的重载数据按车道和车轴数进行分类统计,结果见表1.

表1 各车道重载车型占比(%)

1、2、3车道重载的占比分别为51.79%、47.58%、0.63%,表明重载对行驶车道具有很强的选择性;各车道上5轴车最多,均占到了50%以上,其次数量较多的是4轴车,为典型的中重型货车.各车道上10和11轴车数据量极少,后续分析可不予考虑.

3 重载交通量预测模型

3.1 SARIMA模型概述

因可以准确模拟并预测季节性序列,SARIMA模型在疾病数据预测方面得到了广泛应用[15-16].根据前文的重载周期性分析结果,本文采用SARIMA 模型建立非平稳重载交通量预测模型.SARIMA 模型包含自回归阶数p、差分阶数d、移动平均阶数q、季节性自回归阶数P、季节性差分阶数D、季节性移动平均阶数Q和周期s7个基本参数,记为SARIMA(p,d,q)×(P,D,Q)S形式.构建模型的步骤包括:对时序数据进行平稳性检测以及处理、噪声检测、模型定阶、残差及模型检验、模型构建.

3.2 交通量预测模型的建立

首先对序列进行平稳性检测.使用Matlab的adftest函数,对AAHT 序列分别进行无截距和无趋势项、有截距项和无趋势项、有截距项和有趋势项3种情况的单位根检验,返回的DF 值分别为-0.506 0、-1.537 2、-1.863 1,adftest函数返回值h=0,说明AAHT 序列是非平稳的.

对AAHT 序列进行一阶差分得到d AAHT 序列,再对该序列进行单位根检验,adftest函数返回值h=1,说明该序列平稳,绘制其自相关和偏自相关系数,如图2所示.从图2看出,该序列具有明显的相关性,即使以24为1个周期进行滞后,仍表现出较高的相关性.另外,自相关图在4阶后出现拖尾且阶数较大,偏自相关图在1阶后出现拖尾,因此初步确定参数p取值范围为1～4,参数q取1.

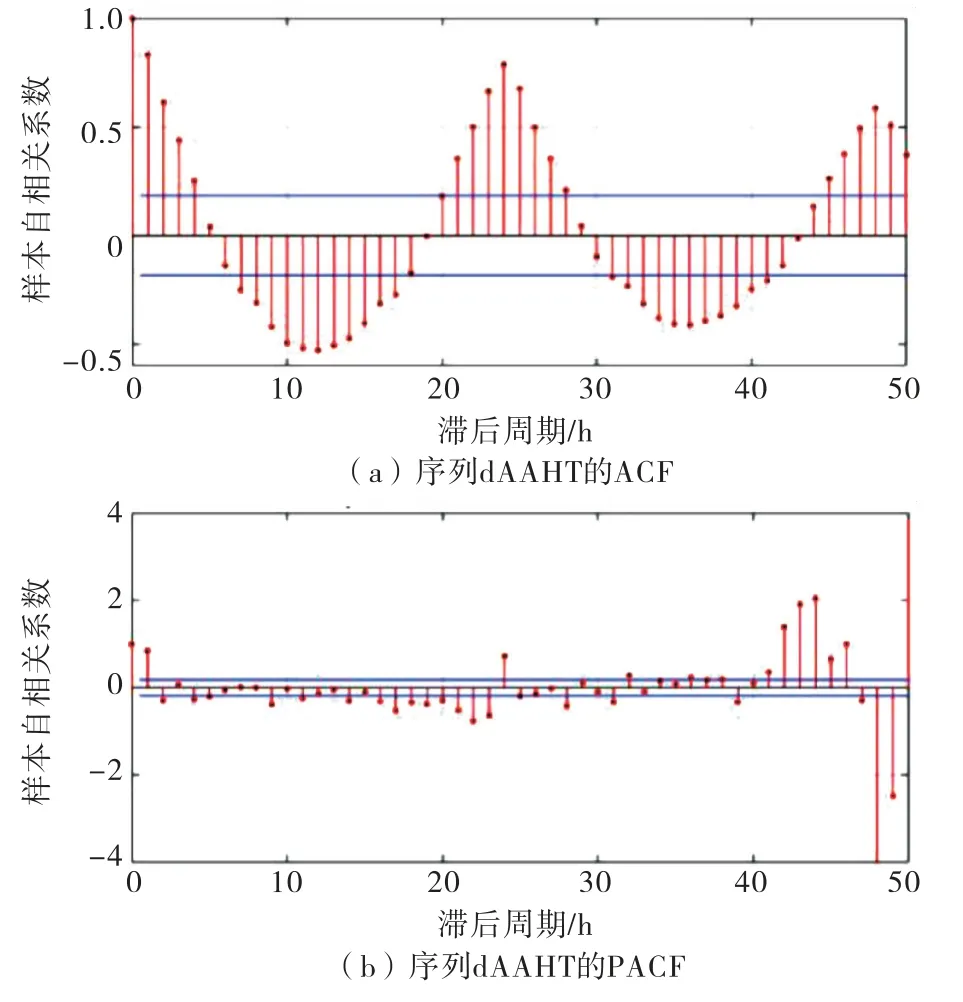
图2 d AAHT 序列的自相关和偏自相关系数

再对d AAHT 序列进行24 步季节差分得到DAAHT 序列,验证该序列的平稳性、自相关和季节性:单位根检验adftest 函数返回值h=1,说明DAAHT 序列平稳,绘制该序列的自相关和偏自相关系数如图3所示.

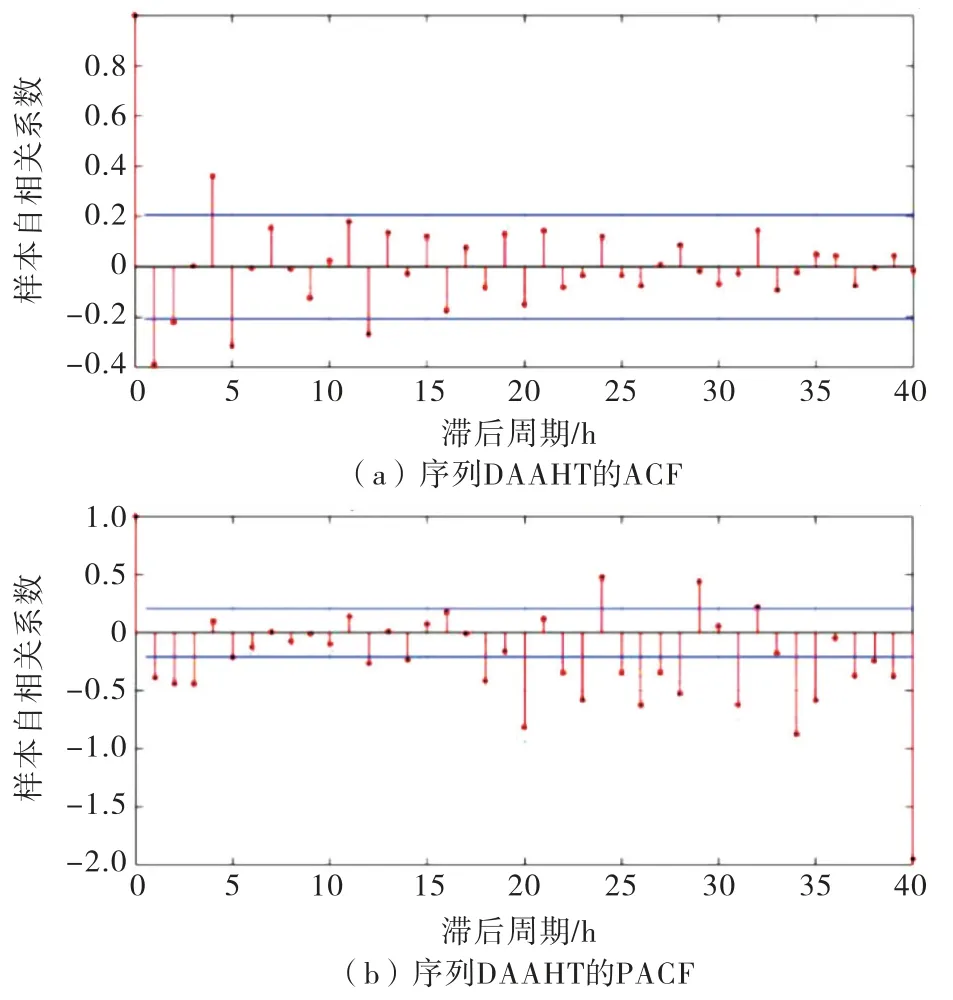
图3 序列DAAHT 的自相关和偏自相关系数

由图可知,大部分系数点在可信范围内,仅有少量系数点落在置信区间外,表明原时间序列的季节性被消除.自相关图在3阶后出现拖尾且阶数较大,偏自相关图在2阶后出现拖尾,因此,初步确定参数Q为1～3,参数P=2.以上平稳处理过程进行了一次差分,故参数d和D为1,周期参数s为24,重复上述步骤共建立12个SARIMA 模型,再根据最小AIC值=513.318 8,最终确定交通量预测模型为SARIMA(2,1,1)×(2,1,3)24,模型残差分析如图4所示.其中,残差标准差分布图4(a)中,残差标准差基本位于-2到2之间;残差QQ 图4(b)中,残差基本都落在45度线上,说明残差符合正态性假设;残差ACF图4(c)中,残差的自相关值基本都处于0.2与-0.2的两条虚线之间,表明残差具有随机性.综上可知,重载交通量预测模型SARIMA(2,1,1)×(2,1,3)24是合理有效的.

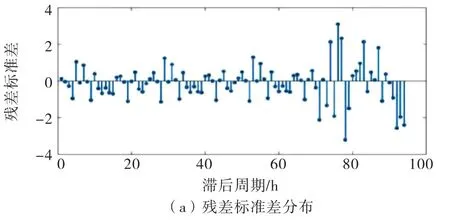
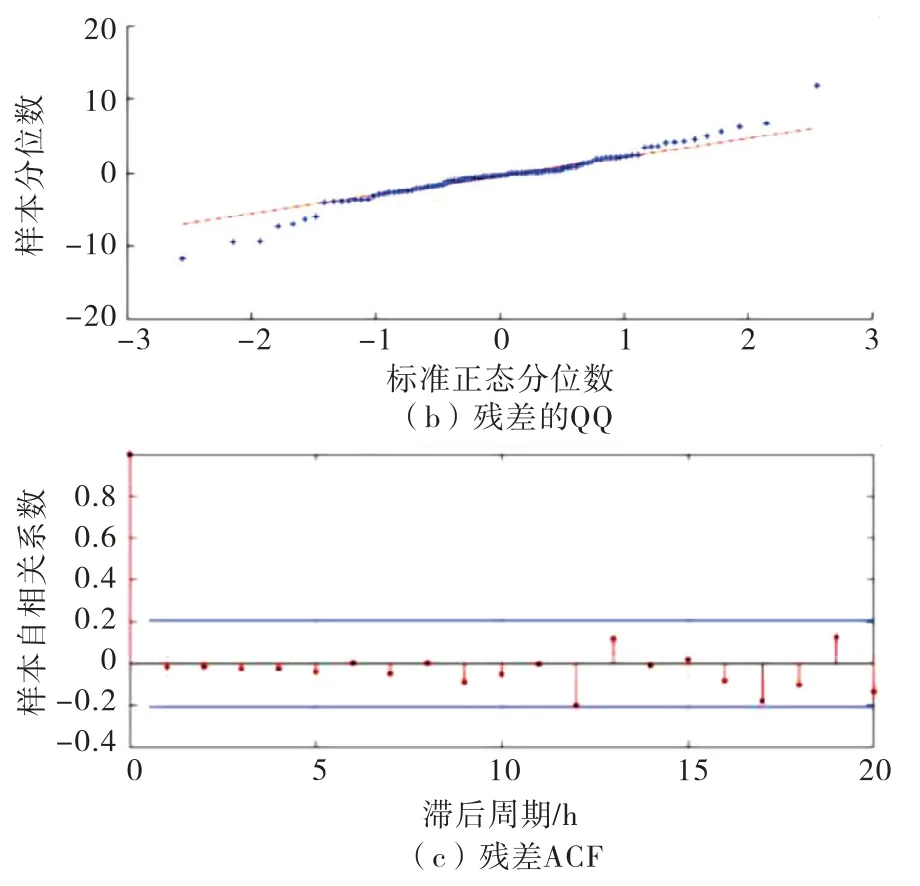
图4 SARIMA 模型残差分析

3.3 模型验证以及预测应用

运用建立的SARIMA(2,1,1)×(2,1,3)24模型预测2010和2011年重载AAHT,将预测值与实测值进行对比如图5所示.

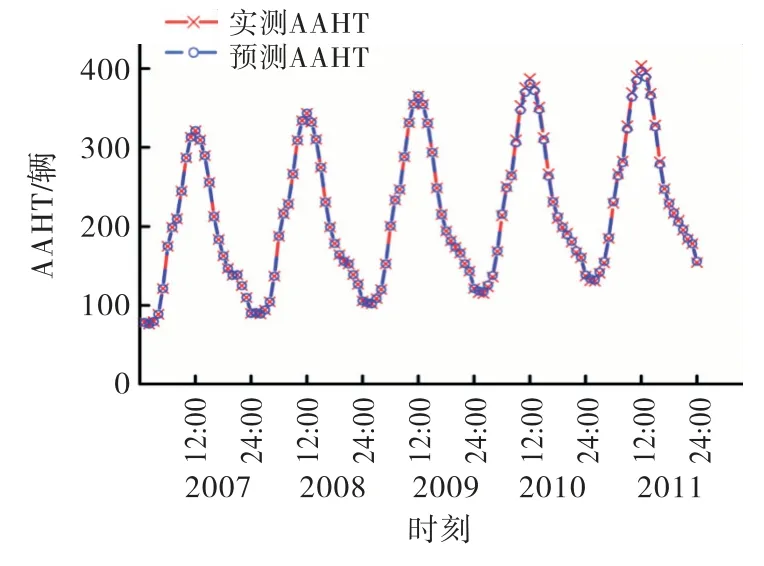
图5 2007～2011年的AAHT 预测值与实测值比较

从图5可以看出,预测数据曲线与实测数据曲线吻合良好,说明本文建立的SARIMA 模型能够准确地模拟并预测重载交通量的非平稳变化.运用该模型预测20年后的重载交通量,结果见表2.总体上,2031年的日平均交通量比2011年增加了约1.26倍.

表2 2011年的实测AAHT与2031年的预测AAHT

4 基于RICE公式的重载极值外推

4.1 RICE理论公式简介

由于车载效应符合高斯平稳过程,基于RICE 公式的极值外推法在车载效应外推研究上得到广泛应用[17-19].类似地,重载总重及轴重亦符合平稳高斯过程,故可基于RICE 公式进行极值外推.本文使用RICE公式对重载数据拟合过程中涉及的K-S检验部分,根据柯尔莫哥洛夫公式,近似转换成计算β值来保证拟合效果:

式中:N是起始点x0右侧数据的间隔数;Q k是一个单调递减函数;D是累积分布统计量.

确定RICE公式参数后,可通过极值外推方法,外推任意重现期内的极值总重或轴重.需注意的是,数据分组和间隔数N会影响拟合结果及其拟合优度,重现期需是观测周期的倍数.更详尽的RICE 外推理论及方法可参见文献[20].

4.2 重载荷载极值外推模型

综合考虑总重、轴重和轴距对荷载效应的影响,以及所有轴重不可能同时出现最大值这一现实,本文先进行总重及最大轴重的极值外推,其它轴重则根据实测数据按比例反向分配,建立重载模型.下面以5轴重载为例进行说明.首先拟合出5轴重载的轴重和轴距概率分布函数,然后通过K-S检验找出最优拟合分布,如图6所示.

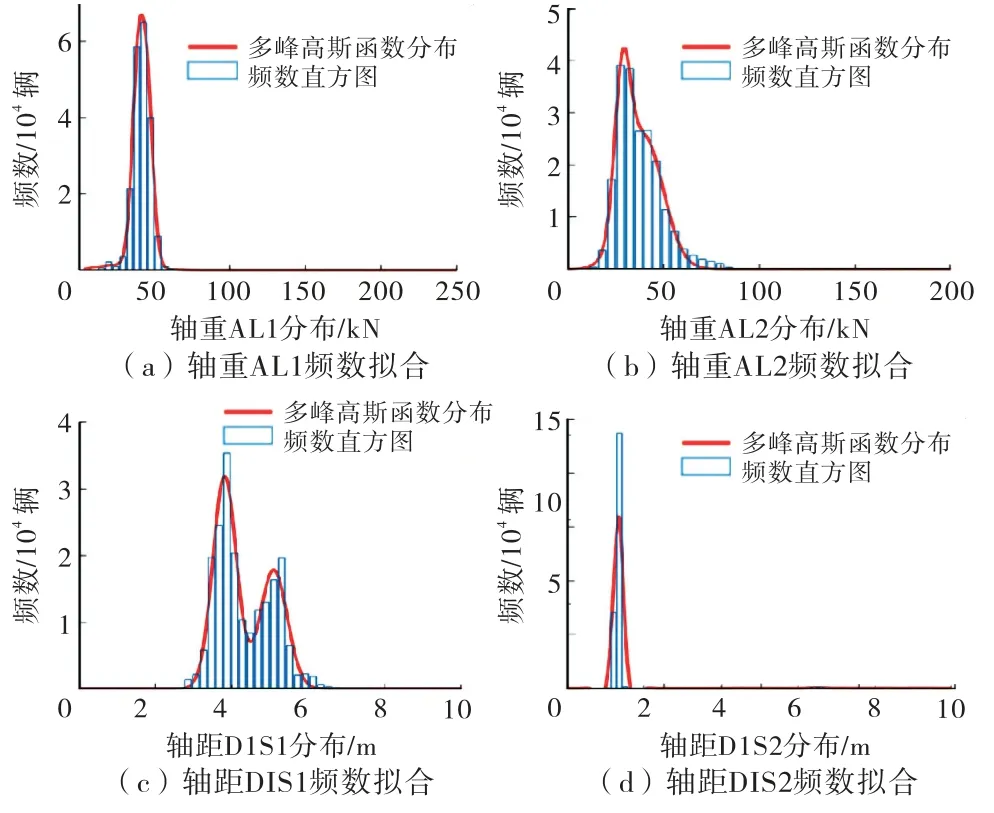
图6 5轴重载参数拟合

限于篇幅,文中仅展示轴重1、轴重2和轴距1、轴距2的拟合结果.其中,非参高斯核函数分布采用期望值作为拟合代表值,其它分布使用0.95分位值作为代表值.各轴重、轴距的拟合结果见表3.

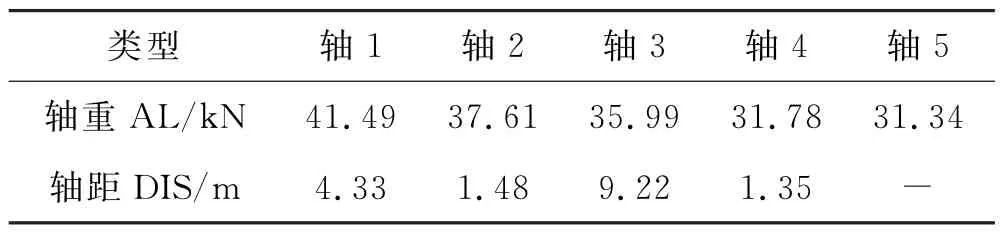
表3 5轴重载各参数拟合代表值

由表3可知,轴1为最重轴.选择5轴重载的轴重AL1和总重GVW 的穿越频数进行RICE拟合,如图7所示.其中,图7(a)为轴重AL1拟合,bin=50,N=35;图7(b)为总重拟合,bin=40,N=33,则1950 年重现期内轴重和总重的外推极值分别为185.81 k N 和605.51 k N.再根据表3中各轴重拟合代表值的比例对其它轴重进行分配,结合轴距拟合代表值,即可建立非平稳重载模型.类似地,对其它车型重复以上过程,得到所有重载模型见表4.

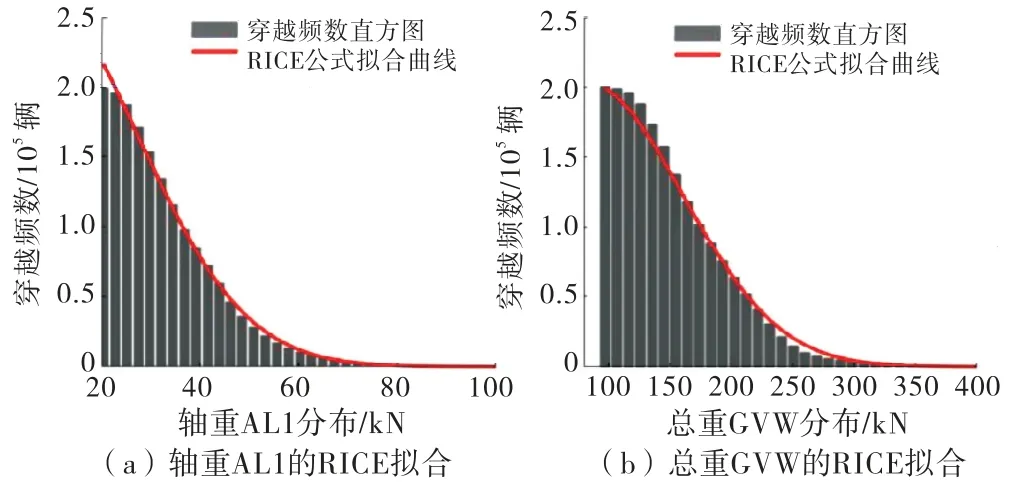
图7 5轴重载最大轴重和总重的RICE拟合

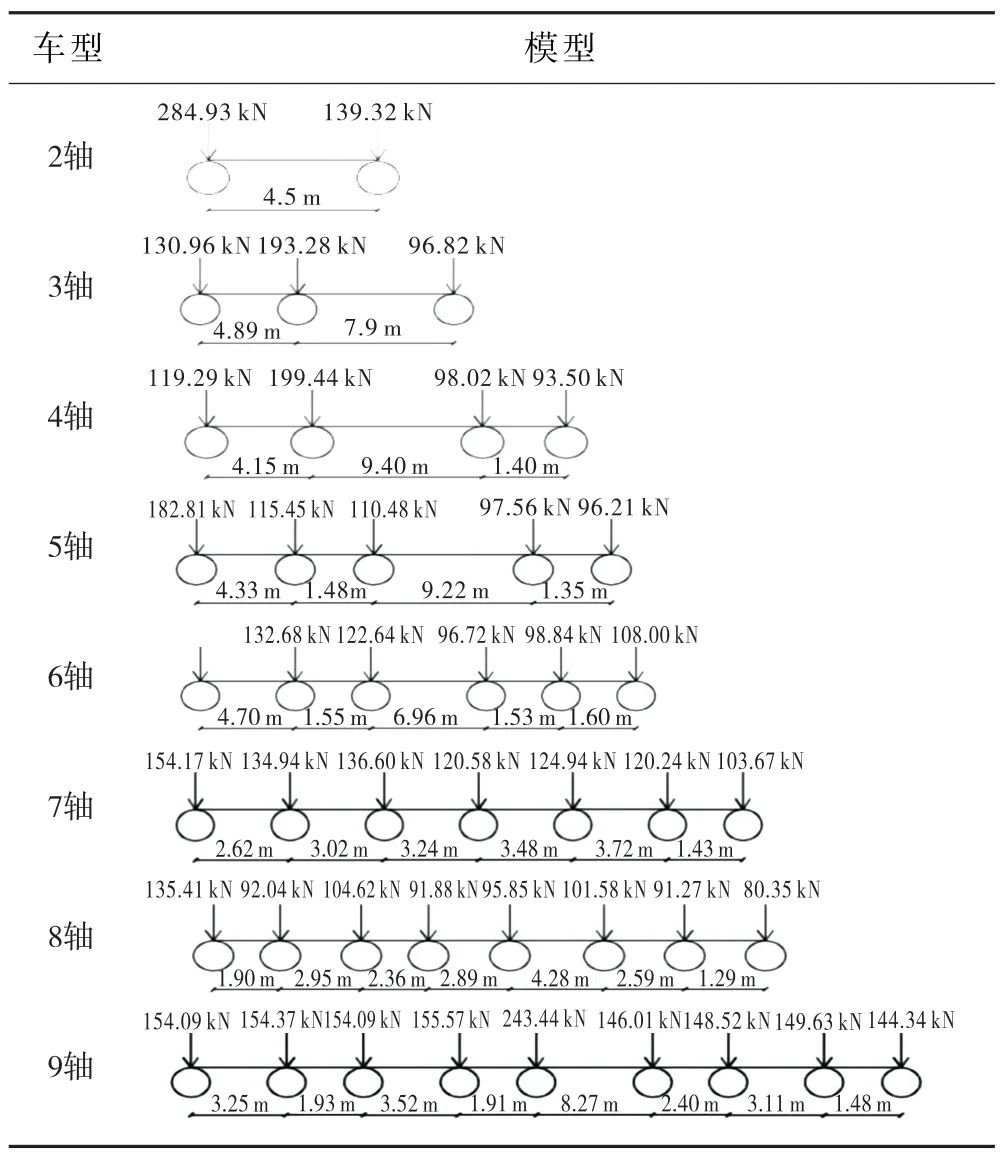
表4 考虑荷载水平非平稳性的重载模型

5 非平稳重载作用下的桥梁受力分析

5.1 桥梁有限元模型

选择某3 m×20 m 的三跨T 型预应力连续梁桥为研究对象,该桥设计基准期为100年,设计使用年限100年.全桥单向三车道,路基宽度为16.0 m,桥面宽15.5 m,公路等级为一级,其横断面如图8所示.依据该T 型连续梁桥设计参数建立的有限元模型如图9所示.

图8 跨中截面横断面(单位:mm)

图9 T 型预应力连续梁桥有限元模型

5.2 桥梁结构的反应

为充分体现交通量变化对桥梁结构内力的影响,本文综合考虑交通量变化、车长以及桥梁跨径等因素,选择出现峰值的12时的年平均30 s交通量进行布载.2011年及2031年12时的计算交通量分别为398辆和693辆,则30s交通量分别为4辆和6辆;因重载主要在1、2车道行驶,3车道仅有少量重载,故考虑以下两种情况:①2011年1～3车道的车数分别为2、2、0辆,2031年交通量增加后各车道车数分别为3、3、0辆;②2011年1～3车道的车数分别为1、2、1辆,2031年交通量增加后各车道车数分别为2、3、1辆.车间距依据《公路桥涵设计通用规范》(JTG D60—2015)确定为2.2 m[21].根据前文车道、车型占比等统计结果,选择主要的4轴和5轴车型,以及产生较大弯矩值的2轴、6轴和9轴车进行工况组合.提取产生最大中跨跨中截面弯矩的20个车型组合见表5.

考虑自重、桥面铺装和预应力等恒载,按照承载能力极限状态,与表5中的重载进行荷载组合,加载至桥梁有限元模型,计算得到交通量增加前后桥梁跨中截面弯矩、支座负弯矩和主梁最大应力,如图10所示.由图10可知,无论是否考虑交通量增长,桥梁跨中弯矩均大于现行中美规范设计值,约为中国规范的1.21～1.55 倍,美国规范的1.13～1.45 倍.对比2011年与2031年的计算结果,发现交通量增加后,图10(a)和(b)中跨中弯矩和支座弯矩最大增幅分别为10%和22%;图10(c)中梁底混凝土应力增大,最大增幅为14%.因为1、4、5、7等9个工况下重载跨过支座布置,减轻了中跨的弯矩效应,增加了支座位置及边跨的弯矩效应,使得跨中与支座呈现相反的增减趋势.总体而言,重载交通的非平稳增长使得结构的内力有所增加,但梁底混凝土总体仍处于受压状态,应力大小未超出规范限值,结构不会出现较大的变形或开裂等破坏,但需要关注梁体出现局部细微裂缝等损伤情况.同时,重载在桥面的纵、横向空间分布特性对结构内力的大小影响较甚,在选取内力控制截面时应予以考虑.

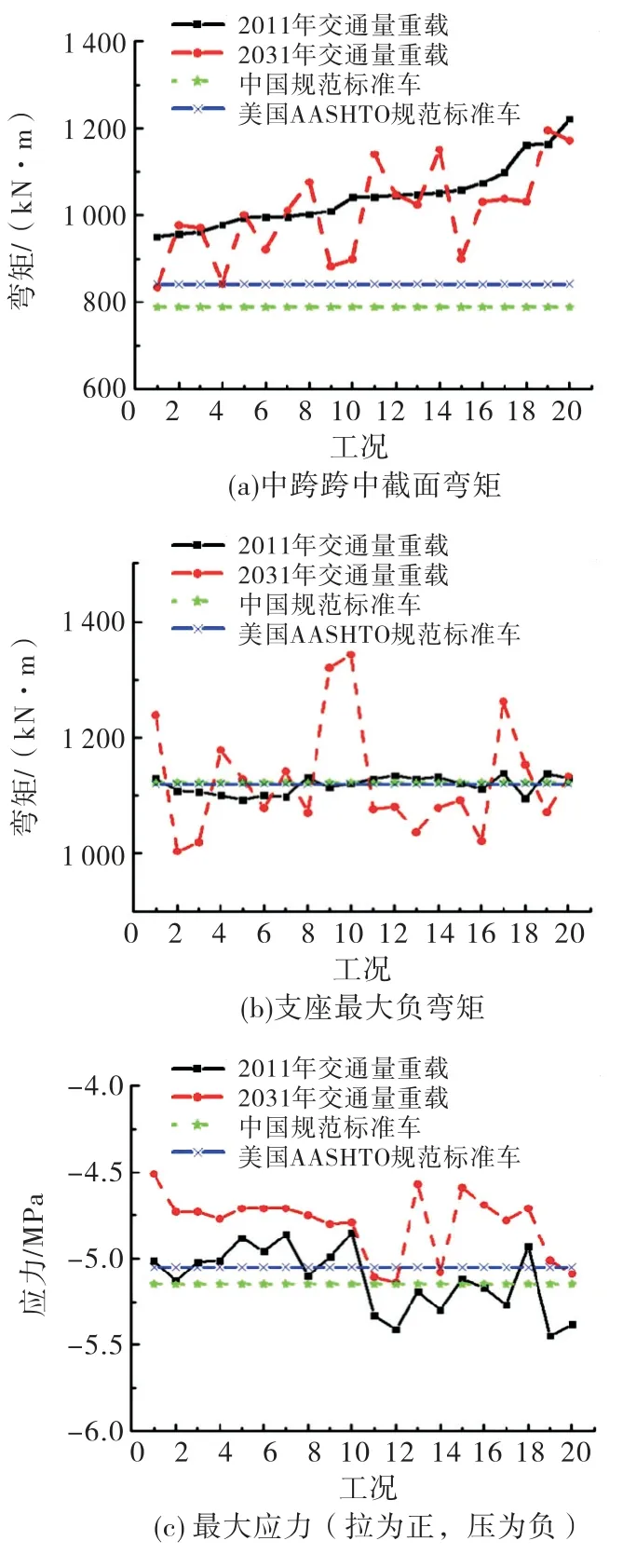
图10 重载交通量增加前后的桥梁受力分析

6 结论

本文基于“最不利效应”提取了实测重载数据,对重载交通量和荷载水平的非平稳特性进行了分析,融合SARIMA 模型和RICE 极值外推方法,建立了非平稳重载模型,以实际重载交通情况进行有限元模型加载,分析了非平稳重载作用下桥梁结构内力的变化情况.主要获得以下结论:

1)重载交通量具有明显的周期性和增长趋势,通行量单峰值在11～13时,行驶车道具有明显的选择性.年平均小时交通量(AAHT)能够有效地反映重载交通量的非平稳性,本文建立的SARIMA 模型能够准确地模拟并预测非平稳重载交通量,2031 年的预测重载交通量比2011年增长约126%.

2)基于RICE 外推公式提出了考虑荷载集度非平稳的重载模型建立方法,通过对重载总重和最大轴重的极值外推,以及实测轴重数据的拟合代表值,对其它轴重进行按比例反向分配,并结合实测轴距拟合代表值,建立重现期内可能出现的最大重载模型.

3)桥梁有限元模型加载计算结果表明,考虑重载非平稳性后,桥梁跨中弯矩和支座弯矩最大增幅分别为10%和22%,两者的增减趋势近似相反;结构所受应力总体增大,最大增幅为14%.总体上,重载交通的非平稳增长使得结构的内力增大,应注意梁体出现局部细微裂缝等损伤;同时,选取内力控制截面时应适当考虑重载在桥面的纵、横向空间分布特性.