三元变系数Euler函数非线性方程的正整数解①

戴妍百， 高丽

延安大学 数学与计算机科学学院，陕西 延安 716000

对于任意正整数n,欧拉函数φ(n)定义为不大于n且与n互素的正整数的个数.欧拉函数在数论中有着重要的作用,有关欧拉函数的性质以及欧拉方程引起了很多学者的研究兴趣[1-3]．

近年来,文献[1,4-12]分别讨论了当k=2,3,4,5,6,7,8,9,11,12时,欧拉方程φ(xy)=k(φ(x)+φ(y))的可解性问题. 对于二元变系数欧拉函数方程φ(xy)=mφ(x)+nφ(y),文献[13]讨论了当m=5,n=7时的可解性问题,文献[14]讨论了当m=7,n=9时的可解性问题.文献[15-17]分别讨论了当k=3,4,5时,三元欧拉函数方程φ(xyz)=k(φ(x)+φ(y)+φ(z))的全部正整数解.对于含常数的二元变系数方程φ(xy)=k1φ(x)+k2φ(y)+k,文献[18-19]利用整数的分解性质讨论了(k1,k2,k)=(7,8,16),(4,7,28)时的可解性问题.文献[20]讨论了k=6,28时三元变系数方程φ(xyz)=2φ(x)+3φ(y)+4φ(z)-k的可解性问题.本文利用欧拉函数的性质与初等数论方法,讨论并证明了

φ(xyz)=aφ(x)+bφ(y)+cφ(z)-m

当(a,b,c)=(2,3,4)且m=8时正整数解的情况,并给出了该欧拉方程的全部正整数解．

引理1[21](φ(m)的乘积公式) 对m>1,我们有

其中,p是m的素因数．

引理 2[21]欧拉函数φ(m)具有下列性质:

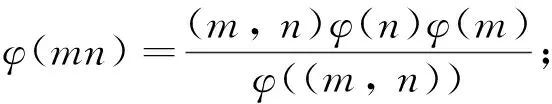
(ii) 当(m,n)=1时,φ(mn)=φ(m)φ(n);

(iii) 当m≥3时,φ(m)必为偶数．

定理1欧拉方程φ(xyz)=2φ(x)+3φ(y)+4φ(z)-8一共有32组正整数解,分别为:

(x,y,z)=(1,7,9),(1,7,18),(1,9,7),(1,9,14),(1,14,9),(1,18,7),(2,7,9),(2,9,7),(2,12,4),(1,11,8),(1,11,10),(2,11,5),(3,12,1),(3,5,4),(4,5,3),(1,4,2),(1,6,2),(2,3,2),(2,4,1),(2,6,1),(3,3,1),(3,3,2),(3,6,1),(6,3,1),(1,4,4),(1,4,6),(2,3,4),(2,4,3),(5,8,1),(5,12,1),(8,5,1),(12,5,1)．

证方程φ(xyz)=2φ(x)+3φ(y)+4φ(z)-8有正整数解的必要条件是

(φ(x)-3)(φ(y)-2)≤2

事实上,对于欧拉函数方程

φ(xyz)=2φ(x)+3φ(y)+4φ(z)-8

(1)

利用欧拉函数的性质得

由引理2的(i)可知

对(1)式进行化简,可得

故有

(φ(x)-3)(φ(y)-2)≤2

(2)

由上述过程可知,方程(1)有解时,(2)式必然成立.故对二元一次不等式(2)进行讨论:

当(φ(x)-3)(φ(y)-2)<0时,有φ(x)=1,2,φ(y)≥4; 或φ(x)≥4,φ(y)=1．

当(φ(x)-3)(φ(y)-2)=0时,有φ(x)=3或φ(y)=2.由引理2的(iii)知φ(x)=3不存在,舍去．

当(φ(x)-3)(φ(y)-2)=1时,有φ(x)=4,φ(y)=3; 或φ(x)=2,φ(y)=1.由引理2的(iii)知φ(x)=4,φ(y)=3不存在,舍去．

当(φ(x)-3)(φ(y)-2)=2时,有φ(x)=5,φ(y)=3; 或φ(x)=4,φ(y)=4; 或φ(x)=1,φ(y)=1. 由引理2的(iii)知φ(x)=5,φ(y)=3不存在,舍去．

综上所述,可得方程(1)有解的7种情况,下面进行分类讨论给出方程的解．

情况1当φ(x)=1,φ(y)≥4时,代入方程(1)进行化简,得

(φ(y)-4)(φ(z)-3)≤6

情况1.1 当φ(y)=4时,方程(1)为φ(xyz)=4φ(z)+6．

当φ(z)=1时,φ(xyz)=10,即xyz=11,12,又因为x=z=1,2,y=5,8,10,12,经检验,此时方程(1)无解．

当φ(z)=2时,φ(xyz)=14,这样的x,y,z不存在,因此方程(1)无解．

当φ(z)=4时,φ(xyz)=22,即xyz=23,46,又因为x=1,2,y=z=5,8,10,12,经检验,此时方程(1)无解．

当φ(z)=6时,φ(xyz)=30,即xyz=31,62,又因为x=1,2,y=5,8,10,12,z=7,9,14,18,经检验,此时方程(1)无解．

当φ(z)=8时,φ(xyz)=38,即这样的x,y,z不存在,因此方程(1)无解．

当φ(z)≥10时,φ(xyz)=4φ(z)+6,将x=1,2,y=5,8,10,12代入方程(1),经检验,不存在满足φ(xyz)=4φ(z)+6且φ(z)≥10的x,y,z,因此方程(1)无解．

情况1.2 当φ(y)=6时,此时φ(z)-3≤3,即φ(z)=1,2,4,6．

当φ(z)=1时,φ(xyz)=16,即xyz=17,32,34,40,48,60,又因为x=z=1,2,y=7,9,14,18,经检验,此时方程(1)无解．

当φ(z)=2时,φ(xyz)=20,即xyz=25,33,44,50,66,又因为x=1,2,y=7,9,14,18,z=3,4,6,经检验,此时方程(1)无解．

当φ(z)=4时,φ(xyz)=28,即xyz=29,58,又因为x=1,2,y=7,9,14,18,z=5,8,10,12,经检验,此时方程(1)无解．

当φ(z)=6时,φ(xyz)=36,即xyz=37,57,63,74,76,108,114,126,又因为x=1,2,y=z=7,9,14,18,经检验,此时方程(1)有解,为(x,y,z)=(1,7,9),(1,7,18),(1,9,7),(1,9,14),(1,14,9),(1,18,7),(2,7,9),(2,9,7)．

情况1.3 当φ(y)=8时,此时φ(z)-3≤1,即φ(z)=1,2,4．

当φ(z)=1时,φ(xyz)=22,即xyz=23,46,又因为x=z=1,2,y=15,16,20,24,30,经检验,此时方程(1)无解．

当φ(z)=2时,φ(xyz)=26,这样的x,y,z不存在,因此方程(1)无解．

当φ(z)=4时,φ(xyz)=34,这样的x,y,z不存在,因此方程(1)无解．

情况1.4 当φ(y)=10时,此时φ(z)-3≤1,即φ(z)=1,2,4．

当φ(z)=1时,φ(xyz)=28,即xyz=29,58,又因为x=z=1,2,y=11,12,经检验,此时方程(1)无解．

当φ(z)=2时,φ(xyz)=32,即xyz=51,64,68,80,96,102,120,又因为x=1,2,y=11,12,z=3,4,6,经检验,此时方程(1)有解,为(x,y,z)=(2,12,4)．

当φ(z)=4时,φ(xyz)=40,即xyz=41,88,100,110,132,150,又因为x=1,2,y=11,12,z=5,8,10,12,经检验,此时方程(1)有解,为(x,y,z)=(1,11,8),(1,11,10),(2,11,5)．

情况1.5 当φ(y)≥12时,此时φ(z)-3≤0,即φ(z)=1,2．

当φ(z)=1时,将x=z=1,2代入方程(1),经检验,不存在满足φ(xyz)=3φ(y)-2且φ(y)≥12的x,y,z,因此方程(1)无解．

同理当φ(z)=2时,方程(1)无解．

情况2当φ(x)=2,φ(y)≥4时,方程(1)化简为

(φ(y)-2)(2φ(z)-3)≤2

情况2.1 当φ(y)=4时,此时2φ(z)-3≤1,即φ(z)≤2．

当φ(z)=1时,φ(xyz)=12,即xyz=13,21,26,28,36,42,又因为x=3,4,6,y=5,8,10,12,z=1,2,经检验,此时方程(1)有解,为(x,y,z)=(3,12,1)．

当φ(z)=2时,φ(xyz)=16,即xyz=17,32,34,40,48,60,又因为x=z=3,4,6,y=5,8,10,12,经检验,此时方程(1)有解,为(x,y,z)=(3,5,4),(4,5,3);

情况2.2 当φ(y)≥6时,此时2φ(z)-3≤0,即φ(z)=1．

当φ(z)=1时,将z=1,2,x=3,4,6代入方程(1),经检验,不存在满足φ(xyz)=3φ(y)且φ(y)≥6的x,y,z,因此方程(1)无解．

情况3当φ(x)≥4,φ(y)=1时,方程(1)化简为

(φ(x)-4)(φ(z)-2)≤3

情况3.1 当φ(x)=4时,此时方程(1)为φ(xyz)=4φ(z)+3．

由此得φ(xyz)为奇数,由引理2的(iii)可知方程(1)无解．

情况3.2 当φ(x)=6时,此时φ(z)-2≤1,即φ(z)=1,2．

当φ(z)=1时,φ(xyz)=11,因φ(xyz)为奇数,由引理2的(iii)可知方程(1)无解．

当φ(z)=2时,φ(xyz)=15,因φ(xyz)为奇数,由引理2的(iii)可知方程(1)无解．

情况3.3 当φ(x)≥8时,此时φ(z)-2≤0,即φ(z)=1,2．

当φ(z)=1时,将y=z=1,2代入方程(1),经检验,不存在满足φ(xyz)=2φ(x)-1且φ(x)≥8的x,y,z,因此方程(1)无解．

同理当φ(z)=2时,方程(1)无解．

情况4当φ(y)=2时,方程(1)化简为

(φ(x)-2)(φ(z)-1)≤1

情况4.1 当φ(z)=1时,方程(1)为φ(xyz)=2φ(x)+2．

当φ(x)=1时,φ(xyz)=4,即xyz=5,8,10,12,又因为x=z=1,2,y=3,4,6,经检验,此时方程(1)有解,为(x,y,z)=(1,4,2),(1,6,2),(2,3,2),(2,4,1),(2,6,1)．

当φ(x)=2时,φ(xyz)=6,即xyz=7,9,14,18,又因为x=y=3,4,6,z=1,2,经检验,此时方程(1)有解,为(x,y,z)=(3,3,1),(3,3,2),(3,6,1),(6,3,1)．

当φ(x)=4时,φ(xyz)=10,即xyz=11,12,又因为x=5,8,10,12,y=3,4,6,z=1,2,经检验,此时方程(1)无解．

当φ(x)=6时,φ(xyz)=14,这样的x,y,z不存在,因此方程(1)无解．

当φ(x)≥8时,φ(xyz)=2φ(x)+2,将y=3,4,6,z=1,2代入方程(1),经检验,不存在满足φ(xyz)= 2φ(x)+2且φ(x)≥8的x,y,z,因此方程(1)无解．

情况4.2 当φ(z)=2时,此时φ(x)-2≤1,即φ(x)=1,2．

当φ(x)=1时,φ(xyz)=8,即xyz=15,16,20,24,30,又因为x=1,2,y=z=3,4,6,经检验,此时方程(1)有解,为(x,y,z)=(1,4,4),(1,4,6),(2,3,4),(2,4,3)．

当φ(x)=2时,φ(xyz)=10,即xyz=11,12,又因为x=y=z=3,4,6,经检验,此时方程(1)无解．

情况4.3 当φ(z)≥4时,(φ(x)-2)≤0,即φ(x)=1,2．

当φ(x)=1时,将x=1,2,y=3,4,6代入方程(1),经检验,不存在满足φ(xyz)=4φ(z)且φ(z)≥4的x,y,z,因此方程(1)无解．

同理当φ(x)=2时,方程(1)无解．

情况5当φ(x)=2,φ(y)=1时,代入方程(1)可得φ(xyz)=4φ(z)-1,因φ(xyz)为奇数,由引理2的(iii)可知方程(1)无解．

情况6当φ(x)=4,φ(y)=4时,代入方程(1)可得φ(xyz)=4φ(z)+12≥16φ(z),即φ(z)=1,此时φ(xyz)=16,即xyz=17,32,34,40,48,60,又因为x=y=5,8,10,12,z=1,2,经检验,此时方程(1)有解,为(x,y,z)=(5,8,1),(5,12,1),(8,5,1),(12,5,1)．

情况7当φ(x)=1,φ(y)=1时,代入方程(1)可得φ(xyz)=4φ(z)-3,因φ(xyz)为奇数,由引理2的(iii)可知方程(1)无解．

综上所述,可得方程φ(xyz)=2φ(x)+3φ(y)+4φ(z)-8一共有32组正整数解．