具有环境传播和生理年龄结构的霍乱模型研究
2023-05-07亢跃男郭文丹聂麟飞
亢跃男, 郭文丹, 聂麟飞
(新疆大学 数学与系统科学学院, 新疆 乌鲁木齐 830046)
霍乱是一种通过摄入由霍乱弧菌污染的水或食物引起的急性肠道传染病.霍乱弧菌可以在环境中存活1~3周, 甚至更长时间, 它主要通过人与人直接传播或环境与人间接传播.自1817年以来霍乱发生了七次世界性大流行, 据世卫组织估计, 每年大约有130万至400万例病例, 以及2.1万至14.3万例死亡[1].时至今日, 霍乱仍是威胁全球人类生命健康的重大公共卫生问题.
在过去几十年中, 国内外学者建立了许多具有人与人之间或环境与人之间传播的霍乱常微分方程模型[2-5],研究了其无病平衡态和地方病平衡态的存在性与稳定性.众所周知,在生物种群中异质性是广泛存在的,不同年龄段的人接触疾病的概率是不同的,从而感染疾病的风险也不同,因此,研究具有年龄结构的传染病模型是很有必要的.为此,一些国内外研究者建立了具有年龄结构的传染病数学模型[6-10],讨论了年龄在传染病传播中的影响.例如,Lin等[8]提出的类年龄结构霍乱模型中考虑了感染者的感染年龄和环境中病原体的仓室年龄,讨论了无病平衡态和地方病平衡态的局部稳定性和全局稳定性.Yang等[9]建立了偏微分方程和常微分方程耦合的人群具有生理年龄的霍乱环境传播模型,给出了疾病的基本再生数,讨论了年龄对霍乱传播的影响.基于上述讨论,本文将建立人群和环境病毒均有生理年龄的霍乱传播偏微分方程模型,讨论各类平衡态的存在性和稳定性.
1 模型的建立与正解的存在唯一性
将某地区的人群分为三类: 易感者类,感染者类和恢复者类,其在t时刻a年龄的密度分别为S(t,a),I(t,a),R(t,a),记环境中t时刻年龄为a的霍乱弧菌浓度为P(t,a).总人口的年龄密度函数为N(t,a)=S(t,a)+I(t,a)+R(t,a).根据病原体在人群和环境之间的传播规律,易感者以λ1(t,a)的速率接触染病者而被感染,以λ2(t,a)的速率接触环境中的病毒而被感染,这里定义如下感染力函数[11]:
其中:k(a)表示接触率;β1(a)表示感染者的传染率;β2(a)表示环境中病原体的传染率.进一步,令b(a)和μ(a)分别表示单位时间内年龄为a的人均出生率和死亡率,γ(a)和θ(a)分别表示人类年龄依赖的治疗率和自然恢复率,ξ(a)表示感染者的病毒脱落率,δ(a)表示环境中病原体的自然死亡率.
基于上述假设,建立具有环境传播和年龄结构的霍乱模型
(1)
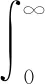
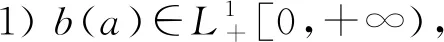
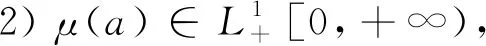
把模型(1)中的前三个方程相加,得
(2)
模型(2)是标准的Mckendrik-Von Forester方程,沿特征线t-a=c(常数)[12]解得
为保证关于年龄稳态的存在性,假设人口的净再生率等于1,即人口总数处于平衡状态,则
从而,模型(2)的稳态解为
初始人口分布满足:S0(a)≥0,I0(a)≥0,R0(a)≥0,S0(a)+I0(a)+R0(a)=N∞(a),则
对模型(1)进行归一化处理,令
则
从而,模型(1)可改写为
(3)
式中:s(t,0)=1,i(t,0)=r(t,0)=p(t,0)=0,t>0.s(0,a)=s0(a),i(0,a)=i0(a),r(0,a)=r0(a),p(0,a)=p0(a),且s(t,a)+i(t,a)+r(t,a)=1.
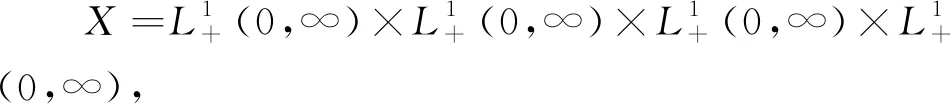

则模型(3)可化为抽象柯西问题
(4)
式中:u(t)=(s(t,·),i(t,·),r(t,·),p(t,·))T,u0(a)=(s0(a),i0(a),r0(a),p0(a))T.显然,当t>a时,算子A是C0-半群T(t)的无穷小生成元,并且算子B在空间X上连续Frechet可微.定义两个集合F={(s,i,r,p)∈X:s≥0,i≥0,r≥0,p≥0}和F0={(s,i,r,p)∈X:0≤s≤1,0≤i≤1,0≤r≤1,0≤p≤K},其中K是正常数.与文献[13]中引理3.1的证明类似,关于模型(4)有以下的结论.
引理1F0是关于u的正不变集,并且对于X上的初值u0∈F∩D(A),模型(4)存在唯一的经典解.
2 无病平衡态的稳定性
利用特征方程推导基本再生数R0的精确表达式,并证明无病平衡态的局部和全局渐近稳定性.显然,模型(3)存在无病平衡态E0=(1,0,0,0).令

(5)
式中
(6)
式中
(7)
利用常数变易法求解模型(6)得
(8)
(9)
上式左右两边同时除以V0(V0≠0),得到特征方程
(10)
定义基本再生数[14]R0:=G(0),即
现讨论无病平衡态E0的稳定性.
定理1若R0<1,则模型(3)的无病平衡态E0是局部渐近稳定的; 若R0>1,则不稳定.
证明由式(10)可知,
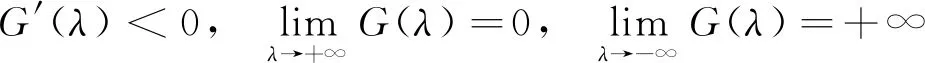
则特征方程(10)存在唯一实根.如果R0<1,即G(0)<1,那么G(λ)=1存在唯一的负实根λ*.进一步考虑方程(10)的复根.设λ=x+iy是G(λ)=1的任意复根,则
G(λ*)=1=|G(x+iy)|≤G(x)
由于G(λ)是关于λ单调递减的函数,所以Re(λ)=x≤λ*,即方程(10)的所有复根都具有负实部.因此,当R0<1时,模型(3)的无病平衡态E0是局部渐近稳定的.另一方面,如果R0>1,即G(0)>1,那么方程(10)存在唯一的正实根,从而无病平衡态E0是不稳定的.
定理2若R0<1,则模型(3)的无病平衡态E0是全局渐近稳定的.
证明令f(t,a)=(λ1(t,a)+λ2(t,a))s(t,a),由于s(t,a)≤1,故
f(t,a)≤λ1(t,a)+λ2(t,a)=k(a)V(t)
沿着特征线对模型(3)积分(当a (11) 将式(11)中的i(t,a)代入p(t,a)得 (12) 由式(11)中的i(t,a)和式(12)可得 (13) 记常数M为 则F(a)≤k(a)M.因此, 关于模型(3)地方病平衡态的存在性与稳定性,有下面的结论. 定理3当R0>1时,模型(3)存在唯一的地方病平衡态E*(s*(a),i*(a),r*(a),p*(a)). 证明模型(3)的平衡态必须满足如下与时间无关的常微分方程组: (14) 式中 (15) 根据模型(14)可得 (16) 将式(16)中的s*(a)代入i*(a)得 (17) 将式(17)代入式(16)中的p*(a)得 (18) 将式(17)和式(18)代入式(15),并将得到的方程左右两端同时除以V*(V*≠0),则 (19) 令V*=0,则 由于s*(a)+i*(a)+r*(a)=1,且s*(a)>0,所以i*(a)<1.又因为p*(a) H(β(1+K)N)<1 由于H(V*)是关于V*单调递减的函数,并且当R0>1时,有H(0)>1.因此,方程(19)在(0,β(1+K)N)上存在唯一实根.即,当R0>1时,模型(3)存在唯一的地方病平衡态. 讨论地方病平衡态的稳定性,将模型(3)在地方病平衡态E*处线性化,并考虑指数形式的解 则 (20) 式中 (21) (22) 利用常数变易法求解模型(21)得 (23) 把式(23)中的y(a)代入u(a)得 (24) 根据J(ω)的表达式,把式(23)中的x(a)和y(a)以及式(24)代入式(22)可得 (25) 式中 命题1假设ψ(a,τ)>0,∀0≤τ≤σ≤a,则 1)J(ω)是关于ω单调递减的函数,并且 2)J(0)<1. 证明根据式(25)和ψ(a,τ)>0可知: J(ω)≥0,J′(ω)<0 在式(25)中,令ω=0,则 (26) 由式(19)可知,式(26)的第一项等于1,所以J(0)<1. 定理4若R0>1,ψ(a,τ)>0,∀0≤τ≤σ≤a,则模型(3)的地方病平衡态是局部渐近稳定的. 证明类似于定理1的证明.若R0>1,ψ(a,τ)>0,则J(ω)=1存在唯一的负实根,并且所有复根都具有负实部.因此,当R0>1时,模型(3)的地方病平衡态是局部渐近稳定的. 迄今为止,已经发展了许多数值方法来逼近偏微分方程组的解.利用有限差分法沿特征线离散化模型(1),并进行数值模拟.假设模型基本参数如下: γ(a)=0.48sin2(0.1πa) θ(a)=0.26sin2(0.1πa) δ(a)=0.15sin2(0.1πa) ξ(a)=0.5×10-3sin2(0.1πa) 讨论模型的主要参数对基本再生数R0的影响,选择参数k(a)=0.2e-0.01a,β1(a)=0.000 11e-0.04a,β2(a)=0.075e-0.02a.根据R0的表达式,R0与接触率k(a)和传染率βj(a) (j=1,2)是正相关的.这也正如图1a所示,R0随着k(a)和β1(a)的增加而增加.此外,图1b表明,当k(a)固定时,可以通过降低β1(a)来降低R0.因此,适当减少接触并降低传染率是控制霍乱传播的有效措施之一. 图1 R0关于k(a)和β1(a)的敏感性 选择参数k(a)=0.9e-2a,β1(a)=0.000 11e-2a,β2(a)=0.075e-a,则计算可知R0≈0.402 1<1.根据定理2,无病平衡态E0是全局渐近稳定的.此时,易感者和感染者的密度分布如图2所示.特别地,当a=20时,对于不同的初值,S(t,20)随着t趋于无穷而趋于1,I(t,20)随着t趋于无穷而趋于0.这意味着,无论霍乱暴发的初始状态如何,最终都会灭绝. 图2 无病平衡态的稳定性,R0<1 选择参数k(a)=0.9e-a,β1(a)=0.000 11e-0.6a,β2(a)=0.075e-0.4a,则基本再生数R0≈1.426>1.由定理3可知,模型存在唯一的地方病平衡态E*.图3表明,地方病平衡态E*是局部渐近稳定的,当a=20时,对于不同的初值,I(t,20)随着t趋于无穷而趋于地方病平衡态.类似的,当t趋于无穷时,S(t,a),R(t,a),P(t,a)的密度分布会趋于地方病平衡态.这意味着,霍乱将持续存在. 图3 地方病平衡态E*的稳定性,R0>1 基于霍乱弧菌传播方式的多样性和种群的异质性,提出了一类具有生理年龄和环境传播的霍乱弧菌在人和人之间,人与环境之间传播的动力学模型,这里环境中霍乱弧菌也引入了年龄结构以刻画脱落的霍乱弧菌的活性.进一步利用半群理论,线性近似,比较原理等方法,获得了模型全局正解的存在性与唯一性,以及疾病基本再生数的精确表达式,证明了当基本再生数小于1时,无病平衡态是全局渐近稳定的; 而当基本再生数大于1时,无病平衡态是不稳定的,模型存在唯一的地方病平衡态,并在特定条件下得到其渐近稳定性.如何得到不带附加条件的地方病平衡态的局部或全局渐近稳定性,是进一步值得考虑的问题.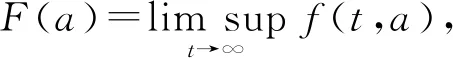
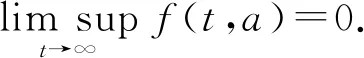

3 地方病平衡态的存在性与稳定性



4 数值模拟
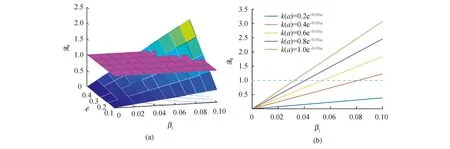

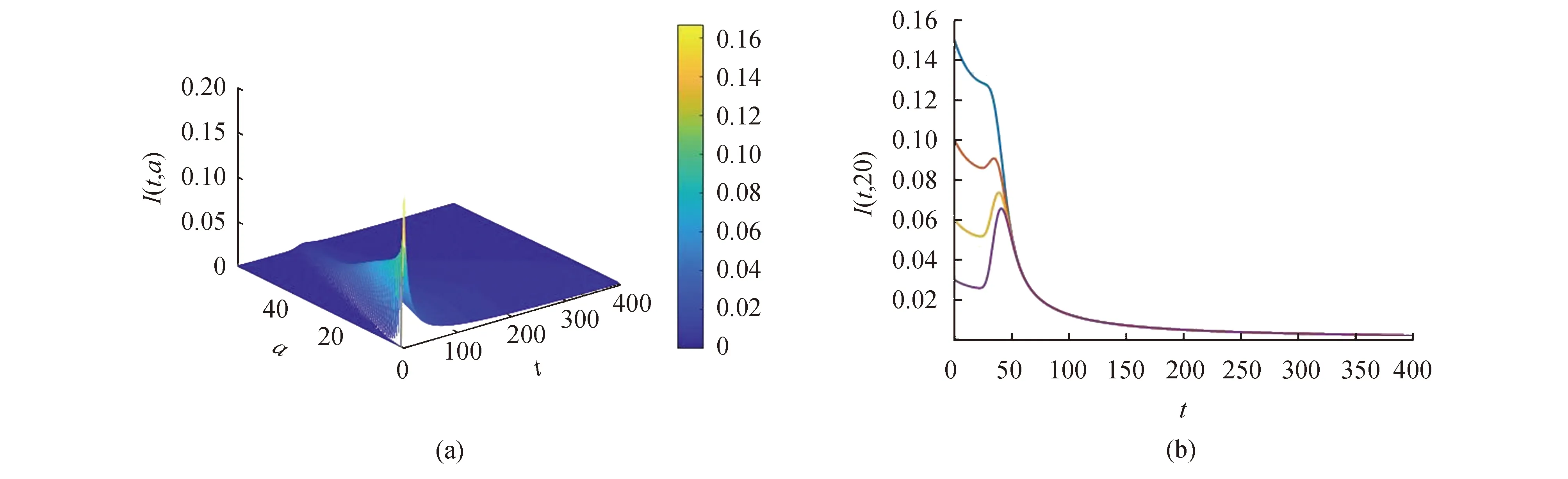
5 结论
