例谈分类讨论思想在动态几何问题中的应用
2023-05-05江苏省扬州市扬州大学225002
江苏省扬州市扬州大学(225002) 衡 晨
前不久刚颁布的《义务教育数学课程标准(2022年版》指出“图形与几何”模块在初中学段的主题包括图形的性质、图形的变化、图形与坐标,明确将“图形的变化”作为初中几何教学的重要主题[1].由此可见,初中阶段开始强调让图形“动”起来,不仅要求学生顺利求解动态几何问题,而且通过“动”起来的图形提高抽象能力、推理能力、几何直观等十大能力.
动态几何问题是一类综合性较强的题目,将数学的基础知识和基本技能完美结合,全面考查了学生应用理论知识的能力和解决实际问题的能力.不仅如此,动态几何问题的解决需要学生综合运用所学习的所有知识,运用数形结合、分类讨论、逻辑推理和数学模型的思想,从各个方面考查学生所具备的数学核心素养.从动态几何问题考查的知识点可将动态几何问题分为函数型、最值型、面积型、判断型等四大类[2].
本文主要论述函数型与判断型两类问题,函数型问题是指在动点运动过程中,对随之产生的函数关系进行探究的一类问题;判断型问题常常是探究运动过程中一些特殊位置或特殊图形是否存在的问题.本文中将判断型问题分为相似三角形和平行四边形进行讨论.解决动态几何问题的关键—明确不变量,发现不变关系,将变量用不变量表示,明确数量关系.
1 函数型
1.1 求解函数解析式及辨别函数图像
函数思想贯穿中学数学始终,在初中学习的主要有一次函数、二次函数、反比例函数,掌握它们的一般形式以及他们的图像与性质.对于和动点相结合的函数问题,一般而言,通过观察我们可以判断它是否为分段函数,若为分段函数则需要分类讨论,其自变量取值范围尤其重要.基于图形存在的变量构建函数关系,以动态的眼光观察变量之间的联系,从而解决动态几何问题.通过函数相关问题,着重培养学生的模型思想,具有模型意识.
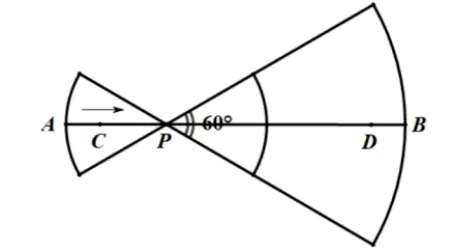
图1
例1如图1所示,线段AB=10,点C、D在AB上,AC=BD=1.已知点P从点C出发,以每秒1个单位长度的速度沿着AB向点D移动,到达点D后停止移动.在点P移动过程中作如下操作:先以点P为圆心,PA、PB的长为半径分别作两个圆心角均为60◦的扇形,再将两个扇形分别围成两个圆锥的侧面.设点P的移动时间为t(秒),两个圆锥的底面面积之和为S,则S关于t的函数图像大致是( ).
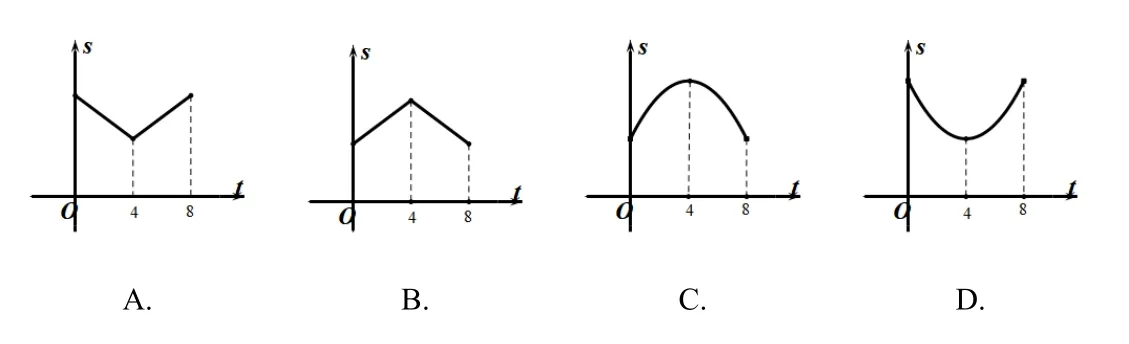
分析若想得到正确的函数图像,首先找出S与t的函数关系式,圆锥底面积S和底面半径有关;其次寻找底面半径和t的关系,用含t的代数式表示出两个扇形的半径,根据扇形的弧长等于底面周长可求出两个圆锥的底面半径;最后,根据扇形面积公式,求出S与t的函数关系式,根据函数关系选择相应的图像.
解析因为AB=10,AC=BD=1,所以CD=8,又因为PC=t,所以PA=t+1,PB=10−(t+1)=9−t.设两圆锥的底面半径分别为r和R,则:解得:所以,两个圆锥的底面面积之和为:
根据函数关系式可以发现该函数图像是一个开口向上的二次函数,故选D.
评析本题解题关键在于找到圆锥的底面半径,主要考查扇形弧长与圆锥底面周长之间的互化.对于有关函数图像的选择题,我们可以从选项中的“转折点”反推点的运动位置.例如,在本题中t=4就是一个“转折点”——动点所在的特殊位置,此时反推点P的运动位置,此时点P位于线段AB的中点.
例2如图2所示,⊙O的半径为1,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发(P点与O点不重合),沿O−>C−>D的路线运动,设AP=x,sin∠APB=y,那么y与x之间的关系图像大致是( ).
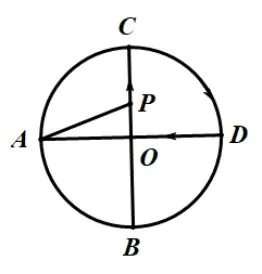
图2
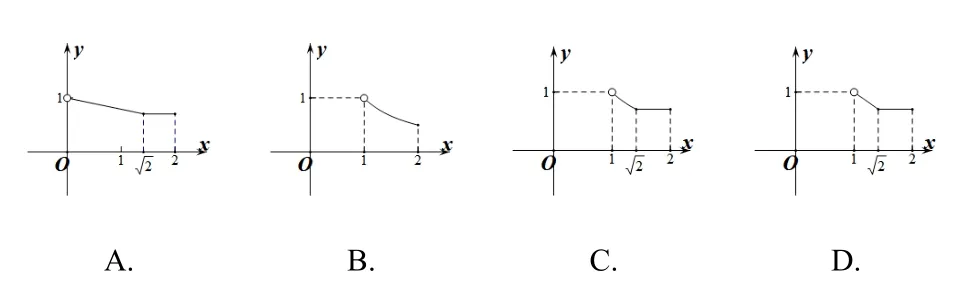
分析对于选择题来说,首先可以观察选项,发现选项中的函数图像中含有“转折点”,要联想到分类讨论的思想方法,其次认真分析题目,寻找具体的“转折点”,找到分段函数的解析式.
解析
(2)9个样品中Cd地累积指数值介于1.90~2.82之间,U地累积指数值介于0.81~1.46之间。其他元素地累积指数均<0。对于Cd元素,9个样品中有1个样品为轻度污染,8个样品为中度污染。对于U元素,9个样品中有4个样品为轻微污染,5个样品为轻度污染。
1)当P在CD上运动时,在RT∆AOP中,y=sin∠APB=
通过所求分段函数解析式得到,第一段为反比例函数,第二段为常函数,故选C.
2 判断型
2.1 相似三角形
相似三角形是中考中的高频考点,主要结合单动点以及双动点几何问题综合考察.对于相似三角形在解题时主要应用判定定理中的(SAS),从某一特定角出发,对其邻边进行分类讨论,在这个过程中,培养学生初步的抽象能力、更加理性的几何直观和空间想象能力.
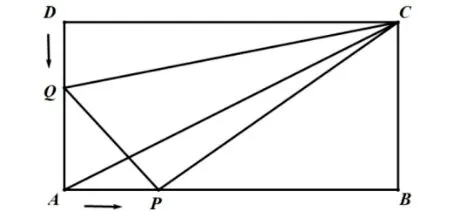
图3
例3如图3所示,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动,如果P和Q同时出发,用t(s)表示移动的时间(0 分析相似三角形的性质为对应边成比例,对应角相等.在解决该类问题时,从某一特定角出发,进行分类讨论.将所需线段用t表示出来,根据对应边成比例解得t的值. 解析根据题意可分为两种情况讨论: 综上所述,当t=1.2(s)或t=3(s)时,以点Q,A,P为顶点的三角形和∆ABC相似. 评析在本题中以点Q,A,P为顶点的三角形和∆ABC都含有一个直角,最简单的方法即从直角出发,对两条直角边进行分类讨论.那么,我们就可以选择对两条直角边分类讨论. 平行四边形这一节是初中的一个重要分水岭,对学生的抽象能力、空间观念、几何直观要求较高.关于动点和平行四边形存在性问题,主要结合平面直角坐标系进行考察,在该过程中,感悟数形结合的思想,会用数形结合的方法分析和解决问题.学会从几何的角度分析问题、解决问题,培养应用意识和创新意识,提升几何直观、空间观念、抽象能力、推理能力等. 关于动点和平行四边形存在性问题,常见题目的表述方式为:已知三个点A,B,C的坐标(如图4),若四边形ABCD是平行四边形,求点D的坐标.具体方法是:连接A,B,C三点,构成三角形,过A,B,C的每一个顶点画对边的平行线,三条直线两两相交,得到三个点D,不重不漏,一步到位[3].具体实施如下:按B−>C的方向,平移点A,得到点D1;按C−>B的方向,平移点A,得到点D2;按A−>B的方向,平移点C,得到点D3.具体操作如图5所示: 图4 图5 图6 例4如图6,直线+6与坐标轴分别交于A,B两点,动点P,Q同时从点O出发,同时到达点A,运动停止.点Q沿线段OA运动,速度为每秒一个单位长度,点P沿路线O−>B−>A运动. (1)直接写出A,B两点坐标; (2)设点Q的运动时间为t秒,∆OPQ的面积为S,求出S与t之间的函数关系式; (4)∆ABO与∆OPQ在运动过程中能否相似,若存在求出对应的t的值,若不存在,说明理由. 分析第(2)问的关键点在于对点P的运动轨迹进行分类讨论,从而得到S与t的分段函数;第(3)问依赖于第二问的函数关系式,根据条件求得P,Q坐标,第四个顶点的坐标,具体方法见解答过程;第(4)问有关三角形相似问题,同样需要对点P的运动轨迹进行分类讨论,在此基础上选择某一角,从该角邻边对应成比例进行讨论. 解析(1)A(8,0),B(0,6); (2)因为OA=8,OB=6,由勾股定理得AB=10.因为动点P,Q同时从点O出发,同时到达A点,点Q速度为每秒一个单位长度,所以点P的运动速度为=2; ①点P在线段OB上运动时,OP=2t,OQ=t,S=t2(0 图7 图8 (4)对点P运动轨迹进行讨论: 评析本题是一道非常经典的动态几何问题,难点主要在于多次分类讨论,考察的知识面较广,综合性较强.既考察了分段函数解析式,也考察了平行四边形第四点存在性问题以及三角形相似.在平时学习生活中多积累分类讨论的数学活动经验,这个题目难度会大大降低. 动态几何问题通常将函数和图形的相关性质结合考察,将几何和代数相结合.由以上例题可知,动态几何问题的解析过程中,最重要的是分类讨论的数学思想,寻找动点的特殊位置.在不同的问题情境中,关键在于用“不变量”表示“变量”,“以静制动”,要抓住问题本质,适当简化问题模型,找出题目中静与动的主体,可适当构造辅助线[4].动态几何问题对于提升学生灵活运用知识的能力、加强知识间的相互转换与联想有重大作用.分类讨论地数学思想方法有利于加强学生思维的条理性、缜密性.
2.2 平行四边形存在性问题
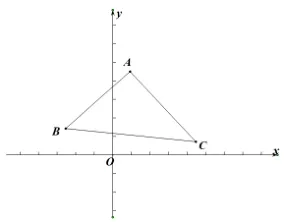
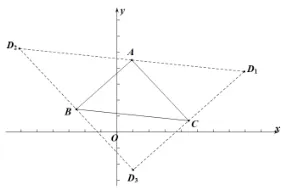
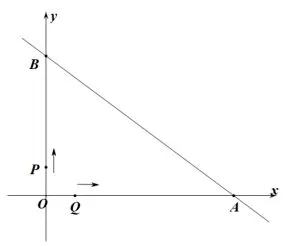




3 总结
