基于改进AHP法和CRITIC法耦合赋权的松散承压含水层富水性评价

葛如涛, 陈陆望, 王迎新, 张 杰, 李蕊瑞

(合肥工业大学 资源与环境工程学院,安徽 合肥 230009)

我国华北隐伏型煤田第四系松散承压含水层覆盖于煤系地层之上,是煤矿顶板水害防治、地下水资源管理与生态环境保护等研究的热点。该类含水层以非胶结砂土、砂砾为骨架,砂泥互层明显,具有承压性,富水性空间展布差异性较大;此外,受煤矿区长期采动影响,含水层富水性的动态变化明显[1-2]。目前,对于松散承压含水层富水性评价与分区,研究方法可分为以下2类:① 以《煤矿防治水细则》为代表,根据水文地质勘探成果,采用抽水试验得到的单位涌水量作为标准评价指标进行含水层富水性评价与分区[3];② 通过物探手段进行探测,包括直流电法、瞬变电磁法、高密度电法等[4]。物探手段的解译成果受研究人员经验和技术水平影响,存在多解性;采用单位涌水量进行富水性分区,由于抽水试验成本高、过程复杂,抽水试验钻孔数量与抽水试验次数有限,无法反映采动影响下含水层富水性的时空动态变化。

为了提高松散承压含水层富水性评价与分区的准确性与普适性,文献[5-6]借助地理信息系统(geographic information system,GIS)的空间信息融合功能,运用沉积控水规律建立多因素复合评价模型;文献[7]基于层次分析(Analytic Hierarchy Process,AHP)法,借助GIS空间分析功能,开展多元信息融合,对松散承压含水层的富水性进行分析与评价。采用多因素复合法,关键在于如何合理确定各影响因素的权重。采用AHP法或者改进AHP法对主控因素进行赋权[8-9],属于主观赋权法,主观性较强,存在局限性。文献[10]在研究含水层非均质性问题时采用熵权法对主控因素进行赋权,但该方法在赋权时未考虑专家意见;文献[11]在研究风化基岩富水性评价方法时,分别使用AHP法、熵权法及耦合两者的方法来确定影响因素权重,结果表明,耦合AHP法和熵权法确定权重进而预测的富水性类别,与实测数据吻合度明显高于单独使用某一赋权法。而熵权法仅根据各影响因素本身变异大小确定其权重,未考虑影响因素之间的冲突性;基于指标相关性的指标权重确定(CRiteria Importance Through Intercriteria Correlation,CRITIC)法兼顾影响因素变异大小和冲突性,在赋权准确程度方面优于熵权法[12]。因此,耦合改进AHP法与CRITIC法的赋权方法会使评价结果更为合理。

本文以淮北煤田松散承压含水层为研究区,将改进AHP法和CRITIC法进行耦合,来确定第四系松散承压含水层富水性影响因素的权重,提出一种更科学的、多因素复合的松散承压含水层富水性评价模型。该模型所需参数均可通过普通地质勘探孔数据获得,无需进行更多的抽水试验,降低了抽水钻孔的施工成本和时间投入;相比于仅使用矿区为数不多的抽水试验孔数据进行含水层富水性评价与分区,该模型评价准确度更高。此外,由于含水层水位受采动影响,发生永久性或半永久性变化,以致含水层富水性产生相应变化,该富水性评价模型能够较准确地对研究区富水性进行时空动态评价。

1 研究区地质背景

淮北煤田地处华北板块,位于华北平原南部、郯庐断裂带西侧;区内除灵璧、泗县、濉溪、涡阳等地有新元古界和下古生界基岩出露外,其余绝大部分地区为厚度180～400 m的第四系松散层所覆盖[13-14];煤田所在区域属于暖温带半湿润性气候,年均降水量为700～950 mm,年降雨量最大为1 107 mm;第四系松散层除直接接受大气降水补给外,还受到地表水体的渗流补给;煤田地表水系发育,沱河、淝河、新汴河、浍河、濉河等河流呈不对称羽状展布于淮河北岸,对浅部松散层起到丰蓄枯补的作用[15]。淮北煤田松散层自上而下可划分为4个含水层(组)及3个隔水层(组),第一含水层(简称 “一含”)为近地表的潜水孔隙含水层,第二、三、四含水层(简称“二含”、“三含”、“四含”)为孔隙承压含水层[16]。其中,四含直接覆盖在煤系地层之上,是矿井开采的直接充水水源。含水层多为黏土质砂、粉细砂和中砂交替沉积,一般单层厚度较小,多为0.3～3.5 m。含水层内含有黏土夹层。隔水层多由钙质黏土与砂质黏土组成,第一、二隔水层厚度较小,普遍小于25 m,隔水性能一般;第三隔水层厚度大,平均厚度达80 m,隔水性能强。

2 富水性评价模型的建立

2.1 影响因素确定

影响松散承压含水层富水性的因素是多元的。本文通过收集淮北煤田青东煤矿、朱仙庄煤矿、祁南煤矿、祁东煤矿相关水文地质资料,分析上述4个煤矿松散承压含水层抽水试验60个有效钻孔的数据,发现其富水性主要受补给情况、含水层厚度、岩性及砂泥分布情况控制。其中,岩性为定性指标,故先按类别对其量化,然后用级配系数来定量表示岩性特征。最终选取隔水系数R、水头系数G、含水层厚度S、最厚砂层厚度M、级配系数D、砂泥互层系数P共6个影响因素。

(1) 隔水系数R。松散承压含水层富水性与地表水体、大气降水直接或间接补给有关,含水层埋深越浅,接受的补给越充分。隔水层的存在使得隔水层下伏含水层接受的补给受到抑制,其抑制程度与上覆隔水层厚度相关。将松散层某一层位含水层的上覆隔水层累加厚度与该层位含水层底板埋深的比值定义为隔水系数R,即

(1)

其中:r为上覆隔水层总厚度;H为该含水层底板埋深。R越大,该含水层接受补给越困难。

(2)水头系数G。承压水头的变化能够反映含水层承压水位的变化,将某一层位含水层承压水头T与该含水层顶板埋深H0的比值定义为水头系数G,即

(2)

G越大,说明单位厚度的含水层给水能力越强,与地表的水力联系越强。

(3) 含水层厚度S。S是影响含水层富水性强弱的重要因素,地下水赋存情况与S密切相关,在其他影响因素相差不大的情况下,S越大,含水层富水性越强。

(4) 最厚砂层厚度M。M是指某一含水层内厚度最大的一层砂砾层的厚度,只要没有黏土夹层,可以是不同粒径砂砾层累加厚度。在S一定的条件下,M越大,说明层内黏土层越薄、层数越少,则含水层储水空间越大,层内水力联系越强,富水性越强。在S及其他影响因素相差不大的情况下,M与富水性强弱相关。

(5) 级配系数D。在其他影响因素一定的情况下,松散含水层土体粒径组合不同,其富水性不同。根据抽水试验成果可知,卵砾石层较砂砾层富水性强,粒径大的砂砾层较粒径小的富水性强。将土体粒径组合对含水层富水性的贡献大小进行量化,见表1所列,进而构建表征含水层富水性强弱的粒径组合系数,即级配系数D,D值越大,富水性越强。

D计算公式为:

D=∑dγcγ/S

(3)

其中:dγ为粒径类别的量化值;cγ为不同粒径土层的厚度;γ为土体粒径类别。

表1 松散层按土体粒径级别赋值结果

(6) 砂泥互层系数P。P是在砂泥比基础上进行改进的评价指标。以往研究采用的砂泥比仅简单计算含水层内砂砾层与黏土层累计厚度的比值,而未考虑垂向砂泥互层分布对含水层富水性的影响。钻探成果显示,淮北煤田内各级松散承压含水层在垂向上一般都为多层结构,具体表现为砂砾层与黏土层交互沉积,故将这样的一组上覆砂砾层及其下伏黏土层定义为一个砂泥互层。在含水层厚度相近时,互层层数越多,单个互层内黏土比率越大,意味着层内砂砾层之间的水力联系越差,富水性相应较弱;反之,富水性较强。

朱仙庄煤矿8105-四含检2孔与青东煤矿2015-水1孔2个抽水钻孔揭露的四含厚度与砂泥比均相差无几。前者有2个互层,作为隔水层的黏土层将砂层分割开,砂层之间水力联系受阻;而后者仅有1个互层,为单一砂层含水层。2个钻孔抽水试验得到的单位涌水量q分别为2.8×10-5、0.01 L/(s·m),验证了上述观点。依据各个互层中黏土厚度比率对富水效果的贡献大小将其量化,构建表征砂泥互层影响富水性强弱的砂泥互层系数P,P值越大,层内水力联系越弱,富水性越弱。P计算公式为:

P=∑pεlε/S

(4)

其中:pε为互层内黏土厚度所占比率的赋值;lε为各个互层的厚度;ε为各互层序号。

pε赋值见表2所列。

表2 单个互层内黏土厚度比率级别赋值结果

淮北煤田青东、朱仙庄、祁南、祁东4个煤矿松散承压含水层60个抽水试验有效钻孔及其层位见表3所列,对应60个钻孔的6个影响因素取值见表4所列。

表3 淮北煤田抽水试验60个钻孔名称及其层位

2.2 权重确定

2.2.1 改进AHP法的赋权方法

传统的AHP法在构造判断矩阵时,各指标之间相对重要程度的判断会受到该领域专家研究方向、工作经验等影响,具有一定的主观性;此外,该方法固化了标度,不具有扩展性和传递性,导致矩阵表述与实际情况相差很大[17]。改进AHP法的赋权方法如下:

(1) 采用极大值法和极小值法对影响因素进行归一化处理,消除影响因素单位不同对数据比较造成的影响。极大值法适用于与评价结果成正比的影响因素数据归一化,极小值法适用于与评价结果成反比的影响因素数据归一化。极大与极小值法计算公式分别为:

(5)

(6)

其中:Xi为第i个影响因素数据归一化后的量化值;i为影响因素序号;maxxi、minxi分别为第i个影响因素数据归一化前的最大值和最小值。

(2) 运用SPSS软件中的CORREL函数分别对各影响因素和评价标准值(钻孔的单位涌水量q)进行相关性分析[18],计算出各影响因素与评价标准值的相关系数,相关系数越大,表明该因素与评价标准值拟合得越好,则该因素相对重要程度越高。采用期望标度法,根据重要程度的传递性法则将各因素两两比较排序,依次可以计算出判断矩阵未知元素的值。

期望标度取值见表5所列。

表5 期望标度取值

(3) 计算各影响因素的样本标准差s(i)(i=1,2,…,n)。样本标准差越大,说明该因素内部变化形式越丰富,其对于综合评价的影响越大。因此,可采用各影响因素的样本标准差来表征各影响因素对富水性的影响程度,从而构建判断矩阵B1-2。B1-2中元素计算公式为:

(7)

其中:s(i)、s(j)分别为影响因素i和影响因素j的样本标准差;smax、smin分别为影响因素样本标准差的最大值和最小值;bmin为相对重要程度参数,bmin=min{9,int[smax/smin+0.5]},int为取整函数。

(4) 由于多阶判断矩阵较为复杂,矩阵中会出现某些元素前后矛盾的现象,有必要检验判断矩阵的一致性,保证输出结果及最终权重向量的准确性。一致性指标(consistency index,CI)IC检验公式为:

IC=(λmax-n)/(n-1)

(8)

IR=IC/RC

(9)

其中:λmax为判断矩阵的最大特征值;RC为随机一致性比率(consistency rate,CR);IR为随机一致性指标(random index,RI)。当CR小于0.1时,可认为判断矩阵满足一致性要求,反之,需要调整判断矩阵。对于六阶矩阵,对应的随机一致性指标RI[19]为1.24。

(5) 求出各个判断矩阵的最大特征值及其对应的特征向量,标准化处理后可得所求的权重向量W1-1、W1-2。若各判断矩阵符合一致性检验要求,则综合评价矩阵是可行的。故可取各权重向量组成元素ei的平均值,构建结合矩阵B1-1、B1-2的权重向量W1为:

(10)

改进AHP法具体实现过程如下:

(1) 由2.1节可知,R、P与富水性近似呈负相关性,G、S、M、D与富水性近似呈正相关性。采用对应的归一化方法((5)式、(6)式)对表4影响因素数据进行归一化处理。

(2) 分别对各影响因素和评价标准值进行相关性分析,得出各影响因素与评价标准值之间的相关系数,6个影响因素按相关系数从大到小排序依次为:R(0.645)、M(0.492)、P(0.386)、S(0.374)、D(0.344)、G(0.271)。采用期望标度法构建判断矩阵B1-1为:

B1-1=

(3) 计算得到影响因素样本标准差,6个影响因素按其样本标准差从大到小排序依次为:P(0.283)、M(0.253)、S(0.236)、D(0.216)、R(0.188)、G(0.174)。经计算,bmin=min{9,int[2.118]}=2。根据(7)式构建判断矩阵B1-2为:

B1-2=

(4) 判断矩阵B1-1、B1-2均为六阶矩阵,经计算其最大特征值λmax分别为6.000 1、6.002 2;通过(8)式、(9)式可得CR1-1为2.0×10-5,小于0.1;CR1-2为3.8×10-4,小于0.1。因此,判断矩阵B1-1、B1-2均满足一致性检验要求。

(5) 求出各判断矩阵对应最大特征值的特征向量,标准化处理后得到所求权重向量。B1-1对应的影响因素权重W1-1中6个影响因素的权重分别为:R,0.349 4;G,0.071 9;S,0.121 6;M,0.205 5;D,0.093 5;P,0.158 1。B1-2对应的影响因素权重W1-2中6个影响因素的权重分别为:R,0.168 2;G,0.111 7;S,0.227 6;M,0.214 9;D,0.161 3;P,0.116 2。

B1-1、B1-2均满足一致性检验要求,故可用(10)式求得最终R、G、S、M、D、P6个影响因素权重,进而得到权重向量W1,即W1=[0.258 8 0.091 8 0.174 6 0.210 2 0.127 4 0.137 2]。

2.2.2CRITIC赋权方法

CRITIC法是文献[20]提出的一种基于客观条件的赋权方法。该方法主要根据各指标的信息量和相关性对其赋权,分别用对比强度和指标冲突性来反映各指标的信息量和相关性。对比强度以各指标内部变异大小来衡量,可以通过标准差来反映变异大小;标准差越大,该指标反映的信息量越大,其权重相应较大。指标冲突性反映指标之间的相关性特征,通过计算各指标相互之间的相关系数来表示;两个指标的相关系数越大,其正相关性越强,则这两个指标冲突性较低。CRITIC法不仅考虑影响因素变异程度对权重的影响,还考虑各因素之间的冲突性特征,而熵权法仅考虑到前者,因此CRITIC法在综合评价效果上要优于熵权法[12]。因素两两之间的Pearson相关系数ρ、各因素的标准差σ计算公式分别为:

(11)

(12)

设Ej为第j个影响因素所包含的信息量,Ej越大,该因素相对重要程度越高,由此可以计算出第j个因素的客观权重wj,进而可求出权重向量W2=[w1w2…wn]。Ej、wj计算公式为:

(13)

(14)

CRITIC法具体实现过程如下:

(1) 与改进AHP法相同,首先用(5)式、(6)式对影响因素的数据进行归一化处理,消除由于影响因素单位不同造成的影响,然后用(12)式计算得到6个影响因素内部的标准差分别为:P,0.283 2;M,0.253 3;S,0.236 2;D,0.216 4;G,0.187 6;R,0.173 6。

(2) 利用SPSS软件,通过(11)式计算得到影响因素两两之间的Pearson相关系数,见表6所列。

(3) 根据(13)式、(14)式可得R、G、S、M、D、P6个影响因素权重,进而得到权重向量W2,即

W2=[0.171 3 0.187 2 0.157 3

0.125 9 0.171 7 0.186 5]。

表6 影响因素之间的Pearson相关系数

2.2.3 耦合赋权

为使建立的耦合赋权模型兼顾该领域专家的经验和实测数据的客观性特征,在改进AHP法赋权与CRITIC法赋权求出主、客观权重向量的基础上,基于总偏差最小化的原则,采用博弈论对改进AHP法和CRITIC法进行耦合,从而得到耦合赋权模型。

(1) 采用2种方法对各影响因素进行赋权,得到2组不同的权重数据。2个评价结果的随机性组合为:

(15)

其中:W为所有可能出现的权重数据组合向量;α1、α2为线性组合系数;W1、W2为采用某种赋权方法所获得的权重数据组合向量。

(2) 基于博弈论的权重集结本质,对线性组合系数α1、α2优化处理,据此建立决策模型。

(3) 根据矩阵的微分性质,计算求得(15)式的最优化一阶导数条件矩阵,即

(16)

(17)

(18)

(5) 获取最优化系数后,建立最优化权重耦合模型为:

(19)

2.2.4 含水层富水性评价模型的建立

多因素复合的松散承压含水层富水性评价流程如图1所示。

图1 松散承压含水层富水性评价的流程图

基于改进AHP法和CRITIC法耦合得到最终的权重向量W*,根据线性加权的方法建立淮北煤田多因素复合的松散承压含水层富水性评价模型为:

0.170 5f(S)+0.190 1f(M)+

0.138 0f(D)+0.148 9f(P)

(20)

其中:V为富水性综合指数,取值范围为0～1;Ai为各影响因素数据归一化后的数值;f(R)、f(G)、f(S)、f(M) 、f(D)、f(P)分别为R、G、S、M、D、P6个影响因素数据归一化后的数值。

聚类分析法能够从样本数据入手,在保证组间差异最大化、组内差异最小化的基础上恰当有效地进行分类。利用SPSS软件中的系统聚类分析法,对60个钻孔的富水性综合指数分级分类。由于淮北煤田松散层未发现极强富水性的抽水钻孔资料,将计算得到的富水性综合指数进行3级划分,结果如图2所示。

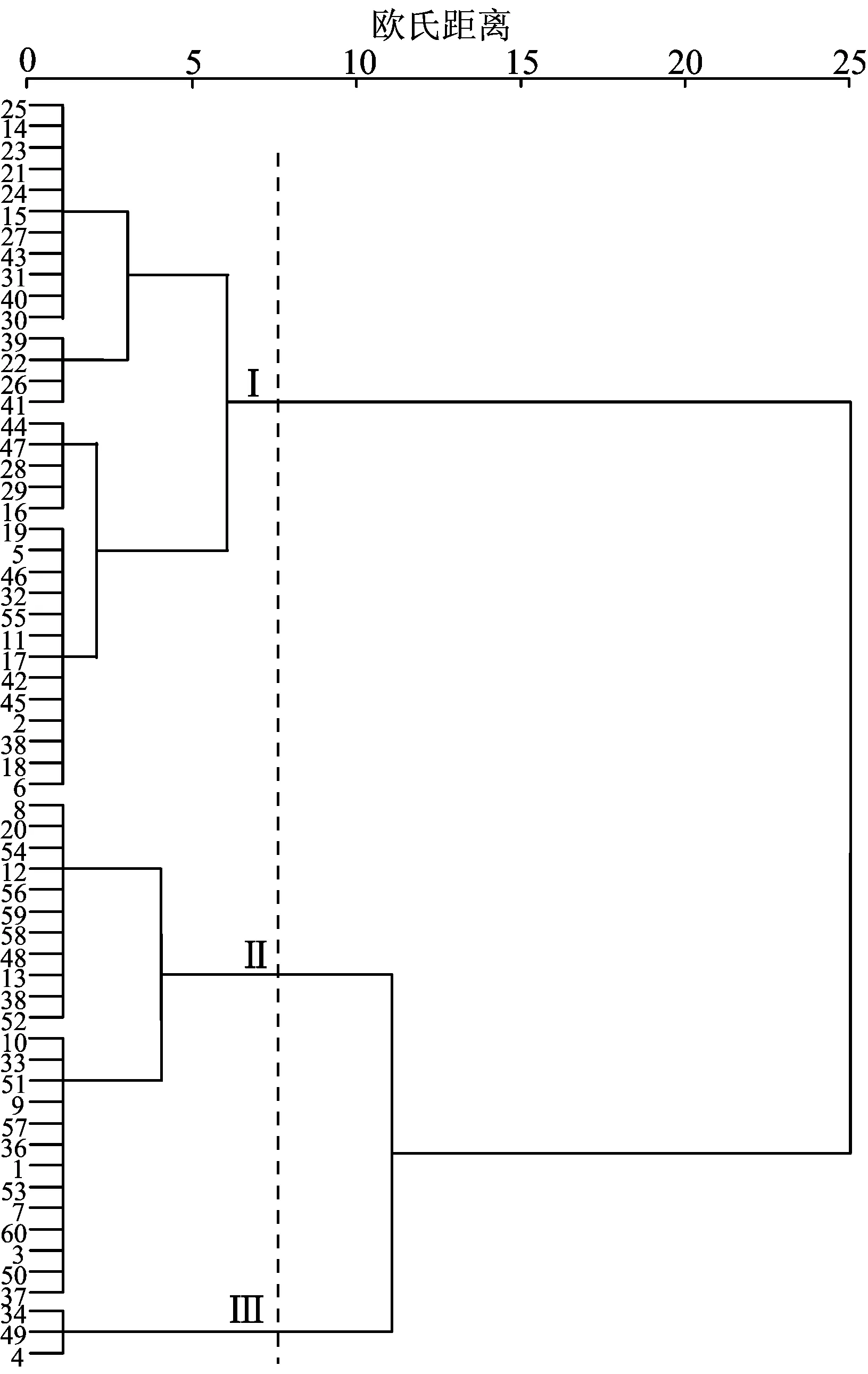
图2 淮北煤田松散承压含水层富水性综合指数聚类分析结果

通过欧氏距离7.5的点纵穿树状图画同型线,Ⅰ区对应弱富水性,Ⅱ区对应中等富水性,Ⅲ区对应强富水性。Ⅰ区、Ⅱ区与Ⅲ区之间的中断值见表7所列。

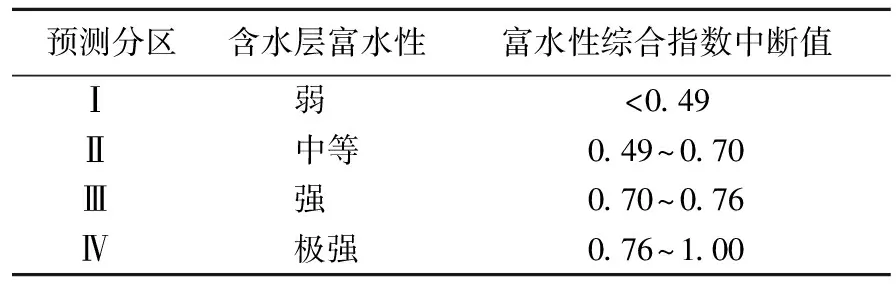
表7 淮北煤田松散承压含水层富水性评价分区中断值

表7中,遵循《煤矿防治水细则》[3]中的含水层富水性4级划分原则,选取研究区松散承压含水层抽水试验钻孔对应的富水性综合指数最大值作为划分强富水(Ⅲ区)和极强富水(Ⅳ区)的中断值。

3 富水性评价模型的验证

为了验证本文建立的多因素复合的松散承压含水层富水性评价模型的准确性,收集淮北煤田钱营孜煤矿、任楼煤矿、孙疃煤矿及卧龙湖煤矿相关数据,整理得到松散层有效抽水试验钻孔11个,采用11个钻孔的数据进行模型验证。首先根据(20)式计算11个钻孔数据的富水性综合指数,并根据中断值的大小进行分类,然后将该模型得到的含水层富水性与由钻孔抽水试验得到的富水性进行对比,验证结果见表8所列。11个钻孔数据中,8个弱富水层位均评价正确;对于3个中等富水层位,2个评价正确;评价不正确的钻孔为一含抽水试验孔。由于一含为近地表潜水或半承压含水层,其性质与承压含水层有所差别,因此,本文模型验证正确率达90.91%。表8中,单位涌水量q的单位为L/(s·m)。

表8 单位涌水量q富水性与模型评价结果对照

4 工程应用

4.1 资料收集与处理

选择朱仙庄煤矿北部采区,对其松散承压含水层四含进行富水性评价与分区。将63个普通地质钻孔柱状图与相关水文资料,按照不同影响因素整理出各自数据并归一化处理后,通过多因素复合的淮北煤田松散承压含水层富水性评价模型,计算出对应各个钻孔的富水性综合指数V。

4.2 富水性评价与动态预测

朱仙庄煤矿北部采区受采动影响,四含水位明显降低,其水位埋深及变动情况见表9所列。由表9可知,从2017年12月至2020年7月,四含水位平均下降36.75 m。

依据该含水层富水性综合指数V与中断值,得到朱仙庄煤矿北部采区四含富水性分区,如图3所示。对比图3a、图3b可以看出,朱仙庄煤矿北部采区受采动影响,中等富水区明显减小。根据抽水钻孔I-I-6在1964年7月的抽水试验,单位涌水量q为0.136 L/(s·m),该数据显示该区域为中等富水,根据2017年水位进行评价,该区域仍为中等富水,但根据2020年水位进行评价,该区域已变为弱富水。

表9 朱仙庄煤矿北部采区四含水位埋深及变动情况

图3 朱仙庄煤矿北部采区不同水位埋深下的四含富水性分区结果

5 结 论

(1) 选取隔水系数R、水头系数G、含水层厚度S、最厚砂层厚度M、级配系数D、砂泥互层系数P共6个影响因素作为评价指标,基于博弈论对改进AHP法和CRITIC法进行耦合,建立多因素复合的松散承压含水层富水性评价模型,建立的耦合赋权模型具有兼顾该领域专家经验和实测数据的客观性特征。

(2) 对该多因素复合的松散承压含水层富水性评价模型进行验证,评价结果正确率高达90.91%,所选评价指标均可通过普通地质勘探孔数据得到,无需过多开展现场抽水试验与相关物探工作,解决了由于抽水孔数量少导致分区结果不理想的问题,也降低了抽水孔的施工成本,避免了运用物探手段进行富水性评价时,解译成果受研究人员的经验和技术水平影响、有主观局限性、存在多解性等问题。

(3) 松散承压含水层的水位等水文地质条件受采动影响,会发生永久性或半永久性变化,以致含水层富水性也相应发生改变。通过该多因素复合的松散承压含水层富水性评价模型,可以对研究区富水性开展时空动态评价与预测。