磁热冲击下非均质圆筒的动态响应分析
2023-05-05吴辉阳詹春晓王美芹吴枝根
吴辉阳, 詹春晓, 王美芹, 吴枝根
(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
圆筒结构是工程实际中常见的一种结构形式,被广泛应用于多种工业领域,如航空航天、化工、石油等领域。圆筒结构在工程应用中经常受到机械冲击、热冲击、磁冲击等各类冲击作用。冲击载荷会在圆筒中引起较大的动应力峰值,导致结构因强度不足出现损伤。因此,研究冲击作用下圆筒结构的动态响应,探索缓解冲击影响的有效措施,对相关工程问题具有重要的理论指导意义。
关于圆筒和空心圆球的动态响应,近几十年来已有大量研究成果。文献[1]用Hankel变换和拉普拉斯变换得到空腔球体内的热动应力分布规律;文献[2]通过求解Navier方程给出功能梯度厚空心球一维稳态热应力和机械应力的解析解;文献[3-5]研究层合圆筒和功能梯度圆筒在多种载荷影响下的动态响应,借助Hankel变换和拉普拉斯变换给出它们的精确解;文献[6]采用级数方法求解运动方程,并在时域中应用快速拉普拉斯逆变换,对功能梯度圆柱在热冲击下动应力进行解析分析;文献[7]使用二阶配点法对受动态热、机械载荷的温变功能梯度圆筒进行非线性热应力分析;文献[8]用有限差分法和Newmark法,研究具有功能梯度层的双层空心圆柱受热、机械载荷的动态热弹性行为;文献[9]利用Lord-Shulman理论建立能量方程和运动方程,使用广义微分求积法、Newmark法和Picard逐次算法对方程进行求解,得到温度、位移和应力随时间变化的规律。近些年,关于磁冲击下圆筒结构动态响应的研究逐渐增多。文献[10]给出内层为功能梯度材料(functionally graded material,FGM)、外层为均质材料的双层圆筒磁热弹性行为的解析解;文献[11]通过求解控制方程得到压力、温变和磁场共同作用下,双层圆筒径向应力和环向应力的解析解;文献[12-13]利用有限Hankel变换和拉普拉斯变换,研究磁冲击下单层和双层均质软磁材料圆筒的动态响应,得到动态位移与应力的解析解。
关于磁热冲击下圆筒的动态响应分析,相关文献主要集中于均质圆筒或双层均质材料组合圆筒的研究,对非均质圆筒,如功能梯度圆筒、含功能梯度层的层合圆筒的动态位移和应力分析很少。本文研究材料性质沿径向任意梯度变化的非均质圆筒在磁热冲击作用下的动态响应,为了探索动应力峰值的影响因素,采用延迟热冲击、将双层均质圆筒结构中的内层或外层替换为功能梯度层等方式进行分析,给出降低动应力峰值的一些可行措施。
1 分析模型
受磁场和温度场作用的非均质圆筒如图1所示,该无限长弹性圆筒的内半径为a,外半径为b,材料性质沿径向任意梯度变化。圆筒受突变轴向磁场Hz(t)及温度场T(t)的冲击作用,磁热冲击下,该圆筒的动态响应属于轴对称平面应变问题。

图1 受磁场和温度场作用的非均质圆筒分析模型
轴对称平面应变问题的运动方程为:
(1)
其应力与位移关系[6,12]为:
(2)
(3)
其中:ur(r,t)为径向位移;σr(r,t)、σθ(r,t)分别为径向应力和环向应力;E、ν、ρ、α分别为圆筒材料的弹性模量、泊松比、质量密度和线膨胀系数;μ0为真空磁导率;Hz为磁场强度。
初始条件为:
σr(r,0)=0,σθ(r,0)=0
(4)
假设圆筒内、外表面不受面力作用,则边界条件为:
σr(a,t)=0,σr(b,t)=0
(5)
2 求解方法
由于材料性质沿径向变化的不确定性,圆筒的动态响应不可能从控制方程(1)~(3)式中得出解析解,需要将解析法与数值法相结合,对磁热冲击下的任意梯度圆筒进行动态分析。
由(2)式可得:
(6)
将(2)式、(3)式和(6)式代入(1)式,有
(7)
由(6)式与(7)式可构成偏微分方程组,其矩阵形式为:
(8)
其中:R为状态向量;G为系数矩阵;B为非齐次项矩阵。
R=[ur(r,t)σr(r,t)]T,

用时刻t0,t1,t2,…,tk,…将时间t划分成等间隔的时间段,t0为初始时刻;Δt为相邻两个时刻之间的间隔,即时间步长,Δt=tk-tk-1。根据Newmark法,tk时刻位移对时间的二阶偏导数可近似为:
(9)

(10)
(11)
具体分析时通常取参数ξ=1/4,ζ=1/2。
由于空心圆筒中的材料性质随r变化,将圆筒划分为N层圆柱壳,第i层圆柱壳的厚度为di(i=1,2,…,N),内、外半径分别记为ri-1、ri,因而ri=a+d1+…+di,r0=a,rN=b。在第i层圆柱壳的系数矩阵G和非齐次项矩阵B中,取r=hi=(ri+ri-1)/2,材料性质取该层圆柱壳中面处的参数值,则(8)式在每层圆柱壳中都成为一个常系数非齐次微分方程组,即状态方程。由(8)~(11)式得到tk时刻第i层圆柱壳的状态方程为:
(12)

其中,[gri(r,t)]k近似为[gr(ri,tk)+gr(ri-1,tk)]/2。对(12)式两边积分,可得:
[Ri(r,t)]k=Di(r-ri-1)[Ri(ri-1,t)]k+
[Hi(r,t)]k,
Di(r-ri-1)=exp[Gi(r-ri-1)],

(13)
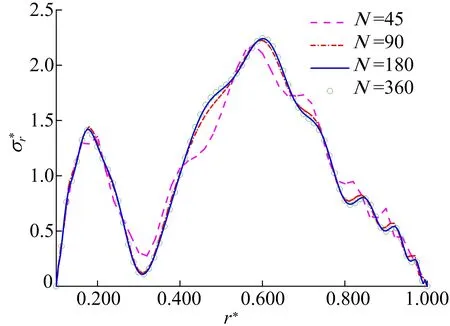
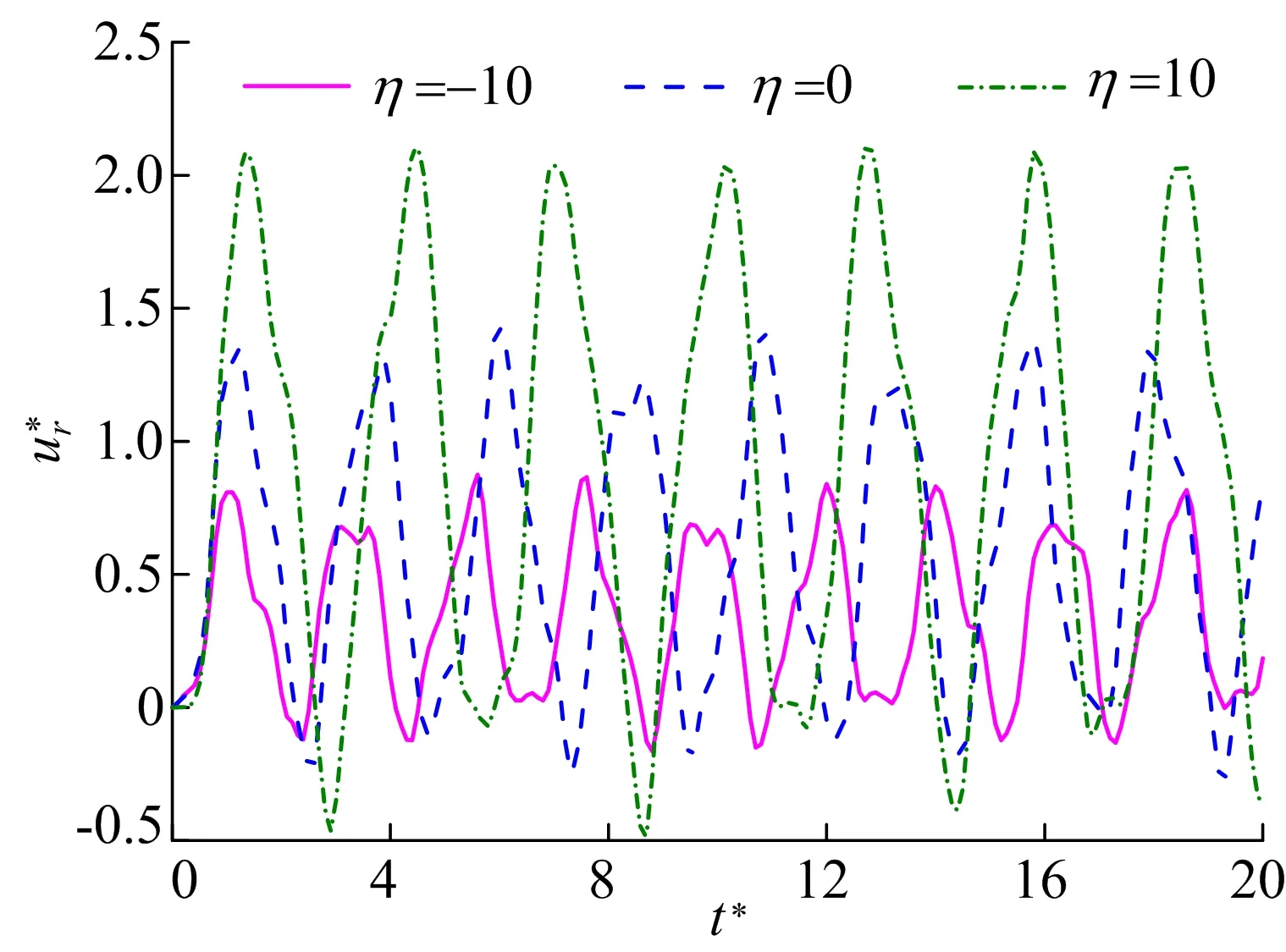
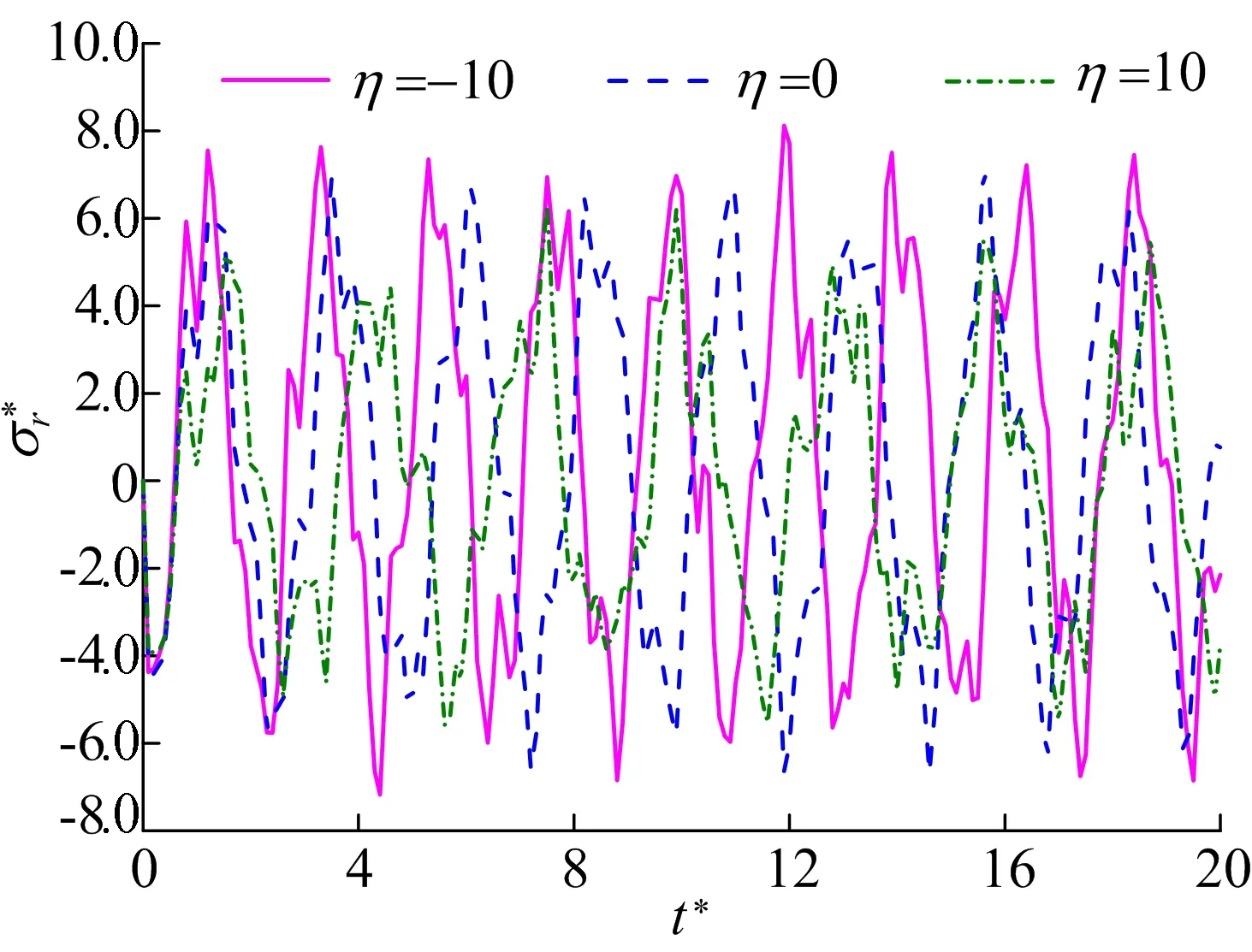
其中,ri-1 由(13)式和状态向量在层间的连续条件[Ri(ri-1,t)]k=[Ri-1(ri-1,t)]k,可以推导出tk时刻圆筒内、外表面处状态向量之间的关系为: (14) 在(14)式中应用边界条件(5)式,可以求得圆筒内、外表面处tk时刻的状态向量R1(r0,tk)和RN(rN,tk),再由(13)式进而可得tk时刻任意位置处的状态向量Ri(r,tk)。当N→∞且di→0时,N层圆柱壳构成的层合圆筒将无限趋近于原来的非均质圆筒。具体分析中,选择适当的圆筒分层数N和时间步长Δt,可以得到圆筒在任意时刻任意位置处足够精确的位移和应力分量。 本文求解方法给出了受磁热冲击作用的轴对称非均质无限长圆筒动态响应的半解析解,为检验本文解的正确性和有效性,分别对均质圆筒、双层均质圆筒及含FGM的层合圆筒进行分析。为方便结果分析与讨论,引入如下无量纲变换: (15) 其中:μ0=4π×10-7H/m;cL为弹性波的传播速度;E0、ρ0分别为弹性模量和质量密度参考值。 图2 不同N下沿r*的分布 图3 不同N下沿r*的分布 图4 r*=1.000处随t*的变化 从图4可以看出,由本文方法得出的位移与文献[12]的结果吻合良好。 图5 r*=0.775处随t*的变化 内层为氧化铝、外层为铝合金的双层圆筒,氧化铝分布区域为a≤r<(a+b)/2,铝合金分布区域为(a+b)/2≤r≤b,a=0.002 m,b=0.040 m。双层圆筒受磁热冲击作用,热冲击的发生与磁冲击有一定的时间延迟,磁场和温度场分别为: Hz(t*)=HzH(t*), (16) 图6 磁热冲击下双层圆筒中r*=0.275处随t*的变化 图7 磁热冲击下双层圆筒中r*=0.275处随t*的变化 为考察功能梯度层对磁热冲击下圆筒位移和应力的影响,将3.2节中双层圆筒的内层和外层分别替换氧化铝-铝合金FGM,材料性质呈指数函数分布,表达式为: P= (17) 其中:Pc、Pm分别为氧化铝和铝合金的材料性质;η为FGM的梯度分布因子;rin≤r≤rout,rin、rout分别为功能梯度层的内半径和外半径。圆筒内层替换为功能梯度层时,rin=a,rout=(a+b)/2;圆筒外层替换为功能梯度层时,rin=(a+b)/2,rout=b。 图8 内、外层分别替换为功能梯度层时r*=0.525处随t*的变化 图9 内、外层分别替换为功能梯度层时r*=0.525处随t*的变化 图10 不同η下r*=0.525处随t*的变化 图11 不同η下r*=0.525处随t*的变化 本文在空间域应用状态空间法,在时域应用Newmark法,研究轴对称非均质无限长圆筒受磁热冲击时的动态响应,通过算例证实本文解的正确性和有效性,探讨双层均质材料组合圆筒、将其内层或外层换为功能梯度层时对缓解磁热冲击下圆筒动态响应的影响,分析功能梯度层梯度分布因子对磁热冲击下动应力峰值的影响,得到如下结论: (1) 得到的半解析解可用于任意梯度空心圆筒受磁热冲击作用时的动态响应分析。 (2) 适当地延迟热冲击时间,可以显著降低磁热冲击下双层均质材料组合圆筒的动应力振幅。 (3) 将双层圆筒内层材料更换为FGM,选取合适的功能梯度分布因子,可有效降低磁热冲击下的圆筒内动应力的峰值。3 数值算例与结果讨论
3.1 均质圆筒




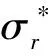

3.2 双层均质材料组合圆筒


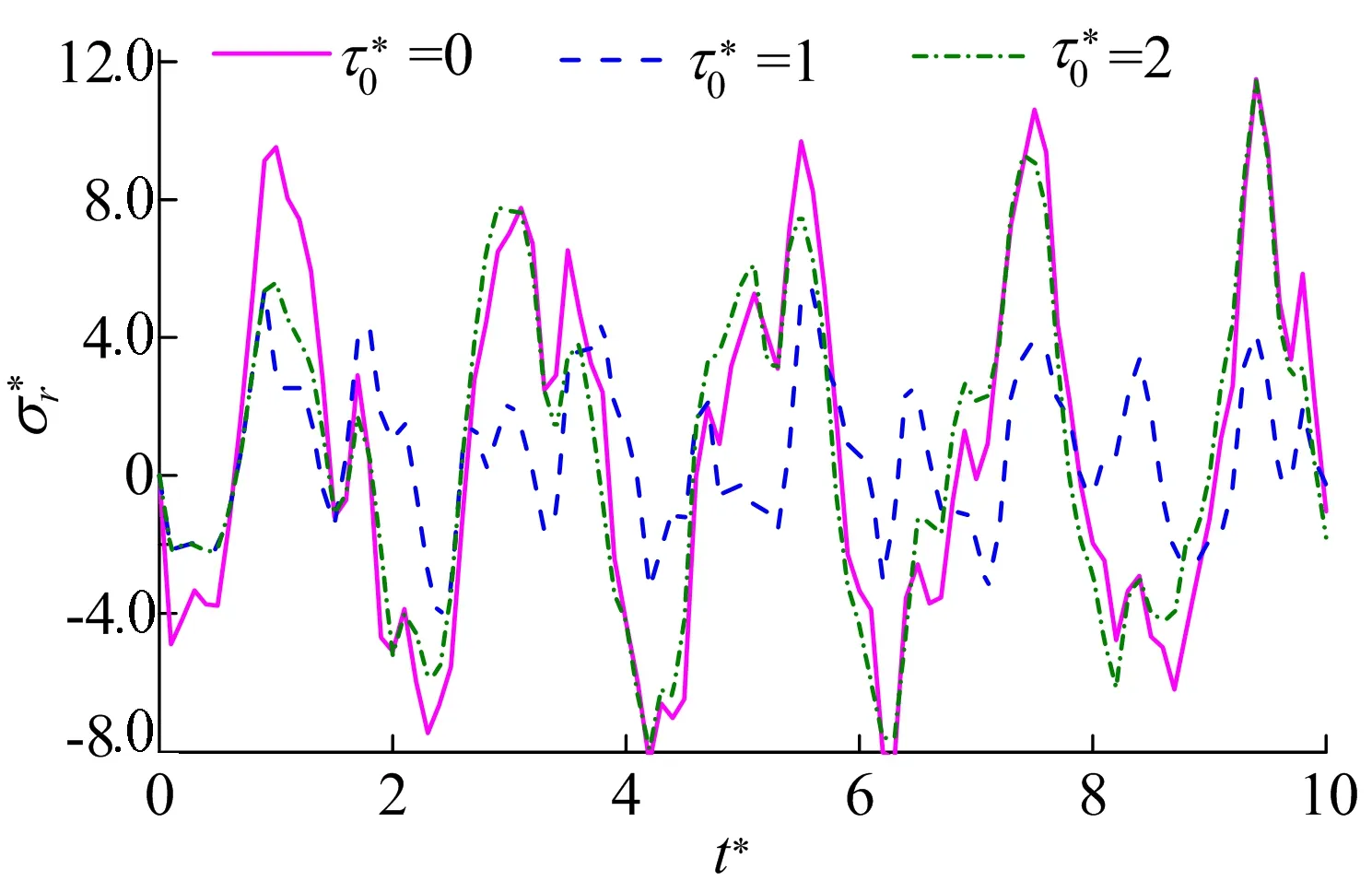
3.3 含FGM的双层圆筒

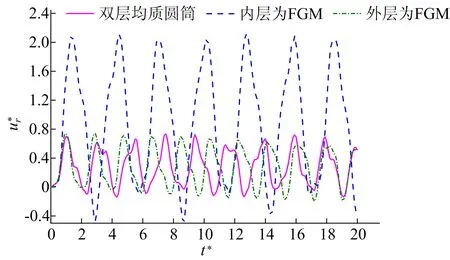


4 结 论
