双重下采样增强的点云改进配准算法研究 *

陈仲生，李潮林，左 旺，侯幸林

（1.常州工学院汽车工程学院，常州 213032；2.湖南工业大学电气与信息工程学院，株洲 417002）

前言

目前自动驾驶的4 大关键技术包括感知技术、决策技术、路径规划和运动控制，其中环境感知是智能车辆自主行驶的基础和前提。特别是在自动驾驶环境感知系统中，如何获取高精度实时路况数据是决定自动驾驶系统行车安全的关键。近年来，激光雷达、毫米波雷达等先进传感器技术正成为汽车自动驾驶领域的重要感知手段，其输出的点云已成为描述车辆所处三维世界的主要数据格式［1］。但是实际应用中，受传感器视场角限制，单个传感器往往只能获得有限视野范围内的点云，需要采用配准算法才能生成完整场景的三维点云，以便支持后续的物体识别、分类及路径规划。点云配准就是估计两帧扫描点云之间的变换矩阵，将不同条件下采集的点云数据变换到同一坐标系下，实现点云数据的拼接或融合以获得完整的3D 数字模型，它是自动驾驶点云数据处理不可缺少的重要前序步骤［2］。

点云配准也是计算机视觉领域的研究热点之一。Huang 等［3］对点云配准研究进展进行了综述与展望，根据采集设备类型分为同源点云配准和跨源点云配准，根据发展阶段分为传统的配准方法和基于学习的配准方法。传统点云配准方法主要基于优化思想，包含粗配准和精配准两个阶段：点云粗配准目的是对任意初始位置的两个点云进行粗略的配准使其大致对齐，为后续精配准提供良好的初始位置，主要包括基于全局搜索思想的配准和基于几何特征描述的配准两大类算法；精配准是在粗配准的基础上，进行更精确、更细化的配准。基于学习的配准方法是从点云数据中学习出三维特征实现配准，其不足是需要大量训练数据，对于未知场景配准性能较差［3］，这在自动驾驶这种实时性要求高、未知场景多的应用场合中存在较大的局限性。

应用最广的点云精配准算法是Besl 和Mckay［4］提出的迭代最近点（iterative closest point，ICP）算法，但它对点云初始位置要求较高，需要两个点云的重叠度高且数据量相近，否则容易陷入局部最优解，而且存在迭代速度慢、配准时间长等不足；Magnusson等［5］提出了另一种经典的正态分布变换（normal distributions transform，NDT）配准算法，NDT 算法的配准效果与ICP 算法相似，其改进实质等同于将ICP算法栅格化。可以看出，ICP、NDT 算法及其变体大多需要点云初始位置大致对齐，这种简单的点与点对应导致鲁棒性较差，为此人们开始研究更加鲁棒的对应，比如点对面、面对面和特征对特征，常见的点云特征描述有快速点特征直方图（fast point feature histograms，FPFH）描述子、内部形状描述子（intrinsic shape signature，ISS）［6］、三维Harris 描述子（harris 3D，H3D）［7］等，其中ISS是一种表示立体几何形状的算法，具有丰富的几何信息，用于关键点提取时具有快速、高效、稳定等优点。同时，人们研究了不同的粗配准算法，比如Aiger 等［8］提出的全等四点集（4-points congruent sets，4PCS）经典粗配准算法，不需要提供初始位姿就能为精配准提供良好的初始位姿，缺点是计算速度慢；为此Mellado 等［9］提出了一种Super4PCS 算法，它在提取四点集的同时去除错误的点集，降低了一定的时间复杂度。Super4PCS算法的特点是不需要初始位姿，但计算速度仍然不快，可以作为粗配准算法为ICP 等精配准算法提供良好的初始位姿。为了提高点云配准的速度和正确率，近年来人们提出了不同的点云配准增强方法。李仁忠等［10］将ISS 与ICP 算法结合，提高了ICP 算法的配准精度，但仍然依赖初始位姿；宗晓萍和吴岩［11］提出一种基于FPFH 特征的ICP 改进算法，可以提高配准的精确度；单丽杰等［12］利用法向量夹角提取特征点，提高ICP 算法的配准速度；王月海等［13］采用自适应体素网格滤波法对点云进行处理，一定程度上提升了配准效率；范强等［14］将H3D 与NDT 相结合，提升了配准精度，但鲁棒性不高。综合来看，已有改进ICP 配准算法虽然在一定程度上提高了配准精度和速度，但目前大多数4PCS 和ICP 变体算法仍无法满足自动驾驶等实时性要求高的应用场合［15］。

进一步分析可知，限制4PCS 和ICP 及其变体算法配准速度的主要原因在于寻找几何形状相似的点集以及验证其变换矩阵均比较费时。为此，本文引入点云双重下采样来快速减少点云数目，并融合ISS、Super4PCS 和ICP 算法的优点，研究一种改进的快速点云配准方法，其特点是采用双重下采样快速降低点云数据，同时利用ISS 算法来优化Super4PCS算法，降低时间复杂度，同时提供良好的初始位姿，以提高整个算法的配准速度和精度，最后利用斯坦福点云数据集和自动驾驶点云数据集进行验证。

1 改进配准算法的基本框架

针对已有点云配准算法存在速度低的问题，本文提出的改进型双重下采样增强的点云快速配准算法基本框架如图1 所示，主要包括以下3 个步骤：点云数据双重下采样、ISS-Super4PCS粗配准和线性最小二乘优化ICP 精配准。在双重下采样阶段，首先使用体素下采样对原始点云数据进行粗采样，快速减少点云数目，然后使用基于法向量的邻域夹角进行精采样，充分保留点云数据的原始特征；在粗配准阶段，首先提取双重下采样后两个点云的ISS 特征点，减少Super4PCS 算法的一致性4 点搜索范围，然后基于ISS 特征点利用Super4PCS 算法求出粗配准变换矩阵；在精配准阶段，利用线性最小二乘优化ICP 配准算法对粗配准的结果进一步优化，实现精配准。

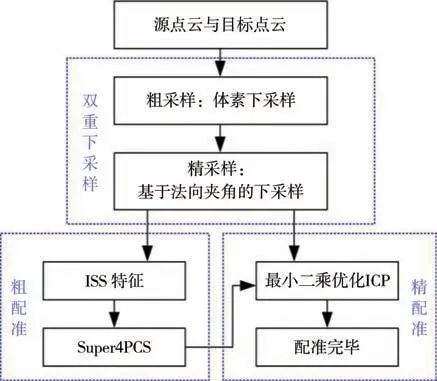
图1 改进型配准算法基本框架

上述点云配准改进算法的优点在于：通过双重下采样操作可以快速减少点云的数据量，从而大大降低后续配准过程的时间复杂度；同时，保留了Super4PCS算法的鲁棒性。因此，该算法同时具有鲁棒性好、配准精度高、配准速度更快的优点。

2 点云数据双重下采样

实际应用中点云的数据量往往很大，直接进行处理不仅计算量大，而且配准效率低。为此本文提出对点云数据进行双重下采样，包括粗采样和精采样，以降低后续点云配准的时间复杂度。

2.1 基于体素下采样的粗采样

已有研究表明，体素格滤波器在进行向下采样的同时不会破坏点云的数据结构［16］，故采用体素下采样方法进行粗采样。体素下采样是根据输入点云数据创建一个三维的体素栅格，每个体素栅格用栅格内全部点的质心来表示，其计算表达式为

式中：Xi、Yi、Zi分别是第i点的3 个坐标；m是体素栅格内点的数量。

2.2 基于邻域点云法向夹角下采样的精采样

体素下采样虽然不破坏点云的数据结构，但是如果体素栅格过大就会损失点云的特征。为此，采用基于邻域点云法向夹角的下采样方法对粗采样点进行精采样，进一步减少点云数量，且保留点云原始特征。

基于法向夹角的下采样是计算一个点在一个邻域内与其他所有点法向夹角的平均值，如果该均值大于设置的阈值，则认为该点是特征点，需要保留，计算公式为

式中：θ是平均夹角；m是邻域内所有点的数量；α是选取点的法向量；β是邻域内其他点的法向量。需要指出的是，这里阈值的选取是精采样中的重要环节，需要考虑两个因素：一是后续配准速度要求精采样后的点数不能太多，故阈值不能过大；二是后续配准精度要求精采样后的点数不能太多，故阈值不能过小。但目前如何具体设置阈值仍缺乏统一标准，往往需要针对实际点云数据大小及其配准性能要求采用尝试方式来确定。

3 改进配准算法设计

3.1 ISS-Super4PCS粗配准

由于Super4PCS 算法对初始位姿具有很好的鲁棒性，故选用它进行粗配准。但为了保留点云的原始特征信息，双重下采样后的点云数据不可能降到最低，直接进行配准计算量仍然较大。针对此问题，常用的解决方法是提取特征点集后再进行配准，可以大幅减少点云数量、降低时间复杂度。特别是在常见的几种特征描述子中，ISS 具有丰富的几何信息，有利于提高点云配准精度。为此本文提出将ISS和Super4PCS 结合起来进行粗配准，其改进之处在于引入ISS 算法将下采样后的初始点云缩减到ISS特征点集，使得Super4PCS 粗配准在特征点集上进行，可以大大缩短四点对提取和匹配时间。

3.1.1 ISS特征点提取

针对双重下采样后的点云数据，ISS特征点提取的主要步骤如下。

（1）对每一个点Pi设定一个搜索半径r。

（2）计算查询点Pi与邻域内各点的欧氏距离，并设定权值Wij，权值表达式为

（3）计算每个查询点Pi与邻域内所有点的协方差矩阵cov(Pi)：

3.1.2 Super4PCS粗配准

与已有方法不同，这里Super4PCS 粗配准是在ISS特征点集上进行的。记点云P、Q分别为源ISS特征点集和目标ISS 特征点集，则Super4PCS 粗配准主要步骤如下。

（1）在源ISS 特征点集中选取4 个共面不共线的4 个点a、b、c、d作为点基（必须是P、Q重叠区域中的点），且ab和cd相交于点e，夹角为θ，利用式（6）计算两个比率和两个点距。

对于Q中每个点qi，以它为球心分别以λ1、λ2半径做球面，设置阈值ε、qi与球面[λ1-ε，λ1+ε]范围内的点满足S1，qi与球面[λ2-ε，λ2+ε]范围内的点满足S2。

（3）针对S1和S2中的每个对点，连线并存储对应的方向向量角，再基于仿射不变性原理分别计算由比率r1、r2确定的交点e1、e2。

（4）在S1和S2中搜索与e1、e2近似对等的点，且两点对连线的夹角近似等于θ，则在目标ISS 特征点集中找到点基对应的四点集。

（5）根据对应点集和点基计算变换矩阵T，利用T对源ISS 特征点进行变换，统计变换后的点云与目标ISS 特征点集中最近点距离小于某个阈值δ的点的数目，该数目表征T的质量。迭代进行上述4个步骤，直至找到最优的T使得两个ISS特征点集足够接近，此时T即是粗配准的结果。

3.2 线性最小二乘优化ICP精配准

经过ISS-Super4PCS粗配准后，源点云和目标点云具有良好的初始位姿，再采用点到面ICP 算法进行精配准，可以减少对点云初始位姿的依赖，提高配准精度。具体来说，就是将双重下采样后的点云（以下称D-源点云和D-目标点云）和粗配准变换矩阵T输入到ICP 配准算法中，用于源点云与目标点云的精配准。

经典的点到面ICP 配准算法中常使用非线性最小二乘法来求解，但当两个点云之间相对旋转角度小于30°时，可以采用线性最小二乘优化逼近非线性最小二乘优化。本文中经过上述粗配准后，D-源点云与D-目标点云之间的位置已经非常接近，相对旋转角度可近似为0，为此本文采用了线性最小二乘优化求解方法，它不但可以加快ICP 配准速度，而且可以进一步提高配准精度。具体步骤如下。

（1）利用粗配准变换矩阵T对D-源点云进行变换，得到精配准的初始D-源点云。

（2）对D-源点云中的任意点pi，在D-目标点云中搜索与pi相应的最近点qi，pi与qi构成对应点对，从而形成对应点对集。

（3）以对应点对平均距离最小为目标函数，采用线性最小二乘优化计算得到D-源点云与D-目标点云之间的旋转矩阵R和平移矩阵Γ，由R和Γ可以得到刚体变换矩阵M。

（4）利用刚体变换矩阵M对初始D-源点云进行变换，得到新的D-源点云，再重复步骤（2）。

（5）设定阈值ε与迭代次数k，当对应点相对平均距离小于阈值或总迭代次数大于k时，则迭代结束；否则依次执行步骤（2）～步骤（5），直至获得最优的刚体变换矩阵M，从而完成精配准。

4 基于标准点云数据集的算法验证

为了验证本文提出的点云改进配准算法，分别选取公开的斯坦福点云数据集和自动驾驶场景Kitti数据集作为目标点云。硬件环境为Intel（R）Core（TM）i5-10400F CPU@ 2.90GHz 处理器/8GB 内存/64位win10操作系统，软件环境为Visual Studio2019/开源点云库PCL1.11.1/C++语言。

4.1 基于斯坦福点云数据的配准算法验证

采用的斯坦福点云数据包括兔子（bunny）点云模型、龙（dragon）点云模型和犰狳（armadillo）点云模型，再人工对上述点云模型进行变换作为源点云。兔子点云模型1 为沿X轴平移0.4 m、绕Y轴旋转45°；兔子点云模型2 为沿X轴反方向平移0.2 m，绕Y轴旋转30°；龙点云模型1 为沿Y轴平移0.4 m、绕X轴旋转45°；龙点云模型2 为沿X轴反方向平移0.2 m，绕Y轴旋转30°；犰狳点云模型1 为沿X轴平移0.4 m、绕Y轴旋转45°；犰狳点云模型2 为沿X轴反方向平移0.2 m，绕Y轴旋转30°。

为了评价点云配准算法的性能，这里选取对应点相对距离的均方根（RMSE）作为配准误差度量指标，RMSE越小，表明配准精度越高；同时计算配准过程所用的时间，用于度量配准的速度。3 种斯坦福点云模型的最终配准结果如表1 所示（红色是目标点云、绿色是源点云），且粗配准和精配准结果分别如表2 和表3 所示，其中精采样的阈值设为10°。从表1～表3可以看出：对于不同初始位姿的源点云，均获得了较好的配准结果，验证了本文算法的鲁棒性；针对不同的点云模型，均获得了很好的配准结果，从而验证了本文算法的配准精度。

表1 3类斯坦福点云模型

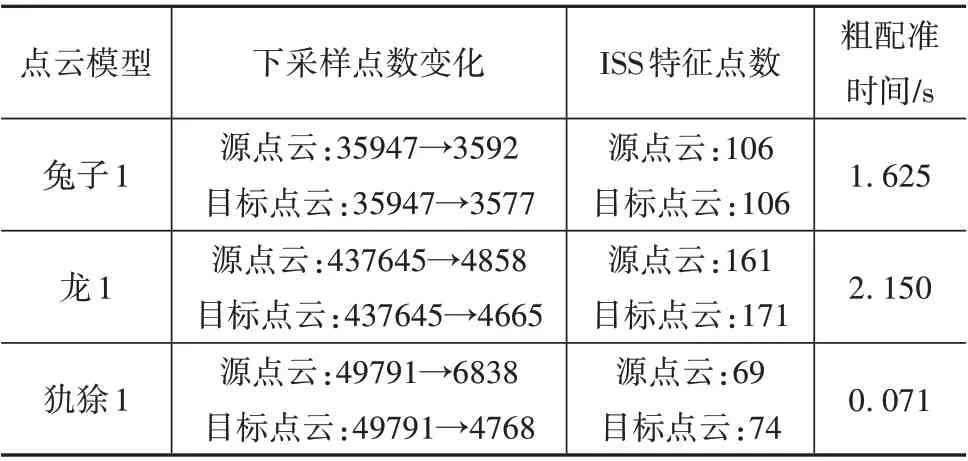
表2 3类斯坦福点云模型粗配准结果

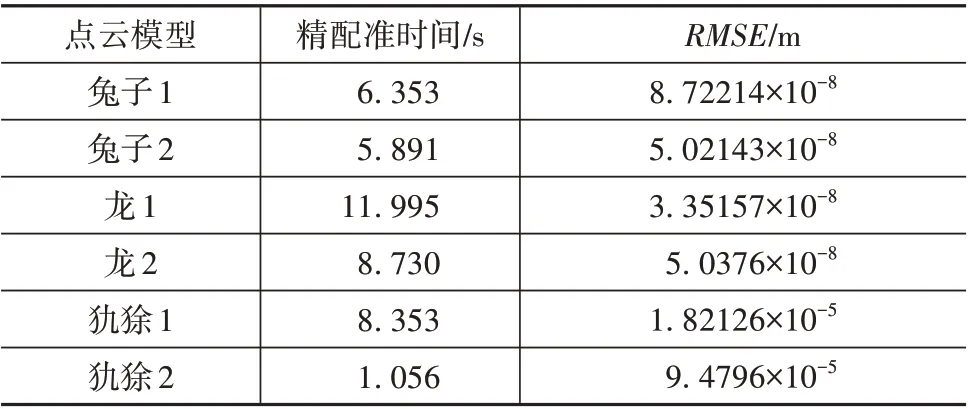
表3 3类斯坦福点云模型精配准结果

为了进一步验证本文算法的优越性，这里将本文算法与已有文献中的改进点云配准算法进行对比。验证数据集为斯坦福兔子点云模型，对比的算法既包括与本文算法相近的ISS+ICP 算法和Super4PCS+ICP 算法，又包括其他文献里的NDTICP 算法［17］和SAC-IA+ICP 算法［18］，对比验证计算结果如表4所示。

由表4 可以看出：本文算法的配准精度明显高于ISS+ICP 和Super4PCS+ICP，分别提高了约2 个和3 个数量级，配准速度分别约为ISS+ICP、Super4 PCS+ICP 的47.66%和41.96%，配准速度显然更快；本文算法的配准精度也明显高于NDT+ICP 和SAC-IA+ICP，分别提高了2 个和1 个数量级，配准速度分别 约 为NDT+ICP 和SAC-IA+ICP 的33.33% 和11.11%，配准速度也更快。上述对比结果充分验证了本文算法的优越性。

表4 与已有配准算法对比结果

4.2 基于自动驾驶Kitti数据集的配准算法验证

Kitti数据集由德国卡尔斯鲁厄理工学院和丰田美国技术研究院联合制作的，也是目前国际上自动驾驶场景下常用的评测数据集［19］。Kitti数据集的采集平台装配有2台灰度摄像机、2台彩色摄像机、1台Velodyne 64 线3D 激光雷达、4 个光学镜头以及1 个GPS导航系统。这里选用Kitti数据集的街道点云数据集作为目标点云，再将其沿X轴正方向移动5 m、绕Y轴转动30°变换作为源点云，如图2所示（其中绿色为源点云，红色是目标点云），然后利用本文提出的算法进行配准（其中精采样的阈值设为15°），结果如表5 所示，可以看出在街道点云数据集上同样验证了该算法的配准速度快。

图2 街道源点云和目标点云数据集

表5 自动驾驶街道点云模型配准结果

5 结论

针对当前ICP 及其变体配准算法存在的对初始位姿要求较高、配准速度慢等问题，本文提出了一种双重下采样方法对初始点云数据进行预处理，在保留点云原始特征的同时大大减少了点云数据量；然后集成ISS、Super4PCS 和ICP 算法的优点，研究了ISS-Super4PCS粗配准方法和线性最小二乘优化ICP精配准算法，并利用斯坦福点云数据集和自动驾驶Kitti 点云数据集进行了实验测试和对比验证，结果表明本文算法具有更高的配准精度和更快的配准速度，更适用于自动驾驶领域的点云配准。今后，将进一步对本文算法中的阈值设定问题进行研究，降低阈值对算法配准性能的影响。