基于水动力学模拟的灌区输配水系统优化调控模式研究

吴彩丽，白美健，张宝忠，史 源，侯文涛，赵 智

（1.国家节水灌溉工程技术研究中心（北京），北京 100048；2.中国水利水电科学研究院 水利研究所，北京 100048；3.水利部数字孪生流域重点实验室，北京 100038）

0 引 言

灌溉系统在渠首工程以下主要包括输配水工程和田间工程两个部分。输配水工程承担着把灌溉用水从水源“及时、足量、稳定”的输送至田头的作用，是实施农业灌溉极其重要的一个环节；田间工程是将灌溉用水从田头继续输送到田间作物，确保农作物的根系活动层土壤的湿润，满足农作物的吸收和农作物生长需要。近年来，新疆建设兵团田间高效节水灌溉技术发展一直走在我国的前列。据2021年兵团统计年鉴数据，截止2020年底，兵团总灌溉面积163.96 万hm2，节水灌溉面积136.79 万hm2，其中滴灌面积131.54 万hm2，滴灌面积占总灌溉面积的80%，是我国规模化滴灌面积比例最高的地区。据上述数据及调研所知，新疆建设兵团的渠道衬砌、田间高效节水技术等已经大面积推广，基础设施建设已相对成熟。目前，兵团农业节水最突出的问题是先进的田间滴灌工程对应着低水平、粗放型的渠道输配水系统运行管理，兵团灌区普遍存在着输配水过程和滴灌作物需水过程不匹配、作物关键生育期需水得不到满足、信息化管理程度不高等问题，使得先进的田间滴灌技术难以发挥应有效益。因此，兵团灌区亟需研究与滴灌作物灌溉制度相匹配的渠道输配水调控技术，在灌溉中需要根据棉花、红枣、玉米等典型农作物所需的滴灌灌溉制度，结合实际情况制定适合作物需水过程的输配水方案，指导作物科学合理灌溉。

灌溉渠系调控是运行管理灌溉渠系输配水系统的能力，通过控制渠道沿程的水工建筑物，按照设计要求和调度计划，在保证渠系运行安全的前提下，将灌溉水适时适量地输送至用水单元。近年来，国内外对渠系水资源优化配置方面进行了大量研究。Mohammad等（2005年）以灌溉需水量和配水量差异最小为控制目标，建立渠道优化配水模型，并采用模拟退火技术进行求解，并进行实例验证，结果表明得到优化配水方案合理可行。吴彩丽等（2007年）以供水量最大、缺水量最小等指标为目标函数，建立了基于流量分配的渠系多目标动态规划配水模型，可探求不同权重目标函数条件下，渠系流量的实时分配情况，采用人工神经网络方法进行求解，并在某大型灌区进行了实例验证，结果合理可行；徐淑琴等（2020年）针对黑龙江杨木灌区的灌排两用渠道，以渠道输水过程中水量损失最小、不同时刻干渠净配水流量变化最小、灌排净效益最大为目标函数，建立输水优化调度模型，采用多目标遗传算法NSGA—II优化，求解上级渠道最优灌溉水位以及下级渠道不同流量输水方案，优化结果提高了灌溉水利用效率，增加了灌排净效益；肖梦君等（2022年）采用实时灌溉预报模型计算作物实时需水，根据灌区渠系运行情况建立多目标渠系配水模型，并采用模拟退火算法求解。选择黄河流域的二级渠系进行实例研究，与原灌区配水计划相比，配水时间减少了1.2 d，总配水量减少了8.3%，渠系损失水量减少了6.84%。

综上，可以看出，对于灌区渠系输配水调控技术的研究多围绕渠系优化配水模型构建和模型求解算法，按照毛灌溉用水量、灌溉面积或灌溉预报模型确定各区域的灌溉用水量，以配水时间减少、配水流量集中、输水损失小、灌溉效益提高等为目标函数，采用最优化方法，计算某段时间内渠系配水流量的最优时空分配（配水时间和配水流量），以便在灌溉开始前制定合理的配水计划。科学合理的渠系配水计划能够减少水量损失，提高灌溉效率，但是，由于目前的研究大多对渠道水动力学过程考虑不足，此类模型很难预测配水计划在实施过程中可能发生的渠道漫溢、供水能力不足、供需分离等问题，且闸门开闭的具体时间多依赖于调度员的经验。现有渠道输配水调控方面的研究多针对地面灌溉，较少针对滴灌的研究，而地面灌溉与滴灌有很大的不同，滴灌具有高可控性和精准性，在灌溉制度上具有高频性、灌溉周期短的特点，更需要严格按照作物的生长期按时按量进行灌溉。

因此，本研究从水动力学模拟入手，针对兵团灌区某一次灌溉过程中输配水和作物需水不匹配问题，根据当前时段的供水和需水情况，借助水动力学模型精确模拟渠道输配水过程，建立优化调度模型，并采用最优化方法求解，寻求满足本次灌溉需水和渠系调度运行约束的最优调度方案，以便在渠道运行安全的前提下，把灌溉用水快速、足量的输送至田间。在此基础上，本研究提出了灌区输配水优化调控模式，实际灌溉中可根据灌溉需水情况采取相应的调控模式，指导灌区每一次灌溉过程。

1 研究区概况

本研究选择兵团某中型灌区进行研究。该灌区位于天山北麓，准葛尔盆地，古尔班通古特大沙漠南缘，地理位置东经85°52'～86°12'，北纬44°31'～44°46'。项目区地处温带，远离海洋，具有大陆性干旱气候特征，冬季长而寒冷，夏季短而炎热，昼夜温差大，光照充足，热量丰富，降雨稀少，蒸发量大，自南向北年温差逐渐增大，降水量逐渐减少，蒸发量逐渐增加。多年平均气温8.1 ℃，1月份月平均气温-16.5 ℃，7月份平均气温25.6 ℃，日照2 732 h，无霜期155 d，最大冻土深1.64 m。年平均降水量117.2 mm，降水主要集中在4-8月，占全年降水量的70%左右，年平均蒸发量1 943.8 mm。

灌溉水源为水库，总灌溉面积13 740 hm2，灌区骨干渠系由总干渠、一分干、二分干、一至五支渠组成，干渠总长度31.6 km，支渠总长度7.3 km，灌区骨干渠系布置见图1，干支渠相关参数见表1。灌区主要作物为小麦、红枣、棉花，田间灌溉方式均为滴灌，滴灌灌溉制度为：小麦、红枣、棉花每年的滴灌灌溉定额分别为4 050、4 620、4 200 m3∕hm2，其中，小麦每次的灌水时间及灌水定额分别为4月（上旬450 m3∕hm2、中旬450 m3∕hm2、下旬525 m3∕hm2）、5月（上旬525 m3∕hm2、中旬450 m3∕hm2、下旬450 m3∕hm2）和6月（上旬450 m3∕hm2、中旬375 m3∕hm2、下旬375 m3∕hm2）；红枣每次的灌水时间及灌水定额分别为4月（下旬900 m3∕hm2）、5月（中旬750 m3∕hm2）、6月（上旬600 m3∕hm2、下旬300 m3∕hm2）、7月（上旬450 m3∕hm2）、8月（上旬225 m3∕hm2、中旬600 m3∕hm2）、9月（上旬645 m3∕hm2）；棉花每次的灌水时间及灌水定额分别为4月（上旬255 m3∕hm2、中旬255 m3∕hm2）、6月（上旬300 m3∕hm2、中旬390 m3∕hm2、下旬390 m3∕hm2）、7月（上旬390 m3∕hm2、中旬420 m3∕hm2、下旬420 m3∕hm2）、8月（上旬390 m3∕hm2、中旬330 m3∕hm2、下旬390 m3∕hm2）和9月（上旬315 m3∕hm2）。

图1 典型灌区骨干输配水渠道系统图Fig.1 Typical irrigation backbone water distribution channel system diagram

表1 干支渠道相关参数表Tab.1 Table of relevant parameters of trunk and branch channels

2 模型及求解

2.1 模型构建

为寻求渠系运行的最优调度方案，本文根据滴灌作物的灌溉制度计算当前时段的需水情况，以干支渠灌溉耗时最短为第一个目标函数（灌溉耗时最短，缩短灌溉周期，保证水流快速通过渠道进去田间滴灌系统）；以干支渠在配水时段内弃水最少为第二个目标函数，建立渠系输配水优化调控模型。基于一维圣维南方程描述渠道输配水系统的水流运动过程，输入干渠入口的配水流量，模拟整个干支渠的水位和流量变化过程，经反复试算，得出本次渠系调度运行的最优调度方案。

2.1.1 目标函数

式中：i为渠道编号；j为配水时段编号；Δti为配水时段内通过渠道i的时间，d；Wi为通过的水量，m3；qi为配水流量，m3∕s；T为总配水时间，d；W弃ij为第i条渠道第j个时段的弃水，m3，渠道弃水量为渠道输水量与灌溉需水量的差值。因兵团灌区的骨干渠系基本上都进行了衬砌，本研究模型中不考虑渠道输水渗漏损失，也即本模型适用于衬砌渠道。

2.1.2 约束条件

（1）水量约束：采用不同作物滴灌的灌溉制度计算不同灌溉时段需要的灌水量，一个灌溉周期内作物需水量不大于渠道系统输配水量。

（2）流量约束：渠道输水过程中，各渠道水流流速需在不冲不淤流速之间，v不淤＜qi∕Ai＜v不冲；Ai为第i条渠道过流断面面积，m2。

本研究采用一维圣维南方程描述渠道输配水系统的水流运动过程：

①控制方程。基于断面流速平均假设，圣维南方程组(Saint-Venant Equations)能够合理的描述渠道水流运动过程，在实际工程中的应用也非常广泛，本文取水位ζ和流量Q为因变量的向量形式的一维圣维南方程组描述明渠水流运动过程，控制方程如下：

式中：U为因变量向量；F为对流通量项；t为时间坐标；x为空间坐标；Sζ为水力坡度项；Sf为摩阻项；Sin为入渗项；SP为分水项。

式（4）的向量形式表达式如下：

式中：A为渠段的过流断面面积，m2；ζ为水位，m；h为地表水深，m；B为渠段的自由水面宽度，m；Q为通过渠道的流量，m3∕s；Ω为分水口的自由水面面积，m2；u为过水断面流速，m3∕s；g为重力加速度，9.8 m∕s2；R为水力半径，m；I为地表水入渗系数；n为曼宁糙率系数；Qi为从渠段i的分水汊点流出∕入的流量，m3∕s；φi为符号函数，若Qi为流入态，φi=1，否则φi=-1。

②初始与边界条件。渠道的初始条件为水位ζ=HI+zb。其中，HI为最小水深假设，是为了避免在计算过程中出现除数为零导致计算出错的情况。上游边界条件为灌区水源的引水流量；引水停止后，相关节点流量设置为零。下游边界在非排水期设置为封闭状态，即Q=0，排水期设置为自由出流条件，即根据渠道内水深插值获得渠尾水位，强排处设置为相应的强排流量。

2.2 求解方法

本研究采用遗传算法求解优化调控模型，采用有限体积法求解圣维南方程，调控优化方法的逻辑框图如图2所示。

图2 调控优化方法的逻辑框图Fig.2 Logic block diagram of the regulation optimization method

2.2.1 遗传算法

本研究采用遗传算法求解优化调控模型，以渠道配水的时间t和流量q为决策变量，用长度为10位的二进制编码串来分别表示2个决策变量t，q。计算过程如下：

（1）根据实际情况假定t，q的取值范围。以渠道i为例，配水时间为ti，过水流量为qi，过水流量的取值范围需要利用渠道的不冲不淤流速和渠道断面进行计算，配水时间的取值范围为一个灌溉周期内控制面积上作物的需水量除以过水流量。

（2）确定编码方法与解码方法。10位二进制编码串可以表示从0到1 023之间的1 024个不同的数，故将ti，qi的定义域离散化为1 023个均等的区域，包括两个端点在内共有1 024个不同的离散点。ti，qi的二进制编码分别记为ti(2)，qi(2)。解码时需先将20位长的二进制编码串切断为2个10位长的二进制编码串，然后分别让它们转换为对应的十进制整数代码，ti(2)对应的十进制数记为ti(10)，qi(2)对应的十进制数记为qi(10)。

（3）确定个体评价方法。渠系输配水优化调控模型的目标函数是求函数的最小值问题，为满足适应度函数取非负值的要求，将目标函数值y变换为个体适应度Y的公式如下：

式中：Cmax为适当地相对比较大的数。

（4）设计遗传算子以及确定运行参数。选择运算使用比例选择算子，交叉运算使用单点交叉算子，变异运算使用基本位变异算子，实际应用中，应根据具体实例确定需采用的群体大小、终止代数、交叉概率、变异概率。

2.2.2 数值解法

本文采用结合矢通量分裂格式和双时间步法的有限体积法，该方法具有无条件稳定特性，且易于隐式求解，采用该方法求解双曲型的圣维南方程组，能够实现高精度和高效率的统一。空间离散过程中，方程的积分形式如下：

式中：i为单元格编号。

以连续性方程中的水位变量为例，任意单元格边界（i+上对其进行二阶重构，为了防止数值振荡，采用min mod限制器计算Δζi和Δζi+1。

基于高斯散度定理，对流项的空间离散形式如下，

利用前面构建的各个对流分量的黎曼形式，确定对流项的计算方法，其中需要注意的是，采用AUSM格式计算流速分量中的弗劳德数：

式中：λi+1∕2,L和λi-1∕2,L为单元格边界（i+1∕2）处的弗劳德数的分裂函数，限于篇幅，具体形式见文献[18]。

最终得到的离散格式如下：

式中：αi，βi，γi，ηi为方程经过空间重构和AUSM格式离散后得到的系数。

此外，源汇项中，Sζ采用中心差分方法计算，Sf=-fiUi，Sin=-IiUi，Sp直接利用单元格的中心值计算。

本团队针对上述方法研发了数值模拟与优化调控相关软件。

3 分析与讨论

3.1 建立模型

基于第1节典型研究区的设计资料图，采用本团队研发的水动力学模拟与优化调控软件，首先构建兵团某中型灌区骨干渠系的拓扑模型。骨干渠系拓扑模型见图3，该拓扑模型主要分为田块层、管渠土层和区域边界层；其次，对骨干渠系进行网格剖分。本实例剖分为10 000个网格，其中，骨干渠系及典型剖分节点示意图见图4，骨干渠系的引水闸、分水闸位置即为典型节点，干渠、一分干、二分干、一至五支渠的典型节点编号分别为61、7973、133、9005，3015、6184、345、4477。骨干渠系总体的网格剖分见图5；然后，对剖分好的骨干渠系拓扑模型进行数值模拟与优化调控计算。

图3 典型灌区渠系建模图Fig.3 Modeling diagram of canal system in typical irrigation area

图4 骨干渠系及典型剖分节点示意图Fig.4 Schematic diagram of trunk canal system and typical dividing nodes

图5 骨干渠系总体网格剖分图Fig.5 Partition grid diagram

3.2 优化调控结果与分析

通过3.1节利用软件构建模型，进行数值模拟与优化调控计算，本节对计算结果进行分析与探讨。以6月上旬的灌溉为例，灌区所有作物小麦、红枣、棉花都需要进行滴灌灌溉。小麦、红枣、棉花6月上旬的灌水定额分别为450、600和300 m3∕hm2。灌区干支渠是续灌，支渠以下为轮灌。当所有轮灌组灌溉结束后（一般为渠道最末端的轮灌组），支渠分水口闸门关闭。模型输入参数：干渠口入流量(m3∕s)、各干支渠断面尺寸(m)、长度(km)、渠道节点高程、不冲不淤流速、节点闸门开度、种植作物面积及灌水定额等。输出参数：干支渠各典型节点随时间变化的流量(m3∕s)、水位(m)，以及优化控制方案。以干渠口闸门开启，渠首开始取水为本次灌溉的计时起点。

根据数值模拟结果，骨干渠系各个关键节点的模拟流量、水位变化曲线见图6和图7。

图6 各关键网格节点模拟流量变化过程图Fig.6 Simulated flow variation process diagram of each key grid nod

图7 各关键网格节点模拟水位变化过程图Fig.7 Simulated water level change process diagram of each key grid node

图6是骨干渠系各个关键节点的流量随时间的变化过程线，图7是骨干渠系各个关键节点的水位随时间的变化过程线。从图6和图7可以看出，总干渠、一分干、二分干、五支渠陆续开始输水，三支渠、四支渠紧随其后开始输水，一支渠和二支渠由于距离渠首较远，在四天多的时候才开始输水。骨干渠系各个关键节点关闭闸门的时间也长短不一，输水时间的长短跟各干支渠控制灌溉面积及渠道本身的过水流量等因素有关，田间控制面积大的渠道所需通过的灌水量大，而如果渠道本身过水流量大的话，能够使水流迅速通过，节省输配水时间，否则，该渠道就需要较长的输配水时间。

此外，当闸门突然关闭时，受上游壅水的影响，此时渠道水位和流量均出现不同程度的增大，从图6和图7中可以看出，闸门关闭时渠道过水流量和水位曲线均有轻微上扬，这也说明了本研究提出的水动力学模型模拟结果是精确的，能够反映出渠道水面细微的变化。

经反复试算，得出本次渠系调度运行的最优调度方案见表2。

表2中，关键网格节点即渠道引水闸或分水闸所在位置，一分干控制一支渠、二支渠和斗口直接灌溉的面积，二分干控制三支渠和四支渠。各骨干渠道控制面积上种植的作物及面积不同，各作物的灌水定额也不同，从表2中优化得出的控制方案可以看出，针对6月上旬的灌溉，以总干渠引水闸为例，从0分钟开始开启，到17 168分钟关闭；一分干闸门从第21分钟开启，到17 168分钟，和总干渠闸门一同关闭；其余各分干及支渠的闸门开闭时间均根据优化所得，各不相同。各分干及支渠距离总干渠分水口相对较近的闸门开启时间早，距离远的由于渠道输水需要一定的时间，故闸门开启时间较晚。

根据优化调控模型计算结果，以d为单位，生成优化调控方案见图8，条形图代表各典型节点闸门开启和关闭的时间。

图8 6月上旬灌溉的各渠道配水过程Fig.8 Water distribution process of irrigation channels in early June

从图8可以更明显地看出，骨干渠系各个渠道闸门的开启时间与关闭时间，一分干、二分干、五支渠、三支渠、四支渠，由于距离渠首闸门较近，在渠首闸门开启的一天之内相继开启，一支渠和二支渠由于距离渠首闸门较远，均在4.67 d的时候，才进行开启。根据控制面积大小及渠道过水断面的限制条件，优化得出二分干、四支渠闸门在7 d左右关闭，五支渠闸门在9.29 d的时候关闭，总干渠、一分干、三支渠闸门在接近12 d的时候关闭。在渠首闸门关闭的时候，一支渠、二支渠的灌溉需求还未得到满足，不过由于一支渠、二支渠距离渠首闸门较远，渠首闸门关闭的时候，通向一支渠、二支渠的渠道中还有存量的水，这部分水会继续推进到一支渠、二支渠中，故一支渠、二支渠关闭时间比渠首闸门关闭的时间晚。

将本研究优化调控方案和灌区传统的配水方案的配水时间与配水时段内的弃水量进行对比分析。该灌区传统的配水方案，即是按照人工观测经验进行闸门的开启，待渠道控制灌溉面积的灌水量满足作物的灌溉需求后关闭闸门，没有进行优化配置。本研究调研获取了该灌区多年的灌溉闸门开闭时间方案，由此方案和计算出的优化调控方案进行对比分析：

（1）优化调控方案与灌区传统配水时间对比分析。将关键网格节点的优化调控方案和传统配水方案的配水时间，绘制柱形图如图9所示。

图9 关键网格节点配水时间对比图Fig.9 Comparison of water distribution time of key grid nodes

从图9中可以看出，在流量相同的前提下，与灌区传统配水方案相比，优化调控方案的配水时间均有明显缩短，总干渠的配水时间从15 d缩短到了12 d，缩短了3 d的时间；一分干的配水时间从13 d缩短到了11.91 d，缩短了1 d多的时间；二分干从10 d缩短到了7 d，缩短了3 d；其他一至五支渠配水时间也都有不同程度的缩短。

这是由于优化调控方案缩短了灌溉周期，增大了过水流量，能够保证水流快速通过渠道进入田间滴灌系统，保障作物关键生长期用水需求。

（2）优化调控方案与灌区传统配水弃水对比分析。在配水时段内，将关键网格节点的优化调控方案和传统配水方案的弃水量，绘制柱形图如图10所示。

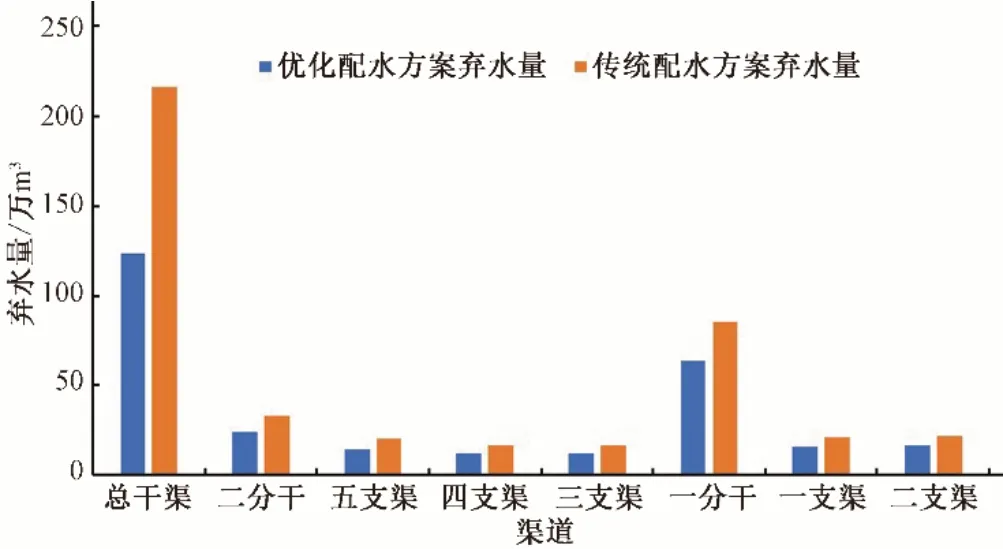
图10 关键网格节点弃水量对比图Fig.10 Comparison of discardedwater of key grid nodes

从图10可以看出，在配水时段内，干支渠优化配水方案的弃水量普遍少于传统配水方案的弃水量。对总干渠而言，传统配水方案的弃水量为216.30 万m3，优化配水方案的弃水量为123.6 万m3，减少了92.7 万m3；一分干传统配水方案的弃水量为85.2 万m3，优化配水方案的弃水量为63.9 万m3，减少了21.3 万m3；二分干传统配水方案的弃水量为33.0 万m3，优化配水方案的弃水量为23.76 万m3，减少了9.24 万m3；其他一至五支渠的弃水量也都有不同程度的减少。

这是由于传统的灌溉方案是凭经验观察田间灌水够了，才关闭闸门，而水流是一个过程，田间灌水够了的时候，渠道里还有很多存量的水，便会产生很多弃水，所以输配水系统是需要根据优化调控方案的计算结果提前关闸门的。因此，本研究提出的优化调控方法能够在配水时段，满足灌溉需求的前提下，减少无效弃水。

3.3 调控模式

上述模拟计算是针对6月上旬的用水需求，如果用水需求发生变化，比如4月上旬，只有小麦和棉花需要灌溉，红枣则不需要灌溉，即需要重新模拟计算，得到对应于用水需求的配水计划。以棉花、红枣、小麦滴灌灌溉制度为基础，根据实际情况，确定需要灌溉的水量。本研究将根据该灌区各个时期的灌溉需水量，利用软件模拟与优化，提前生成调控方案，在实际灌溉的时候可以根据用水需求，选取需要的灌溉方案。

针对上述灌区，本研究模拟计算出各种不同需水量对应的优化调控方案，形成该灌区输配水系统优化调控模式见表3。

表3中闸门开启时间和闸门关闭时间分别是指从本次灌溉总干渠引水闸开启开始计时，各渠道分水闸从第几分钟开始开启的，从第几分钟需要关闭。空白的地方是本次灌溉不需要开闭的闸门。以4月上旬的灌溉为例，需要灌溉棉花和玉米，红枣在4月上旬不需要灌溉。总干渠闸门从第0分钟开始开启，也即从总干渠闸门打开的时刻开始计算本次灌溉的时间，到第6 197分钟关闭，总干渠闸门本次灌溉一共开启6 197分钟；一分干分水闸从第21分钟开启，到第4 714分钟关闭，一分干分水闸本次灌溉一共开启4 693分钟。二支渠和五支渠因为种植的作物是红枣，不需要本次灌溉，闸门也不需要开启。

本研究提出的兵团某灌区输配水系统优化调控模式可为该灌区全年不同时期的灌溉调控提供依据，在实际灌溉中，可以此模式为基础，根据实际情况稍作调整即可。

以此类推，对于其他灌区，都可以采用同样的方法，利用软件建模、网格剖分、数值模拟，生成各种不同用水需求的调控方案，形成针对不同灌区的输配水系统优化调控模式，为灌区全年不同时期的灌溉调控提供依据。

4 结 论

针对兵团先进的田间高效节水新技术对应着低水平、粗放型的运行管理，输配水已不能满足作物在滴灌模式下的灌溉需求问题，本研究借助一维圣维南方程，在准确合理地模拟渠道系统水流运动过程的基础上，建立以灌水时间短、弃水少为控制目标的优化调控模型，并研发了相应的计算软件。在兵团某中型灌区进行了实例应用，构建了渠系拓扑模型，建立了渠系输配水优化调控模型，结果表明，该模型可以准确模拟渠系中某一次灌水的水流运动过程，生成输配水优化调控方案。经过与传统配水方案对比可知，优化调控方案缩短了灌溉周期，能够保证水流快速通过渠道进入田间滴灌系统，保障作物关键生长期用水需求，且在配水时段，满足灌溉需求的前提下，减少无效弃水。在此基础上，提出了适用于该灌区的输配水调控模式。

5 结 语

前人针对灌区渠系调度的研究多是静态的配水，本研究基于水动力学模型，将渠系输配水过程进行了精准模拟，且前人研究多针对地面灌溉，本研究针对具有高可控性和精准性的滴灌，与地面灌溉不同，滴灌灌溉制度具有高频性、灌溉周期短的特点，更需要严格按照作物的生长期按时按量进行灌溉。本研究针对滴灌系统将渠系输配水过程进行了动态模拟，以灌水时间短和弃水少为控制目标，建立了渠系输配水优化调控模型，计算出的优化调控方案，更符合实际水流情况，提高了闸门开闭时间的准确性，更符合滴灌系统高控制性的特点，且提出的灌区输配水调控模式为全生育期灌溉输配水调控提供了依据。