考虑配电网负荷的电动汽车分布式充电控制 *

吴忠强，张长兴

（燕山大学电气工程学院，秦皇岛 066000）

前言

由于化石燃料不是可再生能源，以及其燃烧产生的温室效应会带来许多负面影响，近年来插电式电动汽车（plug-in electric vehicle，PEV）作为新能源的产物正在逐步替代传统的燃油汽车［1］。PEV 在续航方面不像传统燃油汽车一样方便快捷，为应对这一问题，一方面是在提升电池容量方面取得进展［2］，另一方面需要大规模建立PEV 充电站。然而随着大规模PEV 接入电网，其将成为配电网的重要负载之一，如果PEV 无序接入电网可能对配电网的运行产生负面影响［3-5］，如使配电网的峰谷差增大以及造成用电高峰期的超负荷运行等。

近年来缓解配电网负荷的研究主要分为集群调度、车车协作以及上层优化3 个方面。集群调度主要以大规模PEV 作为灵活负载［6-11］，使其既作为储能设施，又作为能耗设施，在用电低谷期储蓄电能而在用电高峰期为充电站供给电能。车车协作主要通过车与车之间的充放电间接调节配电网的负荷［12］。上述方法都需要用户的高度配合以及需要PEV 具有放电功能，短时期内实现难度较大。上层优化方法通过控制充电站的供给来缓解配电网的运行压力，它只须考虑电网公司与用户之间的利益，而不依赖用户的配合，然而这一方法由于其供给不足，不能满足所有车辆都按照期望功率充电的需求，因此须设计下层的优化方案来满足整体用户的要求。对于下层最优充电的研究主要有集中式和分布式两种方法。集中式方法通过一个中央控制器，根据每辆PEV 的参数集中计算得到每辆PEV 最优充电功率［13-14］。然而集中式方法的缺点在于充电成本高，对基础电网设施要求高，在面对大规模车辆接入时，会因其计算量大而导致响应速度慢甚至出错，且这种集中处理的方法对单点故障没有调节能力。

针对集中式方法存在的缺点，分布式充电方案成为近年来研究的热点。分布式方案有以下优点：①可扩展性强；②通信成本低；③容错率高；④即插即用。文献［15］中根据功率分配过程中充电功率增量的不同，提出了一种分布式控制策略，通过控制车辆的充电功率增量来实现最优充电。文献［16］中针对混合动力PEV 提出了一种分布式协同充电控制算法，利用充电站的对等通信能力，在充电的每个时刻都能找到最优的充电策略。文献［17］中提出了一种分布式无初始化最优充电功率分配策略，该策略采用一种分布式算法来解决PEV 充电功率分配问题。文献［18］中PEV 充电问题被表述为一个广义纳什均衡博弈，使每辆PEV 在给定其充电需求和充电设施约束的情况下充电成本最小。以上文献只研究了下层的最优充电问题，并没有考虑上层配电网的实际情况。

针对上述问题，提出了一种考虑配电网负荷的电动汽车分布式一致性最优充电策略。本文的贡献如下：考虑电网波动以及充电站的需求建立了上层PEV 有序充电模型；建立了考虑整体用户满意度的下层PEV 最优充电模型，在多智能体框架下，提出一种分布式优化协议求解PEV 最优充电功率；仿真验证了本文模型和方法的有效性。

1 系统模型的建立

1.1 上层PEV有序充电模型的建立

由于大规模PEV 无序接入会增大配电网的负荷波动，存在充电站功率需求与用户功率需求的矛盾，对此提出2 层优化模型。上层以减少配电网负荷波动与满足充电站功率需求为目标，在减小配电网负荷波动的同时提前为下层制定最优负荷曲线。由于减小负荷波动会导致充电站功率不能满足所有用户的需求，因此下层以提高整体用户的满意度为目标建立优化模型。

PEV 的起始充电时间和所需的电量是确定充电站每个时间段所需负荷的基础。把一天平均划成T个时间段，每个时间段为15 min。PEV 用户大多是为满足日常的上下班和其他出行，少数PEV 的电量需求和起始充电时间分布可能无规则。但根据美国家庭出行调查（national household travel survey，NHTS）显示，规模化PEV所需电量服从N(0.5，0.12)分布，充电起始时间服从N(17.6，3.42)分布［19］。根据上述分布，利用蒙特卡罗方法对大规模PEV 无序充电进行模拟研究，可得到无序充电时充电站在不同时刻所需的功率。充电站在第i个时间段的功率需求可以表示为

若各时段充电站的功率需求和其他电力设施的功率需求在用电高峰期和低谷期叠加，将导致配电网在用电高峰供不应求，在用电低谷电能得不到高效利用。为使配电网在最大效益下安全运行，在考虑用户充电需求的同时，以减少配电网负荷波动与满足充电站功率需求为优化目标，建立目标函数如下：

1.2 下层PEV最优充电模型的建立

在1.1 节中以减少配电网负荷波动与满足充电站功率需求为目标，建立PEV 有序充电模型。在该模型下，可能产生充电站功率不能满足PEV 需求的问题，为解决此问题须建立PEV最优充电模型。

1.2.1 电池模型

因主要研究负荷分配问题，电池模型采用等效电路模型，其状态方程如下：

1.2.2 充电优化目标函数的建立

充电优化的最终目的是提高整体用户对充电情况的满意程度。用户的满意程度主要表现在PEV充电所花费的费用以及在期望的充电时间内PEV的SOC情况。稳定的充电功率有利于延长电池的使用寿命，因此在得到理想电量的同时也要保证小的功率波动。由式（7）可知，充电电流是影响功率波动的主要因素，因此以减少充电电流波动为目标，建立如下目标函数：

式中Gk为重构后第k辆PEV的性能指标函数。

1.2.3 目标函数的可行性分析和重构

由1.2.2 节可知，需要在式（16）不等式的限制下，由式（15）的目标函数求解出变量Pv，k。式（16）不等式的限制可通过定义如下罚函数来消除［20］。

2 算法设计与收敛性分析

2.1 算法设计

首先，针对1.1 节中建立的PEV 有序充电模型，采用粒子群优化算法求解式（2）的最小值，得出配电网每个时间段分配给充电站的功率Pia。然后，针对1.2 节中建立的最优充电模型式（19），求解PEV 最优充电功率。根据等微增量原理，由式（19）求解PEV最优充电功率可等效为使PEV充电功率增量一致，可通过设计分布式一致协议求解。每辆PEV 充电功率的增量可以表示为

双层优化模型架构如图1 所示。图中给出上层优化过程以及下层单个智能体执行一致性协议的流程和信息交互。该协议是分布式的，只需要每个智能体与其相邻的智能体交互。

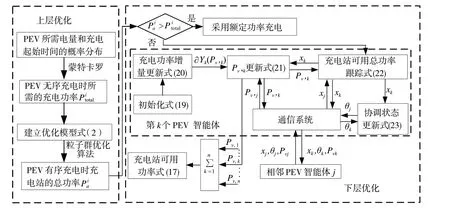
图1 双层优化模型以及单个智能体的信息交互流程

2.2 收敛性分析

2.2.1 一致性协议实现功率平衡

为方便证明一致性协议可实现功率平衡，结合图论知识［21-22］，将式（21）～式（23）写成紧凑的矩阵形式：

2.2.2 一致性协议可得到最优解

下面证明执行式（24）～式（26）的一致性协议，式（19）的目标函数可以收敛到最小值，进而得到优化问题的最优解。

定理1 如果α、β、γ满足：

式中ξ∈∂Y(Pv)接下来证明在新的坐标下，系统最终收敛到充电问题的最优解。

定义一个Lyapunov函数为

若式（33）成立，则式（42）小于0，那么M∈R3×3是负定的，由式（41）可知V̇＜0，系统渐近稳定，意味着系统轨迹收敛到最优充电问题的解。

3 仿真与结果分析

以居民小区100 辆PEV 为研究对象，系统的拓扑图如图2所示。图中箭头表示通信方式。

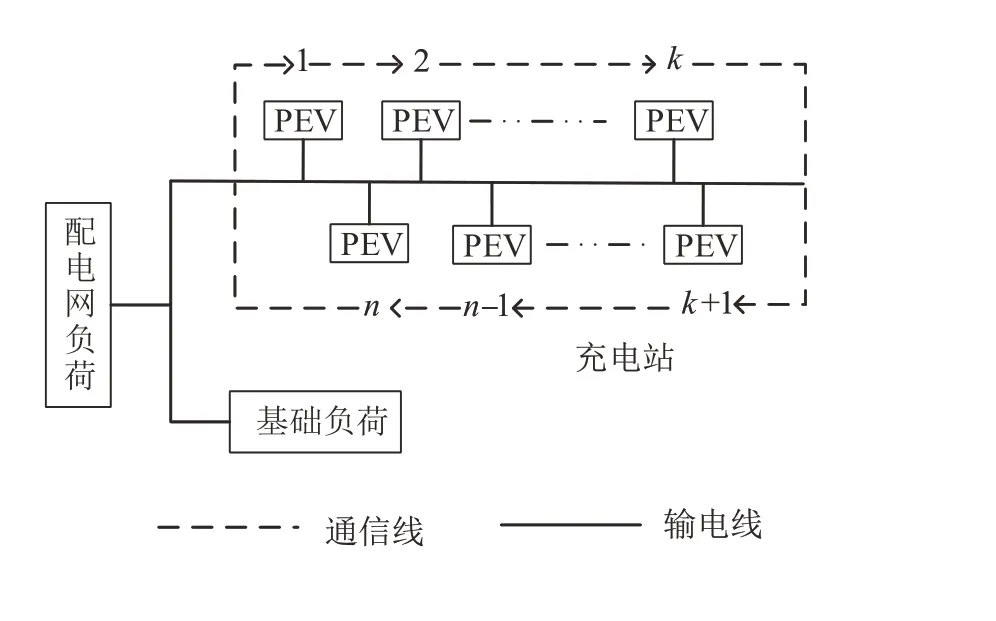
图2 系统拓扑图

图中n是可接入充电站的PEV 数量，各PEV 之间的通信是有向的。系统的仿真参数如表1所示。

表1 系统的仿真参数

表1 中ωmax、ωmin、c1和c2分别是粒子群优化算法中的惯性权重最大值、惯性权重最小值和学习因子。在Matlab/simulink 中搭建模型进行仿真验证，Simulink仿真模型如图3所示。

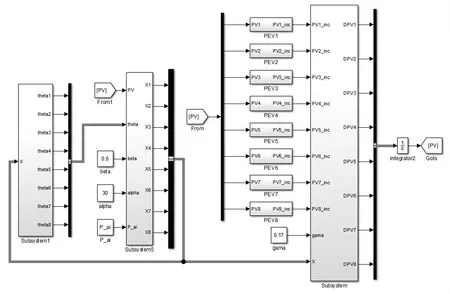
图3 Simulink仿真模型

3.1 上层PEV有序充电验证

给出配电网的基础负荷曲线，如图4所示。

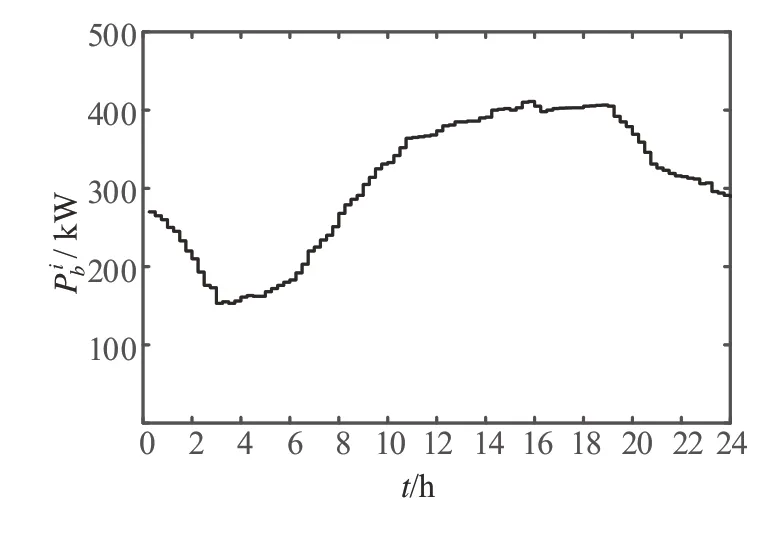
图4 基础负荷曲线

设100 辆PEV 所需的电量满足N(0.5，0.12)分布，起始充电时间满足N(17.6，3.42)分布，通过蒙特卡罗方法得出的无序充电时充电站的功率变化曲线如图5所示。

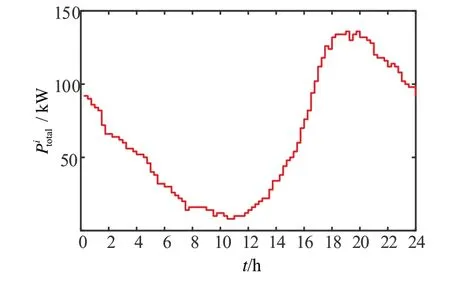
图5 无序充电时充电站的功率变化

经过优化后得到的有序充电时充电站的功率变化曲线如图6所示。

图6 有序充电时充电站的功率变化

为便于比较配电网的功率变化，给出有序充电和无序充电时配电网的负荷曲线如图7所示。

表2 给出图7 中有序充电和无序充电时配电网负荷变化的比较。

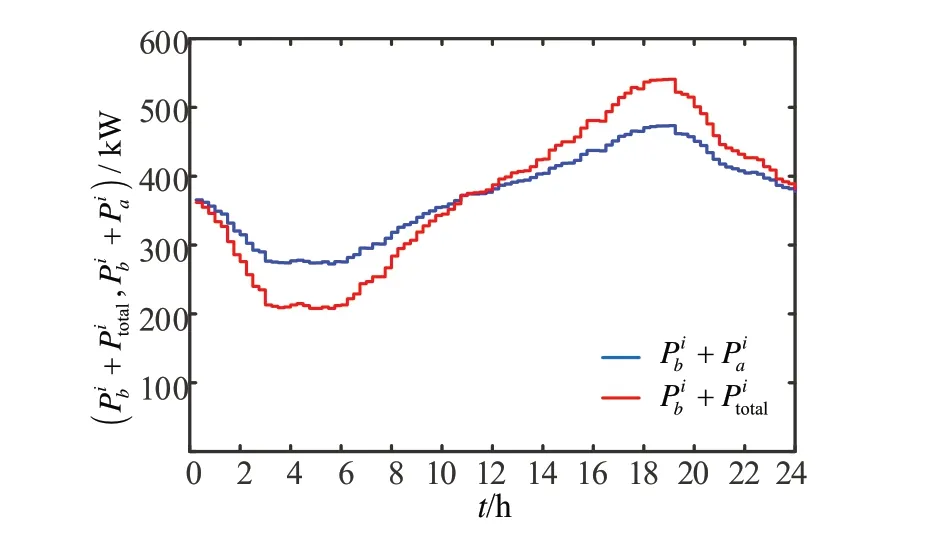
图7 有序充电和无序充电时配电网的负荷曲线

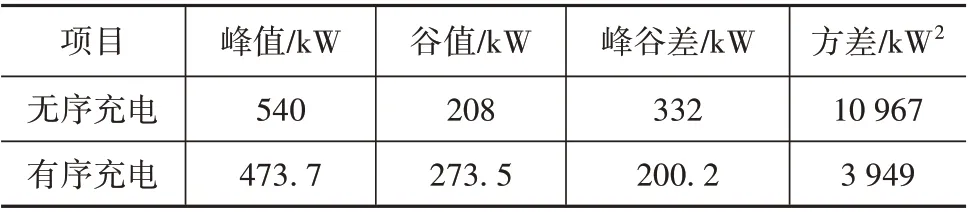
表2 有序充电/无序充电时配电网负荷变化的比较

由表2 可看出，有序充电时配电网负荷变化的峰谷差为200.2 kW，比无序充电时降低了39.6%，有序充电时配电网负荷变化的方差为3 949 kW2，比无序充电时降低了177.7%。结果表明，在经过优化后得到的PEV 有序充电时配电网负荷的峰值降低，谷值增加，且波动减小。

3.2 下层PEV最优充电验证

设有9 辆PEV 参与验证，其电池参数如表3所示。

表3 PEV电池参数［15］

（1）验证所提分布式方法在PEV 有序充电环境下的有效性

假设在10：00 时有8 辆PEV 接入充电站，此时充电站的可用充电功率为16 kW。研究利用所提协议为其充电的情况。图8 给出PEV 充电功率的变化过程。图9给出充电消耗总功率∑Pv，k的变化过程。图10 给出1 h 的PEV 功率变化过程。图11 给出充电站功率供需变化ΔP的变化过程。

由图8 可看出，PEV 的功率在12 s 内收敛到最优充电功率。由图9 可看出，当接入的车辆均收敛到最优充电功率时，总的消耗为可用总功率16 kW，此时供需平衡。图10 给出1 h内PEV 充电功率变化情况。因在上层中，每隔15 min 更新一次充电站功率，所以充电站功率是时变的。由图10 可看出，充电站总功率经历了16、14、14.5 和16 kW 4 次变化，在每次变化后充电功率都能收敛到最优充电功率。由图11 可看出，在充电站以恒功率运行时，其供需始终保持平衡，当功率发生改变时，所提方案也能通过车辆之间的相互协调快速恢复供需平衡。

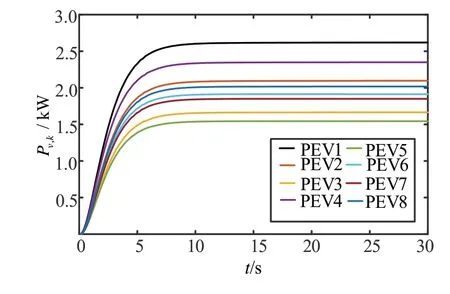
图8 PEV充电功率变化

图9 充电消耗总功率变化

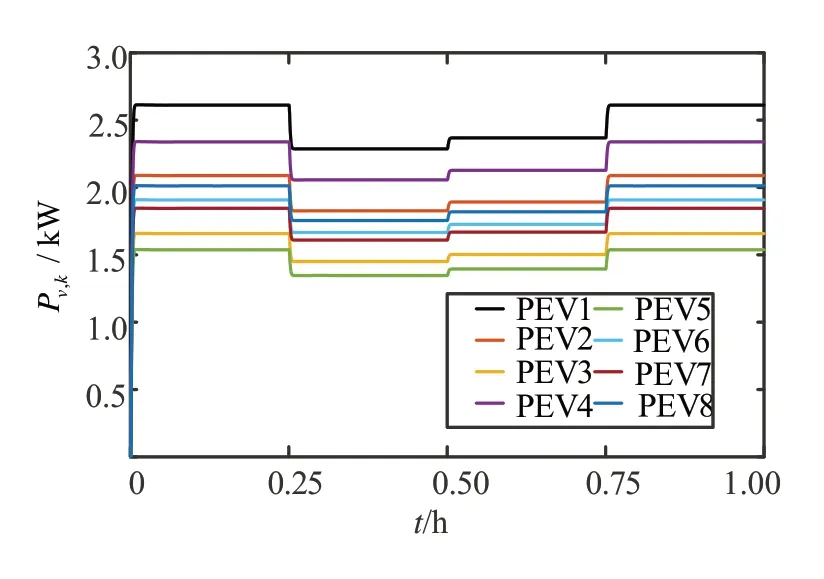
图10 1 h的PEV充电功率变化

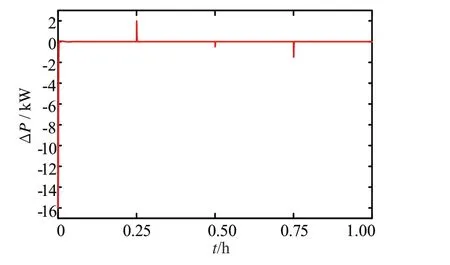
图11 充电站功率供需变化

（2）鲁棒性及即插即用性的验证

假设在200 s 配电网功率发生波动，此时充电站的功率也受到影响，首先验证发生小幅低频波动时的情况。假设总供给功率由16 kW 变为（16+sin（0.02t））kW，且在 功率波动期间PEV9 接入（500 s），此时的PEV 充电功率变化情况如图12 所示。然后验证发生大幅高频波动时的情况，假设总的供给功率由16 kW 变为（16+2sin（0.05t））kW，其他条件与发生小幅低频时一样，此时PEV 充电功率变化情况如图13 所示。图14 和图15 分别给出两种情况下充电站功率供需变化情况。

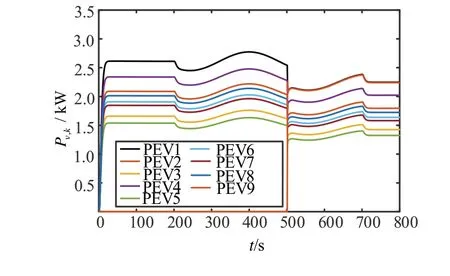
图12 波动为sin（0.02t）时PEV充电功率变化

由图12和图13可以看出，无论充电站功率发生小幅低频波动还是大幅高频波动，PEV 充电功率都始终收敛在最优值，且在PEV9 接入后，采用所提的一致性协议都很快收敛到最优值。由图14 和图15可以看出，发生小幅低频和大幅高频波动时，供需不平衡的波动幅度分别在5.2%和12.5%以内，且均在8 s内达到供需平衡，证明了所提的分布式协议具有很强的鲁棒性。

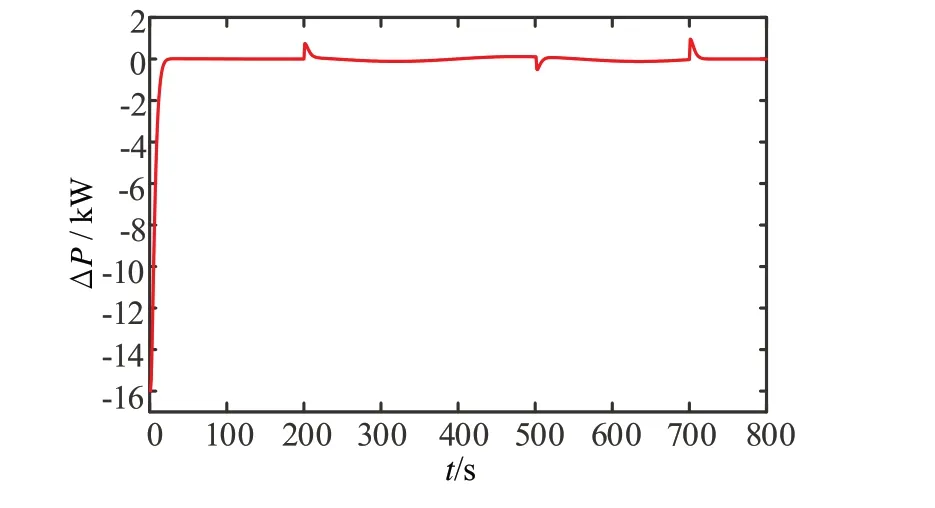
图14 波动为sin（0.02t）时充电站功率供需变化

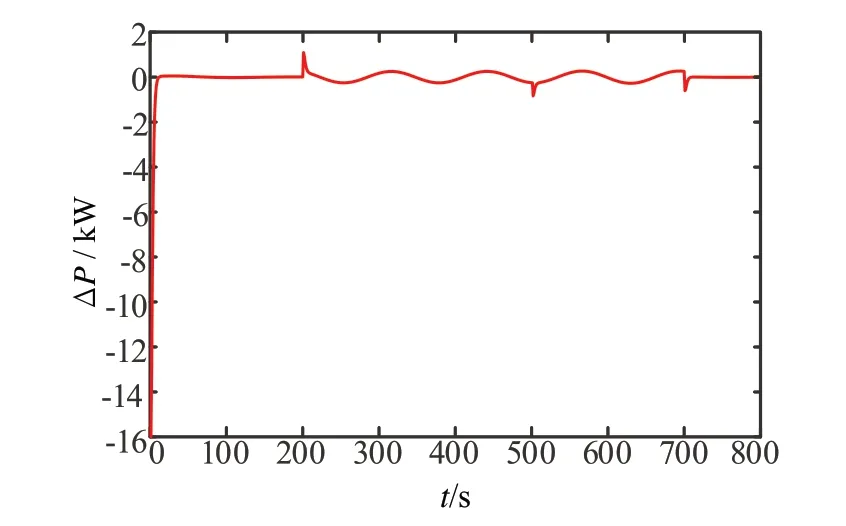
图15 波动为2sin（0.05t）时充电站功率供需变化

（3）可扩展性的验证

在充电高峰期，接入的PEV 车辆较多，验证所提方案的可扩展性，即验证所提方案在PEV 充电高峰时期能否正常运行。假设在16∶00时有20辆PEV接入，此时充电站的可用功率为40 kW，在1∶00时有50 辆PEV 接入，此时充电站的可用功率为100 kW。图16 和图17 分别给出这两个时刻PEV 充电功率变化，图18和图19分别给出这两个时刻充电消耗总功率∑Pv，k的变化。

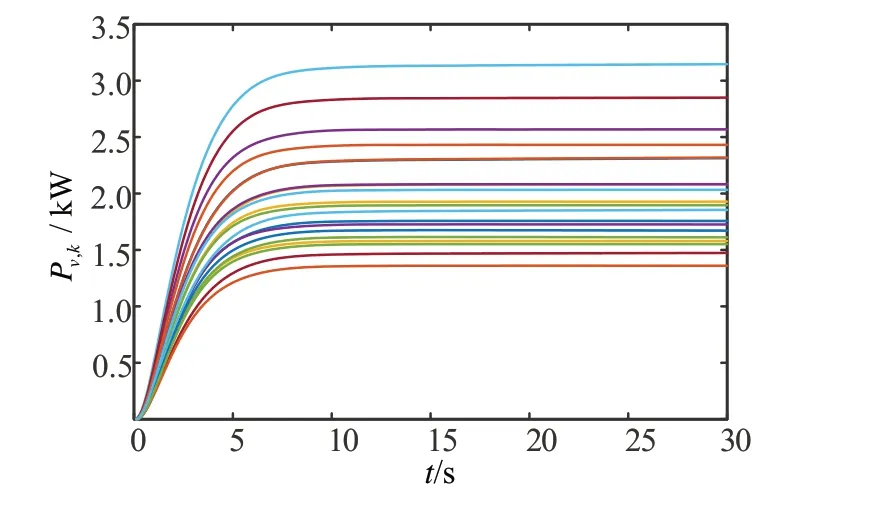
图16 20辆PEV接入时充电功率变化

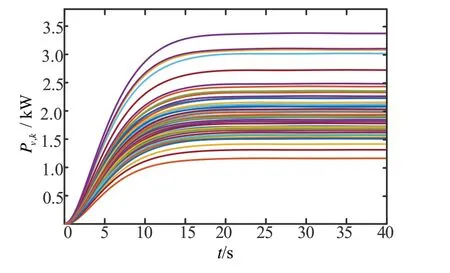
图17 50辆PEV接入时充电功率变化

图18 20辆PEV接入时充电消耗总功率变化

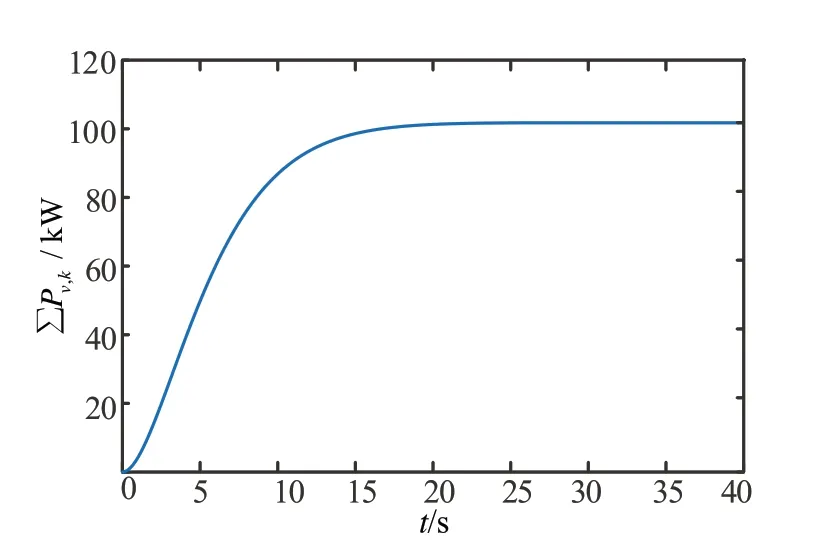
图19 50辆PEV接入时充电消耗总功率变化

由图16和图17可看出，20辆PEV 接入时在13 s内均收敛到最优充电功率；50 辆PEV 接入时在20 s内均收敛到最优充电功率。由图18和图19可看出，在车辆收敛到最优充电功率时，总可用充电功率分别收敛到40和100 kW，表明所提分布式协议具有很好地可扩展性。

（4）分布式算法的性能比较

为体现所提出的基于动态平均一致性算法的分布式协议的优越性，与基本一致性算法进行比较。与9 辆PEV 参与验证时的情况相比，其PEV 充电功率变化情况如图20所示，图21给出对应的情况下充电站总功率的变化。

图20 PEV充电功率变化

图21 充电消耗总功率变化

4 结论

研究采用双层结构的PEV 有序充电和最优充电问题。所得结论如下：上层将PEV 作为配电网的灵活负载，以减少配电网负荷波动与满足充电站功率需求为目标建立优化模型，并采用粒子群算法求解不同时间段配电网分配给充电站的功率，解决PEV 有序充电问题；下层以减少充电电流波动为目标建立优化模型，提出一种基于多智能体的分布式一致性协议，解决PEV 的最优充电问题，所提方案不需要中央处理器，只需要相邻车辆之间相互协调，且无须初始化过程，具有即插即用性、可扩展性和鲁棒性。所提出的双层优化方案既减小了配电网峰谷差以及负荷波动，又满足了PEV 用户整体需求。仿真验证了方案的可行性。