基于改进径向基网络的电动舵机滑模控制

李冬辉,王立献,周 满,3,江华侨,曹晓鹏

(1.天津大学 电气自动化与信息工程学院, 天津 300072;2.宁波帅特龙集团有限公司, 浙江 宁波 315000;3.中国科学院 长春光学精密机械与物理研究所, 长春 130033)

0 引言

电动舵机作为飞行器的主要执行机构,对飞行器的机动性、打击精度等有着决定性的作用,其性能决定着飞行器的静态及动态性能[1-2]。然而,电动舵机系统中不可避免的存在间隙、摩擦等非线性环节,导致小角度跟踪时出现平顶问题,严重影响舵机系统的跟踪精度[3-5],甚至引发弹道发生极限环震荡。在跟踪精度要求不高的情况下,通过提高加工、装配精度等,传统的PID控制能满足系统指标要求。但随着国内外市场竞争加剧,飞行器性能指标飞速提升,其对电动舵机伺服系统提出更高的指标要求,传统的PID控制理论已经很难满足电动舵机高精度、高动态性能的需求[6]。

为了补偿非线性摩擦对机电伺服系统性能的影响,Lin等提出了一种基于LuGre模型的自适应滑模控制器,在线估计滑模面参数,并取得较好跟踪效果[7],但滑模控制器自身存在抖振问题,容易引发系统谐振,破坏系统的稳定性,影响其工程应用[8-9]。Li等为了满足现代高性能飞机的需求,提出了模糊PID控制策略,该控制策略综合了模糊控制和PID控制的优点,对时变复杂系统具有较好的适应性[10]。但模糊PID控制器存在量化因子和比例因子等参数的选取过于依赖经验、参数固定等缺点[11]。自抗扰控制器可以较好的解决电动舵机非线性等问题,为此张明月等,提出了自抗扰控制器,较好的提高了电动舵机系统的动态响应及自适应性能,但其参数整定过程较为复杂[12]。近年来,智能控制理论因其对扰动具有较强的自适应能力而受到广泛关注,如遗传算法[13]、蚁群算法[14]、BP神经网络[15]等,其中,径向基网络因其对未知项具有较强的逼近能力,在伺服系统上得到研究[16]。Liu等针对控制系统的非线性、时不变和不确定性等问题,提出了基于径向基网络的转矩控制算法,较好的提高了系统控制精度和鲁棒性[17]。针对位置伺服系统中的干扰及模型参数确定困难的问题,Li等提出了一种基于反演策略的径向基网络滑模控制策略,解决了外部扰动和模型不确定性问题,并取得较好的控制效果[18]。但智能算法计算复杂,工程实现难度大,尤其是飞行器舵机系统这种高实时性系统上应用难度较大[19-20]。综上分析,各类算法均存在一定的优势及不足,高精度、高动态性能的电动舵机控制策略仍有待进一步研究。

因舵机系统中的摩擦及间隙具有非线性且时变的特点,难以对其进行准确建模[21],而滑模控制对舵机非线性具有较强的自适应能力,同时径向基网络对未知项具有较好的逼近能力,可以较好的解决模型的不确定性,为此本文提出了基于RBF网络的滑模控制策略,对系统的确定部分采用滑模控制,对不确定部分采用RBF网络进行逼近。同时,为降低计算复杂度,使用2个参数近似替代权值矩阵,便于工程实现,进而提高系统的控制效果,削弱舵机系统的位置平顶。

1 电动舵机数学模型

1.1 电动舵机系统工作原理

本文中使用电动舵机主要包括三相无刷电机、减速器、编码器、电位计等,如图1所示。

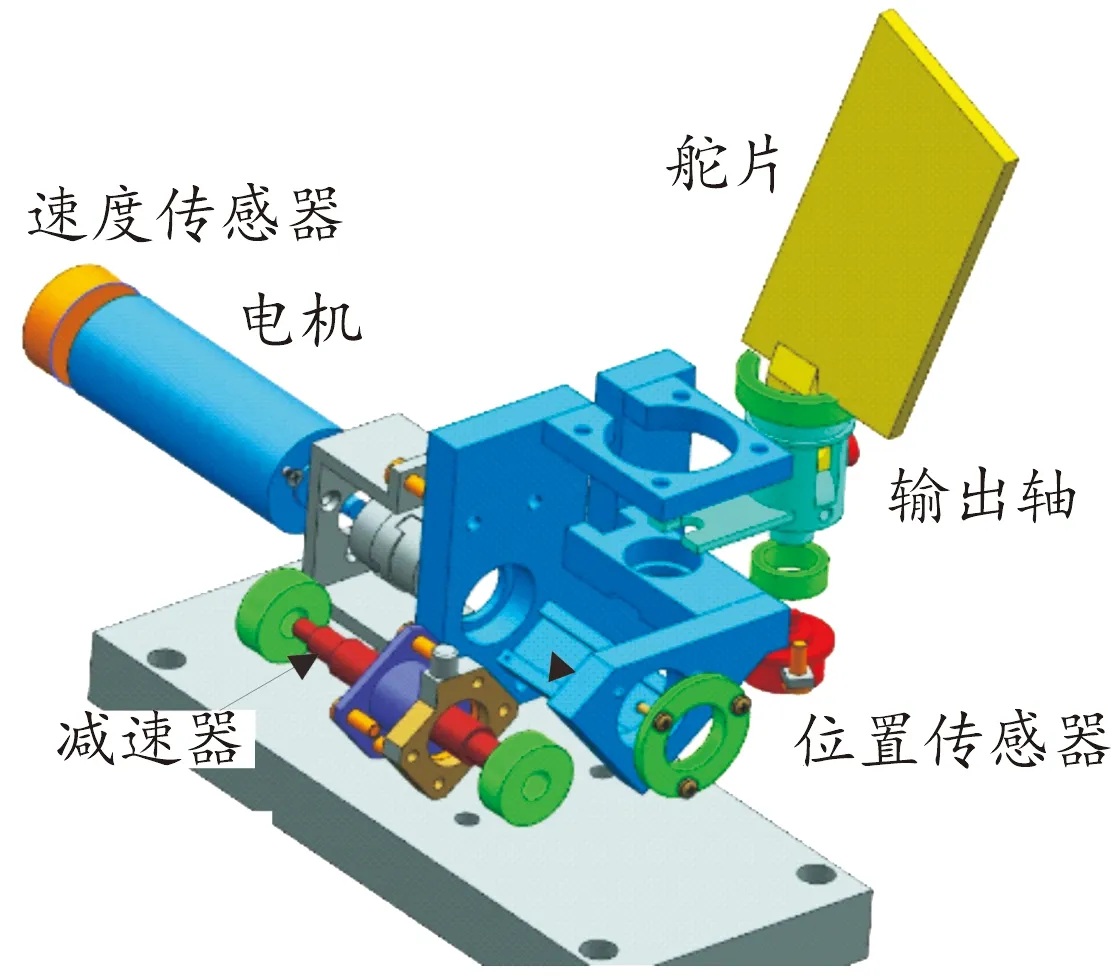
图1 电动舵机系统结构图Fig.1 Structure diagram of EMA system

编码器为速度传感器,与电机输出轴采用直连方式,可有效减小电机输出轴与编码器间的间隙。位置传感器与舵机的输出轴直连,实现位置闭环。电动舵机系统工作时,伺服控制器根据电动舵机角度及角速度误差等,计算得到相应的控制量,并驱动电机正反转,进而控制减速器旋转,并通过传动机构带动舵机输出轴的旋转,最终实现舵片的角度控制。

1.2 电动舵机数学模型

根据电机电压、力矩平衡方程、系统传动方程得到伺服系统动力学模型,舵机系统可以描述成如下形式:

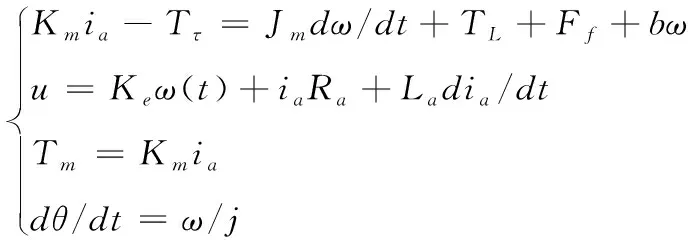
(1)

式中:Tτ为间隙扰动(N·m);TL为负载力矩(N·m);Ff为摩擦力矩(N·m);Ke为伺服电机的反电动势常数(V·s/rad);Km为电机的转矩系数(N·m/A);ia为电枢电流(A);Jm为电机的转子惯量(kg·m2);j为减速器的减速比。

令负载TL为零,可得到舵机系统传递函数为:

(2)

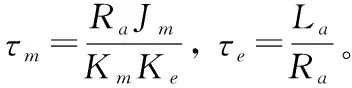
由于τe非常小,有τe<<τm,故可令τe=0,则电动舵机系统传递模型可描述为如下形式:

(3)

2 电动舵机平顶现象分析

由于间隙及摩擦等非线性因素影响,采用传统PID控制,电动舵机在跟踪小角度指令时存在明显的“平顶现象”,如图2所示。

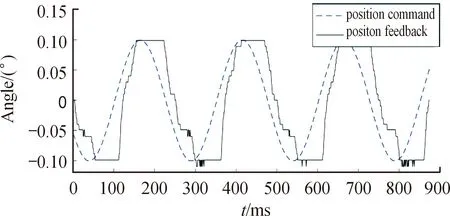
图2 位置跟踪平顶现象Fig.2 The phenomena of flat top

从图可知,位置指令0.1°、4 Hz时,平顶时间大约64 ms,位置跟踪误差为0.123°,严重降低了舵机系统对小角度正弦指令的跟踪性能。在舵效较低的情况下平顶问题对飞行器性能影响较小,但在舵效较高时 “平顶现象”导致飞行器弹道指令出现极限环震,弹道极限环震荡的频率为 10 Hz、幅值为0.25°,如图3所示。

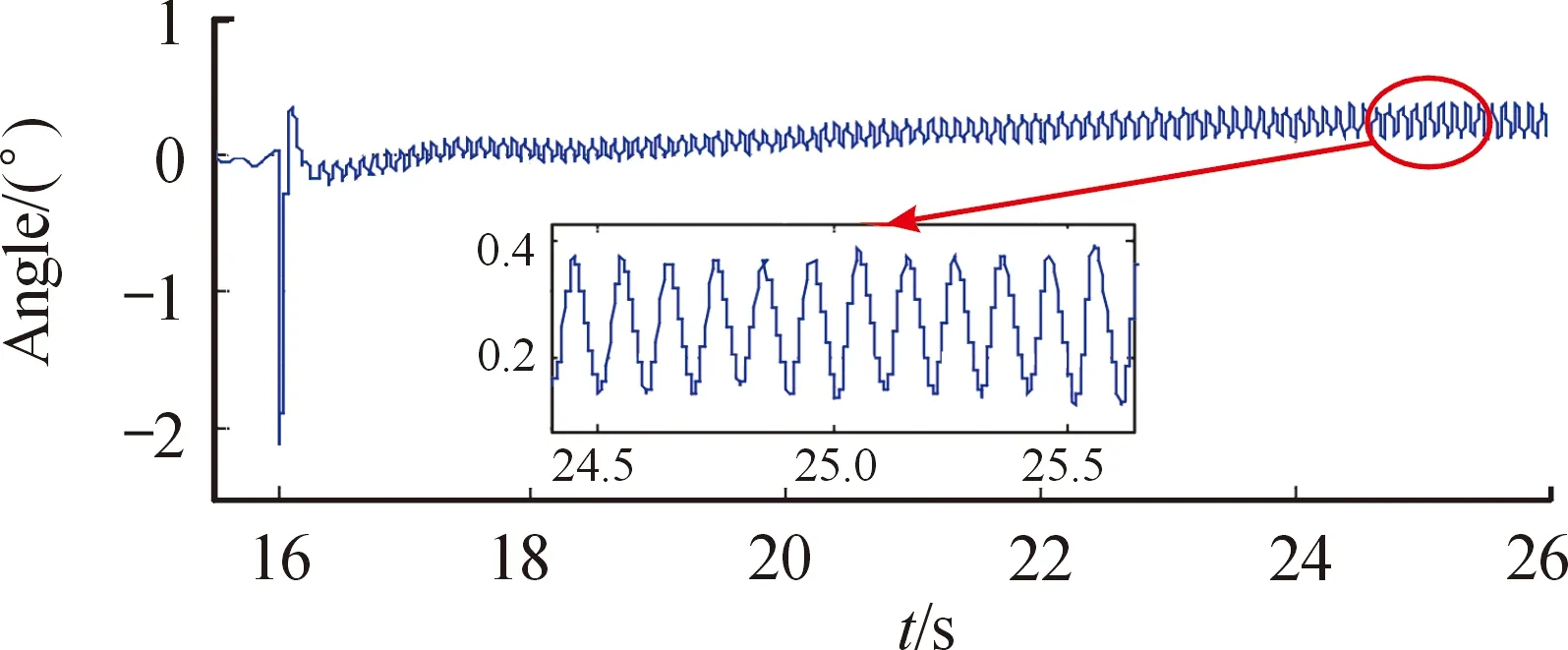
图3 弹道极限环震荡现象Fig.3 The phenomena of limit cycle oscillation

2.1 间隙对平顶问题的影响分析

间隙对舵机系统的影响如图4所示。“speedfeedback”为速度反馈,“positionfeedback”为位置反馈。从图可知,由于速度传感器直连在电机轴上,位置传感器直连在舵机输出轴上,由于传动机构的间隙影响,舵机速度在214 ms处换向,而位置反馈则在223 ms换向,即间隙环节引入了9 ms的延迟,这段时间电动舵机输出轴角度不变,形成位置平顶。

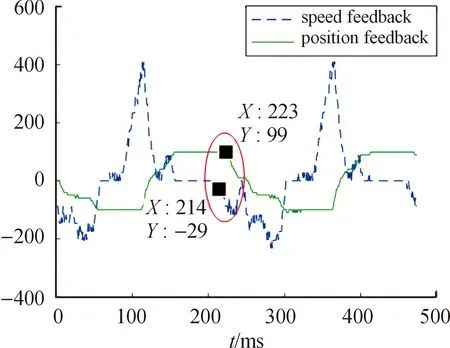
图4 间隙对舵机系统的影响Fig.4 The effect of backlash

2.2 摩擦对平顶问题的影响分析

舵机系统中的摩擦主要包括静摩擦和动摩擦,通常在小角度正弦指令的跟踪过程中,静摩擦力矩对舵机性能指标的影响更大,其对舵机系统的影响如图5所示。其中,“PWM”为控制量输出,“speedfeedback”为速度反馈。

图5 摩擦对舵机系统的影响Fig.5 The effect of friction

从图5可知,由于静摩擦力矩的影响,控制量输出一直处于非零状态,而156～213 ms速度反馈持续为零,即存在将近57 ms的速度死区,导致舵机输出轴位置固定不变。

综上可知,静摩擦为主要影响因素,因此,削弱摩擦非线性因素的影响,可快速、高效的削弱舵机系统的“平顶”现象。但受结构加工及装配精度、结构磨损等影响,舵机系统的间隙及摩擦是随位置、环境的变化而变量,难以精确测量或准确建立其非线性模型。为此,引入滑模控制提高舵机系统对非线性的鲁棒性,同时引入径向基网络对模型中不确定部分进行逼近,从而提高控制精度。

3 改进的RBF-SMC控制器设计

3.1 系统描述

对舵机模型进行反Laplace变换,

(4)

在实际工程应用中,由于结构加工精度、温度等因素影响,Ff、Tm、Tτ是实时变化的,难以精确测量,在控制器设计过程中,将其作为未知量进行设计。

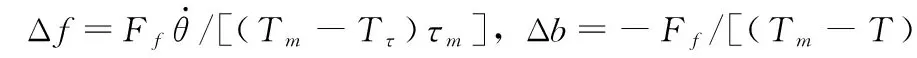
(5)

3.2 滑模控制器设计

设计滑模面为

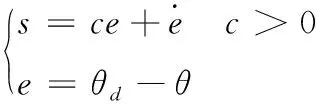
(6)

式中:e为位置跟踪误差;θd为位置指令角度;θ为位置反馈角度。

由式(5)、式(6)可得滑模控制律为

(7)

其中, sat(s)为饱和函数。

因舵机模型难以精确测量,尤其是摩擦、间隙等为时变的,难以准确测量,为此针对其中的未知不确定项,构建f*,b*代替f(θ,t)+Δf(θ,t)和b+Δb,即

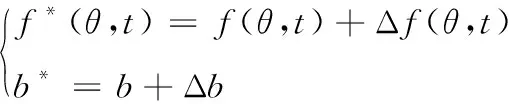
(8)

则滑模控制器的控制律可改写为:

(9)

因f*,b*为未知不确定项,且是时变、非常值,为此引入RBF网络对其进行逼近,提高补偿精度。

3.3 改进的RBF-SMC控制器设计

3.3.1改进的RBF控制器设计

RBF逼近算法为

(10)

式中:W*和V*为RBF网络理想权值;εf和εb为逼近误差;hf,hb为隐含层输出。

根据RBF逼近原理,采取高斯函数为激活函数,RBF网络输出为

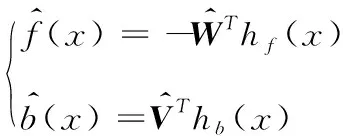
(11)

权值矩阵中的待估计参数较多,均需要进行迭代计算,计算复杂度较高,严重降低了处理器的计算效率。在电动舵机系统中,其处理器通常为C2000系列的DSP处理器,其处理能力有限,在保证舵机系统实时性的情况下,难以满足传统RBF控制器的计算要求。为此考虑使用2个单参数取代权值矩阵,待估的参数数量大幅缩减,迭代效率大幅提升,虽然会降低逼近效果,但滑模控制自身对参数波动具有一定的鲁棒性,因此不会对舵机系统的控制精度造成太大影响。

取正常数φ和ψ代替RBF网络的理想权值W*和V*,即:

(12)

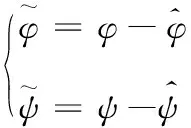
(13)

因为有

(14)

可得:

(15)

同理可得:

(16)

即,设计控制律为:

(17)

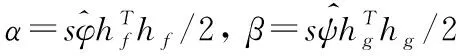
为保证系统的稳定性,直接令RBF权值预估值的最大值为权值估计,达到较好的补偿效果。

即有,

(18)

其中,εN和D分别为估计误差和扰动上界。

3.3.2稳定性分析

为分析所设计控制系统的稳定性,设计Lyapunov函数对RBF-SMC算法的稳定性进行验证。

对滑模面求导,

(19)

结合控制律对上式整理有,

d(t)-ηsat(s)-μs

(20)

定义李雅普诺夫函数为,

(21)

其中,γf>0,γb>0。

(22)

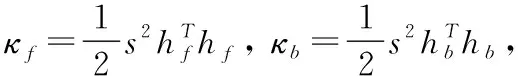
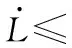
(23)

即有,

(24)

设定自适应律为

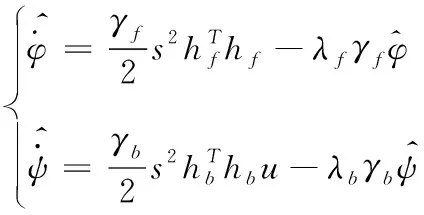
(25)

式中,λf=2μ/γf,λb=2μ/γb,同时满足γf>0,γb>0,μ>0。

则可得,

(26)

由于有:

(27)

同理可得:

(28)

对上式联立整理可得:

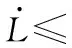
(29)

因为有λf=2μ/γf,λb=2μ/γb,γf>0,γb>0,μ>0,满足γf>0,γb>0,即有,

(30)

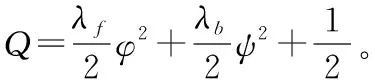
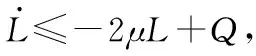
(31)

即有,

(32)

4 实验验证

为验证RBF-SMC控制算法的合理性,在电动舵机平台上进行算法验证,实验系统原理如图6所示。电动舵机实验平台主要包括电动舵机系统、CAN信号采集设备、数据处理分析系统、五轴转台等。

图6 电动舵机实验原理图Fig.6 Schematic diagram of experimental system of electromechanical actuator

基于图6的试验平台,在电动舵机系统上进行算法实现,并与PID控制算法进行对比试验。

4.1 正弦跟踪性能测试

为验证RBF-SMC控制算法在小角度下的跟踪性能,分别采用PID、RBF-SMC控制算法控制电动舵机跟随0.1°正弦指令,跟踪性能如图7所示。

如图7(a),“PID”、“RBF-SMC”分别为PID和RBF-SMC算法的位置反馈,“command”为位置指令。从图可知,在跟踪0.1°正弦舵偏指令时,RBF-SMC算法的优点得到凸现,采用PID算法存在较为明显的位置跟踪平顶,平顶时间约为64 ms,而RBF-SMC算法平顶时间为9 ms,平顶时间大幅缩减。如图7(b),“PID”为PID算法时位置跟踪误差,“RBF-SMC”为RBF-SMC算法位置跟踪误差,从图可知,PID位置跟踪误差为0.123°,RBF-SMC位置跟踪误差为0.04°。另外RBF-SMC控制算法存在轻微抖动问题。

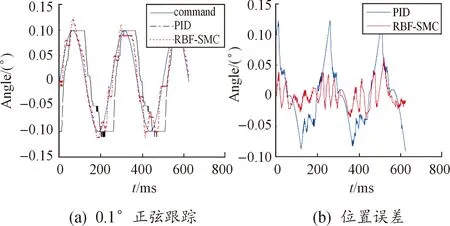
图7 0.1正弦跟踪性能对比图Fig.7 Comparison of 0.1 ° sinusoidal tracking performance

PID、RBF-SMC控制算法的正弦跟踪结果如表1所示。在跟踪小角度正弦指令时,RBF-SMC控制算法相比PID控制算法,可以显著提高位置跟踪精度,有效的缩减平顶时间。

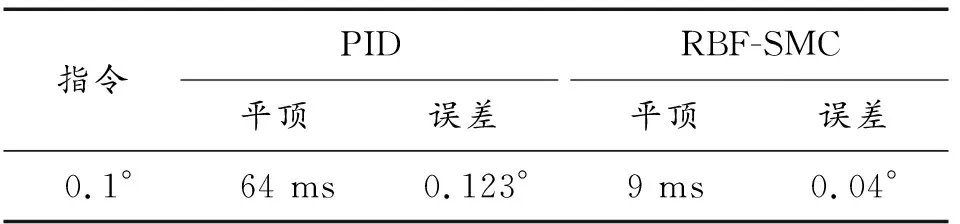
表1 PID、RBF-SMC控制算法的正弦跟踪对比Table 1 Tracking comparison between PID and RBF-SMC

通过上述实验,可知,采用RBF-SMC控制算法能提高电动舵机系统的位置跟踪精度,同时将小角度下的平顶时间从64ms缩减至9ms,但其缺点是仍存在轻微的抖动现象。

4.2 半物理联调测试

为验证飞行过程中电动舵机系统的性能,在不加入导引头的情况下,使用工控机、五轴仿真转台、电动舵机等系统进行半物理联调测试,模拟飞行器实际飞行过程。总体半物理联调测试中电动舵机系统的测试结果如图8和表2所示。

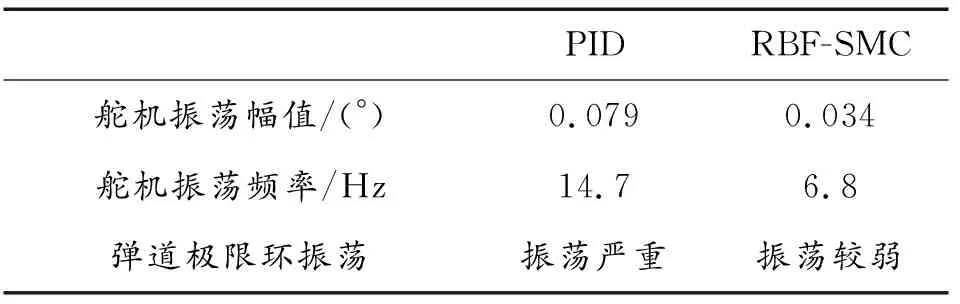
表2 弹道跟踪性能对比Table 2 Trajectory tracking performance comparison between PID and RBF-SMC

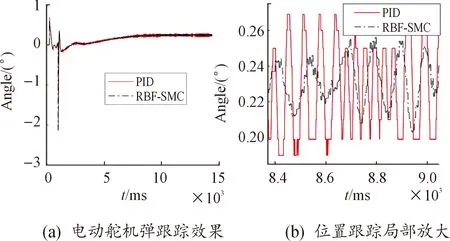
图8 总体半物理联调测试中电动舵机系统的跟踪效果图Fig.8 Tracking comparison of EMA system semi physical joint debugging

从图8(a)可以看到,2种控制算法均具有较高的响应能力,在大机动下,仍可以较好的跟踪弹道指令,无发散情况发生,但从图(b)可知,2种控制算法在弹道指令趋于稳定或弹道指令小角度波动情况存在较大差别。

从表2可知,PID控制算法存在幅值0.079°、频率14.7 Hz的等幅振荡,导致弹道出现极限环震荡现象,严重影响飞行器的飞行品质;RBF-SMC控制算法振荡频率有所降低为6.8Hz,其振荡幅值相比为0.034°,幅值及频率较小,与PID控制算法相比,不会破坏飞行器控制系统的控制性能。

从以上实验结果可以看出,相比于传统的PID控制算法,RBF-SMC算法能大幅减小位置平顶时间,提高小角度情况下的位置跟踪精度,同时能较好的抑制弹道抖振的问题。

5 结论

针对电动舵机小角度平顶现象引发到的弹道极限环振荡问题,本文对平顶现象进行了研究分析,并提出了改进的径向基滑模控制方法,利用滑模算法的强鲁棒性减小平顶时间,利用径向基网络对不确定项自动逼近,抑制滑模控制器抖振、提高跟踪精度。实验结果表明,与传统的PID控制算法相比,改进的径向基滑模控制算法在跟踪0.1°,4 Hz正弦指令时,平顶时间从64 ms缩减至9 ms,跟踪精度从0.123°提高至0.04°;半物理试验时,弹道最大抖振幅值从0.079°降低至0.034°,最大抖振频率从14.7 Hz降低至6.8 Hz,满足飞行试验要求。采用改进的径向基滑模控制方法可有效削弱小角度平顶现象,提高小角度控制精度,进而有效的削弱弹道抖振。但此算法仍存在不足之处,控制算法自身仍存在一定的颤振,弹道抖振现象也未完全消除,为此舵机控制器仍有待进一步研究,在提高跟踪精度同时消除抖振现象。