关于智能运维中KPI异常检测与预测的研究

陈云烁?符繁强

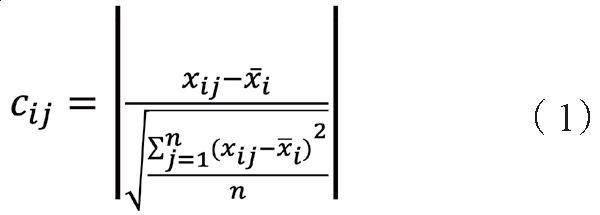
摘要：业务性能指标（key performance indicator，KPI）异常检测是网络智能运维中的底层核心技术，对网络故障发现和修复具有重要意义。针对智能运维中KPI异常检测和异常预测问题，使用数据特征分析、相关性分析、多元线性回归分析、机器学习等方法，分别建立KPI异常值检测差与标准差模型、KPI异常值预测多元线性回归模型、KPI异常值预测RBF神经网络模型（RBF—Radial Basis Function），并通过构建评估指标模型对模型预测的优劣进行判断，给出运营商基站KPI核心指标的异常孤立点、异常周期以及异常值预测。

关键词：异常检测；异常预测；差与标准差；回归模型；RBF神经网络模型

一、问题描述

异常检测（异常诊断/发现）、异常预测，是智能运维中首当其冲需要解决的问题[1]。这类问题是通过业务、系统、产品直接关联的KPI业务指标进行分析诊断，本文以运营商基站KPI的性能指标为研究数据，研究三项核心指标。

第一项指标：小区内的平均用户数，表示某基站覆盖的小区一定时间内通过手机在线的平均用户人数；

第二项指标：小区PDCP流量，通过小区PDCP层所发送的下行数据的总吞吐量（比特）与小区PDCP层所接收到的上行数据的总吞吐量（比特）两项指标求和到，表示某基站覆盖的小区在一定时间内的上下行流量总和；

第三项指标：平均激活用户数，表示某基站覆盖的小区在一定时间内曾经注册过无线网络的平均人数。

异常检测问题：利用提供的研究数据，判断所有小区的异常孤立点和异常周期以及时间周期的选择标准。

异常预测问题：根据检测出的异常值，建立异常值前的数据预测模型，分析预测未来是否发生异常数值。

二、模型假设

1.假设题中给定的数据真实有效；

2.假设提供数据中异常数据只存在少部分；

3.假设运营商基站所覆盖的区域恒定。

三、符号说明

符号及解释如表1。

四、异常检测问题模型的建立与求解

（一）异常检测问题分析

利用KPI性能指标对小区内的平均用户数、小区PDCP流量、平均激活用户三项关键指标分析异常检测问题。

将小区PDCP层所发送的下行数据的总吞吐量（比特）小区PDCP层所接收到的上行数据的总吞吐量（比特）两个指标进行整合得到小区PDCP流量，提取数据时间、基站编号、小区编号、小区内的平均用户数、小区PDCP流量、平均激活用户数进行数据重构。

引入差与标准差的倍数，用来分析异常值，定义：若数据差与标准差的倍数大于2倍以上，则该数据称为异常数据，判断三个关键指标的异常孤立点和异常周期。

（二） KPI异常值检测差与标准差模型

1.差与标准差的倍数

以小区内的平均用户数为例，计算出其对应的差与标准差的倍数，其余指标小区PDCP流量，平均激活用户按照相同方法操作。

其中，表示第个小区第个数据的差与标准差的倍数，表示第个小区第个数据的值，表示第小区指标平均值，=1，2，3，…，58。=1，2，3，…，。

2.异常值与非异常值判断

其中，表示异常值的判断值，表示异常值，表示非异常值。

（三）时间周期分析

由于数据中提供的小区个数多、时间跨度长，本文随机选取三个小区9天的数值作为展示，分别选取260190015、26019039、26019057小区的三个核心指标数值作数据可视化处理分析其周期性。

通过指标可视化分析图观察可知三个小区关键指标均存在异常值，针对不同场景的运维虽然会混合多个时间间隔的数据，但具备时序性特点，均为随时间变化而变化。小区内的平均用户数小区、平均激活用户、PDCP流量三项核心指标呈上下起伏的周期变化，为此选取小区内的平均用户数、小区 PDCP流量、平均激活用户数时间周期均为1天。

（四）异常孤立点、异常周期的检测

将已处理的数据用差于标准差的模型计算小区核心指标的相应倍数，求出以26019015、26019039、26019057小区的一段时间中小区内的平均用户数作为展示和分析。

若一段时间内只有一个异常点则为一个异常孤立点，在一天的时间周期中出现多个异常值则为异常周期。将除以2分别得到，的值。

可求出小区在异常点的总数， =1，2，3，…，58。=1，2，3。以一天为时间周期标准从00：00—23：00时间段中出现多个异常点属于异常周期，则异常周期的个数，见表2。

五、异常预测问题模型的建立与求解

（一）数据处理

根据58个小区提供的数据对所有指标进行相关性分析[2]，筛选出与小区内的平均用户数小区、平均激活用户、PDCP流量三个关键性指标相关性较强的指标因子。

三项关键性指标相关系数最高的指标数据，例如：平均激活用户数与最大激活用户数、空口上报全带宽 CQI为12的次数、MR 测量上报 RSRP 在 Index4 区间的次数的相关性都比原数据中其他指标数据较高，将三项关键性指标的相关系数较高的指标数据提取出来重复异常值步骤，为求解异常预测，做好数据处理。

（二）KPI异常值预测多元线性回归模型

多元线性回归分析是通过确定因变量与自变量，分析因变量与自变量之间关系的一种方法，进而确定变量间满足的方程[3]。本文将问题中所提供的数据进行划分，前500条数据作为训练数据，用于训练变量之间存在的关系，剩余数据用于测试数据训练的效果，关于小区平均用户数、平均激活用户、小区PDCP流量三个关键性指标的多元线性回归分析情况如下：

1.将平均激活用户数作为因变量，将上文中筛选出与平均激活用户数相关关系较强的指标作为自变量，使用EXCEL进行多元线性回归分析。

得到多元线性回归模型，如下：

1=0+11+22+33 （4）

其中， 0=0，1=0.45， 2=0.21，3=0.16。

2.将小区PDCP流量作为因变量，将上文中筛选出与小区PDCP流量相关关系较强的指标作为自变量，使用EXCEL进行多元线性回归分析。

可得到多元线性回归模型，如下：

2=0+1 1+2 2+3 3+4 4+5 5 （5）

其中，0=0，1=0.25，2=0.14，3=0.09，3=0.29，3=0.18。

3.将小区内的平均用户数作为因变量，将上文中筛选出与小区内的平均用户数相关关系较强的指标作为自变量，使用EXCEL进行多元线性回归分析。

可得到多元线性回归模型，如下：

3=0+11+22+…+1111+1212 （6）

其中，0=0.01，1=0.03，2=-0.08，3=0.01，4=-3.31，5=3.55，6=-0.30，7=-0.004，8=-0.02，9=0.10，10=0.01，11=0.07，12=0.93。

上述方程（4）、方程（5）、方程（6）可以实现对未来时段三个关键指标数据的变化趋势进行预测，以26019039小区的PDCP流量为例，将第500条之后的5个数据指标（UE缓存为空的最后一个TTI所传的上行PDCP吞吐量、扣除使UE缓存为空的最后一个TTI之后的上行数、平均激活用户数、最大激活用户数、MR测量上报RSRP在Index4区间的次数）代入方程（5），计算出预测值，现对指标预测情况与原始数据进行展示，如图1所示。

（三）预测评估指标模型

为检验构建的模型预测效果是否好，现构建预测评估指标模型对建立的KPI异常值预测多元线性回归模型的优劣进行判断。

以26019039号小区为例，分别计算小区内的平均用户数、平均激活用户数、小区总 PDCP 流量的F1值。

根据建立的多元线性回归模型，所求出的模型评估值 F1 得出该模型针对小区内的平均用户数指标预测效果较好，但平均激活用户数、小区总PDCP流量指标的预测效果明显欠佳，为此我们考虑再采用RBF神经网络模型进行求预测。

（四）KPI异常值预测RBF神经网络模型

RBF神经网络是将RBF高斯核函数应用于神经网络的一种模型，RBF神经网络通常只有三层，第一层是输入的各个指标原始数值，即输入层；中间的隐含层是多个高斯核函数，每个高斯核函数都以一个样本点或者一个聚类中心作为高斯核函数的参数。经过隐含层，数据相当于经过了非线性的变化；之后在第二层和第三层之间采用线性输出，利用线性加权的方法将隐含层的数据输出到输出层，作为最终的预测结果[4-5]。

将三个关键性指标作为因变量，对应三个关键指标相关性较高指标作为自变量[6-7]，构建RBF神经网络进行预测，将前200条预测结果与原始数据进行展示。

由于在异常判断时，数据的差与标准差的倍数得到的值采取了万分位四舍五入进行计算，为此使用RBF神经网络模型时会产生较小的偏差，为减小误差，本文作如下定义。

阀函数：当预测的指标数据与原始数据差的绝对值小于或等于0.05时，表示该预测的结果合理。

阀函数：                |- |≤0.05 （7）

其中，为原始数据，为预测数据，，=1，2....，n。

使用F1值对RBF 神经网络模型的优劣进行判断，通过使用RBF神经网络模型得到的F1值都在70%以上，将多元线性回归模型与RBF神经网络模型F1值的数据对比，见表3。

从表3可以看出，RBF神经网络模型的模型评估值F1值远优于多元线性回归模型，因此RBF神经网络模型更适合KPI指标的预测。

六、模型评价

KPI异常检测与异常预测是智能运维中最核心的问题。本文通过对数据进行特征分析，针对异常检测问题，提出了KPI异常值检测差与标准差模型，解决了寻找异常孤立点、异常周期问题；针对异常预测问题提出了KPI异常值预测多元线性回归模型、KPI异常值预测RBF神经网络模型，使用评价指标模型判断出两个模型的优劣，解决了异常预测问题。但智能运维中的异常检测无法完全避免故障的发生，只能通过提高系统的稳定性和可靠性，减少故障对系统的影响。因此，在智能运维中，需要不断地完善技术手段和提高算法的精度，采用多种方法相互协作，才能实现更精确、可靠的异常预测。

参考文献

[1]陈倩，戴跃伟，刘光杰.面向智能运维的KPI异常检测模型研究[J].重庆理工大学学报（自然科学），2022，36（06）：181-188.

[2]李军红，李付庆，范建民.统计学[M].南京：南京大学出版社，2020.

[3]陈佳佳.面向成分数据的回归分析研究[M].武汉大学出版社，202008.157.

[4]张泽旭.神经网络控制与MATLAB仿真[M].哈尔滨：哈尔滨工业大学出版社，2011.

[5]孙永谦，张茹茹，林子涵，等.KPI异常检测方法评估[J].数据与计算发展前沿，2022，4（03）：46-65.

[6]王速，卢华，汪硕，等.智能运维中KPI异常检测的研究进展[J].电信科学，2021，37（05）：42-51.

[7]张圣林，林潇霏，孙永谦，等.基于深度学习的无监督KPI异常检测[J].数据与计算发展前沿，2020，2（03）：87-100.