一种基于LM算法测量回转体内径方法

汪浩?冯志勇

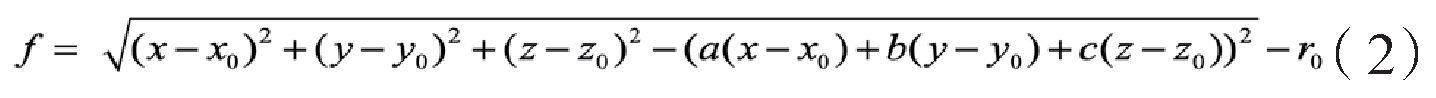
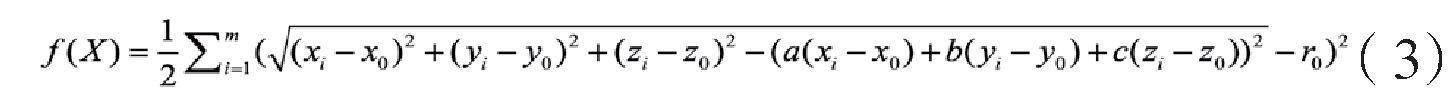
摘要：工业测量中测量回转体内径时，传统的接触式测量精度不够并且可能会损坏待测物，而采用三坐标测量机测量又面临着机器高昂的造价，针对以上问题提出了一种利用回转体检测仪配合轮廓仪使用收集待测物点云信息，并利用参数坐标转换将点云信息转换到直角坐标系中进行拟合，利用LM算法对圆柱面参数进行求解，进而得到回转体内径的方法。在MATLAB中对该方法进行仿真实验，实验结果也证明了该方法的可行性。

关键词：回转体内径；坐标转换；LM算法；圆柱面参数

一、前言

测量回转体内径是工业测量中比较常见的问题，回转体工件被广泛应用于农业、工业、国防等领域，随着现代加工和设计技术的不断进步，工业生产对回转体的测量精度及速度也提出了越来越高的要求。

回转体内径的测量方法包括接触式测量和非接触式测量。早期常见的接触式测量方法是利用外径千分尺或者游标卡尺等量具来测量，这些方法在读数时会有一定的误差。影像测量法也是常用的接触式测量方法之一，适用于测量外螺纹的中径、牙型角、牙距等参数，但是其对于检测螺纹中径等单一参数操作复杂，效率低，不利于大批量检测。随着三坐标测量机的出现，接触式检测迎来了飞速发展，天津大学的赵红岩等人研制出一台用于回转体零件内外表面测量的三坐标测量机，解决了螺纹作用中径自动测量的难题[1]。近些年，接触式检测内螺纹多参数已经取得了较大的进展，想要精确测得内螺纹的各项参数，接触式检测内螺纹一般需要通过精密的金属探头来扫描螺纹轮廓轴向截面上的点，通过获取的轮廓点云数据计算出螺纹工件的各项参数，虽然这种方法能够准确测量出螺纹的作用中径，但三坐标测量机的价格昂贵，测量的速率不高，并且接触式测量可能会对待测的零件有一定的磨损。因而非接触式测量回转体内径成为研究的热点。陆军工程大学的胡备等人提出了一种测量火炮内径的算法，该方法利用激光位移传感器和根据弦长计算直径的原理实现了火炮内径的非接触测量，但是其测量效率不高，不利于大批量炮管的检测。Zhang H等人利用CCD相机采集螺纹图像并处理图像得到点集信息，利用SVM对点集分类，通过数据分析得到螺纹参数[1]。Lee YC等人基于机器视觉开发了一套螺纹测量系统[2]。上海工程技术大学的刘瑞媛设计了一套回转体全外观视觉检测系统能够弥补回转体检测的缺陷[3]。机器视觉的检测方法虽然速度快，但是其检测结果的准确性依赖于成像的质量，因此这种方法的使用有一定的局限性。

针对以上回转体内径测量的问题，本文提出了一种非接触收集点云拟合圆柱面方法求回转体内径。这种方法在测量过程中无需接触待测回转体，故避免了对待测零件的磨损，使用的仪器相较于三坐标测量机也低廉很多，利用点云进行圆柱面拟合这种方法来求回转体的内径参数也避免了回转体倾斜放置对结果的影响，提高了精度，大大提高了测量的效率。

二、拟合原理

空间圆柱面是三维空间到定直线l的距离等于定长r的所有点组成空间几何图形为圆柱面，其中r为圆柱半径。根据上述圆柱面的几何定义，假设P点是圆柱上的任意一点，P0为该圆柱面轴线上的一点，坐标为（x0，y0，z0），（a，b，c）为该圆柱面轴线的向量，r0为该圆柱面的半径，则可以确定圆柱面的方程为：

（x-x0）2+（y-y0）2+（z-z0）2-[a（x-x0）+b（y-y0）+c（z-z0）]2=r02（1）[4]

根据（1）式构建算法模型：

由于该算法模型为非线性方程，只能通过非线性最小二乘法来求解未知参数。非线性最小二乘法主要有梯度下降法、牛顿法和LM法，三者都是以迭代的方式对参数进行求解，梯度下降法在距离极值点较远的时候收敛速度会较快，靠近极小值时收敛速度减慢，求解需要很多次的迭代，其贪心算法的本质可能会导致它的求解路径呈锯齿下降，无法求解。

牛顿法每一步计算都需要求解目标函数的海森矩阵，收敛速度快，但是计算过于复杂，且牛顿法是局部收敛的，因此对于初始值的选取有一定的要求，并且需要求解的海森矩阵必须可逆。高斯-牛顿法利用近似海森矩阵代替了海森矩阵，相比于牛顿法减小了计算量。但是近似海森矩阵要求是可逆且正定的，但实际计算中近似海森矩阵可能为奇异矩阵或者为病态的，如果步长过大甚至会导致不收敛，从而无法得到方程组的解。LM算法通过调节阻尼因子自适应调整达到收敛特性，减小近似海森矩阵的病态问题，兼顾了另外两种算法的优点，相比于梯度下降法，收敛速度要快很多，相比于牛顿法，LM算法拥有良好的鲁棒性，即使在初始值距离局部最优解非常远，也可以成功求解。所以在此选用LM算法进行拟合[5]。

首先，通过（2）式构建目标函数：

其中m是参数向量， 表示有效点的个数，为了减少后续迭代过程中可能出现奇异矩阵的情况，将收集到的圆柱面上的点进行重心化处理，处理公式如式（4）所示：

要使f（X）取得最小值，应满足f（X）的导数为0。

根据（4）式，可以求出雅可比行列式：

J（X）=F'（X）（6）

为了求解式（5）所示的非线性方程组，将其进行泰勒级数展开，通过对参数向量逐次迭代实现求解。设参数向量的初值X0，第k次迭代和第k+1次迭代后的值分别为Xk和Xk+1，令： Xk=Xk+1-Xk，

则有算式：

J（Xk）Xk=-F（Xk）（7）

引入阻尼因子 ，如式（8）所示：

[J（Xk）+μkI]Xk=-F（Xk）（8）

进而得到增量的计算公式如式（9）所示：

Xk=-[J（Xk）+μkI]-1F（Xk）（9）

由上式可以求得第 次迭代后的参数向量如式（10）所示：

Xk+1=Xk-[J（Xk）+μkI]-1F（Xk）（10）

设定收敛精度 0，若参数向量X满足精度要求，则有X*=Xk+1，并结束迭代过程。通过以上方法便能够得到圆柱面的参数X。

三、仿真实验

（一）实验装置

本次研究以实验室现有的激光位移传感器为核心器件构建了一套非接触式内螺纹检测设备。应用以直射式激光三角法测距的激光位移传感器作为非接触式扫描测针，通过PLC控制伺服电机，实现激光位移传感器的移动和转动控制，配合螺纹测量框架和夹具等附件，构建一套实现非接触检测内螺纹多参数的技术方案。

本次实验用到的实验装置是实验室经过改进的轮廓仪配合回转体检测仪来获取点云数据。该装置在激光位移传感器下方添加了一个反射镜，当轮廓仪无法进入到回转体内部扫描时，扫描激光通过该反射镜来实现回转体内部的扫描。实验装置图如图1所示。

（二）测量流程

此次仿真实验圆柱面拟合的具体流程主要分为以下几步：

1.利用实验室的回转体检测仪配合轮廓仪获取点云信息，获得的点云信息坐标记为（x，z），其中x表示轴上坐标值，z表示传感器发出激光到待测物的距离，为激光发出点到反射镜与反射镜到待测环规内壁的距离之和，将z值减去传感器到反射镜的距离R0，得到点云极坐标。首先需要对点云极坐标信息进行坐标转换，转换到直角坐标系中。

2.将收集的点云进行降噪处理有利于后续圆柱面拟合得到精确的圆柱面参数，因此首先对收集到的点云信息进行小波滤波降噪处理。一般情况下，小波分解的层数越多，去噪的效果就越好，但是，随着分解层数的增加，相应的计算量也会大大增加，为了保证工作效率，一般情况下，分解层数为3到5层。因此，在实验的时候分解层数选择了4层。小波去噪的基本问题分解成三个层面的问题：小波基的选择、阈值的选择和阈值函数的选择。对于阈值函数的选择，最常用的选择有硬阈值和软阈值。硬阈值函数可以很好地保留信号边缘等局部特征，软阈值方法相对比较平滑，但会造成边缘模糊等失真现象，传统的阈值函数不具备高阶可导性。我们使用改进的半软阈值函数进行降噪处理。改进的半软阈值函数如式11所示：

目前常见的阈值选择有固定阈值、启发式阈值、无偏似然估计阈值和极值阈值，阈值的选择不同，小波滤波去噪的效果也有所差异。对此，我们对不同的小波基以及阈值进行实验，最终发现haar小波和固定阈值时，均方根误差最小，小波滤波的效果最好。

3.确定出圆柱面拟合的初始值，该圆柱面拟合算法有着至关重要的作用，一般来说，初值越接近实际值，收敛得越快。圆柱面拟合的7个参数中，x0，y0，z0是相关的，a，b，c也是相关的，故为了保证起始点的坐标以及轴向量具有唯一性，我们需要对其添加一些约束关系，约定方向向量为单位向量且指向正方向，对此，我们可以得到下面的条件方程：a2+b2+c2=1[6]；根据以往经验，在此次拟合算法中，我们可以取a=0，b=0，c=1；由于实验中的环规都是正放在仪器，故其圆柱面均可认为是正圆柱，因此，我们可以任取轴上一点确定x0，y0，z0，r0取所有轮廓点的z值的平均值，以上本次拟合圆柱面算法的初值都已确定。

4.在MATLAB上进行仿真实验，利用上述LM算法求解圆柱面参数。MATLAB中的多元非线性回归函数便是利用了LM算法对参数进行求解，求解方程如式12所示：

beta=nlinfit（X，Y，modelfun，eta0，options）（12）

其中modelfun为拟合指定模型，即为（3）式，X，Y为预测变量和响应值，此处X即为点云信息转换在直角坐标系的坐标值构成的xyz数组，Y初始化为长度为轮廓点数量，值均为0的一维数组，实验中记为zeroes（count，0），count为点的数量，beta为此次拟合参数的初始值，实验中记作P0，options为指定的评估算法，实验中创建一个opts对象，并将其允许迭代的最大次数设为2000，即beta为此次多元非线性回归后得到的圆柱面的参数值，记为P，将上述参数代入多元非线性回归函数中，得到本次圆柱面拟合的参数P，进而得到待测环规的内径。

（三）仿真结果

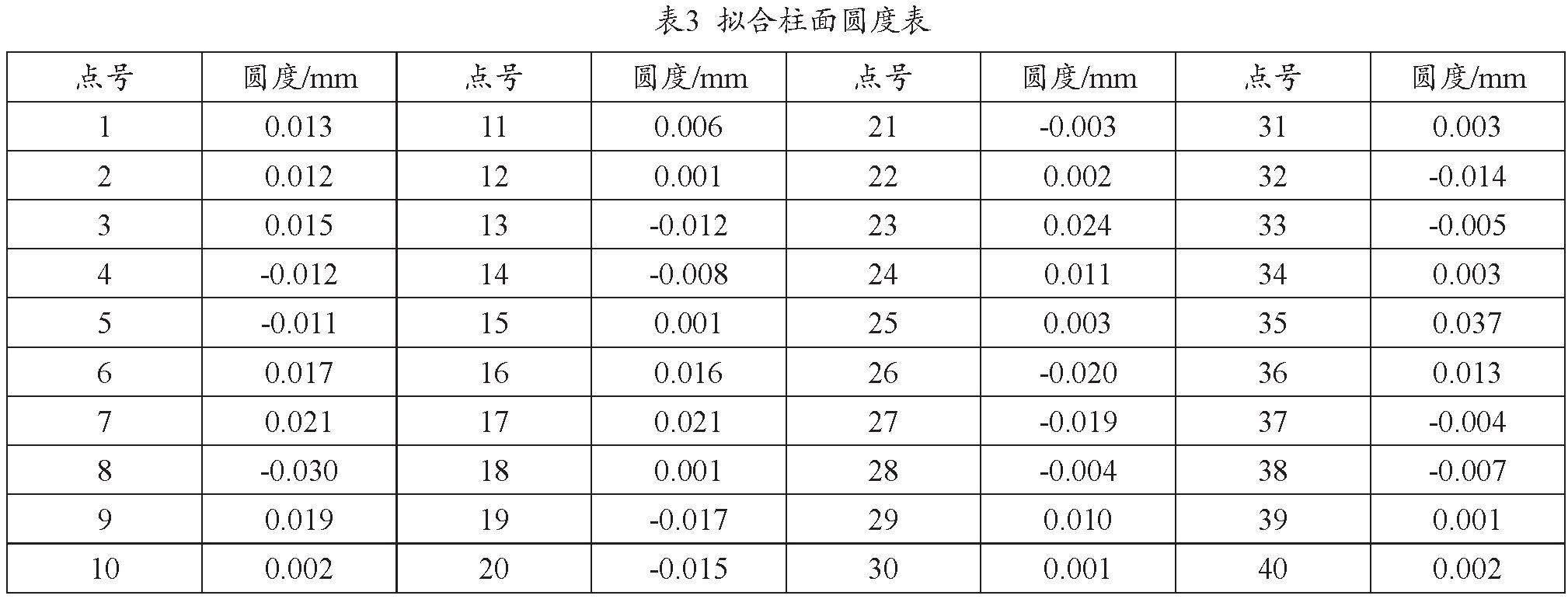
利用系统点云采集装置对待测环规进行扫描，由伺服电机带动轮廓仪旋转一周，收集待测环规270条轮廓的点云信息，利用上文提到的基于LM算法的圆柱面拟合算法模型进行拟合，得出数据拟合的圆柱面的圆柱轴线的初始点（x0，y0，z0），圆柱面的轴线向量（a，b，c），圆柱面的半径r0这7个参数如表 1所示。在MATLAB中画出由上述圆柱面方程确定的唯一圆柱面，如图2所示。绿色为原始点云数据，整个圆柱面为原始点云数据拟合的圆柱面。通过上述数据易得该环规的内径为60.0044。继续用另外两组点云数据进行上述实验，三次检测结果与环规内径相比较的结果如表 2所示。圆度是评价一个圆柱面拟合算法有效与否的重要参数，其定义为圆柱面表面上的点到圆柱中轴线的距离与圆柱面半径之差。在此列出一条轮廓上的部分牙型上的点的圆度值，如表 3所示。根据表3对R进行统计分析，R的均值等于零，R的标准差为0.33mm，准确性很高。根据上述实验结果可知，拟合柱面圆度准确性很高，测得的环规内径结果均在实验误差的允许范围值内，因此用基于LM算法的点云拟合柱面来求回转体内径的算法是可行的。

四、结语

本文介绍了一种利用LM算法来实现求解拟合圆柱面的参数进而得到待测环规内径的方法，并在MATLAB上进行仿真实验，最终画出了该算法求解的参数所确定的圆柱面，并通过圆柱面参数求解了该环规的内径，证明了该算法的可行性。该方法测量回转体内径需要对点云信息进行野值剔除，准确的点云信息对后续的拟合准确度有着至关重要的影响，因此后续的优化可以从点云信息的野值剔除算法进行改进，提高测量回转体内径的精度。与传统的测量回转体的方法相比，这种方法避免了与回转体的直接接触，实现了非接触式自动检测，并且通过实验结果证明了该方法测量的环规内径结果精确度也很高，利用反射镜配合线激光轮廓仪不仅大大提高了收集点云信息的效率，对测量较小的回转体也有很好的实用性，扩大了该方法测量回转体的使用范围，从而大大提高了测量的效率，所以该方法测量回转体内径在工业测量中具有很高的实用价值。

参考文献

[1]ZHANG H，JIN G，JIANG Y，et al. External screw thread parameters detection by machine vision based on SVM feature point classification[J]. Transducer and Microsystem Technologies， 2019.

[2]LEE Y C，YEH S S.Using Machine vision to develop an on-machine thread measurement system for computer numerical control lathe machines[C]//Lecture Notes in Engineering and Computer Science： Proceedings of The International MultiConference of Engineers and Computer Scientists. 2019： 13-15.

[3]刘瑞媛.回转体零件全外观视觉检测系统设计与实现[D].上海：上海工程技术大学，2020.

[4]袁建刚，潘轶.一种圆柱面拟合方法[J].工程勘察，2017，45（12）：60-64.

[5]周小宁，王立权，朱伟华，等.基于LM算法的近似核FFT频率拟合算法[J].舰船电子对抗，2020，43（05）：44-49.

[6]申旭，朱文芳，王伟峰，等.一种空间圆柱面拟合计算方法[J].测绘科学技术学报，2018，35（06）：601-604.